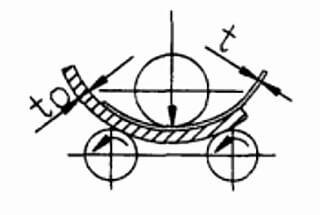
기계에서 롤러 사이의 중심 거리를 계산하는 데 어려움을 겪은 적이 있나요? 이 블로그 게시물에서는 이 중요한 측정값을 결정하는 간단한 방법을 살펴봅니다. 전문 기계 엔지니어가 귀중한 인사이트와 실용적인 예시를 제공하며 프로세스를 안내합니다. 이 과정을 마치면 이 일반적인 문제를 해결하고 기계 설계 기술을 향상시키는 방법을 명확하게 이해할 수 있을 것입니다.
보일러 및 압력 용기 제조에서 성형 기술은 주요 제조 공정 중 하나입니다.
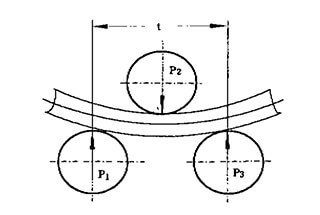
성형 공정에서 실린더 섹션의 롤링은 가장 기본적인 성형 방법입니다. 압연에는 많은 작업이 수반됩니다. 대부분의 성형 공정은 대칭형 3롤 벤딩 머신에서 수행됩니다. 하지만 생산 공정 조건에 따라 실린더 섹션의 두께와 직경이 결정되기 때문에 사양과 종류가 상당히 다양합니다.
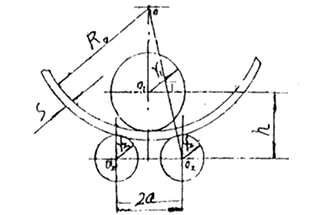
성형 후 곡률의 정확도는 롤링이 끝날 때 상부 롤러와 하부 롤러 사이의 중심 거리인 파라미터 'H'에 따라 달라집니다.
이 매개변수는 일반적으로 공식 (1)에 의해 결정됩니다.
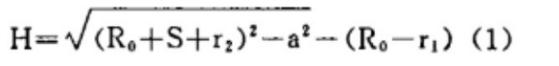
이 공식은 복잡하지 않은 것처럼 보일 수 있지만 제조업체의 경우 실린더 섹션의 다양한 사양과 종류로 인해 누적 작업량이 상당합니다.
다양한 조건에서 'H'의 값을 단순화하고 쉽게 결정하기 위해 이 글에서는 다음 두 가지 그래픽 알고리즘을 사용합니다.
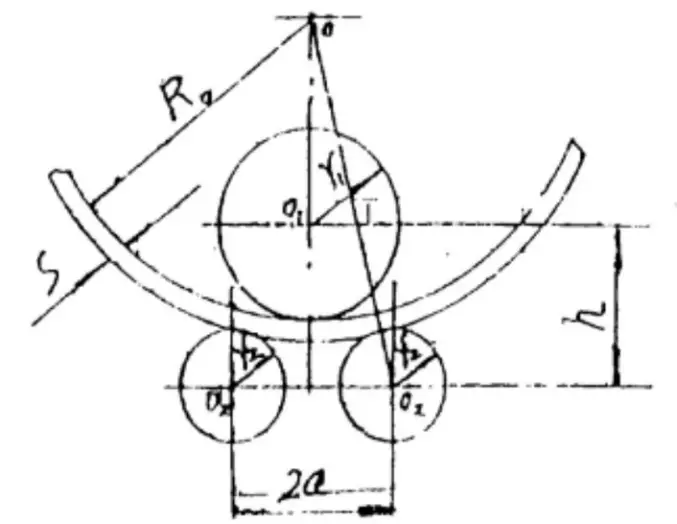
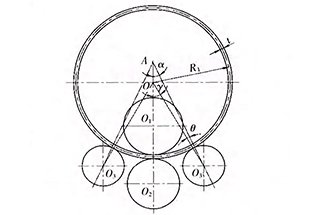
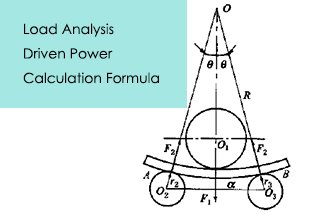
그림 1 대칭형 3 롤러의 끝 위치 다이어그램 플레이트 벤딩 머신
특정 유형의 플레이트 압연기 가 주어지면 매개변수 a, r1 및 r2 는 상수이며, 위 공식에서 s와 R0 는 변수입니다.
따라서 특정 유형의 플레이트 벤딩 머신 를 사용하여 두께와 곡률 반경을 굴리면 다음 그래프 알고리즘을 통해 해당 주요 매개변수 'h'를 얻을 수 있습니다.
먼저, 직사각형 좌표계가 설정되고 a를 좌표좌표로, h를 종축좌표로 사용합니다.
그런 다음 좌표계에서 다음 그림이 수행됩니다 (그림 2 참조).
세로축에서 OP = a를 가로채고, 점 P를 원의 중심으로 삼고, (R0 + S + r2)를 반경으로 하여 호 교집합의 가로축에 양의 점 a를 만듭니다.
점 a를 원의 중심으로 삼고, R을 취해야 합니다.0 를 반지름으로, 그 반대를 호의 가로축에 있는 점 B로 지정합니다.
그런 다음 점 B를 원의 중심으로 삼고 R1 를 호 교집합의 반지름으로 삼고 호의 가로축 양의 방향에 점 C를 만듭니다.
따라서: OC = h.
예를 들어
S = 20mm, d = 2,000mm의 드럼 섹션은 70 × 4000 대칭 3롤 플레이트 벤딩 머신에서 압연됩니다.
h의 값을 계산하려면
데이터에 따르면, R1 = 350mm, R2 = 330mm, 2a = 800mm.
그래프 알고리즘(그림 2 참조)에 따르면 h = 640mm이며, 이는 공식에 의해 계산됩니다:
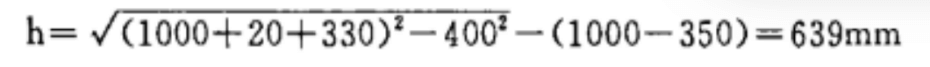
절대 오차는 1mm에 불과하며 실제 값의 0.015%를 차지하므로 충분히 정확합니다.
(R + S + r)을 움직이는 눈금자로 만들면 더 편리합니다.
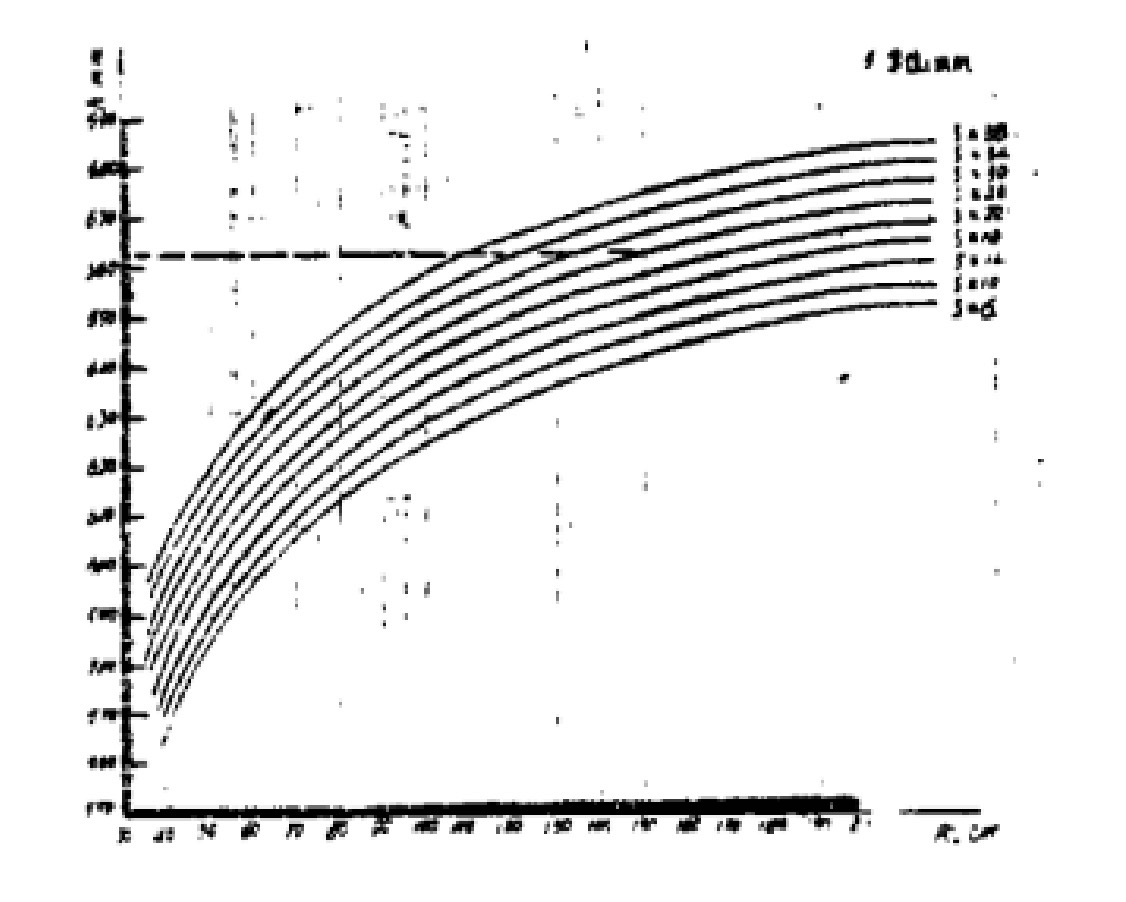
그림 2 "h"를 계산하는 노모그램
위에서 알 수 있듯이 특정 굽힘 유형 기계가 주어지면, 그 매개변수 a, R1 및 R2 는 고정되어 있습니다.
그런 다음 R의 관계 곡선이0 로, 다른 판 두께 아래의 h는 r로 그려집니다.0-h 좌표계, R의 공통점 그래프0 이 유형의 두께가 다른 강판의 두께는 롤링 머신 를 얻을 수 있습니다.
모든 다른 조건에서 이러한 유형의 플레이트 벤딩 머신에서 드럼 섹션의 주요 매개 변수 "h"의 값을 얻는 것이 매우 편리합니다.
다음은 70 × 4000 대칭 삼각형의 공통점 다이어그램입니다. 롤러 플레이트 벤딩 머신.
알려진: r1 = 350mm, r2 = 330mm, a = 400mm
그래서:
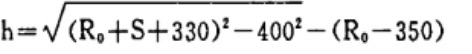
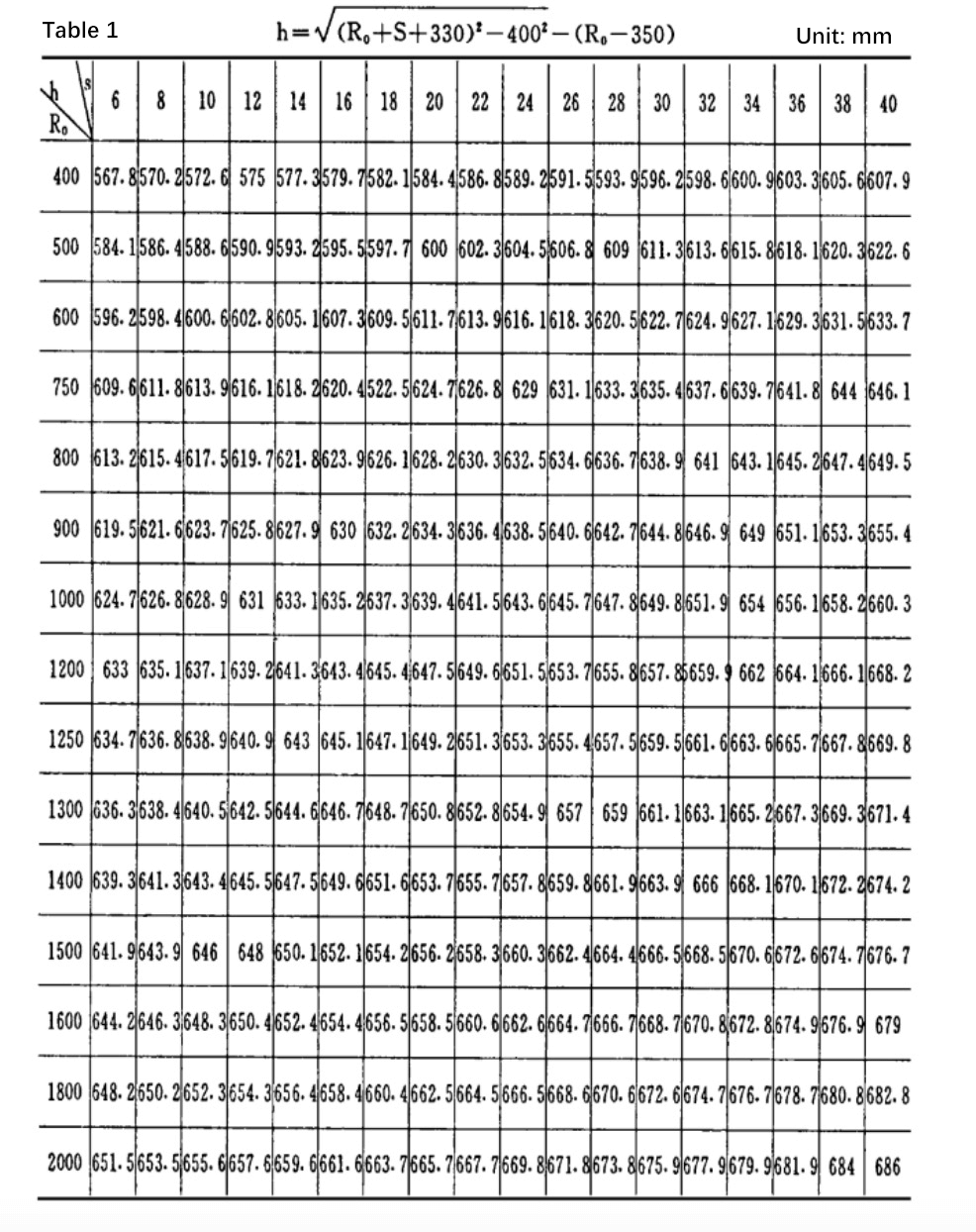
표 1은 2mm 간격의 계산 및 도면 데이터 표입니다.
실제 경험에 따르면 롤링 머신 는 일반적으로 6 ≤ s ≤ 40(mm)입니다.
일반적으로 롤링 드럼 섹션의 반경은 400 ≤ R입니다.0 ≤ 200(mm).
따라서 이 범위가 계산 도면 범위로 사용됩니다.
표 1에서 특정 유형의 플레이트 벤딩 머신을 사용하여 일정량의 R을 압연할 때 "n"의 값은 기본적으로 플레이트 두께 s와 동일하다는 것을 알 수 있습니다.0.
실제 값과 실제 값 사이의 오차는 0.05% 미만입니다.
그러나 동판이 구부러지면 소성 변형과 탄성 변형이 모두 발생합니다.
따라서 언로드 후 어느 정도 탄력적인 회복이 있을 것입니다.
따라서 실제 생산에서는 이 값이 실제 값보다 약간 적어야 합니다.
이런 식으로 두 가지의 등가 변화의 법칙을 사용하면 그림이 단순화되고 탄성이 있습니다. 스프링백 실제 구부러진 후 보정할 수 있습니다.
동시에 그래프 선을 줄일 수 있으며, 특정 R 아래에서 모든 S에 해당하는 "h" 값을 결정할 수 있습니다.0.
전자의 그래프 알고리즘은 보편적인 반면 후자는 특정 유형의 플레이트 벤딩 머신에 대한 것으로, 어떤 유형의 플레이트 벤딩 머신이 특수(k-R0-S) 복사점 그래프.
두 가지 그래프 알고리즘의 교육 결과는 매우 훌륭하고 학생들에게 큰 깨달음을 줍니다.
특히 후자의 방법은 어느 정도 실용성이 있습니다.
플레이트 벤딩 머신 제조업체는 (n-R)의 공통 주 다이어그램을 구성하는 것이 좋습니다.0-S)의 롤링 머신 또는 매뉴얼에서 확인할 수 있으며, 이는 제조업체의 실제 생산에 큰 편의를 가져다 줄 것입니다.