Berekening van de lagerlevensduur: De geheimen van het voorspellen van de lagerlevensduur

Praktische berekening van lagerlevensduur

Eerder hebben we besproken hoe je de levensduur van een lager berekent. In die artikelen introduceerden we vooral de theoretische aspecten van de levensduur van lagers en de berekeningsformule.

Vandaag willen we die theorie toepassen op praktische scenario's. Het uiteindelijke doel van het verwerven van theoretische kennis is immers om praktische engineeringbehoeften te dienen. Sommige ingenieurs hebben gevraagd om rekenvoorbeelden uit de praktijk, dus laten we dieper ingaan op het voorbeeld uit ons vorige artikel.

Laten we het voorbeeld van de verticale motor nog eens bekijken. Hier zijn de relevante lagergegevens:

• Lager model: 6208
• Dynamische basisbelasting van het lager: 29kN
• Equivalente dynamische belasting van het lager: P=5,83kN

Laten we ook wat extra parameters opgeven voor deze lager:
Lagersnelheid: n=1500rpm

Met behulp van de formule voor de lagerlevensduur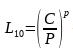verkrijgen we de levensduur van het lager:

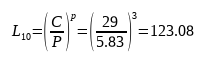
Hier is p de berekeningscoëfficiënt voor het lager. Als het wentellagerelement een kogel is, is p 3 en als het wentellagerelement een rol is, is p 10/3. De resulterende levensduur van het lager is 123,08, in miljoen omwentelingen. Omgerekend naar een meer gebruikelijke tijdseenheid krijgen we:

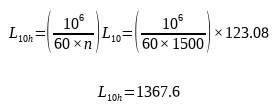
De berekende levensduur van het lager is ongeveer 1368 uur.

In dit voorbeeld hebben we een scenario gebruikt waarbij het lager zwaar wordt belast. Het berekende resultaat suggereert dat het lager niet geschikt is voor deze toepassing vanwege de korte levensduur. Als de motor continu draait, kan de nominale basislevensduur slechts zorgen voor minder dan twee maanden lagerwerking.

Dat wil zeggen, als we dit lager kiezen, kunnen we alleen garanderen dat 90% van de lagers continu kan werken gedurende twee maanden onder deze omstandigheden.

Het bovenstaande is de levensduur van het lager die wordt verkregen met behulp van de basistheorie over de levensduur van het lager.

Maar zoals je misschien hebt gemerkt, net als in onze vorige artikelen, houdt het hele berekeningsproces alleen rekening met de belasting op het lager. Met andere woorden, deze zogenaamde nominale levensduur van het lager houdt alleen rekening met de impact van de belasting. Zoals we in onze vorige artikelen hebben besproken, voldoet deze berekening na vele jaren van ontwikkeling in de moderne lagerlevensduurtheorie niet meer aan onze behoeften. Daarom moeten we deze waarde verder aanpassen.

Dat wil zeggen, we moeten de gewijzigde levensduurwaarde van het lager berekenen. De meeste van de daaropvolgende berekeningen maken geen gebruik van formulemethoden omdat deze berekeningen complex kunnen zijn, veel van de processen of referentietheorieën komen van experimenten, en ten derde hebben verschillende lagerleveranciers en internationale lagerstandaarden ons een beter referentiehulpmiddel gegeven - grafieken. Hoe gebruiken we deze grafieken? Laten we dit onderzoeken aan de hand van ons voorbeeld.

Aangepaste nominale levensduur van lagers

Zoals beschreven in onze vorige artikelen is de formule voor de aangepaste levensduur als volgt:

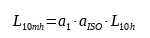
Om de uiteindelijke waarde L_10mh moeten we a1 en a_iso.

01 Eerst definiëren we a1.

Zoals we eerder hebben besproken, staat a1 bekend als de betrouwbaarheidscoëfficiënt van de aangepaste levensduur. Wanneer de betrouwbaarheid 90% is, is de waarde van a1 1. Voor machines voor algemeen gebruik die in de industrie worden gebruikt, is de levensduur van het lager altijd gebaseerd op een betrouwbaarheid van 90%, tenzij dit specifiek vereist is. Daarom kunnen we in dit voorbeeld direct a1 nemen.

02 Ten tweede vinden we een_iso.

De standaardmethode voor het berekenen van de aangepaste levensduurcoëfficiënt a_iso van een lager houdt rekening met de volgende factoren:

• Lagerbelasting
• Smeeromstandigheden (type en viscositeit van het smeermiddel, snelheid, grootte van het lager, of er additieven zijn gebruikt)
• Vermoeiingsgrens van het lager
• Type lager
• Restspanning van het lager
• Milieuomstandigheden
• Verontreiniging in het smeermiddel

Samengevat_iso is een functie van de volgende parameters:

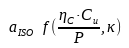
Waar:

• η_c is de vervuilingsfactor van het lager,
• C_u is de vermoeiingsgrens van het lager,
• k is de viscositeitsverhouding van het lagersmeermiddel.

Eerst selecteren we de vervuilingsfactor ηc van het lager. In de ISO281-norm en alle lagerfabrikant catalogi is er een referentietabel voor selectiecriteria:

In de toepassing van verticale motoren, gebaseerd op onze eerdere ervaring, moet de vervuilingsfactor voor lagers worden gekozen tussen lichtvervuiling en algemene reinheid. In dit geval kiezen we een vervuilingsfactor van 0,6, wat iets hoger is dan algemene reinheid.

Laat me toevoegen,

Voor de selectie van de vervuilingsfactor is er geen specifieke wiskundige formule. Het is over het algemeen gebaseerd op jaren van dragende toepassing ervaring. Hoe meer toepassingen we tegenkomen, hoe meer inzichten we krijgen in deze selectie.

Aangezien het gekozen lager 6208 is, is de grenswaarde voor vermoeiingsbelasting C_u van dit lager kan worden gevonden in de lagercatalogus als: 1,05kN

De equivalente dynamische belastingswaarde van het lager werd in het vorige hoofdstuk berekend als P=5,83kN

Daarom kunnen we een benaderende waarde krijgen:

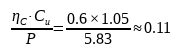
Vervolgens moeten we een iets complexere keuze maken voor de viscositeitsverhouding k. Vanwege de beperkte ruimte in dit hoofdstuk zullen we niet ingaan op de specifieke betekenis van k en hoe we deze waarde moeten kiezen. We zullen hier later in een ander artikel dieper op ingaan. Voor nu willen we alleen benadrukken dat het voor lagers heel belangrijk is om de juiste smering te kiezen. Dit heeft niet alleen te maken met de kwaliteit van het vet zelf, maar ook met de invloed van de smering op de lagers.

Wat betreft de viscositeitsverhouding,

In het algemeen hopen we dat de uiteindelijk gekozen smeerwaarde van k kan worden gekozen tussen 1 en 4, met verschillende overwegingen.

Als de berekende k-waarde van de geselecteerde smeerwaarde is:

• Minder dan 1 betekent dat de smering niet het gewenste effect heeft bereikt. Het doel van een smeermiddel is om het staal-op-staalcontact tussen de lagerloopbaan en het wentellichaam te scheiden. Als k<1 is, betekent dit dat het smeermiddel het staal-op-staalcontact niet heeft gescheiden en dat het lager nog steeds wrijving zal genereren als het draait.
• Groter dan 4 betekent dat er te veel smeermiddel is toegevoegd. Hoewel dit het metaalcontact perfect scheidt, zal het teveel aan smeermiddel in het lager een koppel genereren die we "weerstandsverlies" noemen. Dit is een zeer belangrijk onderdeel van het lagerwrijvingsmodel. In lekentaal: het belangrijkste doel van smering is om de wrijving te verminderen en de temperatuur van het lager verder te verlagen. Te veel smeermiddel kan echter ook "wrijving" opwekken, waardoor ook warmte wordt opgewekt.

Daarom hebben we een geschikte smeerwaarde gekozen en de uiteindelijke k-waarde is 1,5.

Met deze twee parameters kunnen we de volgende grafiek vinden in ISO281 of in de catalogus van de lagerfabrikant.

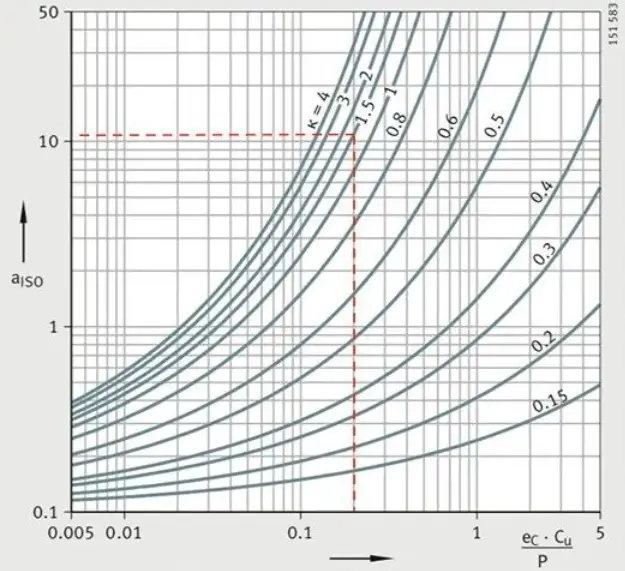
Let op!

Er zijn verschillende vergelijkbare diagrammen, elk voor verschillende soorten lagers. Wij hebben gekozen voor diepgroefkogellagers, een type radiale kogellagers. Selecteer daarom het juiste diagram op basis van het specifieke lagertype.

Uit het gekozen diagram kunnen we afleiden dat, onder deze toepassing, aiso=12.

In dit voorbeeld is de uiteindelijke gecorrigeerde nominale levensduur van lager 6208:

L_10mh = a₁×a_iso×L_10h = 1×12×1367.6 = 16411.2

In deze verticale motor kan het lager, bij de juiste smering, uiteindelijk 16.410 uur werken.

Doel van de berekening

Aangezien het resultaat van de berekening van de lagerlevensduur de werkelijke levensduur van het lager niet nauwkeurig kan weergeven, wat is dan het doel van deze berekening?

Veel ingenieurs vatten levensduurberekening zelfs verkeerd op als "waarzeggerij", waarschijnlijk vanwege de naam. Oorspronkelijk was het doel van het bestuderen van de vermoeiingslevensduur van lagers het vaststellen van een referentiewaarde, een levensduurreferentie. Na verloop van tijd is deze referentiewaarde een parameter geworden voor het vergelijken en verifiëren van de redelijkheid van lagerselectie.

In feite is de berekening van de levensduur van een lager een controle van de belastbaarheid van het gekozen lager. Met andere woorden, het gaat erom het kleinste lager te kiezen dat aan de levensduurvereiste kan voldoen. In die zin is de berekening van de levensduur van het lager een vereiste voor de ondergrens van het draagvermogen van het lager.

Hoe kunnen we dit begrijpen? Laten we beginnen bij het proces van levenscontrole:

Wanneer ingenieurs de levensduur van lagers controleren, geven handleidingen voor mechanisch ontwerp en materiaal voor apparatuur altijd een aantal minimumwaarden voor de levensduurvereisten. Het volgende is een voorbeeld:

Sommige fabrikanten van apparatuur stellen andere eisen aan de levensduur. Vaak wordt aan deze levensduurwaarden voldaan door de lagers in traditionele ontwerpen.

Bij het ontwerpen van nieuwe apparatuur en het controleren van de levensduur van de lagers kan dus de volgende aanpak worden gebruikt:

• Als de levensduur van het nieuw gekozen lager korter is dan de vereiste levensduur: Het draagvermogen (en de bijbehorende levensduur onder deze belasting) van het gekozen lager is lager dan dat van de lagers die eerder aan deze voorwaarde voldeden. Met andere woorden, het gekozen lager is te klein;
• Als de berekende levensduur van het nieuw gekozen lager groter is dan of gelijk is aan de vereiste levensduur: Het draagvermogen (en de bijbehorende levensduur onder deze belasting) van het gekozen lager is groter dan dat van de lagers die eerder aan deze voorwaarde voldeden. Met andere woorden, het gekozen lager is te groot;

Een te kleine of te grote keuze zou binnen een redelijke marge moeten liggen en absolute gelijkheid zou niet nagestreefd moeten worden. Daarom zal men bij het observeren van de "vereiste levensduur" merken dat deze waarde een bereik is, geen absolute waarde.

Daarom impliceert de impliciete berekening van de lagerlevensduur het controleren van de laadcapaciteit van het lager onder redelijke levensduurvereisten. Met andere woorden, kies een lager van redelijke grootte onder gegeven werkomstandigheden.

In het echte leven komen door misverstanden over de bovenstaande concepten veel "verkeerde operaties" voor:

(1) De berekende levensduur van een lager moet overeenkomen met de garantieperiode van de apparatuur.

Deze praktijk verwart de controle van de lagerbelasting met de levensduur van de apparatuur. In feite is de controle van de levensduur van een lager niet gelijk aan "waarzeggerij", zoals uitgelegd in het vorige artikel.

De werkelijke lageromstandigheden variëren en ingenieurs kunnen niet elke machine afzonderlijk berekenen. Dit is een misverstand bij machinefabrikanten over de "berekening van de levensduur van lagers".

Het concept van een garantieperiode legt alle verantwoordelijkheid bij de fabrikant van de apparatuur, een "garantie"-concept dat veel breder is dan het concept dat wordt gedekt door de "berekening van de levensduur van lagers", waardoor een dergelijke directe toepassing ongepast is.

Natuurlijk worden sommige ingenieurs onder druk van de klant gedwongen om te voldoen aan de eis van een "20-jarige" levensduur. Onder een dergelijk mandaat worden de gekozen lagers vaak overgedimensioneerd, wat niet alleen tot economische inefficiëntie leidt, maar ook miskent dat grotere of langere levensduurberekeningen niet altijd beter zijn voor lagers.

(2) Hoe langer de berekende levensduur van een lager, hoe beter het klinkt.

In feite is dit ook misleidend voor de keuze van lagers. Zoals ik al eerder zei, is de levensduurcontrole een controle van de minimale belastbaarheid van lagers onder werkomstandigheden.

Aan de andere kant moet er ook een limiet zijn voor het maximale draagvermogen van lagers, wat de bovengrens is van het draagvermogen van lagers onder werkomstandigheden. Als het berekeningsresultaat deze waarde overschrijdt, zullen er problemen optreden met het lager.

Dit is wat we vaak de "minimale belasting van het lager" noemen. Als het gekozen lager te groot is en de berekende levensduur van het lager onder werkomstandigheden lang is, wat betekent dat de belastbaarheid van het lager erg hoog is, voldoet het mogelijk niet aan de minimale belastingseis van het lager.

Als de belasting die door het lager wordt gedragen lager is dan de vereiste minimale belasting, kunnen problemen zoals rollende elementen slip optreden in het lager, waardoor het meer vatbaar voor doorbranden.

Inzicht in het concept van lagerlevensduur kan leiden tot talloze optimalisaties in het ontwerp. Deze omvatten:

Beoordelen of het mogelijk is om het lager kleiner te maken en toch aan de levensduurvereisten te voldoen;

De levensduur van een groot aantal lagers bijhouden en verdere verkleining overwegen als er nog enige restlevensduur overblijft.

Samengevat, in de technische praktijk wordt de berekening van de lagerlevensduur gebruikt om de belastbaarheid van het lager te verifiëren, niet om het gewoon te maximaliseren. Bovendien weerspiegelt de berekende levensduur niet de "echte" levensduur van het lager.

Een nauwkeurig begrip van de levensduur van lagers helpt bij de juiste selectie van lagerafmetingen.

Helaas moeten we in ons werk soms voldoen aan de eisen van onze klanten, zelfs als we denken dat hun verzoeken technisch onredelijk zijn. Voel je daarom vrij om dit artikel met hen te delen.

Dit is misschien wel het meest uitdagende artikel om te begrijpen op de website tot nu toe, vooral voor elektrotechnici. Als iemand vragen heeft, laat dan gerust een reactie achter voor discussie.