
Heb je je ooit afgevraagd hoe je de buigtoeslag voor je metaalbewerkingsprojecten precies berekent? In deze blogpost verkennen we de fascinerende wereld van formules en berekeningen voor buigtoeslag. Als ervaren werktuigbouwkundig ingenieur leid ik je door de belangrijkste concepten en geef ik je praktische inzichten om je te helpen dit cruciale aspect van het ontwerpen van plaatwerk onder de knie te krijgen. Bereid je voor op een duik in de wereld en ontdek de geheimen van nauwkeurige en efficiënte bochten in je projecten!

Toeslag voor buigen is een essentieel begrip op het gebied van plaatbewerking, vooral bij buigbewerkingen. Het verwijst naar de extra lengte materiaal die nodig is om de buiging in de metalen plaat op te vangen. Het begrijpen en nauwkeurig berekenen van de buigtoeslag is essentieel om ervoor te zorgen dat de uiteindelijke afmetingen van het gebogen onderdeel voldoen aan de ontwerpspecificaties.
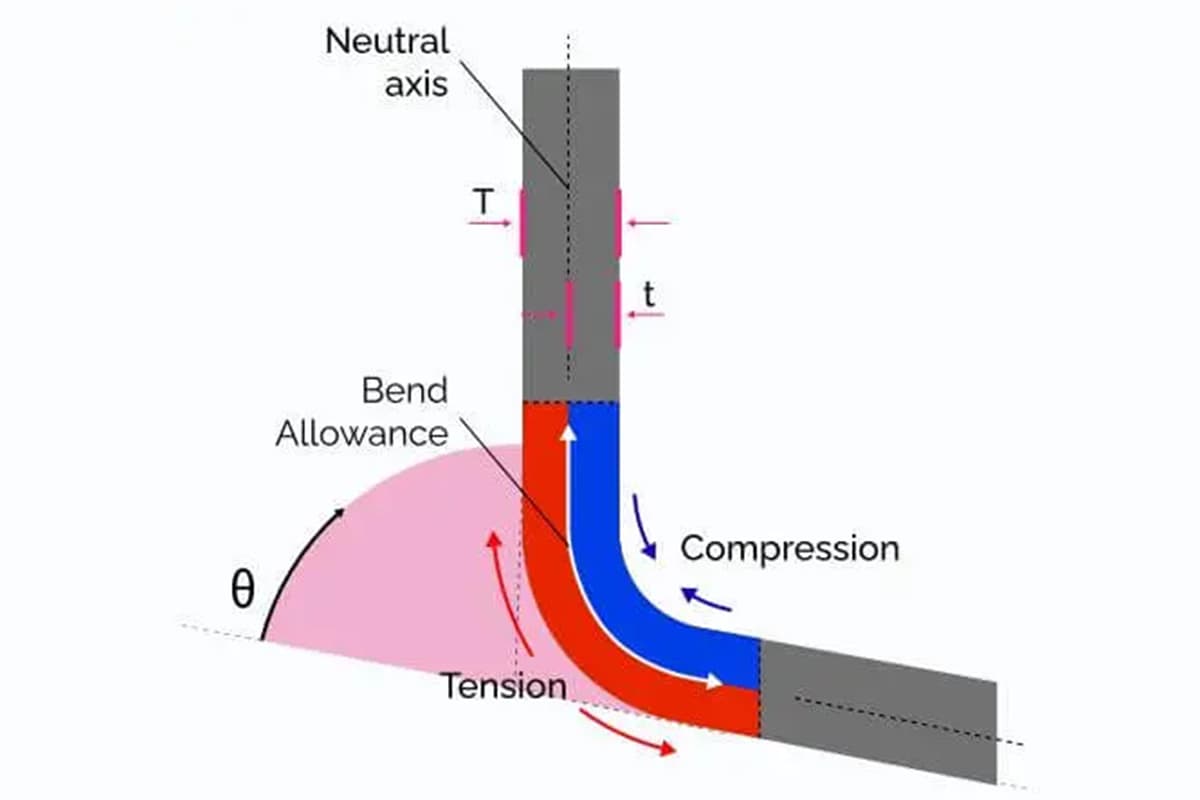
Nauwkeurige berekeningen van buigtoeslagen zijn van vitaal belang in het fabricageproces. Wanneer een vlakke plaat metaal wordt gebogen, rekt het materiaal aan de buitenkant van de bocht uit, terwijl het materiaal aan de binnenkant wordt samengedrukt. Zonder rekening te houden met deze vervorming zou het eindproduct niet overeenkomen met het bedoelde ontwerp, wat leidt tot onnauwkeurigheden en mogelijke mislukkingen. Buigtoeslag helpt fabrikanten om de afmetingen van het vlakke patroon aan te passen, zodat het gebogen onderdeel precies aan de vereisten voldoet.
Verschillende kritische parameters beïnvloeden de berekening van de buigtoeslag:
Het concept van Buigtoeslag is als volgt: wanneer een metaalplaat gebogen wordt, heeft deze drie dimensies - twee buitenmaten (L1 en L2) en een dikte (T).
Het is belangrijk op te merken dat de som van L1 en L2 groter is dan de uitgevouwen lengte (L) en het verschil tussen de twee staat bekend als de buigtoeslag (K).
De uitgevouwen lengte van een bocht kan dus worden berekend als L = L1 + L2 - K.
Gerelateerde lectuur:
Hoe was de formule voor Buigtoelage gemaakt? En hoe bereken je Buigtoelage?
De buigtoeslag is afhankelijk van de gevormde binnenradius. De onderste V matrijsopening bepaalt de binnenradius (I.R.) van een gevormd onderdeel. De binnenradius voor zacht staal is 5/32 x de onderste V matrijsopening (W) als de ponsradius kleiner is dan 5/32 x W.
Als I.R.< materiaaldikte (t)
Als I.R.> 2 x materiaaldikte (t)
Waarbij A= (180 - Krommingshoek inbegrepen)
Als de binnenstraal gelijk is aan t of 2t, of tussen t en 2t ligt, wordt de buigtoeslag berekend door de waarden van de buigtoeslag uit de twee bovenstaande formules te interpoleren.
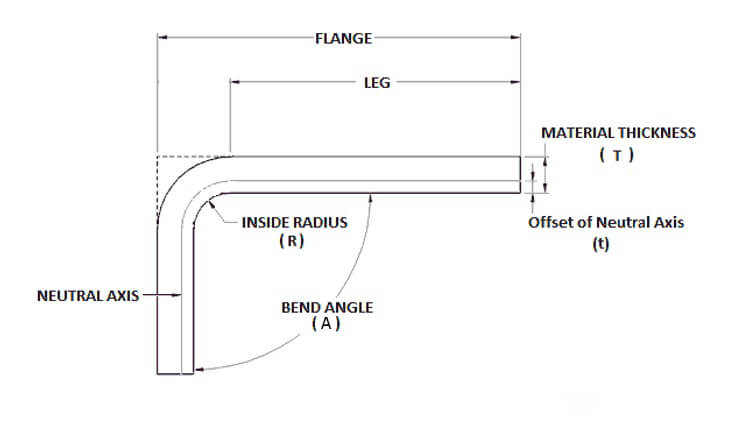
Om deze buigtoeslag te berekenen, kun je ook de volgende formule gebruiken:
Deze formule houdt rekening met de verschillende geometrieën en eigenschappen van de te vormen onderdelen.
De materiaaldikte (T), buighoek (A), binnenste buigradius (R) en de K-factor van het te buigen materiaal zijn de meest kritische factoren in deze berekening.
Zoals duidelijk wordt uit de bovenstaande formule, is het berekenen van de buigtoeslag een eenvoudig proces.
Je kunt de buigtoeslag bepalen door de bovenstaande waarden in de formule te substitueren.
Wanneer de buighoek 90° is, kan de formule voor de buigtoeslag als volgt worden vereenvoudigd:
Opmerking: De K-factor voor de meeste standaardmaterialen en -diktes ligt meestal tussen 0 en 0,5.
Je kunt de waarde van de K-factor als volgt nauwkeurig berekenen K-factor rekenmachine:
De formule voor buigtoeslag (BA) is essentieel voor het berekenen van de materiaallengte die nodig is om een bocht te vormen. Deze algemene formule is breed toepasbaar op verschillende materialen en buigmethodes:
Waar:
De K-factor is cruciaal omdat deze de positie van de neutrale as aangeeft, die niet van lengte verandert tijdens het buigen. De K-factor ligt meestal tussen 0,3 en 0,5 en varieert op basis van het type materiaal, de dikte, de radius en de buigmethode.
Verschillende materialen hebben unieke eigenschappen die aanpassingen in de berekeningen van de buigtoeslag nodig maken. Deze aanpassingen zorgen voor nauwkeurigheid, vooral bij 90°-bochten:
Voor zachtere materialen zoals zacht messing of koper wordt de buigtoeslag als volgt berekend:
BA = (0,55 × T) + (1,57 × R
Deze aanpassing houdt rekening met de vervormbaarheid van het materiaal en de lagere weerstand tegen vervorming.
Voor halfhard koper of messing, zacht staal en aluminium is de buigtoeslag:
BA = (0,64 x T) + (1,57 x R)
Deze materialen hebben een gemiddelde hardheid en vereisen een iets hogere toeslag dan zachtere materialen.
Voor hardere materialen zoals brons, hard koper, koudgewalst staal en verenstaal is de formule:
BA = (0,71 x T) + (1,57 x R)
Deze materialen zijn beter bestand tegen buigen, waardoor een hogere toeslag nodig is.
Om de totale vlakke lengte van het plaatmetalen onderdeel te bepalen, wordt de buigtoeslag opgeteld bij de lengtes van de vlakke delen:
Platte lengte = beenlengte 1 + BA + beenlengte 2
Deze aanpak zorgt ervoor dat de uiteindelijke afmetingen van het onderdeel na het buigen nauwkeurig zijn.
Beschouw een 90° bocht in een plaat aluminium met een dikte van 2 mm en een inwendige buigradius van 5 mm. Gebruik de materiaalspecifieke formule voor halfhard koper, messing, zacht staal en aluminium:
BA = (0,64 × 2) + (1,57 × 5)
BA = 1,28 + 7,85=9,13
Als het onderdeel twee vlakke secties heeft van elk 50 mm, dan is de totale vlakke lengte:
Platte lengte = 50 + 9,13 + 50 = 109,13 mm
Naast de bochttoeslag zijn ook de bochtaftrek (BD) en de buitenste terugslag (OSSB) belangrijk voor nauwkeurige metingen:
Buigaftrek (BD) = OSSB - BA
Waar:
Deze formuleringen en overwegingen zijn essentieel voor het nauwkeurig berekenen van buigtoeslagen, zodat plaatwerkonderdelen met de juiste afmetingen en pasvorm worden gefabriceerd.
Buigtoeslag is een kritieke factor in het buigproces van plaatmetaal, vooral voor materialen als aluminium. Het houdt rekening met de materiaalrek die optreedt tijdens het buigen en zorgt voor nauwkeurige eindafmetingen. Hier bespreken we de specifieke formule die wordt gebruikt voor aluminium platen en de toepassing ervan.
De buigtoeslag voor een aluminium plaat kan worden berekend met de volgende formule:
𝐿=𝐿1+𝐿2-1.6𝑇
Waar:
De waarde 1,6𝑇 is empirisch afgeleid, wat betekent dat deze is vastgesteld door praktische experimenten en productie-ervaring. Deze factor houdt rekening met het gedrag van het materiaal tijdens het buigen en zorgt ervoor dat de uiteindelijke afmetingen nauwkeurig zijn.
Het is cruciaal om op te merken dat deze formule specifiek van toepassing is onder bepaalde voorwaarden:
Volg deze stappen om de uitzetmaat van de aluminium plaat te bepalen:
Deze berekening geeft je de vlakke patroonlengte die nodig is voor het buigen, zodat het uiteindelijke gebogen onderdeel de juiste afmetingen heeft.
De buigtoeslagcalculator hieronder vereenvoudigt het proces van het berekenen van de waarde van de buigtoeslag, die cruciaal is voor nauwkeurige plaatbewerking. De buigtoeslag is de lengte van de neutrale as tussen de buiglijnen, die helpt bij het bepalen van de juiste blenkmaat voor een gebogen onderdeel.
De buighoek, aangeduid als θ, is een cruciale parameter in de formule voor buigtoeslag. Het geeft de hoek weer waarin het plaatwerk wordt gebogen. De buighoek wordt meestal gemeten in graden, maar kan met de formule worden omgezet naar radialen:
De binnenstraal, weergegeven als r, is de straal van de binnenbocht van de bocht. Deze straal heeft een directe invloed op de hoeveelheid rek en compressie die tijdens het buigen in het materiaal optreedt. Een kleinere binnenradius resulteert in een grotere vervorming, waarmee rekening moet worden gehouden bij de berekening van de buigtoeslag.
De materiaaldikte, aangeduid als T, is de dikte van het plaatmetaal dat gebogen wordt. Dikkere materialen hebben meer last van uitrekking en samendrukking, wat de totale buigtoeslag beïnvloedt. Een nauwkeurige meting van de materiaaldikte is essentieel voor nauwkeurige berekeningen van de buigtoeslag.
De K-factor is een dimensieloze waarde die de positie van de neutrale as ten opzichte van de materiaaldikte weergeeft. De neutrale as is de theoretische lijn in het materiaal die onveranderd blijft in lengte tijdens het buigen. De K-factor varieert op basis van materiaaleigenschappen en buigmethodes en varieert meestal van 0,3 tot 0,5 voor de meeste materialen. De formule voor de positie van de neutrale as is:
Neutrale aspositie = K × T
De neutrale as is de denkbeeldige lijn in het materiaal waarvan de lengte tijdens het buigen onveranderd blijft. Inzicht in de positie ervan is cruciaal voor het berekenen van de juiste buigtoeslag.
De buigtoeslag, weergegeven als BA, is de lengte van de neutrale as die nodig is om een bocht te vormen. Het wordt berekend met de formule:
Deze formule gebruikt de buighoek, de binnenradius, de materiaaldikte en de K-factor om nauwkeurige berekeningen van de buigtoeslag te garanderen.
De buigtoeslagtabel is een essentieel hulpmiddel voor professionals die werken met plaatbewerking. Het biedt een uitgebreide lijst van belangrijke parameters zoals materiaaldikte, buigradius, buighoek, buigtoeslag en waarden voor buigaftrek voor veel voorkomende materialen. Deze informatie is cruciaal voor het nauwkeurig berekenen van de ontwikkellengte van een plaatwerkonderdeel na het buigen.
Verder lezen:
| TV | Hoek | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Kortste maat |
| V4 | 90 | 0.9 | 1.4 | 2.8 | ||||||||||
| V4 | 120 | 0.7 | ||||||||||||
| V4 | 150 | 0.2 | ||||||||||||
| V6 | 90 | 1.5 | 1.7 | 2.15 | 4.5 | |||||||||
| V6 | 120 | 0.7 | 0.86 | 1 | ||||||||||
| V6 | 150 | 0.2 | 0.3 | 0.4 | ||||||||||
| V7 | 90 | 1.6 | 1.8 | 2.1 | 2.4 | 5 | ||||||||
| V7 | 120 | 0.8 | 0.9 | 1 | ||||||||||
| V7 | 150 | 0.3 | 0.3 | 0.3 | ||||||||||
| V8 | 90 | 1.6 | 1.9 | 2.2 | 2.5 | 5.5 | ||||||||
| V8 | 30 | 0.3 | 0.34 | 0.4 | 0.5 | |||||||||
| V8 | 45 | 0.6 | 0.7 | 0.8 | 1 | |||||||||
| V8 | 60 | 1 | 1.1 | 1.3 | 1.5 | |||||||||
| V8 | 120 | 0.8 | 0.9 | 1.1 | 1.3 | |||||||||
| V8 | 150 | 0.3 | 0.3 | 0.2 | 0.5 | |||||||||
| V10 | 90 | 2.7 | 3.2 | 7 | ||||||||||
| V10 | 120 | 1.3 | 1.6 | |||||||||||
| V10 | 150 | 0.5 | 0.5 | |||||||||||
| V12 | 90 | 2.8 | 3.65 | 4.5 | 8.5 | |||||||||
| V12 | 30 | 0.5 | 0.6 | 0.7 | ||||||||||
| V12 | 45 | 1 | 1.3 | 1.5 | ||||||||||
| V12 | 60 | 1.7 | 2 | 2.4 | ||||||||||
| V12 | 120 | 1.4 | 1.7 | 2 | ||||||||||
| V12 | 150 | 0.5 | 0.6 | 0.7 | ||||||||||
| V14 | 90 | 4.3 | 10 | |||||||||||
| V14 | 120 | 2.1 | ||||||||||||
| V14 | 150 | 0.7 | ||||||||||||
| V16 | 90 | 4.5 | 5 | 11 | ||||||||||
| V16 | 120 | 2.2 | ||||||||||||
| V16 | 150 | 0.8 | ||||||||||||
| V18 | 90 | 4.6 | 13 | |||||||||||
| V18 | 120 | 2.3 | ||||||||||||
| V18 | 150 | 0.8 | ||||||||||||
| V20 | 90 | 4.8 | 5.1 | 6.6 | 14 | |||||||||
| V20 | 120 | 2.3 | 3.3 | |||||||||||
| V20 | 150 | 0.8 | 1.1 | |||||||||||
| V25 | 90 | 5.7 | 6.4 | 7 | 17.5 | |||||||||
| V25 | 120 | 2.8 | 3.1 | 3.4 | ||||||||||
| V25 | 150 | 1 | 1 | 1.2 | ||||||||||
| V32 | 90 | 7.5 | 8.2 | 22 | ||||||||||
| V32 | 120 | 4 | ||||||||||||
| V32 | 150 | 1.4 | ||||||||||||
| V40 | 90 | 8.7 | 9.4 | 28 | ||||||||||
| V40 | 120 | 4.3 | 4.6 | |||||||||||
| V40 | 150 | 1.5 | 1.6 |
| TV | Hoek | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Kortste maat |
| V4 | 1.4 | 2.8 | ||||||||||||
| V6 | 1.6 | 4.5 | ||||||||||||
| V7 | 1.6 | 1.8 | 5 | |||||||||||
| V8 | 1.8 | 2.4 | 3.1 | 5.5 | ||||||||||
| V10 | 2.4 | 3.2 | 7 | |||||||||||
| V12 | 2.4 | 3.2 | 8.5 | |||||||||||
| V14 | 3.2 | 10 | ||||||||||||
| V16 | 3.2 | 4 | 4.8 | 11 | ||||||||||
| V18 | 4.8 | 13 | ||||||||||||
| V20 | 4.8 | 14 | ||||||||||||
| V25 | 4.8 | 5.4 | 6 | 17.5 | ||||||||||
| V32 | 6.3 | 6.9 | 22 |
| Hoek | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Kortste maat |
| 90 | 3.6 | 5.2 | 6.8 | 8.4 | 28 | ||||||||
| 120 | |||||||||||||
| 150 |
| MATERIAAL | SPCC | SUS | Al (LY12) | SECC | ||||
|---|---|---|---|---|---|---|---|---|
| T | ΔT | ΔK | ΔT | ΔK | ΔT | ΔK | ΔT | ΔK |
| T=0.6 | 1.25 | 1.26 | ||||||
| T=0.8 | 0.18 | 1.42 | 0.15 | 1.45 | 0.09 | 1.51 | ||
| T=1.0 | 0.25 | 1.75 | 0.20 | 1.80 | 0.30 | 1.70 | 0.38 | 1.62 |
| T=1.2 | 0.45 | 1.95 | 0.25 | 2.15 | 0.50 | 1.90 | 0.43 | 1.97 |
| T=1.4 | 0.64 | 2.16 | ||||||
| T=1.5 | 0.64 | 2.36 | 0.50 | 2.50 | 0.70 | 2.30 | ||
| T=1.6 | 0.69 | 2.51 | ||||||
| T=1.8 | 0.65 | 3.00 | ||||||
| T=1.9 | 0.60 | 3.20 | ||||||
| T=2.0 | 0.65 | 3.35 | 0.50 | 3.50 | 0.97 | 3.03 | 0.81 | 3.19 |
| T=2.5 | 0.80 | 4.20 | 0.85 | 4.15 | 1.38 | 3.62 | ||
| T=3.0 | 1.00 | 5.00 | 5.20 | 1.40 | 4.60 | |||
| T=3.2 | 1.29 | 5.11 | ||||||
| T=4.0 | 1.20 | 6.80 | 1.00 | 7.00 | ||||
| T=5.0 | 2.20 | 7.80 | 2.20 | 7.80 | ||||
| T=6.0 | 2.20 | 9.80 | ||||||
Opmerking:
Een goed bijgehouden buigtoeslagtabel is een essentieel hulpmiddel in de plaatbewerkingsindustrie. Het zorgt voor precisie en efficiëntie in het buigproces, wat uiteindelijk leidt tot een hogere kwaliteit en nauwkeuriger afgewerkte producten. Door de waarden in de tabel te begrijpen en te gebruiken, kunnen ingenieurs en constructeurs optimale resultaten behalen bij hun projecten.
Bij plaatbewerking is precisie en nauwkeurigheid cruciaal om onderdelen van hoge kwaliteit te maken. Een van de sleutelfactoren die een belangrijke rol spelen in dit proces is de K-factor. Inzicht in de K-factor en de toepassing ervan bij de berekening van buigtoeslagen is essentieel voor constructeurs om onderdelen te maken die aan exacte specificaties voldoen en betrouwbaar presteren in diverse industrieën.
De K-factor is een dimensieloze waarde die de verhouding weergeeft tussen de afstand van de neutrale as en de materiaaldikte. De K-factor is cruciaal voor nauwkeurige berekeningen van de buigtoeslag, die de hoeveelheid materiaal bepaalt die nodig is om een gewenste buiging te verkrijgen. De neutrale as is een denkbeeldige lijn in het materiaal die tijdens het buigen niet van lengte verandert. Door de K-factor te begrijpen, kunnen fabrikanten voorspellen hoe het materiaal zich zal gedragen wanneer het wordt gebogen, waardoor nauwkeurige en efficiënte productieprocessen worden gegarandeerd.
De K-factor wordt berekend met de formule:
Waar:
Het gebruik van de K-factor in de formule voor buigtoeslag helpt bij het voorspellen van materiaalrek en -compressie tijdens het buigen. De formule voor buigtoeslag is:
Om dit te illustreren nemen we een eenvoudig voorbeeld door. Stel we hebben een plaatmetalen onderdeel met een dikte (T) van 2 mm, gebogen onder een hoek van 90 graden (θ), met een binnenradius (r) van 5 mm en een K-factor (K) van 0,4.
1. Converteer de buighoek naar radialen:
2. Pas de waarden toe op de formule voor de buigtoeslag:
Deze berekening laat zien dat er ongeveer 9,11 mm materiaal nodig is langs de neutrale as om de gewenste buiging te krijgen, wat het belang van een nauwkeurige K-factor aantoont.
De K-factor heeft een directe invloed op de nauwkeurigheid van de berekeningen van de buigtoeslag. Een nauwkeurige K-factor zorgt ervoor dat de uiteindelijke afmetingen van het gebogen onderdeel overeenkomen met de ontwerpspecificaties, waardoor minder materiaal wordt verspild en er minder nabewerking nodig is. Deze precisie is van vitaal belang voor industrieën waar exacte afmetingen cruciaal zijn voor de assemblage en functionaliteit van componenten.
Verschillende materialen hebben unieke mechanische eigenschappen, die resulteren in verschillende K-Factor waarden. Zachtere materialen zoals aluminium hebben meestal een lagere K-Factor, terwijl hardere materialen zoals roestvrij staal een hogere K-Factor hebben. Inzicht in deze variaties stelt fabrikanten in staat om de juiste K-Factor waarden te selecteren voor verschillende materialen, zodat nauwkeurige berekeningen en efficiënte productieprocessen gegarandeerd zijn.
Hieronder vindt u antwoorden op een aantal veelgestelde vragen:
De formule voor buigtoeslag wordt gebruikt om de lengte van de neutrale as van een buiging in plaatmetaal te berekenen, wat cruciaal is voor het bepalen van de juiste lengte van het vlakke patroon voordat het metaal wordt gebogen. Deze berekening zorgt ervoor dat de uiteindelijke afmetingen van het gebogen onderdeel overeenkomen met de ontwerpspecificaties.
De formule houdt rekening met verschillende belangrijke parameters:
De algemene formule voor buigtoeslag (BA) is:
Door deze formule te gebruiken, kunt u de exacte lengte van het materiaal berekenen dat nodig is om een bocht te vormen, waarbij u ervoor zorgt dat het materiaal niet te veel uitrekt of samendrukt. Deze berekende buigtoeslag wordt vervolgens opgeteld bij de beenlengtes van het onderdeel om een nauwkeurig vlak patroon te ontwikkelen, wat essentieel is voor het produceren van onderdelen met precieze afmetingen.
De formule voor buigtoeslag is ook gerelateerd aan buigaftrek, wat de lengte is die moet worden afgetrokken van de totale lengte van het plaatwerk om het juiste vlakke patroon te krijgen. De buigaftrek wordt berekend aan de hand van de buigtoeslag en de buitenste terugslag, zodat de uiteindelijke afmetingen van het onderdeel na het buigen nauwkeurig zijn.
Als je bijvoorbeeld een 2 mm dikke roestvast stalen plaat buigt in een hoek van 90° met een inwendige buigradius van 3 mm en een K-factor van 0,44, dan kan de buigtoeslag als volgt worden berekend:
Deze buigtoeslag wordt vervolgens gebruikt om ervoor te zorgen dat het vlakke patroon correct wordt ontwikkeld, wat resulteert in een onderdeel dat voldoet aan de ontwerpspecificaties. Samengevat is de formule voor de buigtoeslag essentieel voor nauwkeurige plaatbewerking, zodat de uiteindelijke onderdelen de juiste afmetingen hebben.
Om de buigtoeslag in plaatmateriaal te berekenen, moet je een aantal belangrijke parameters bepalen: materiaaldikte (T), buighoek (θ), binnenradius (r) en de K-factor (K). De buigtoeslag (BA) wordt berekend met de formule:
Hier is een stap-voor-stap proces:
Gebruik deze formule voor dezelfde parameters:
Door deze stappen te volgen en de juiste formule te gebruiken, kun je de buigtoeslag voor je plaatwerkonderdelen nauwkeurig berekenen, zodat je verzekerd bent van een nauwkeurige fabricage.
De K-factor is om verschillende redenen belangrijk in de formule voor buigtoeslag, die elk hun belang onderstrepen bij de vervaardiging van precisieplaatwerk. Ten eerste geeft deze de verhouding weer tussen de neutrale as en de materiaaldikte. Tijdens het buigen verschuift de neutrale as van zijn oorspronkelijke locatie op 50% van de materiaaldikte naar het binnenoppervlak van de bocht. Deze verschuiving is kritisch omdat het de hoeveelheid rek bepaalt die in het materiaal optreedt. De K-factor helpt bij het berekenen van deze nieuwe locatie, wat essentieel is voor nauwkeurige buigberekeningen.
Ten tweede is de K-factor van fundamenteel belang bij het berekenen van de buigtoeslag, wat de lengte is van de neutrale vezel van het begin tot het einde van de boog die door de buiging wordt gegenereerd. Deze berekening is nodig om de vlakke maat van het plaatmateriaal te bepalen die nodig is om de gewenste gebogen vorm te verkrijgen. De buigtoeslag wordt direct beïnvloed door de K-factor, omdat deze rekening houdt met de rek van het materiaal tijdens het buigproces.
Bovendien maakt het gebruik van de K-factor nauwkeurige berekeningen mogelijk van buigverminderingen, buitenste terugslagen en de algehele vlakke lay-out van het onderdeel. Deze precisie is van vitaal belang omdat het ervoor zorgt dat de uiteindelijke afmetingen van het gebogen onderdeel overeenkomen met de ontwerpspecificaties, waardoor fouten worden voorkomen die zouden kunnen ontstaan bij het gebruik van algemene of onnauwkeurige K-factorwaarden.
De K-factor varieert op basis van verschillende parameters, zoals het materiaaltype, de dikte, de vervormingsmethode, het gereedschap en de buighoek. Deze variabiliteit betekent dat de K-factor moet worden afgestemd op de specifieke omstandigheden van het buigproces. Door rekening te houden met deze factoren helpt de K-factor bij het aanpassen van de buigcompensatieformule om nauwkeurigere resultaten te verkrijgen.
Tot slot is een correcte waarde van de K-factor essentieel om fouten in de uiteindelijke afmetingen van de gevouwen plaat te voorkomen. Onjuiste K-factorwaarden kunnen leiden tot onnauwkeurigheden in de buigtoeslagen, wat resulteert in onderdelen die niet voldoen aan de vereiste specificaties. Daarom is het nauwkeurig bepalen en gebruiken van de K-factor essentieel voor het produceren van componenten van hoge kwaliteit.
Samengevat is de K-factor belangrijk omdat deze een nauwkeurige berekening van buigtoeslagen mogelijk maakt, rekening houdt met de verschuiving van de neutrale as en rekening houdt met de specifieke materiaal- en procesparameters, die allemaal essentieel zijn voor het bereiken van nauwkeurige en betrouwbare resultaten bij het buigen van plaatwerk.
De formule voor de buigtoeslag bij het buigen van plaat omvat gewoonlijk verschillende belangrijke variabelen:
De buigtoeslag (BA) kan worden berekend met de formule:
of
waarbij (0,017453) (π/180) is en (0,0078) (π /180) x K) - factor.
Deze variabelen zijn essentieel voor het nauwkeurig bepalen van de buigtoeslag, wat cruciaal is voor nauwkeurige plaatbewerking.
Ja, de formule voor buigtoeslag kan aanzienlijk variëren op basis van het materiaaltype en andere factoren zoals materiaaldikte, buighoek en het specifieke buigproces.
De K-factor, een kritische component van de formule voor buigtoeslag, vertegenwoordigt de verplaatsing van de theoretische neutrale as tijdens het buigen en varieert afhankelijk van het materiaal. Voor zacht koudgewalst staal wordt bijvoorbeeld meestal een K-factor rond 0,446 gebruikt, terwijl andere materialen zoals roestvrij staal en aluminium andere K-factoren hebben vanwege hun unieke eigenschappen en buiggedrag.
De formule voor de buigtoeslag houdt ook rekening met de materiaaldikte en de buighoek, die per materiaal kunnen verschillen. Een algemene vorm van de formule voor buigtoeslag is:
waar:
Verschillende materialen hebben verschillende eigenschappen zoals elasticiteit, treksterkte en korrelrichting die hun buiggedrag beïnvloeden. Aluminium buigt bijvoorbeeld gemakkelijker dan staal, waardoor aanpassingen in de berekening van de buigtoeslag nodig zijn. Bovendien kan het buigen van een metaal langs de vezelrichting meer kracht en een andere buigtoeslag vereisen dan het buigen dwars op de vezelrichting.
Er moet ook rekening worden gehouden met de neiging van het materiaal om terug te veren na het buigen, bekend als terugvering. Hierbij wordt het materiaal iets overgebogen om rekening te houden met elastisch herstel, dat wordt beïnvloed door het materiaaltype en de eigenschappen ervan.
Samengevat moet de formule voor buigtoeslag worden afgestemd op het specifieke materiaal dat wordt gebruikt, rekening houdend met de unieke eigenschappen, dikte en het buigproces.








