Hoe zorgen ingenieurs voor de sterkte en duurzaamheid van balken onder verschillende belastingen? Dit artikel gaat in op de principes van buigschuifspanning en de voorwaarden die nodig zijn om de sterkte van liggers te behouden. Het behandelt de spanningsverdeling in verschillende balkdoorsneden - rechthoekig, cirkelvormig, I-vormig en dunwandig ringvormig - en stelt manieren voor om de prestaties van balken te verbeteren door een beter ontwerp en materiaalgebruik. Leer hoe schuif- en buigspanningen op elkaar inwerken en ontdek praktische tips om de constructie en toepassing van liggers te optimaliseren.
Er is zowel een buigmoment als een afschuifkracht op de dwarsdoorsnede van een balk onderhevig aan dwarskracht, wat resulteert in zowel normaalspanning als afschuifspanning op de dwarsdoorsnede. De buigschuifspanning van een aantal veel voorkomende balkdoorsneden wordt hierna besproken.
Een klein segment met een lengte van dx wordt uit de balk gesneden onder dwarskracht buiging. De balk is onbelast en de dwarskrachten aan beide zijden van het segment zijn gelijk maar in tegengestelde richting. Het buigmoment op de rechter doorsnede is groter dan dat op de linker doorsnede, wat resulteert in verschillende normaalspanningen op de twee doorsneden.
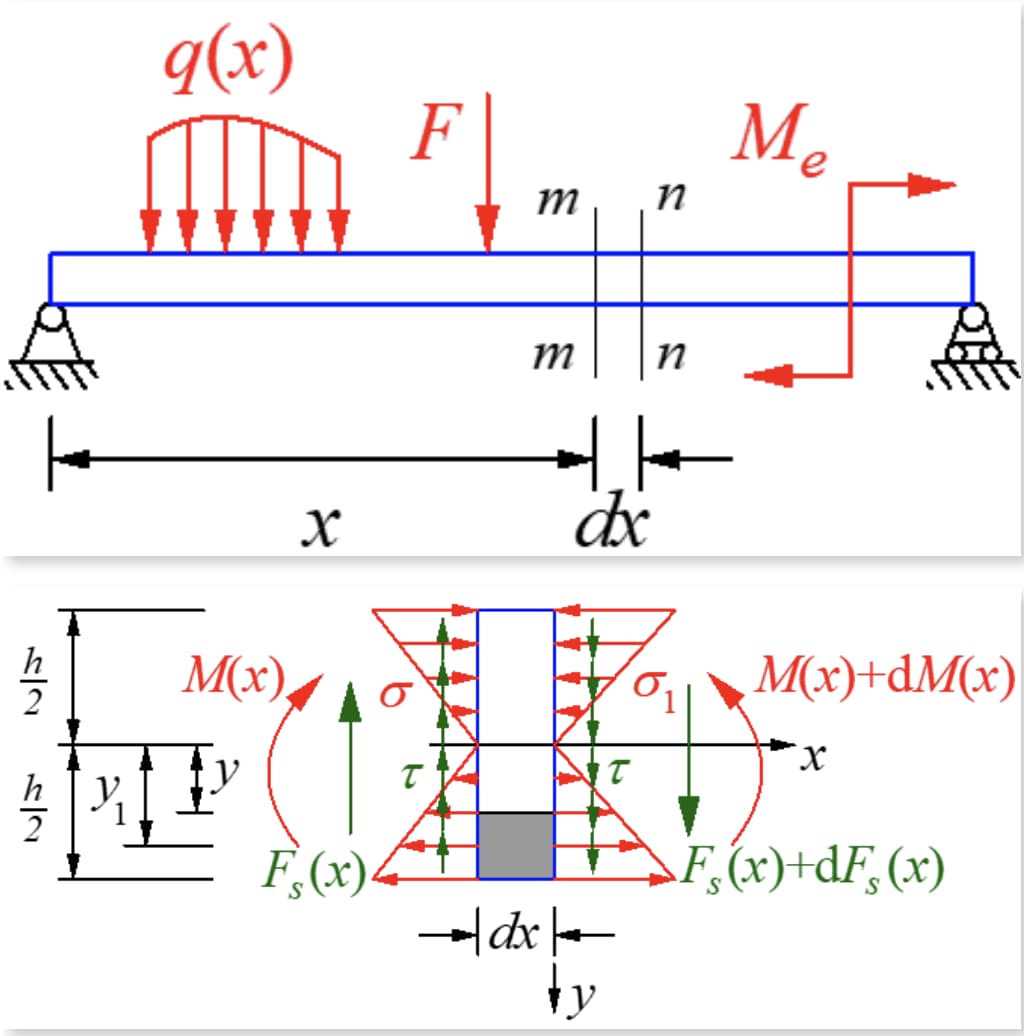
Voor een smalle rechthoekige doorsnede raakt de schuifspanning de grens aan beide zijden van de balk door de afwezigheid van schuifspanning aan de zijkant. Dit betekent dat, als de balk symmetrisch gebogen is en evenwijdig aan de begrenzing, de schuifspanning op de y-as van de symmetrieas moet liggen en weinig verandert langs de breedterichting.
Daarom worden de volgende aannames gedaan over de verdelingswet van schuifspanning op de dwarsdoorsnede:
Als de hoogte-breedteverhouding van de doorsnede groter is dan 2, is de oplossing op basis van bovenstaande aanname nauwkeurig genoeg vergeleken met de exacte oplossing uit de elastische theorie.
Volgens het wederkerigheidsbeginsel van schuifspanning moet er een schuifspanning zijn die gelijk is aan de grootte van de doorsnede op de lengtedoorsnede loodrecht op de doorsnede. Snijd een microsegment langs het langsvlak met de momentneutrale as weg van y, en neem het micro-element aan de onderkant van het langsvlak. De krachten zijn zoals aangegeven in de onderstaande figuur.
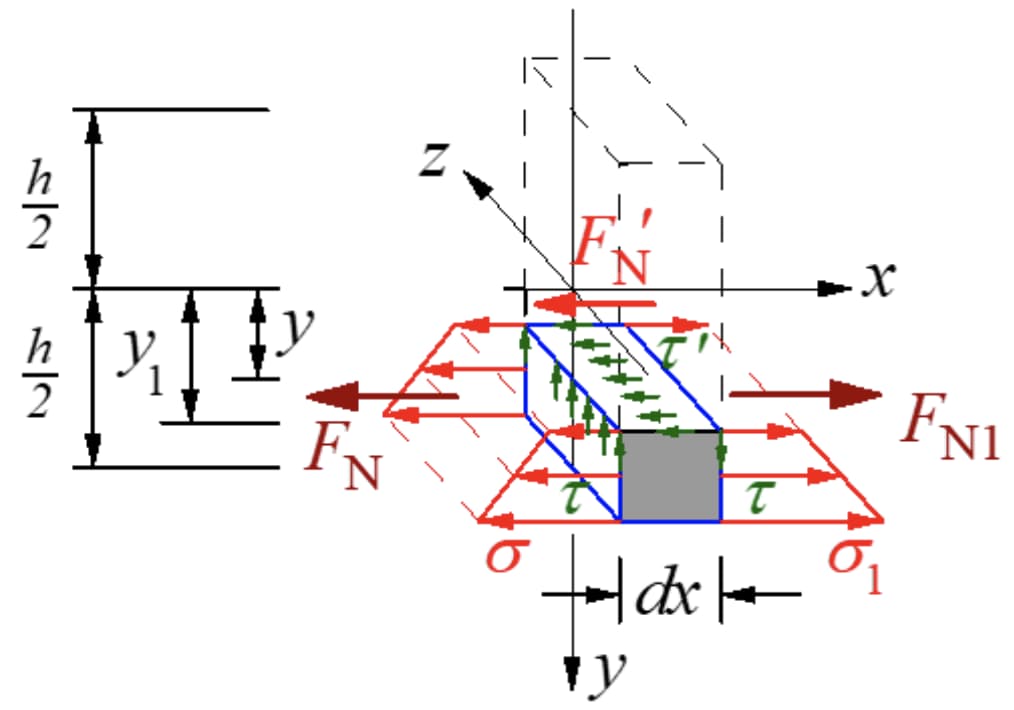
De resulterende kracht van de normaalspanning op de linker doorsnede is:
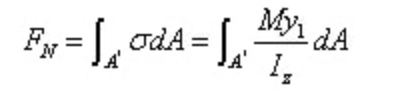
De resulterende kracht van de normaalspanning op de rechter doorsnede is：
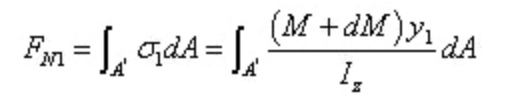
Het is duidelijk dat de twee resultanten van verschillende grootte zijn. Er moet een kracht in de axiale richting op de langsdoorsnede bestaan om het microsegment in evenwicht te houden. Deze kracht is het resultaat van schuifspanning, wat de aanwezigheid van schuifspanning op de lengtedoorsnede bevestigt.
Aangezien dx een kleine hoeveelheid is, moet de schuifspanning op het langsvlak gelijkmatig worden verdeeld：
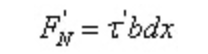
Volgens de evenwichtsvoorwaarden：
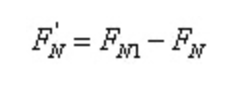
Dat wil zeggen,
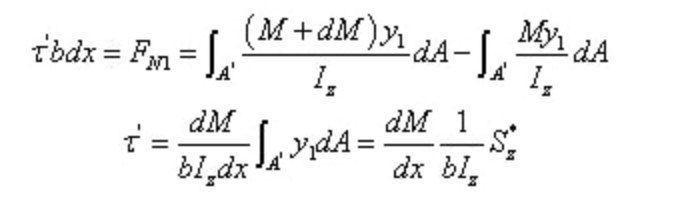
Onder,
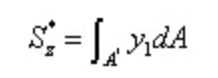
Uit de reciproke stelling van schuifspanning en de differentiële relatie tussen schuifkracht en buigmoment:
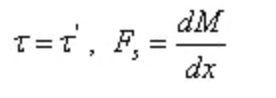
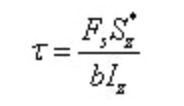
Waarvan:
Onder,
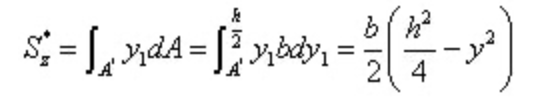
Substitueer in de formule voor de berekening van de schuifspanning
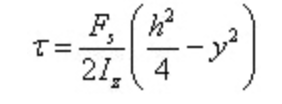
De schuifspanning is paraboolvormig verdeeld over de doorsnedehoogte.
Wanneer y=0, is er de maximale schuifspanning op de doorsnede bij de neutrale as
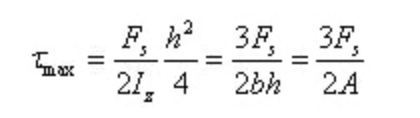
Hoekvervorming is
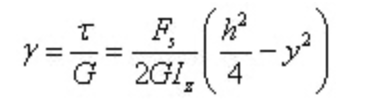
Het is te zien dat de hoekrek ook paraboolvormig verdeeld is over de doorsnedehoogte.
Op dit moment is de krommingsvorm van de dwarsdoorsnede wanneer de dwarskracht buigt te zien in de onderstaande figuur, die verifieert dat de dwarskracht buigvervorming niet voldoet aan de vlakke aanname.
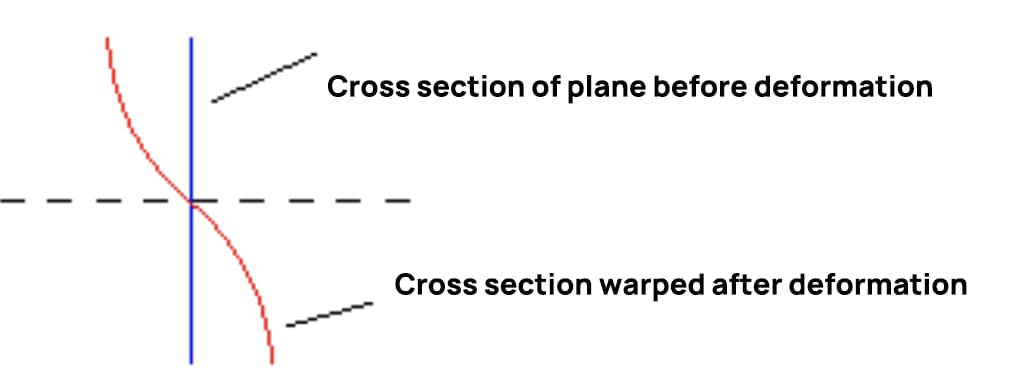
Als de schuifkracht constant blijft, is de schuifspanning op opeenvolgende doorsneden gelijk en is de mate van kromtrekken ook gelijk. De lengte van de longitudinale vezels verandert niet door het kromtrekken van de doorsnede, dus dit zal niet resulteren in extra normaalspanning. Als de schuifkracht verandert met de positie van de doorsnede, zal de mate van kromtrekken op opeenvolgende twee doorsneden verschillend zijn, wat leidt tot extra normaalspanning op de doorsnede.
Voor symmetrische doorsneden met andere vormen kan de benaderende schuifspanningsoplossing worden afgeleid met de bovenstaande methode.
Voor een rechthoekige doorsnede is in de spanningsberekeningsformule de doorsnedebreedte (b) constant en is het statische moment van de helft van de doorsnede aan één kant van de neutrale as ten opzichte van de neutrale as het grootst. Als gevolg daarvan is de schuifspanning op elk punt van de neutrale as het grootst.
Voor symmetrische doorsneden van andere vormen is de maximale schuifspanning op de doorsnede meestal gelokaliseerd op verschillende punten op de neutrale as, met uitzondering van doorsneden met een aanzienlijk grotere breedte op de neutrale as (zoals dwarsdoorsneden) of sommige doorsneden met variabele breedte (zoals gelijkbenige driehoekdoorsneden).
Daarom zal voor I-vormige, ringvormige en cirkelvormige liggers de maximale schuifspanning op elk punt van de neutrale as hieronder hoofdzakelijk worden besproken.
De schuifspanning op elk punt van de rand van een cirkelvormige doorsnede raakt de omtrek, volgens de reciproke stelling van schuifspanning. In elk punt van de symmetrieas moet de schuifspanning in de y-richting zijn. De verdeling van schuifspanning kan worden verondersteld te convergeren in een punt op de symmetrieas voor elk punt langs de breedte y vanaf de neutrale as, en de componenten van schuifspanning langs de Y-richting op elk punt langs de breedte zijn gelijk.
De maximale schuifspanning van de cirkelvormige doorsnede ligt nog steeds op de neutrale as en de richting is evenwijdig aan de externe kracht, met dezelfde waarde op elk punt op de neutrale as.
De maximale schuifspanning is
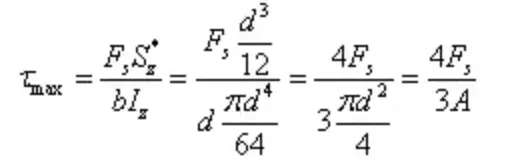
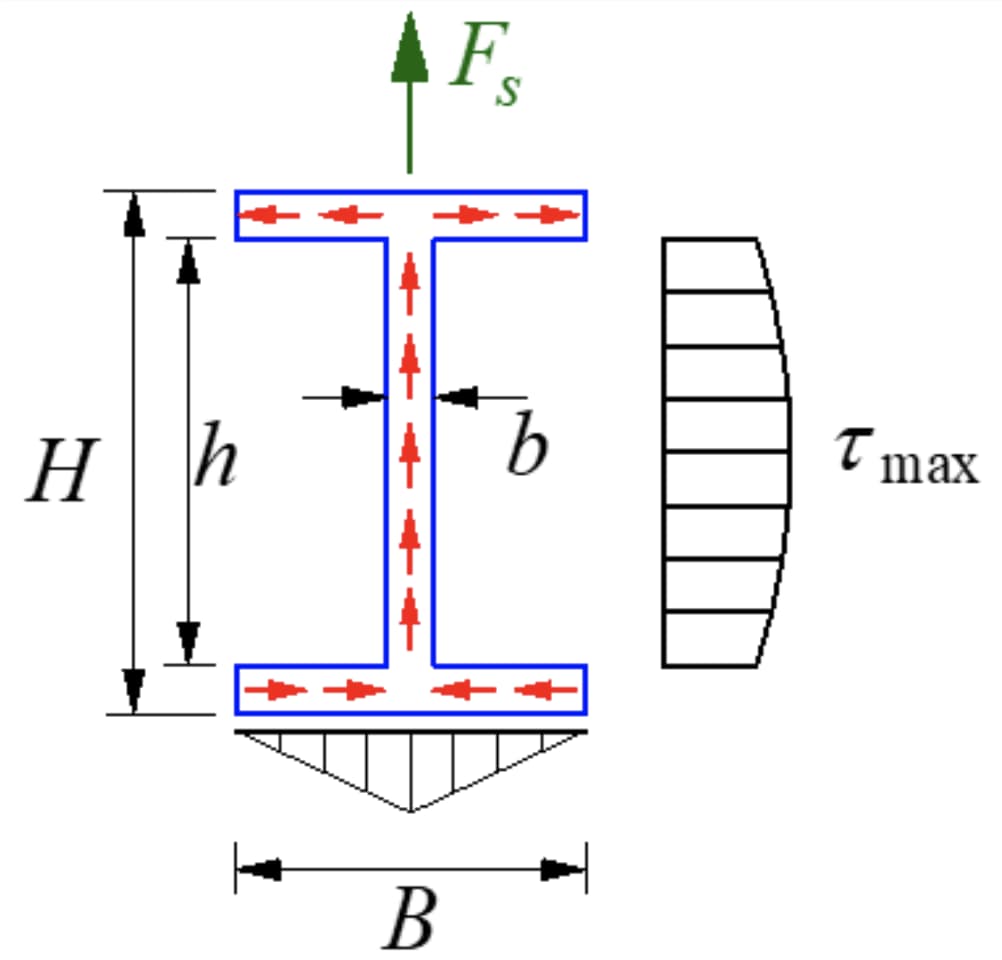
De I-vormige doorsnede is een dunwandige open doorsnede met een spanningsverdeling zoals weergegeven in de figuur. De grootte van de schuifspanning langs de wanddikte is gelijk, bekend als schuifspanningstroming, die in de schuifrichting vloeit.
De component van schuifspanning parallel aan de y-as op de flens is secundair en verwaarloosbaar, met de nadruk op de component parallel aan de lange zijde van de flens. De schuifspanning op het lijf heeft een parabolische verdeling, waarvan de grootte wordt weergegeven in de figuur.
De maximale schuifspanning bevindt zich op de neutrale as.
In geval van I-vormig staalde maximale schuifspanning:
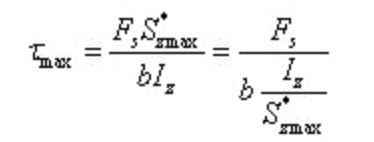
Waarbij b de dikte van de baan is en Iz/s*zmax kan worden verkregen door de profielstaaltabel te raadplegen.
Als het een I-vormige doorsnede is die bestaat uit drie lange en smalle rechthoeken, dan kunnen de maximale en minimale schuifspanningen op het lijf als volgt worden verkregen:
Uit de bovenstaande twee formules blijkt dat de breedte van het lijf veel kleiner is dan de breedte van de flens, zodat de maximale schuifspanning op het lijf niet veel verschilt van de minimale schuifspanning.
Daarom kan worden aangenomen dat de schuifspanning op het lijf ongeveer gelijk verdeeld is.
De resulterende schuifspanning op het lijf is goed voor 95-97% van de totale schuifkracht en de schuifkracht op de doorsnede wordt grotendeels gedragen door het lijf.
Aangezien het lijf bijna alle dwarskracht op de doorsnede draagt en de dwarskracht op het lijf bijna gelijkmatig verdeeld is, kan de maximale dwarskracht bij benadering berekend worden door de dwarskracht te delen door de dwarsdoorsnede van de ventrale pool:
Tegelijkertijd is het hele gebied van I-balk De flens is het verst verwijderd van de neutrale as en de normaalspanning op elk punt is relatief groot, zodat de flens het grootste deel van het buigmoment op de doorsnede draagt.
De dikte van dunwandige ringvormige doorsnede is d, de gemiddelde straal van de ring is r, en de dikte is veel kleiner dan de gemiddelde straal, dus kan worden aangenomen dat:
De schuifspanning op de dwarsdoorsnede is gelijk langs de wanddikte;
De schuifspanningsrichting raakt de middellijn van de doorsnede en de schuifspanningsrichting loopt langs de schuifrichting.
De maximale schuifspanning bevindt zich op de neutrale as:
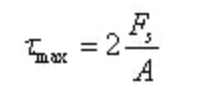
Waarbij A de oppervlakte van de ringvormige doorsnede is.
Buignormale spanningsconditie:
Voor neutrale asymmetrische doorsneden zijn de maximale treknormaalspanning en de maximale druknormaalspanning gelijk.
Plastic materialen worden vaak gebruikt en hun sterktevoorwaarden:
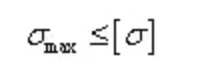
Voor de doorsnede met asymmetrische neutrale as zijn de maximale treknormaalspanning en de maximale druknormaalspanning niet gelijk.
Er worden vaak brosse materialen gebruikt en hun sterktevoorwaarden:
De sterkteconditie van buigschuifspanning is:
De buignormale spanning is de belangrijkste factor die de balk controleert.
Daarom is de sterkteconditie van buignormale spanning vaak de belangrijkste basis voor het ontwerp van liggers.
Om de draagkracht van de ligger te verbeteren, moeten vanuit de sterktetoestand twee aspecten in overweging worden genomen:
Aan de ene kant moet de spanning van de balk redelijk geregeld zijn om het maximale buigmoment te verminderen;
Aan de andere kant wordt een redelijke doorsnedevorm aangenomen om de buigcoëfficiënt van de doorsnede te verbeteren en de eigenschappen van het materiaal volledig te benutten.
Verbeter de spanningstoestand van de balk en probeer het maximale buigmoment in de balk te verminderen.
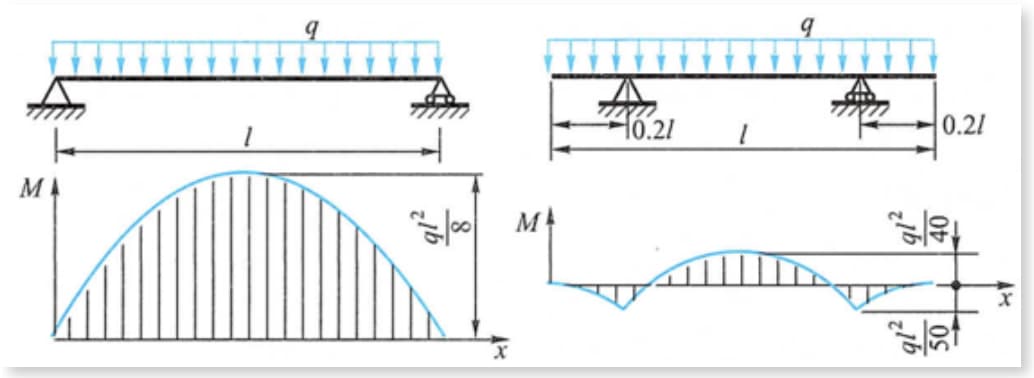
Zoals in de afbeelding te zien is, wordt het maximale buigmoment op de balk onder uniforme belasting sterk verminderd als de steun over een bepaalde afstand van de posities van beide uiteinden van de balk naar binnen wordt verplaatst.
Bijvoorbeeld, de ligger en cilindrische container van de portaalkraan, waarvan het steunpunt iets naar het midden beweegt, kunnen het effect bereiken van het verminderen van het maximale buigmoment.
Hoe groter de doorbuigingcoëfficiënt, hoe kleiner de spanning en hoe hoger de draagkracht van de balk.
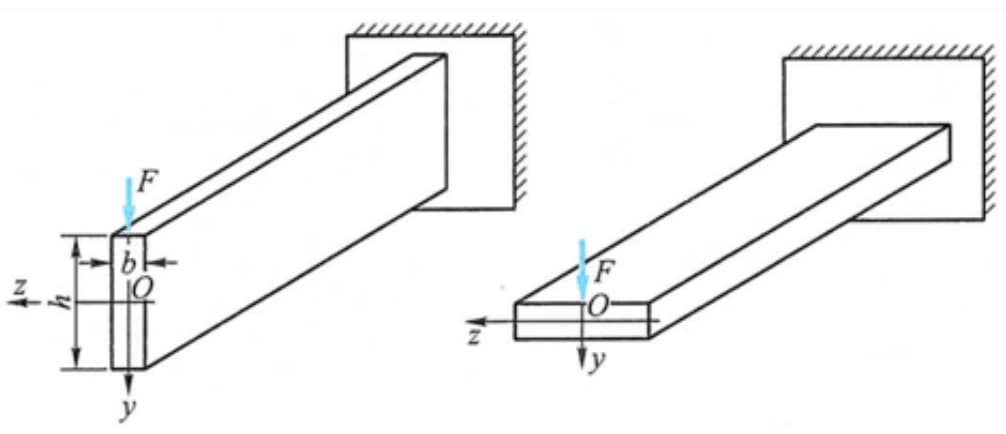
Wanneer de balk bijvoorbeeld in verticale richting wordt belast, is de buigsectiecoëfficiënt groter wanneer de doorsnede verticaal wordt geplaatst, dus is het verstandiger om deze verticaal te plaatsen dan horizontaal.
Terwijl we de buigsectiecoëfficiënt van de doorsnede verbeteren, hopen we ook minder materialen te gebruiken om zuiniger te werken.
Daarom wordt de verhouding tussen de buigsectiecoëfficiënt en het profieloppervlak over het algemeen gebruikt om de rationaliteit van het profielontwerp te meten.
Bij dezelfde dwarsdoorsnede is een rechthoekige doorsnede (hoogte groter dan breedte) redelijker dan een cirkelvormige doorsnede, terwijl een I-vormige doorsnede of een doosvormige doorsnede redelijker is dan een rechthoekige doorsnede.
Om materialen ten volle te benutten, moeten ze daarom zo ver mogelijk van de neutrale as worden geplaatst.
Bij het bespreken van de redelijke vorm van de doorsnede is de mechanische eigenschappen van het materiaal moet ook in aanmerking worden genomen.
Materialen met dezelfde trek- en druksterkte (zoals laag koolstofstaal) moeten neutrale asymmetrische profielen gebruiken, zoals cirkelvormig, rechthoekig, I-vormig, doos, enz.
Op deze manier kunnen de maximale trekspanning en de maximale drukspanning aan de boven- en onderrand van de doorsnede gelijk zijn.
Voor materialen met ongelijke trek- en druksterkte (zoals gietijzer, cement, enz.) moet de doorsnedevorm worden gebruikt met de neutrale as hellend naar de trekzijde.
De hierboven besproken balken hebben allemaal een gelijke doorsnede en de buigsectiecoëfficiënt is constant, maar in het algemeen verandert het buigmoment van elke doorsnede van de balk met de positie van de doorsnede.
Het doorsnedeontwerp van een gelijke rechte balk moet worden uitgevoerd op basis van het maximale buigmoment en de maximale spanning ligt dicht bij de toelaatbare spanning.
Het buigmoment op andere secties is klein, dus de spanning is klein en het materiaal wordt niet volledig benut.
Om materialen te besparen en het eigen gewicht te verminderen, kan de sectiegrootte worden gewijzigd zodat de buigsectiecoëfficiënt verandert met het buigmoment.
Een grotere doorsnede wordt gebruikt waar het buigmoment groter is, terwijl een kleinere doorsnede wordt gebruikt waar het buigmoment kleiner is.
Dit soort balk waarvan de doorsnede langs de as verandert, wordt balk met variabele doorsnede genoemd.
Als de maximale normaalspanning op elke doorsnede van een ligger met variabele doorsnede gelijk is aan de toelaatbare spanning, wordt het een ligger met gelijke sterkte genoemd.
Als oprichter van MachineMFG heb ik meer dan tien jaar van mijn carrière gewijd aan de metaalbewerkingsindustrie. Door mijn uitgebreide ervaring ben ik een expert geworden op het gebied van plaatbewerking, verspaning, werktuigbouwkunde en gereedschapsmachines voor metalen. Ik denk, lees en schrijf voortdurend over deze onderwerpen en streef er voortdurend naar om voorop te blijven lopen in mijn vakgebied. Laat mijn kennis en expertise een aanwinst zijn voor uw bedrijf.
NL 
EN 
AR 
DE 
ES 
FR 
IT 
JA 
PT 
PT_BR 
RU 
KO