Berekening van de buigsterkte van profielstaal: Een uitgebreide gids

Eerste deel: Inleiding

1. Concept:

Ondersteunt zijdelingse belastingen zoals vloerbalken, kraanbalken, gordingen, bruggen enz.

2. Classificatie:

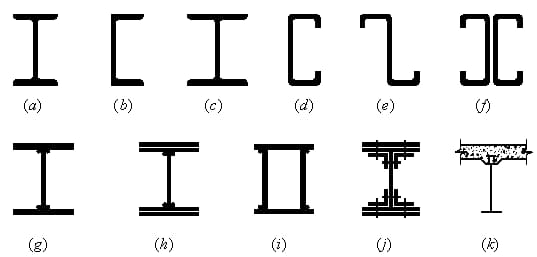
(1) Massieve web：

H-vormige staalsectie: Gemakkelijk te verwerken, eenvoudig te produceren en lage kosten.

Samengestelde sectie: Wanneer het H-vormige staal niet kan voldoen aan de eisen van sterkte en stijfheid.

(2) Roosterstructuur:

Als de overspanning groter is dan 40 m, kun je het beste een tralieligger gebruiken.

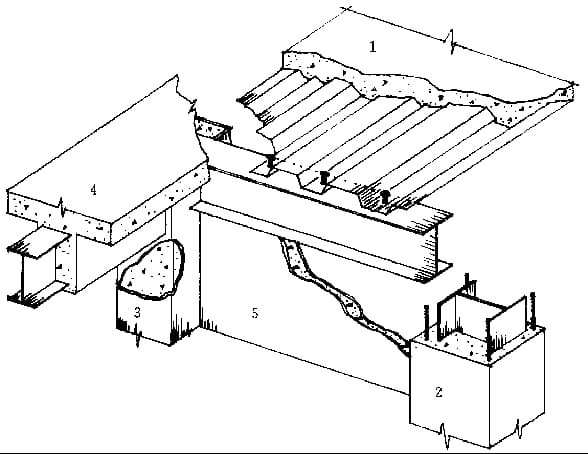
3. Straalrooster:

Een vlak systeem dat bestaat uit hoofd- en secundaire liggers die elkaar verticaal en horizontaal kruisen.

(1) Vereenvoudigd bundelrooster: Enkele hoofdstraal.

(2) Gewoon balkenrooster: Verdeeld in hoofd- en secundaire liggers.

(3) Samengesteld liggerrooster: Verdeeld in hoofdliggers, horizontale en verticale secundaire liggers.

4. Interactie tussen balken en platen:

(1) Samenwerking: Samengestelde vloerplaat.

(2) Niet-meewerkend werk: Algemene gewapende betonplaat.

Sectie twee: Buigsterkte.

De ontwikkeling van de normaalspanning in de doorsnede kan in drie fasen worden verdeeld:

(1) Elastische fase: Onder dynamische belasting.

(2) Elastisch-plastische fase: Onder statische belasting of indirecte dynamische belasting.

(3) Plastic podium:

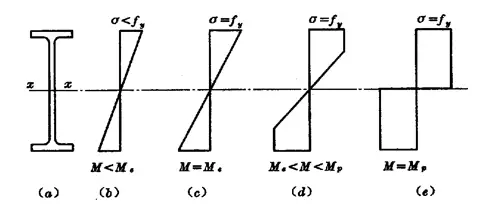
Buigcapaciteit tijdens de elastisch-plastische fase van een doorsnede:

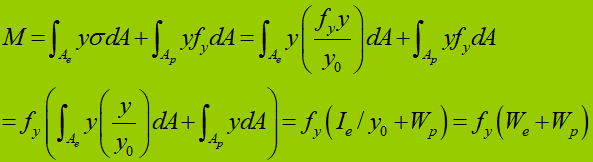
Voor een rechthoekige doorsnede:

(1) Elastische fase:

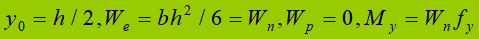
(2) Plastic podium:

(3) Elastisch-plastische fase:

Sectie vormfactor:

Sectie drie: Formules voor het berekenen van de sterkte aangenomen door codes.

I. Buignormale spanning:

Gedeeltelijke doorsnede plastische ontwikkeling (1/4 doorsnede, a = h/8) als grenstoestand:

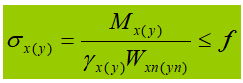
In de formule:

γ is de partiële veiligheidsfactor voor het moment, die kan worden bepaald op basis van tabel 5.1 in hoofdstuk 5 van de ontwerpcode.

Er zijn twee gevallen waarin de gedeeltelijke veiligheidsfactor voor het moment 1,0 moet zijn.

II. Schuifsterkte:

Methode:

S:

De schuifsterkte kan worden berekend met behulp van de schuifstroomtheorie, ervan uitgaande dat deze gelijkmatig is verdeeld langs de dikterichting van de dunne wand.

(1) Bij het berekenen van de verticale schuifspanning op een willekeurig punt van het lijf is het noodzakelijk om het traagheidsmoment van het brutodeel boven of onder dat punt ten opzichte van de neutrale as x te berekenen.

(2) Bij het berekenen van de horizontale schuifspanning in een willekeurig punt op de flens, is het noodzakelijk om het traagheidsmoment van de doorsnede links of rechts van dat punt ten opzichte van de neutrale as x te berekenen.

Waar t_w is de dikte van de doorsnede op de plaats waar de schuifspanning wordt berekend.

III. Lokale knikspanning van het lijf:

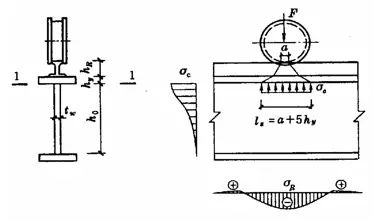
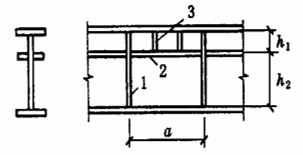
Wanneer de flens van een ligger wordt blootgesteld aan een grote vaste centrale belasting (inclusief oplegreacties) en er geen verstijvers zijn aangebracht volgens afbeelding 5-5 (a), of wanneer deze wordt blootgesteld aan een mobiele geconcentreerde belasting (zoals de wieldruk van een kraan) volgens afbeelding 5-5 (b), moet de lokale druksterkte aan de rand van de lijfhoogte worden berekend. Ervan uitgaande dat de geconcentreerde belasting zich vanaf het aangrijpingspunt verspreidt over een hoogtebereik van h_y in een verhouding van 1:2,5 en verspreidt zich in een verhouding van 1:1 binnen een hoogtebereik van h_Rwordt het gelijkmatig verdeeld over de hoogte van de baan randberekening. De resulterende σ_c ligt zeer dicht bij de maximale theoretische lokale druk. De lokale druksterkte kan worden berekend met de volgende formule:

In de formule,

• F - geconcentreerde belasting, die moet worden vermenigvuldigd met de dynamische coëfficiënt voor dynamische belastingen;
• ψ - de versterkingsfactor van de geconcentreerde belasting. Voor de wieldruk van een zware kraan op werkniveau is ψ = 1,35; voor andere belastingen is ψ = 1,0;
• l_z - de veronderstelde verdeellengte van een puntbelasting op de berekende hoogte van de lijfplaat. Voor een geconcentreerde belasting in het midden van de overspanning is l_z=a+5h_y+2h_Rvoor de reactiekracht aan het uiteinde van de balk, l_z=a+2,5h_y+a₁;
• a - de draaglengte van een geconcentreerde last in de overspanningsrichting. Als er geen gegevens beschikbaar zijn voor de druk van het kraanwiel, kan deze worden genomen als 50 mm;
• h_y - de afstand van de bovenkant van de balk tot de berekende hoogte van de lijfplaat;
• h_R - de hoogte van het spoor. Als er geen spoor is aan de bovenkant van de balk, is h_R=0;
• a₁ - de afstand van het uiteinde van de balk tot de buitenrand van de steunplaat en deze waarde mag niet groter zijn dan 2,5h_y.

Als de berekening niet bevredigend is, kan de dragende vaste geconcentreerde belasting of ondersteuning worden verstevigd door het plaatsen van dwarsverstijvers of het aanpassen van de doorsnede. Bij bewegende puntlasten kan echter alleen de doorsnede aangepast worden.

IV. Equivalente spanning onder complexe spanningstoestand.

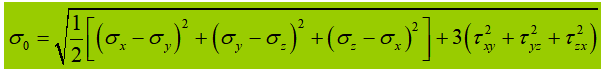
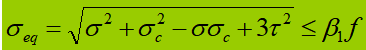
Wanneer de buiktriller wordt onderworpen aan een aanzienlijke normaalspanning, schuifspanning of plaatselijke drukspanning op de berekende hoogte, moet de equivalente spanning op die locatie worden berekend.

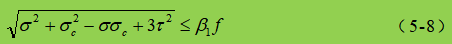
In de formule:

σ, τ, σ_c - buignormale spanning, schuifspanning en plaatselijke drukspanning op hetzelfde punt van de berekeningshoogte van de buikplaat, positief voor trekspanning en negatief voor drukspanning;

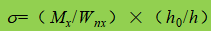
β₁ - coëfficiënt voor het verhogen van de ontwerpwaarde van de druksterkte op een lokaal punt. Als σ en σc hetzelfde teken hebben of σ_c=0, β₁=1,1; als σ en σc tegengestelde tekens hebben, is β₁=1.2.

Hoofdstuk Vier: Algehele stabiliteitsberekening van balken

1. Basisconcepten

Algemeen verschijnsel van instabiliteit:

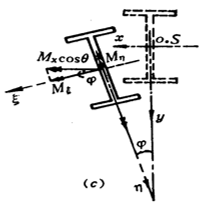
Analyse van het mechanisme: 

Nadat de balk door buiging is vervormd, wordt de bovenflens aan samendrukking onderworpen. Door onvoldoende laterale stijfheid van de balk zal de balk een laterale knikvervorming ondergaan. De buigvervorming in het vlak veroorzaakt door het moment treedt ook op samen met torsievervorming als gevolg van ongelijke buiging van boven naar beneden in de ligger.

Daarom neemt de algehele instabiliteit van de balk de vorm aan van buiging-torsiebuiging, of nauwkeuriger, buiging in de dwarsrichting en torsiebuiging.

2. Berekeningsformule voor het kritieke buigmoment van een eenvoudig ondersteunde balk met symmetrische doorsnede:

(1) C1, C2, C3 - Gerelateerd aan type belasting

(2) Iy, Iw, It - traagheidsmoment van de doorsnede

(3) L - Niet-verstevigde lengte in dwarsrichting

(4) a - Plaats van het actiepunt in de hoogterichting.

(5)

De belangrijkste factoren die de algehele stabiliteit van stalen balken beïnvloeden zijn:

(1) De ongeremde lengte in de dwarsrichting of de afstand L1 tussen het laterale steunpunt van de samengedrukte flens. Hoe kleiner de waarde van L1, hoe beter de algemene stabiliteit van de ligger en hoe hoger het kritieke buigmoment.

(2) De grootte van de dwarsdoorsnede, inclusief verschillende traagheidsmomenten. Hoe groter het traagheidsmoment, hoe beter de totale stabiliteit van de ligger. In het bijzonder kan het vergroten van de breedte van de samengedrukte flens b1 ook de waarde van βy in de formule verhogen.

(3) De beperkingen op de doorsnede door de eindsteunen van de ligger. Als de beperkingen op de rotatie rond de y-as van de doorsnede verbeterd kunnen worden, zal de algehele stabiliteit van de ligger sterk verbeteren.

(4) Soort belasting: Zuivere buiging, gelijkmatig verdeelde belasting, geconcentreerde belasting in het midden van de overspanning.

(5) De locatie van het aangrijpingspunt van de belasting langs de hoogterichting van de doorsnede, een waarde; negatief voor de bovenste flens en positief voor de onderste flens.

3. Controle van de algemene stabiliteit

Buigen in één vlak:

4. Algemene stabiliteitscoëfficiënt

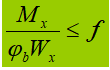
1. Gelaste I-vormige dwarsdoorsnede, tweeassig symmetrisch, zuiver buigbelasting.

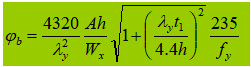
2. Gelaste I-vormige doorsnede, uniaxiaal symmetrisch (effecten van asymmetrische doorsnede en verschillende belastingen)

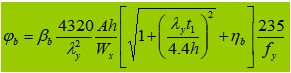
Als φ_b>0,6, wordt de stabiliteitscoëfficiënt genomen als:

3. Gewalste gewone I-vormige stalen eenvoudig ondersteunde balk.

4. Warmgewalste stalen kanaalplaat met eenvoudig ondersteunde balk.

5. Een dubbelassige symmetrische I-vormige cantileverbalk.

5. Zorg voor algehele stabiliteit.

De samengedrukte flens van de balk is bedekt met een deklaag (gewapend beton of staalplaat) en stevig verbonden om zijdelingse verplaatsing van de samengedrukte flens te voorkomen.

Voor eenvoudig ondersteunde H-balken of I-balken mag de verhouding van de vrije lengte L1 tot de breedte b van de samengedrukte flens niet groter zijn dan de in tabel 5.4 aangegeven waarde.

Tabel 5.4: Maximale waarde van L1/b1 waarvoor geen globale stabiliteitsberekening nodig is voor eenvoudig ondersteunde H- of I-balken.

6. Verificatiestappen voor algehele stabiliteit:

1. Bepaal of algehele stabiliteitskeuring vereist is.

2. Bereken de sectieparameters.

3.Verkrijg de equivalente kritische buigmomentcoëfficiënt βb volgens de belastingsomstandigheden.

4. Vervang de waarden door de formules om de totale stabiliteitscoëfficiënt ϕb te verkrijgen en controleer de totale stabiliteit.

Voorbeeld: 5-2，5-3

Hoofdstuk 5 - Lokale stabiliteit en verstijvingsontwerp van liggers

1. Overzicht:

Flensplaat: De belasting is relatief eenvoudig en de lokale stabiliteit wordt verzekerd door de breedte-dikteverhouding van de plaat te beperken.

Webplaat: De belasting is complex en om aan de sterktevereisten te voldoen, is de doorsnedehoogte vaak groot. Als we de hoogte-dikte verhouding van de staalplaat blijven beperken, zal de waarde van de staalplaat erg groot worden, wat oneconomisch is. Daarom worden verstijvers over het algemeen gebruikt om de grootte van de plaat te verkleinen en het draagvermogen van de lokale stabiliteit te verbeteren.

1. Dwarsverstijvers

2. Langsverstijvers

3. Korte verstijvers

2. Lokale stabiliteit van de vleugelflensplaat.

Ontwerpprincipe: principe van gelijke sterkte.

Volgens het elastische ontwerp (met γ=1,0 voor het buiten beschouwing laten van de plastische ontwikkeling) is de invloed van restspanningis de werkelijke doorsnede de elastisch-plastische fase ingegaan. De "specificatie" neemt E_t=0.7E.

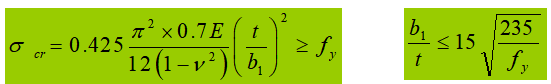
Als plastische ontwikkeling in aanmerking wordt genomen (γ > 1,0), zal de plastische ontwikkeling groter zijn en E_t=0.5E.

3. Buiging van webplaat

Nee.	De toestand van de webplaat.		Specificaties stijfselopstelling
1		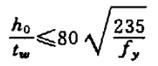στ=0	Verstijvers kunnen worden weggelaten.
2		στ≠0	Het wordt aanbevolen om dwarsverstijvers te installeren die voldoen aan de constructie- en berekeningsvereisten.
3			Het wordt aanbevolen om dwarsverstijvers te installeren die voldoen aan de constructie- en berekeningsvereisten.
4	De samengedrukte flens is beveiligd tegen verdraaien.		Langsverstijvers moeten worden toegevoegd in de compressiezone van de doorsnede waar de buigspanning hoog is, zodat wordt voldaan aan de constructie- en berekeningsvereisten.
5	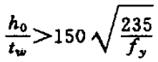De samengedrukte flens kan vrij draaien.
6	Indien nodig voor berekeningen.
7	Wanneer de plaatselijke drukspanning hoog is.		Indien nodig moeten korte verstijvers worden aangebracht in de drukzone om te voldoen aan de constructie- en berekeningsvereisten.
8	Bij de balksteun		Het is raadzaam om steunverstevigingen te installeren die voldoen aan de constructie- en berekeningsvereisten.
9	Wanneer de flens wordt blootgesteld aan een grote vaste geconcentreerde belasting.
10	In ieder geval		h0/tw mag niet hoger zijn dan

1. Knikken van samengestelde belaste platen

Alleen de staalplaat met dwarsverstijvers is geconfigureerd.

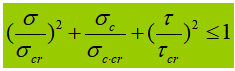
De webplaat is tegelijkertijd geconfigureerd met verstijvers in dwars- en langsrichting.

(1) Tussen samengedrukte flens en langsverstijvers.

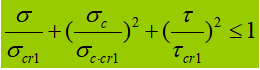
(2) Tussen trekflens en langsverstijvers.

Korte dwarsverstijvers worden geïnstalleerd tussen de samengedrukte flens en langsverstijvers.

2. Constructievereisten van verstijvers voor webplaat

(1) Stalen dwarsverstijvers geconfigureerd in paren aan beide zijden van de lijfplaat.

Naar buiten uitstekende breedte:

Dikte:

(2) Stalen dwarsverstijvers geconfigureerd aan één zijde van de lijfplaat.

Naar buiten uitstekende breedte: moet groter zijn dan 1,2 keer de waarde berekend volgens de bovenstaande formule.

Dikte: mag niet minder zijn dan 1/15 van de naar buiten uitstekende breedte.

(3) In de staalplaat die versterkt is met zowel dwars- als langsverstijvers, moeten de langsverstijvers worden losgemaakt op hun snijpunten terwijl de dwarsverstijvers doorlopend blijven.

Het traagheidsmoment rond de z-as moet ook voldoen:

(4) Behandeling van het uiteinde van dwarsverstijvers:

3. Verstijvers voor ondersteuning

(1) Stabiliteitsberekening:

De stabiliteit van de verstijvers voor ondersteuning wordt berekend als een drukelement dat wordt onderworpen aan vaste geconcentreerde belastingen of balksteunreacties langs zijn as. De dwarsdoorsnede A van dit drukelement omvat zowel het verstijvings- als het lijfplaatoppervlak binnen 15t_w aan elke kant van de verstijving. De berekeningslengte wordt bij benadering genomen als h0.

(2) Berekening van de druksterkte:

Het uiteinde van de verstijvers voor liggers moet worden berekend op basis van de vaste geconcentreerde belasting of oplegreactie die ze dragen. Als het uiteinde van de verstijvers vlak en strak is afgeknipt, moet de drukspanning op het eindvlak als volgt worden berekend:

waar:

• f_ce is de ontwerpwaarde voor de sterkte van de compressie van het stalen eindvlak;
• A_ce is het gebied waar de verstijvers in contact komen met de flensplaat of kolomkap.

Ontwerpstappen voor dwarsplaatverstijvers:

1. Bepaal of er dwarsbalken moeten worden geïnstalleerd;

2. Installeer de dwarsbalken en bepaal de afstand a, bs, ts;

3. Controleer de samengestelde spanningstoestand van de webplaat;

4. Controleer de ondersteunende verstijving: inclusief de lasnaad (verbinding tussen de dwarsliggers en de lijfplaat), controle van de axiale compressiestabiliteit (stabilisatie buiten het z-asvlak) en controle van de sterkte.

Voorbeeld 5-3: Controleer aan de hand van de omstandigheden en resultaten in Voorbeeld 5-2 of de hoofdligger van afbeelding 5-9(b) aan de eisen voldoet. De hoofdligger is een eenvoudig ondersteunde ligger aan beide uiteinden, gemaakt van Q235 staal en gelast met E43 serie handlaselektroden.

Oplossing:

1. Draagvermogen van de hoofdligger:

Het vereenvoudigde berekeningsdiagram van de hoofdligger wordt getoond in Figuur 5-9(a). De druk die de secundaire liggers aan beide zijden op de hoofdligger uitoefenen is 2×73,69+2×2,33=152,04 kN en de druk van de secundaire liggers aan het uiteinde van de ligger is de helft van die van de middelste secundaire ligger.

De oplegreactie van de hoofdligger is R=2×152,04=304,08 kN.

Het maximale buigmoment van de balk is M=(304,08-76,02)x5-152,04×2,5=760,2 kN.m

2. Bereken de sectiekenmerken:

A=131,2 cm², I_x=145449 cm⁴, W_x=3513,3 cm³. Het eigengewicht van de hoofdligger is 131,2×10²x7850x10-⁶x1,2=123,6 kg/m=1,211 kN/m. De factor 1,2 is om rekening te houden met de verhoogde coëfficiënt van de verstijving van de hoofdligger. De ontwerpwaarde van het buigmoment na rekening te houden met het gewicht van de hoofdligger is M=760,2+1,2×1,211×10²/8=760,2+18,2=778,4 kN-m.

Rekening houdend met de ontwerpwaarde van de reactiekracht op de steun na verrekening van het eigengewicht van de hoofdligger is R=304.08+1.2×1.211×10/2=304.08+7.27=311.3kN.

3. Sterkte controleren

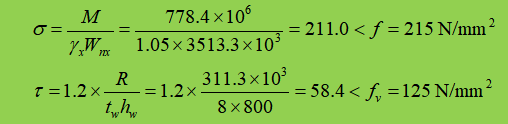
Bij de aansluiting van de secundaire ligger zijn verstevigingen aangebracht en er is geen plaatselijke drukspanning. Bovendien, omdat de schuifspanning relatief klein is, is het niet nodig om andere doorsnedespanningen te controleren.

4. Op de secundaire ligger zit een stijve plaat die de stabiliteit van de secundaire ligger garandeert en als lateraal steunpunt voor de hoofdligger kan dienen.

Op dit punt, aangezien l₁/b₁=2500/240=10,4<16, kan de algehele stabiliteit worden gegarandeerd zonder berekening.

5. Stijfheidscontrole

De totale standaardwaarde van de belasting die door de secundaire bundel wordt overgebracht, is F_T=(15.5+0.52)×7.5=120.2kN, therefore,

De totale standaardwaarde van de belasting die door de secundaire balk wordt doorgegeven, is F_Q=2.5×4.2×7.5=78.75kN, therefore,

6. Lokale stabiliteit

Flens: b/t=(120-4)/14=8,3<13, wat voldoet aan de eis van lokale stabiliteit, en γ_x kan worden genomen als 1,05; Web plaat: h₀/t_w=800/8=100, er moeten dwarsverstijvers worden aangebracht, details zijn weggelaten.

Sectie 6. Sterkte na knikken van dunne platen

1. Het concept en de analyse van sterkte na knikken van dunne platen:

Nadat de dunne plaat is geknikt, worden er dwarse trekspanningen gegenereerd in het midden van de plaat, waardoor de buigvervorming in de lengterichting van de plaat verder wordt beperkt en de plaat de verhoogde druk kan blijven weerstaan.

2. Analyse van de afschuifcapaciteit van de staalplaat rekening houdend met de sterkte na knikken:

1. Afschuifdraagcapaciteit na knik: Formule (5-94)

2. Het afschuifvermogen bestaat uit twee delen: Knikschuifkracht (kniksterkte) + trekveldschuifkracht (sterkte na knik).

3. Schuifkracht in het spanningsveld:

(1) Spanningsveldmethode (complex);

(2) Code-specificatie.

3. Analyse van het buigend draagvermogen van de staalplaat rekening houdend met de sterkte na knikken:

Gezien het feit dat de buigcapaciteit van de staalplaat iets afneemt na het knikken.

Twee aannames:

(1) Werkelijke hoogte;

(2) Symmetrie tussen de trekzone en compressiezone.

De formule voor het berekenen van de draagkracht:

4. Berekeningsformule voor liggers rekening houdend met sterkte na knikken (gelijktijdig onderworpen aan buigmoment en dwarskracht):

In de formule,

• M en V zijn de ontwerpwaarden van het buigend moment en de dwarskracht op dezelfde doorsnede van de balk
• Als V < 0,5Vu, neem dan V=0,5Vu
• Wanneer M < M_f, neem M = M_f

Dit geeft aan dat:

(1) Wanneer M op de doorsnede kleiner is dan M_f die de flens kan weerstaan, kan de webplaat de dwarskracht Vu dragen;

(2) Als V op de doorsnede minder is dan 0,5Vu, neem dan M = M_eu.

5. Ontwerp van dwarsverstijvers rekening houdend met de post-bucklingsterkte

(1) Als ondersteunende verstijvers alleen niet aan vergelijking (5.99) kunnen voldoen, moeten gepaarde dwarsverstijvers aan beide zijden van het lijf worden toegevoegd om de lengte van het knikgebied te verminderen.

(2) De dwarsdoorsnedeafmetingen van de dwarsverstijvers moeten voldoen aan de constructie-eisen voor de lijfverstijvers volgens Vergelijking 5.85.

(3) Volgens de specificaties van de staalconstructie moet de centrale dwarsverstijving worden behandeld als een axiaal drukelement en moet de stabiliteit buiten het vlak van het lijf worden berekend op basis van de axiale kracht met behulp van de volgende formule:

Wanneer de verstijver wordt onderworpen aan een geconcentreerde dwarsbelasting F, moet Ns worden verhoogd met F.

Hoofdstuk 7. Ontwerp van stalen balken

1. Ontwerp van gewalste stalen balken

Bereken de ontwerpwaarde van het maximale buigmoment M_max voor de balk op basis van de werkelijke omstandigheden.

Bepaal de vereiste doorsnedemodulus op basis van de buigsterkte en algemene stabiliteit:

Bepaal de staaldoorsnede op basis van de doorsnedetabellen.

Verificatie van de sectie:

(1) Sterkteverificatie: buiging, afschuiving, plaatselijke samendrukking en equivalente spanning.

(2) Controle van de stijfheid: controleer de verhouding tussen doorbuiging en overspanning van de balk.

(3) Controle van de algehele stabiliteit (de lokale stabiliteit van de staalsectie hoeft meestal niet gecontroleerd te worden).

(4) Pas de sectie aan op basis van de verificatieresultaten en voer de verificatie opnieuw uit totdat deze voldoet aan de ontwerpeisen.

2. Doorsnedeontwerp van samengestelde liggers

1) Bepaal de vereiste doorsnedemodulus op basis van de belastingsomstandigheden.

2) Bepaal de hoogte van de straal:

• Minimumhoogte: h_min wordt bepaald door de stijfheid van de balk.
• Maximale hoogte: h_max wordt bepaald door de architecturale ontwerpeisen.
• Economische hoogte: h_e wordt bepaald door het minimale staalverbruik.

Gekozen hoogte: h_min ≤ h ≤ h_max.

3). Bepaal dan de dikte van het lijf (ervan uitgaande dat alle dwarskrachten door het lijf worden gedragen):

Als alternatief kan de dikte van de baan worden bepaald met empirische formules:

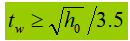
4). Bepaal de flensbreedte:

Na het bepalen van de lijfdikte wordt het flensoppervlak A_f kan worden bepaald op basis van de vereisten voor buigsterkte. Als voorbeeld nemen we een I-vormig profiel:

Eenmaal A_f bepaald is, kan b of t gekozen worden om de andere waarde te bepalen.

5). Verificatie van de sectie:

• Sterkteverificatie: buiging, afschuiving, plaatselijke compressie en equivalente spanningssterkte.
• Controle van de stijfheid: controleer de verhouding tussen doorbuiging en overspanning van de balk.
• Algehele stabiliteitsverificatie.
• Lokale stabiliteitsverificatie (flensplaat).
• Pas de sectie aan op basis van de verificatieresultaten en voer de verificatie opnieuw uit totdat het voldoet aan de ontwerpeisen.
• Bereken en schik verstijvers volgens de werkelijke omstandigheden.

6). Berekening van lassen tussen het lijf en de flens

De verbindingslas wordt voornamelijk gebruikt om weerstand te bieden aan buiging afschuivingen de afschuiving per lengte-eenheid is:

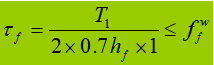
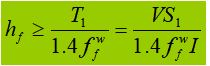
Wanneer de ligger wordt onderworpen aan een vaste geconcentreerde belasting zonder verstijvers, draagt de bovenste flenslas zowel dwarskracht T₁ en geconcentreerde kracht F. De kracht per lengte-eenheid die F genereert is V₁:

3. Wijziging van doorsnede voor gelaste samengestelde liggers

Doel: Om staal te besparen en veranderingen in het buigmoment op te vangen.

Methoden voor sectieverandering:

• Wijzig de flensbreedte.
• Wijzig de flensdikte of het aantal lagen.
• Wijzig de hoogte en dikte van de baan.

Aandachtspunten:

• Deze methode wordt alleen gebruikt voor lange overspanningen.
• De verandering van doorsnede moet geleidelijk gebeuren om ernstige spanningsconcentratie te voorkomen.
• De equivalente spanning moet worden geverifieerd.

Sectie 8. Lassen van stalen balken

1. Classificatie:

• Fabrieksmatig lassen: Uitgevoerd in gecontroleerde omgevingen voor optimale kwaliteit.
• Splitsen op locatie: Wordt gebruikt bij beperkingen in transport of handling.

2. Lasmethoden voor gewalste staalprofielen:

• Stuiklassen: Volledige penetratielassen voor maximale sterkte en naadloos uiterlijk.
• Lassen van lasplaten: Gebruikt extra platen om balksecties samen te voegen, wat flexibiliteit biedt in het ontwerp en de montage op locatie vergemakkelijkt.

3. Verbindingstechnieken voor samengestelde liggers:

• Fabrieksmatig gelast: Het lijf en de flenzen verspringen om de spanning te verdelen en de structurele integriteit te behouden.
• Splitsen op locatie: Het lijf en de flenzen worden op dezelfde sectie gelast om montage op locatie te vereenvoudigen en de bouwtijd te verkorten.

Belangrijke overwegingen:

• Splooplocaties: Plaats verbindingen strategisch op plaatsen met relatief lage buigspanning om de structurele impact te minimaliseren.
• Kwaliteitscontrole: Lassen op locatie vormt een uitdaging bij het handhaven van een constante kwaliteit vanwege omgevingsfactoren en toegankelijkheidsproblemen.
• Niet-destructief testen: Implementeer strenge inspectieprotocollen, zoals ultrasone of radiografische testen, om de integriteit van de las te garanderen.
• Overbrengen van belastingen: Ontwerp verbindingen om alle verwachte belastingen effectief over te dragen, inclusief axiale krachten, afschuifkrachten en momentkrachten.

Sectie 9. Verbinding van primaire en secundaire stalen liggers en liggersteunen

1. Primaire en secundaire stalen balkverbindingen:

• Overlappende verbindingen: Zorgen voor een uitstekende afschuiving en vereenvoudigen de montage.
  - Zittende verbindingen: De secundaire ligger rust op een plankhoek die aan de primaire ligger is gelast.
  - Boven- en onderflens flensverbindingen: Bieden verbeterde momentbestendigheid.
• Stootvoegverbindingen: Ideaal voor vlakke balkopstellingen en uniforme dieptevereisten.
  - Eindplaatverbindingen: Geboute of gelaste platen aan de uiteinden van de ligger voor nauwkeurige uitlijning.
  - Fin plaatverbindingen: Eenvoudig en voordelig voor het overbrengen van dwarslasten.

2. Typen steunbalken:

• Vlakke plaatsteunen:
  - Eenvoudig en voordelig voor gemiddelde belastingen.
  - Zorg voor een uniform draagvlak en eenvoudige installatie.
• Boogvormige steunen:
  - Belastingen gelijkmatiger verdelen, waardoor spanningsconcentraties worden verminderd.
  - Ideaal voor zware ladingen of waar roterende bewegingen worden verwacht.
• Scharnierende steunen:
  - Maak draaiende bewegingen mogelijk en pas thermische uitzetting en inkrimping toe.
  - Verminder momentoverdracht naar ondersteunende structuren.

Belangrijkste ontwerpoverwegingen:

• Draagvermogen: Kies het type ondersteuning op basis van de verwachte belastingen en structurele vereisten.
• Constructiemogelijkheden: Houd rekening met installatiegemak en mogelijkheden voor prefabricage.
• Onderhoudbaarheid: Ontwerp verbindingen en steunen om toekomstig onderhoud of aanpassingen te vergemakkelijken.
• Corrosiebescherming: Zorg voor geschikte beschermende maatregelen, vooral voor blootgestelde verbindingen.