Luchtbuigkrachtgrafiek (Amada)
In deze blogpost verkennen we de fascinerende wereld van het buigen van lucht en de krachtgrafieken die dit mogelijk maken. Doe met ons mee als we ons verdiepen in de wetenschap achter deze...
Heb je je ooit afgevraagd hoe je nauwkeurig de buigkracht berekent die nodig is voor plaatbewerking? In deze inzichtelijke blogpost verkennen we de fijne kneepjes van het berekenen van buigkracht, waarbij we putten uit de expertise van doorgewinterde werktuigbouwkundig ingenieurs. Ontdek de belangrijkste factoren die de buigkracht beïnvloeden en leer hoe je beproefde formules kunt toepassen om je metaalvormprocessen te optimaliseren. Bereid je voor om je kennis over het buigen van plaatmetaal naar nieuwe hoogten te brengen!
Op dit moment zijn de formules voor het berekenen van buigkracht die veel gebruikt worden overgenomen uit buitenlandse bronnen zonder enige informatie over hun oorsprong of toepassingsgebied.
Dit artikel geeft een systematische analyse van het afleidingsproces van de formule voor het berekenen van de buigkracht en de vereiste parameters.
Verder wordt een nieuwe benadering voor het berekenen van buigkracht geïntroduceerd om het toepassingsgebied te verbreden.
Het berekenen van de buigkracht voor plaatmetaal is essentieel voor nauwkeurige en efficiënte buigprocessen. Inzicht in deze berekeningen helpt bij het selecteren van geschikt gereedschap en het garanderen van buigingen van hoge kwaliteit. Dit hoofdstuk geeft een overzicht van de belangrijkste concepten, gereedschappen en praktische tips voor het berekenen van buigkracht bij plaatbewerking.
Buigkrachtberekeningen zijn cruciaal bij plaatbewerking om ervoor te zorgen dat de juiste hoeveelheid kracht wordt uitgeoefend tijdens het buigproces. Dit voorkomt materiaalverspilling, beschadiging van gereedschap en zorgt voor de gewenste buigkwaliteit. Nauwkeurige berekeningen helpen bij het selecteren van de juiste kantpers en gereedschappen, wat leidt tot efficiënte productie en kostenbesparingen.
De buigkracht ( F ) die nodig is om een plaat te buigen, kan worden berekend met de formule:
waar:
De inwendige straal ( R ) van de bocht wordt vaak benaderd op basis van de matrijsopening ( V ):
De matrijsopening ( V ) wordt geselecteerd op basis van de plaatdikte ( S ):
De minimale flenslengte zorgt ervoor dat het materiaal niet valt tijdens het buigproces en wordt berekend op basis van de matrijsopening en de buighoek.
In de afgelopen jaren heeft de afkantpers op grote schaal gebruikt in verschillende industrieën en heeft zijn verwerkingsmogelijkheden uitgebreid.
Ondanks de populariteit is er een gebrek aan systematische discussie over de berekening van buigkrachten.
Momenteel zijn er ongeveer twee soorten berekeningsformules voor buigkrachten die worden aanbevolen door de producthandleidingen van verschillende fabrikanten van afkantpersen.
In de formule:
De aanbevolen formule voor het berekenen van de buigkracht door de fabrikant is gebaseerd op een eerder genoemde formule.
Beide formules zijn overgenomen uit verschillende productbrochures, maar er is geen bewijs voor hun nauwkeurigheid.
Verwante rekenmachine: Kantpers tonnage calculator
Figuur 1 is een schematische weergave van de buigproces van een vel.
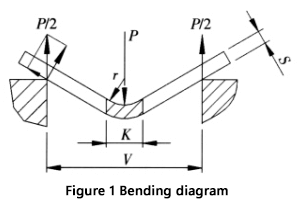
De berekening van de buigkracht en de parameters worden als volgt uitgelegd:
De aanbevolen breedte van de onderste matrijsopening (V) voor vrij buigen is 8 tot 10 keer de plaatdikte (S), met een breedte/dikteverhouding van V/S = 9.
Fabrikanten van kantpersen geven de waarden van de matrijsbreedte (V) en de binnenradius (r) van het gebogen werkstuk op in hun parametertabel voor de buigkracht. De verhouding radius/breedte is meestal r = (0,16 tot 0,17) V, en in dit geval wordt de waarde 0,16 gebruikt.
Tijdens het buigproces ondergaat het materiaal in de vervormingszone een aanzienlijke plastische vervorming, waardoor het buigt rond de middellijn.
In sommige gevallen kunnen er kleine scheurtjes ontstaan aan de buitenkant van het gebogen gebied.
De spanning in de vervormingszone, behalve in de buurt van de centrale laag, ligt dicht bij de treksterkte van het materiaal, waarbij het bovenste deel van de neutrale laag wordt samengedrukt en het onderste deel onder spanning staat.
Figuur 2 toont de doorsnede en het bijbehorende spanningsdiagram in de vervormingszone.
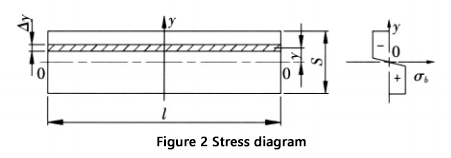
Het buigmoment in de doorsnede van de vervormingszone is:
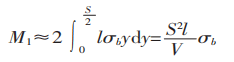
Het buigmoment geproduceerd door de buigkracht in de vervormingszone wordt weergegeven in Figuur 1.
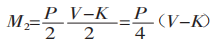
Van M1 = M2krijgen we:
Bij het buigen van een plaat met een universele mal op een buigmachine, zoals getoond in Figuur 3, worden de meeste platen gebogen tot 90°. In dit geval is K:
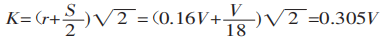
Door K in vergelijking (1) te substitueren, krijgen we:
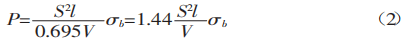
De treksterkte van gewone materialen, σb, is 450 N/mm². Deze waarde kan gebruikt worden in formule (2) om het resultaat te berekenen.
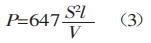
De hier verkregen formule voor het berekenen van de buigkracht komt overeen met de informatie in buitenlandse brochures.
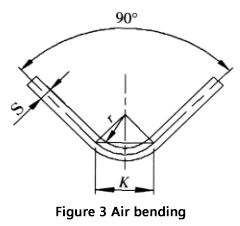
De variabelen in de formule zijn:
Zoals uit het afleidingsproces blijkt, is het bij het gebruik van formules (2) of (3) om de buigkracht te berekenen belangrijk om ervoor te zorgen dat aan twee extra voorwaarden wordt voldaan: de verhouding tussen breedte en dikte (V/S) moet gelijk zijn aan 9 en de verhouding tussen straal en breedte moet gelijk zijn aan 0,16.
Als niet aan deze voorwaarden wordt voldaan, kunnen er significante fouten optreden.
De berekening van de buigkracht kan gecompliceerd zijn als door ontwerp- of procesbeperkingen niet kan worden voldaan aan de twee aanvullende eisen (breedte-dikteverhouding V/S = 9 en straal-breedteverhouding = 0,16).
In dergelijke situaties is het raadzaam om de volgende stappen te volgen:
Deze stappen leveren een nauwkeuriger en betrouwbaarder resultaat op dan wanneer de gebruikelijke formule wordt gebruikt. Een voorbeeld om dit proces te illustreren wordt getoond in Figuur 4.
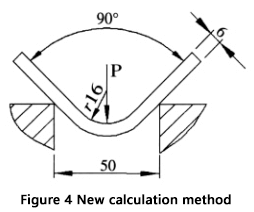
Gegeven: Plaatdikte (S) = 6 mm, Plaatlengte (l) = 4 m, Buigradius (r) = 16 mm, Breedte onderste matrijsopening (V) = 50 mm en Materiaaltreksterkte (σb) = 450N/mm².
Vraag: Hoe kunnen we de buigkracht berekenen die nodig is voor luchtbuigen?
Dit zijn de stappen:
Bereken eerst de verhouding tussen breedte en dikte en de verhouding tussen straal en breedte:
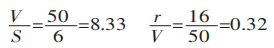
Bereken vervolgens de geprojecteerde breedte van het vervormingsgebied:
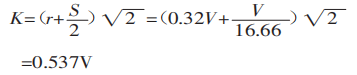
Gebruik tenslotte formule (1) om de buigkracht te berekenen:
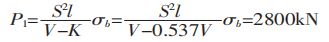
Als de gewoonlijk aanbevolen formule wordt gebruikt om de buigkracht te berekenen:
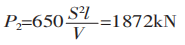
Uit P1/P2 = 1,5 kan worden afgeleid dat het verschil tussen P1 en P2 1,5 keer is.
De reden voor dit verschil is dat in dit voorbeeld de buigradius relatief groot is, wat resulteert in een groter vervormd oppervlak en dus een grotere buigkracht vereist.
De verhouding tussen straal en breedte in dit voorbeeld is 0,32, wat de eerder genoemde criteria overtreft.
Het gebruik van de standaardformule om de buigkracht te berekenen is niet geschikt voor dit scenario. De voordelen van het gebruik van de nieuwe berekeningsmethode zijn in dit voorbeeld te zien.
Daarnaast is er een online calculator beschikbaar om de buigkracht te berekenen met de nieuwe methode.
Treksterkte tabel
| Materiaal | Treksterkte | ||
|---|---|---|---|
| Amerikaanse | Europese | China | N/mm² |
| 6061 aluminium | Alu50 | LD30 | 290 |
| 5052 aluminium | Alu35 | LF2 | 303 |
| 1010 zacht staal | DC01 | 10/10F | 366 |
| A 536 -80 G 60-40-18 | GGG-40 | QT400-18 | 400 |
| A 351 G CF 8 | G-X 6CrNi 18 9 | Q235 | 450 |
| A 572 G50 | S 355 MC | Q345 | 550 |
| 304 roestvrij | Inox V2A | 0H18N9 | 586 |
| Roestvrij staal 316 | Inox V4A | 0H17N12M2 | 600 |
| 4140 Laag gelegeerd | 42 CrMo 4 | 42CrMo | 1000 |
De formules voor het berekenen van de coiningparameters zijn anders dan bij luchtbuigen.
1. Breedte van de dieve:
V = plaatmetaal dikte × 5
2. De inwendige straal wordt bepaald door de stempelpunt, die gekozen moet worden volgens de volgende formule:
Radius = plaatdikte × 0.43.
3. Benodigde kracht voor het gieten：
F(kn/m)=Dikte2×1.65×Treksterkte (N/mm2) ×4,5/Die Vee Breedte
4. De formule voor het berekenen van de minimale interne rand blijft hetzelfde:
Minimale binnenrand = stervende vee × 0.67
Sommige gereedschappen hebben een bepaalde kracht nodig om het plaatmetaal uit te rekken en de terugvering te beheersen om het gewenste profiel te verkrijgen.
Als voorbeeld nemen we joggle-gereedschappen, die twee bochten tegelijk maken met een korte afstand tussen de bocht en de tegenbocht.
Aangezien deze gereedschappen twee bochten tegelijk maken, springrug moet volledig worden geannuleerd door te munten.
De vergelijking om de benodigde kracht te berekenen is:
Tuimelgereedschap bestaat meestal uit een insteekhouder waarin de tuimelgereedschappen, gekozen in overeenstemming met de tuimelaar en de vereiste hoek, met stelschroeven worden vastgezet.
Het is belangrijk om voor aankoop technisch advies te vragen aan de fabrikant, want deze systemen kunnen alleen dun plaatstaal buigen, maximaal 2 mm, maar de maximale dikte hangt af van het type inzetstuk en kan minder dan 2 mm zijn.
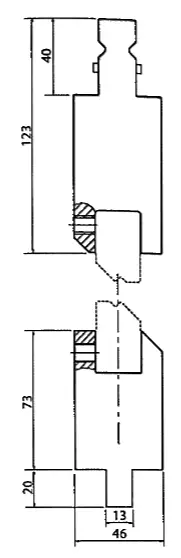
Hieronder vindt u antwoorden op een aantal veelgestelde vragen:
De treksterkte speelt een cruciale rol bij het bepalen van de benodigde buigkracht voor plaatmateriaal. Treksterkte is de maximale spanning die een materiaal kan weerstaan wanneer het wordt uitgerekt voordat het breekt. Wanneer plaatmetaal wordt gebogen, ondergaat het zowel trek- als drukspanning. Het buitenoppervlak van de bocht wordt onderworpen aan trekspanning, terwijl het binnenoppervlak een drukspanning ondergaat.
De benodigde buigkracht wordt direct beïnvloed door de treksterkte van het materiaal, omdat een hogere treksterkte betekent dat het materiaal een grotere spanning kan weerstaan zonder te bezwijken. Dit betekent dat voor materialen met een hogere treksterkte een grotere kracht nodig is om dezelfde mate van buiging te bereiken in vergelijking met materialen met een lagere treksterkte.
Om de buigkracht te berekenen wordt gekeken naar de buigspanning, die gerelateerd is aan de treksterkte. De formule voor buigspanning
Hierbij gaat het om het buigmoment (M), de afstand van de neutrale as tot de buitenste vezel (c) en het traagheidsmoment van de doorsnede (I). Het buigmoment wordt beïnvloed door de toegepaste kracht en de lengte van de hefboomarm. Ervoor zorgen dat de buigspanning de treksterkte van het materiaal niet overschrijdt is essentieel om bezwijken tijdens het buigen te voorkomen.
Samenvattend, een hogere treksterkte vereist een hogere buigkracht om plaatmetaal te buigen zonder dat het bezwijkt, wat het belang benadrukt van rekening houden met materiaaleigenschappen bij buigkrachtberekeningen.
Bij het berekenen van de buigkracht voor plaatwerk moet rekening worden gehouden met verschillende belangrijke factoren om nauwkeurige en betrouwbare resultaten te verkrijgen. De belangrijkste factoren die van invloed zijn op buigkrachtberekeningen zijn onder andere:
Materiaaleigenschappen spelen een cruciale rol, vooral treksterkte en rekgrens. Treksterkte is de maximale spanning die een materiaal kan weerstaan voordat het bezwijkt, waarbij verschillende materialen verschillende sterktes hebben. Aluminium heeft bijvoorbeeld een treksterkte van 200-300 N/mm², zacht staal (Q235) varieert van 370-500 N/mm² en roestvrij staal ligt rond 650-700 N/mm². De vloeigrens bepaalt de spanning waarbij het materiaal plastisch begint te vervormen, waarbij een hogere vloeigrens meer buigkracht vereist.
De materiaaldikte heeft een grote invloed op de buigkracht, omdat dikkere materialen meer weerstand bieden tegen vervorming, waardoor een grotere kracht nodig is. In de berekeningsformules is de materiaaldikte meestal een belangrijke variabele.
Buigradius en hoek zijn ook belangrijk. De straal van de binnenbocht, of de straal van de bocht, heeft invloed op de benodigde kracht, waarbij kleinere stralen meer kracht vereisen vanwege de hogere spanningsconcentratie. De buighoek beïnvloedt de benodigde kracht. De meeste berekeningen zijn gebaseerd op een bocht van 90 graden, maar voor andere hoeken zijn aanpassingen nodig.
De gereedschap- en matrijsconfiguratie, in het bijzonder de V-opening in de onderste matrijs, beïnvloedt de buigkracht. De breedte van het onderste matrijskanaal in de buigmachine is gerelateerd aan de materiaaldikte, en precisiebuigen kan een smallere V-opening vereisen voor dunnere materialen.
De K-factor en de positie van de neutrale as beïnvloeden ook het buigproces. De K-factor is meer direct gerelateerd aan het berekenen van buigtoeslagen en -aftrek, maar beïnvloedt het algemene buiggedrag en de benodigde kracht door te bepalen waar het materiaal niet wordt samengedrukt of uitgerekt.
Tot slot wordt voor de berekening van de buigkracht meestal een formule gebruikt waarin de treksterkte van het materiaal, de dikte en de lengte van de bocht zijn opgenomen. Een vereenvoudigde formule voor staal met een laag koolstofgehalte is bijvoorbeeld:
waarbij ( t ) de dikte in mm is en ( l ) de lengte in meters, met het resultaat in tonnen.
Door met deze factoren rekening te houden, kun je nauwkeurig de buigkracht berekenen die nodig is voor het buigen van plaatwerk, zodat je zeker weet dat de kantbank correct is ingesteld om de gewenste buiging te maken zonder materiaalbreuk of overmatige vervorming te veroorzaken.
Om de juiste instellingen voor een afkantpers te bepalen, moet je rekening houden met een aantal belangrijke factoren voor het nauwkeurig en efficiënt buigen van plaatwerk. Ten eerste moet je het materiaalsoort en de dikte bepalen, omdat deze de vereiste buigkracht aanzienlijk beïnvloeden. Verschillende metalen, zoals roestvrij staal en aluminium, hebben verschillende sterktes en elasticiteit, die van invloed zijn op de kracht die nodig is om te buigen.
Bereken vervolgens de benodigde tonnage met de formule ( P=650S²L/V ), waarbij ( P ) de buigkracht is, ( S ) de dikte van de metalen plaat en ( V ) de opening van de ondermatrijs. Houd rekening met de buiglengte en buighoek, aangezien scherpere hoeken een hogere tonnage vereisen. Zorg voor een goede ondersteuning en uitlijning van het materiaal om doorbuiging en onnauwkeurigheden te voorkomen.
Verschillende buigmethodes, zoals luchtbuigen, onderbuigen en coining, vereisen verschillende tonnages, waarbij luchtbuigen de basis is en coining ongeveer acht keer de luchtbuigtonnage vereist. Controleer of de tonnage niet hoger is dan de centrale tonnagelimiet van de afkantpers om overbelasting en mogelijke schade te voorkomen.
Kies het juiste gereedschap dat past bij het materiaal en de buigvereisten en zorg ervoor dat het gereedschap goed is uitgelijnd en geïnstalleerd. Kalibreer de machine door deze te inspecteren en schoon te maken, de achteraanslag af te stellen en de rampositie en -hoek te kalibreren. Programmeer de afkantpers volgens de berekende tonnage en buigparameters en voer een testrun uit op afvalmateriaal om de instellingen te fine-tunen en de gewenste resultaten te garanderen.
Door deze stappen te volgen, kun je nauwkeurig de juiste instellingen voor je afkantpers bepalen, wat leidt tot nauwkeurig en efficiënt buigen van plaatwerk.
De gegeven formules en stappen voor het berekenen van de buigkracht zijn niet alleen geschikt voor het hoekbuigen van een plaat, maar ook voor boogbuigen (wat technisch gezien moet worden aangeduid als hoekbuigen met een grote buigradius).
Het is cruciaal om in gedachten te houden dat het vormen van een boogvorm een uniek matrijsontwerp vereist.
Bij het projecteren van het vervormingsgebied moet de berekening worden gebaseerd op de procesparameters die tijdens het proces zijn vastgesteld en die niet met een enkele formule kunnen worden bepaald.
In een specifieke fabriek voor ijzertorens hebben we met succes een cilinder met een wanddikte van 12 mm, een diameter van 800 mm en een lengte van 16 m gebogen met een pers van 28000 kN. remmachine en een ronde mal.
De in dit artikel beschreven methode werd gebruikt om de buigkracht te bepalen en leverde bevredigende resultaten op bij het ontwerpen van een mal voor een boogvorm.
Verder lezen:
Als oprichter van MachineMFG heb ik meer dan tien jaar van mijn carrière gewijd aan de metaalbewerkingsindustrie. Door mijn uitgebreide ervaring ben ik een expert geworden op het gebied van plaatbewerking, verspaning, werktuigbouwkunde en gereedschapsmachines voor metalen. Ik denk, lees en schrijf voortdurend over deze onderwerpen en streef er voortdurend naar om voorop te blijven lopen in mijn vakgebied. Laat mijn kennis en expertise een aanwinst zijn voor uw bedrijf.
NL 
EN 
AR 
DE 
ES 
FR 
ID 
IT 
JA 
PT 
PT_BR 
RU 
KO 
TR