Hoe voorspellen ingenieurs wanneer een materiaal zal bezwijken onder herhaalde spanning? Dit artikel introduceert de S-N curve, een belangrijk hulpmiddel bij vermoeiingsanalyse. Je leert hoe gemiddelde spanning, multiaxiale spanningsconversie en onregelmatige spanning worden behandeld om de vermoeiingslevensduur van materialen te voorspellen. Inzicht in deze concepten kan helpen bij het ontwerpen van duurzamere en betrouwbaardere componenten. Lees verder om de fijne kneepjes van vermoeiingsanalyse te ontdekken en de levensduur van uw engineeringprojecten te garanderen.
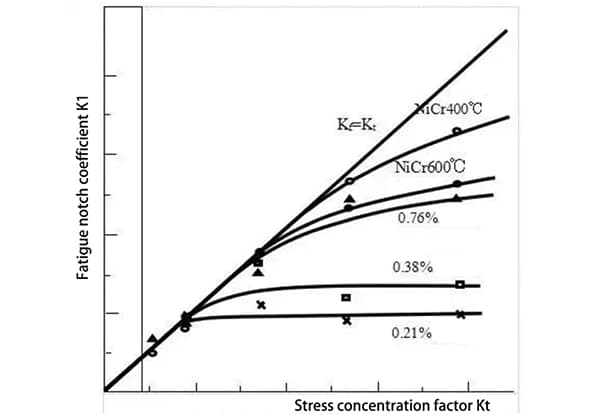
De vermoeiingseigenschappen van materialen worden typisch uitgedrukt door middel van éénassige spanningscycli, bekend als S-N krommen. Het is belangrijk op te merken dat vermoeiingstheorie gebaseerd op breukmechanica in deze context niet wordt beschouwd.
De spanningsvariatie in de tijd volgt vaak een regelmatig patroon, zoals een sinusgolf, blokgolf of puls. De invloed van de gemiddelde spanning op de vermoeiingsprestatie wordt echter vaak verwaarloosd (d.w.z. de invloed van r=Smin/Smax ≠ -1).
In werkelijkheid is de spanningstoestand gewoonlijk multiaxiaal, met een onregelmatige spanningsvariatie en r≠-1. De overeenkomst tussen werkelijke spanning en vermoeiingsprestatie gemeten in het lab, met regelmatige spanningsvariatie, eenassige spanning en r=1, vormt de basis voor vermoeiingsanalyse.
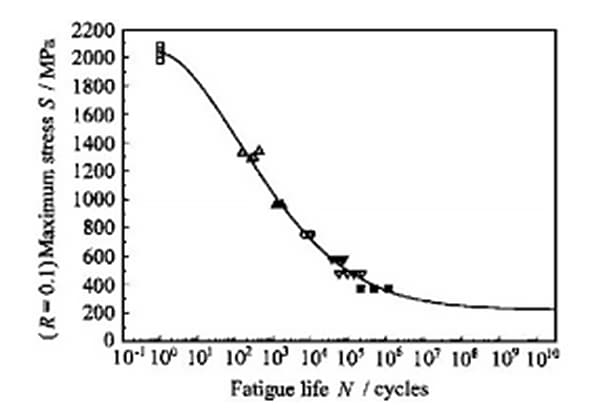
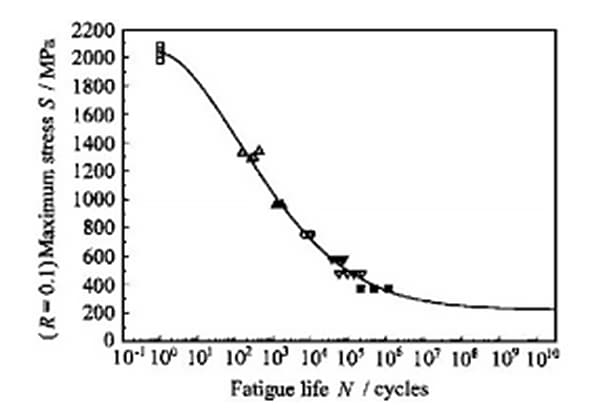
Als er S-N-curves beschikbaar zijn voor verschillende r-waarden, wordt meestal de interpolatiemethode gebruikt om de S-N-curve voor onbekende r-waarden te bepalen.
In gevallen waar alleen een S-N curve met r=-1 beschikbaar is, kan de volgende formule gebruikt worden om de equivalente spanning te berekenen. Deze formule rekent de eenassige spanning van r≠-1 om naar de eenassige spanning wanneer r=-1, die bekend staat als de equivalente spanning:
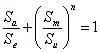
Waar Sa de halve spanningsamplitude, Se de gewenste equivalente spanning is, Sm de gemiddelde spanning is, en verschillende waarden van Su en n vormen verschillende theorieën:
De volgende spanningsopties zijn beschikbaar om het type spanning te bepalen dat gebruikt wordt voor de transformatie: Von Mises equivalente spanning, maximale schuifspanning, maximale hoofdspanning, of een specifieke spanningscomponent (zoals Sx, Syz, etc.).
Soms wordt ook Mises-spanning met een teken gebruikt, waarbij de grootte onveranderd blijft. Het teken komt overeen met het teken van de maximale hoofdspanning. Een voordeel van deze methode is dat er rekening gehouden kan worden met trek- of compressie-effecten, die tot uiting komen in de gemiddelde spanning of r.
Vergelijkbaar met de sterktetheorieVon Mises equivalente spanning en maximale afschuifspanning conversie zijn geschikt voor materialen met hoge ductiliteit, terwijl de maximale hoofdspanning conversie geschikt is voor brosse materialen.
De equivalente eenassige spanningstijdcurve van onregelmatig hoog en laag wordt geanalyseerd om een reeks eenvoudige spanningscycli (Sa, Sm) en hun overeenkomstige tijden.
Tellingen en statistieken kunnen worden verkregen met verschillende methoden, waaronder de padafhankelijke methode en de padonafhankelijke methode.
De padcorrelatiemethode, de meest gebruikte methode om regenhoeveelheden te tellen, wordt toegepast om het telproces te voltooien. Het algoritme en het principe worden uitgelegd in "Downing, S., Society, D. (1982) Simplified rain flow counting algorithms. Int J Fatigue, 4, 31 - 40".
Na de regenstroombehandeling wordt de onregelmatige spanningstijdcurve omgezet in een reeks eenvoudige cycli (Sa, Smen niwaarbij ni het aantal cycli is).
Deze methode maakt het mogelijk om de theorie over schadeaccumulatie (Miner-criterium) toe te passen om te berekenen en te analyseren: Som (ni/Ni), waarbij Ni de levensduur is die overeenkomt met de stresscyclus (rekening houdend met Sa, Smzie hierboven).
Deze techniek wordt vaak gebruikt om de veiligheidsfactor te meten na een bepaald aantal cycli of de overeenkomstige levensduur van een specifieke complexe spanningscyclus.
Op dit moment is commerciële software voor vermoeiingsanalyse meestal gebaseerd op het bovengenoemde proces.
Er moet echter worden opgemerkt dat vermoeiingsanalyse een empirische analyse is en dat er momenteel geen volwassen en volledige theorie bestaat.
Er bestaan verschillende perspectieven voor de omzetting van multiaxiale spanning naar eenassige spanning.
De Von Mises spanning, bijvoorbeeld, is een grootheid van de spanningsafmeting gebaseerd op het idee van de specifieke energie van vormverandering.
Het gebruik van de begrippen positief en negatief of spanning en compressie is een onnauwkeurige methode die niet wordt aanbevolen.
De keuze van het spanningstype hangt af van de mogelijke trend van scheuren in materialen of constructies om te bepalen welk spanningstype de primaire factor is. falen door vermoeidheid.
De technische praktijk heeft aangetoond dat staal met een goede plasticiteit vaak beschadigd raakt door herhaalde dynamische belasting van de hoofdspanning in gevallen van falen door vermoeidheid.
Supplement voor de behandeling van het gemiddelde stresseffect:
"Als er S-N-curves onder verschillende R-waarden zijn, wordt meestal de interpolatiemethode gebruikt om de S-N-curve onder onbekende R-waarden te bepalen."
Dit is slechts één methode, die handig is als er meerdere spanningen te controleren zijn. Deze methode kan echter omslachtig zijn als er slechts één spanningslevensduur gecontroleerd moet worden.
Een andere methode is om de equivalente halve spanningsamplitude te bepalen onder de voorwaarde van R = -1 en dan de S-N-curve direct toe te passen.
Wanneer er een gemiddelde spanning is, kan de S-N kromme niet direct worden gebruikt. Gebruik in plaats daarvan de GOODMAN CURVE of de aangepaste GOODMAN CURVE.
Als oprichter van MachineMFG heb ik meer dan tien jaar van mijn carrière gewijd aan de metaalbewerkingsindustrie. Door mijn uitgebreide ervaring ben ik een expert geworden op het gebied van plaatbewerking, verspaning, werktuigbouwkunde en gereedschapsmachines voor metalen. Ik denk, lees en schrijf voortdurend over deze onderwerpen en streef er voortdurend naar om voorop te blijven lopen in mijn vakgebied. Laat mijn kennis en expertise een aanwinst zijn voor uw bedrijf.
NL 
EN 
AR 
DE 
ES 
FR 
ID 
IT 
JA 
PT 
PT_BR 
RU 
KO 
TR