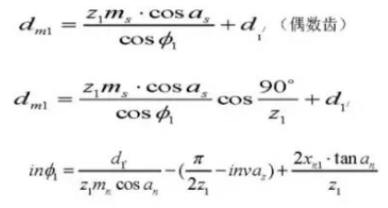Heb je je ooit afgevraagd wat de fascinerende wereld van tandwielen is? In deze blogpost verkennen we de geschiedenis, soorten en terminologie van deze essentiële mechanische onderdelen. Verdiep je samen met ons in de fijne kneepjes van tandwielen en laat je leiden door de expertise van een doorgewinterde werktuigbouwkundig ingenieur. Ontdek hoe tandwielen zich door de eeuwen heen hebben ontwikkeld en leer meer over hun cruciale rol in moderne machines.
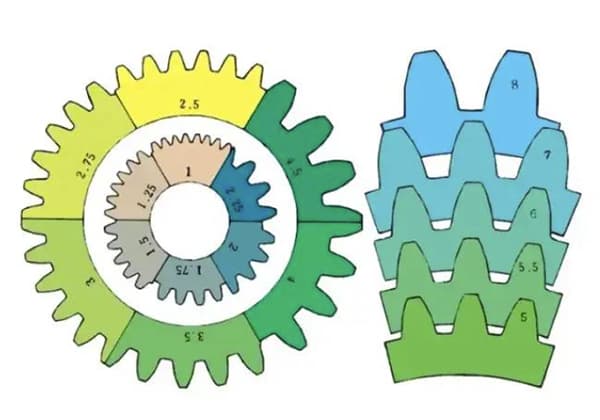
Een tandwiel is een mechanisch precisieonderdeel met tanden dat ontworpen is om in elkaar te grijpen met andere tandwielen of getande onderdelen. Het is een fundamenteel element in krachtoverbrengingssystemen dat draaisnelheid en koppel tussen assen omzet. Tandwielen worden gekenmerkt door hun ronde vorm met gelijkmatig verspreide tanden langs de omtrek, meestal volgens een omgekruld profiel voor een optimale aangrijping.
De toepassing van tandwielen in mechanische transmissie en in het bredere gebied van werktuigbouwkunde is uitzonderlijk divers en cruciaal. Ze zijn een integraal onderdeel van een breed scala aan machines en apparaten, van eenvoudig handgereedschap tot complexe industriële apparatuur en krachtige voertuigen. Tandwielen maken een nauwkeurige regeling van snelheid, richting en kracht in mechanische systemen mogelijk, waardoor ze onmisbaar zijn in aandrijflijnen, reductoren, differentiëlen en talloze andere mechanische assemblages.
De veelzijdigheid van tandwielen komt voort uit het feit dat ze gemaakt kunnen worden in verschillende maten, materialen en configuraties, waaronder rechte, schuine, conische en wormwieloverbrengingen, elk geschikt voor specifieke toepassingen en prestatievereisten. Naarmate de technologie voortschrijdt, blijven het ontwerp en de productie van tandwielen zich ontwikkelen, waarbij nieuwe materialen, productietechnieken en optimalisatiemethoden worden gebruikt om de efficiëntie, duurzaamheid en geluidsreductie van mechanische systemen te verbeteren.
Al in 350 voor Christus schreef de beroemde Griekse filosoof Aristoteles over tandwielen in zijn literatuur.
Rond 250 voor Christus beschreef de wiskundige Archimedes in zijn literatuur ook het gebruik van een turbine en een wormwiel in een takel.
Versnellingen van eeuwen voor Christus zijn nog steeds bewaard in de Ktesibios waterklok in Irak.

De geschiedenis van tandwielen in China gaat terug tot de oudheid en kent een lange en uitgebreide geschiedenis. Volgens historische gegevens werden tandwielen al in 400-200 voor Christus gebruikt in het oude China.
De bronzen tandwielen die in de provincie Shanxi zijn opgegraven, zijn de oudste die tot nu toe ter wereld zijn ontdekt. Geleide auto's die de verworvenheden van de oude wetenschap en technologie weerspiegelden, waren mechanische apparaten die draaiden rond tandwielmechanismen.
Tijdens de Italiaanse Renaissance in de tweede helft van de 15e eeuw drukte het beroemde allround genie Leonardo da Vinci niet alleen een onuitwisbare stempel op culturele en artistieke aspecten, maar leverde hij ook belangrijke bijdragen aan de geschiedenis van de tandwieltechnologie.
Na meer dan 500 jaar hebben de huidige tandwielen nog steeds de prototypeschetsen uit die tijd.
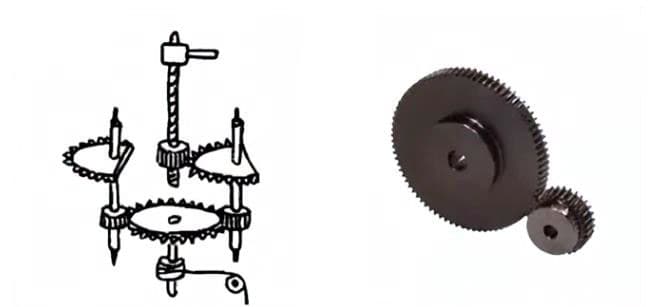
(1) Tandwiel
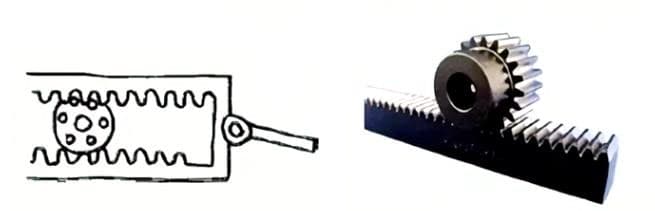
(2) Tandheugel en rondsel
(3) Schuine vertanding met gekruiste assen

(4) Kegelwiel
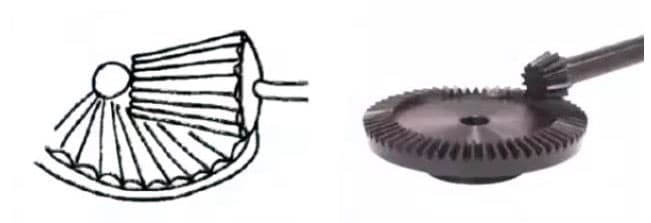
(5) Hypoïde kegelwiel met hoge overbrengingsverhouding
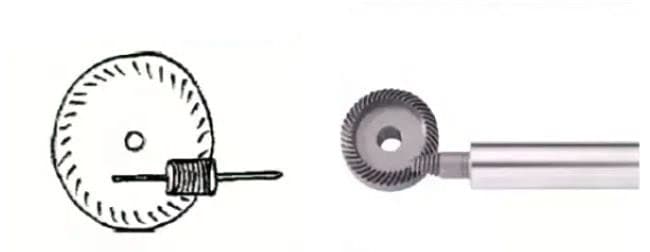
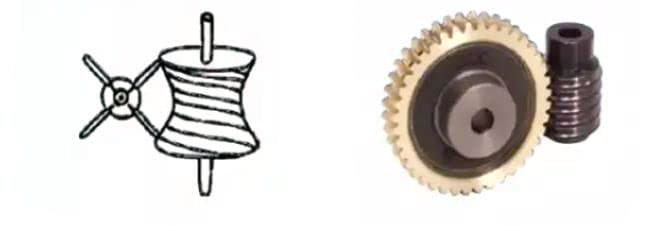
(6) Wormwiel
Pas aan het einde van de 17e eeuw begon men de tandvorm van het wiel te bestuderen, waarmee beweging nauwkeurig kon worden overgebracht. Na de industriële revolutie in Europa in de 18e eeuw werd de toepassing van tandwieloverbrenging steeds wijder verspreid.
Eerst werd de cycloïdale tandwieloverbrenging ontwikkeld, gevolgd door de evolvente tandwieloverbrenging. Aan het begin van de 20e eeuw was de evolvente vertanding dominant in zijn toepassing. Later werden tandwielen zoals de rechte tandwieloverbrenging, de boogtandwieloverbrenging, de conische tandwieloverbrenging en de scheve tandwieloverbrenging ontwikkeld.
Tegenwoordig heeft de moderne tandwieltechnologie grote vooruitgang geboekt. Tandwielmodules variëren van 0,004 tot 100 millimeter, de diameter van het tandwiel kan variëren van 1 millimeter tot 150 meter. De krachtoverbrenging Het vermogen kan oplopen tot 100.000 kilowatt en de rotatiesnelheid kan oplopen tot 100.000 omwentelingen per minuut. De hoogste omtreksnelheid kan oplopen tot 300 meter per seconde.
Internationaal ontwikkelen tandwielkasten voor krachtoverbrenging zich in de richting van miniaturisatie, hoge snelheid en standaardisatie. Enkele trends in het ontwerp van tandwielen zijn de toepassing van speciale tandwielen, de ontwikkeling van planetaire tandwielkasten en het onderzoek naar en de ontwikkeling van tandwielsystemen met weinig trillingen en geluid.
Er zijn verschillende soorten tandwielen en de meest gebruikelijke classificatiemethode is gebaseerd op de as van het tandwiel.
Over het algemeen worden tandwielen ingedeeld in drie types: parallelle as, kruisende as en schuine as.
Parallelas tandwielen: zoals rechte tandwielen, schuine tandwielen, interne tandwielen, tandheugels en schuine tandheugels.
Itandwielen met snijdende as: zoals rechte conische tandwielen, spiraalconische tandwielen, conische tandwielen met nul graden, enz.
Tandwielen met schuine as: inclusief schuine tandwielen met gekruiste assen, wormwielen, conische tandwielen, enz.
| Type versnelling | Type vistuig | Transmissie-efficiëntie (%) | 3D grafische weergave |
Parallelas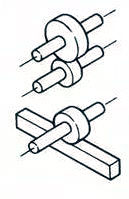 | Tandwielen | 98.0-99.5 | 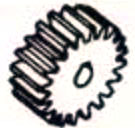 |
| Rechte tandwielen |  | ||
| Rekken,Spiraalvormige rekken |  | ||
| Intemal tandwielen | 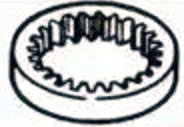 | ||
Snijas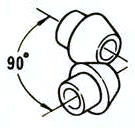 | Verstek tandwielen | 98.0-99.0 |  |
| Rechte conische tandwielen |  | ||
| Spiraal kegeltandwielen |  | ||
Schuine as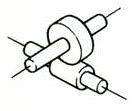 | Schroeftandwielen | 70.0-95.0 |  |
| Wormen | 30.0-90.0 |  | |
| Wormwielen | 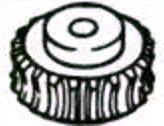 |
Het rendement in de bovenstaande tabel is het overbrengingsrendement, waarin de verliezen van lagers en bewegende smering niet zijn opgenomen. De maaswijdte van parallelle en kruisende tandwielparen is in principe rollend en het relatieve glijden is erg klein, dus het rendement is hoog.
Het in elkaar schuiven van tandwielparen met een versprongen as, zoals spiraaltandwielen en wormwielen, heeft een aanzienlijke invloed op de wrijving, omdat de krachtoverbrenging plaatsvindt door relatief glijden, waardoor de transmissie-efficiëntie lager is dan bij andere tandwielen.
De efficiëntie van tandwielen verwijst naar de transmissie-efficiëntie van tandwielen in hun normale assemblagetoestand.
Bij onjuiste installatie, vooral wanneer de afstand van de conische tandwielassemblage onjuist is en een fout veroorzaakt bij de kruising van dezelfde conische tand, zal de efficiëntie aanzienlijk afnemen.
1. Tandwielen
Cilindrische tandwielen waarbij de tandlijnen en axiale lijnen parallel zijn. Ze worden veel gebruikt in de krachtoverbrenging omdat ze gemakkelijk te bewerken zijn.
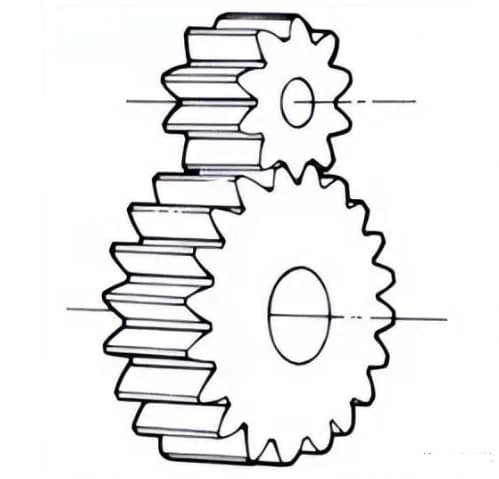
2. Rek
Een tandwiel met rechte vertanding dat in tandwielen met rechte vertanding past. Het kan gezien worden als een speciaal geval waarbij de steekdiameter van het tandwiel oneindig groot wordt.
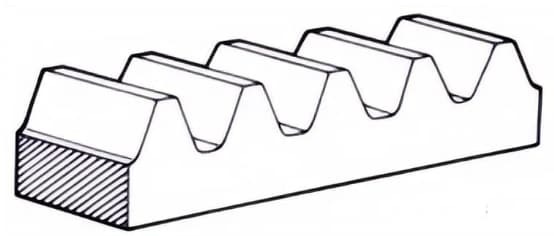
3. Interne tandwielen
Tandwielen met tanden aan de binnenkant van een ring die in elkaar grijpen met rechte tandwielen. Ze worden voornamelijk gebruikt in toepassingen zoals planetaire tandwieltransmissiemechanismen en tandwielkoppelingen.
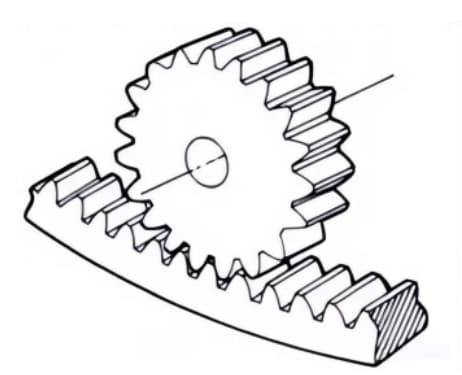
4. Spiraalvormige tandwielen
Cilindrische tandwielen met tandlijnen in de vorm van een helix. Ze worden veel gebruikt vanwege hun hoge sterkte en soepele werking, in vergelijking met rechte tandwielen. Ze genereren axiale stuwkracht tijdens de transmissie.
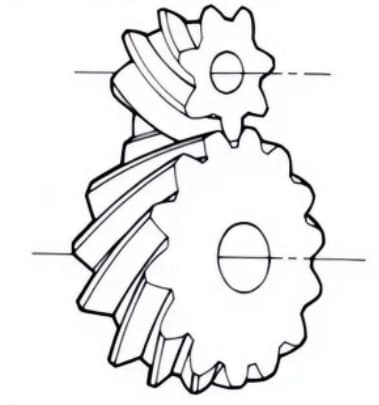
5. Spiraalvormig rek
Een tandheugel die in een spiraalvormig tandwiel past. Dit komt overeen met het geval waarbij de steekdiameter van het rechte tandwiel oneindig groot wordt.
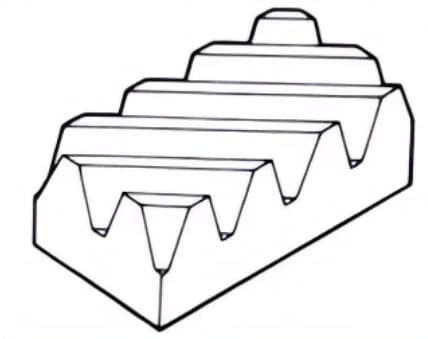
6. Visgraat tandwielen
Tandwielen die bestaan uit twee spiraalvormige tandwielen met tegengestelde spiraalhoeken. Ze hebben het voordeel dat ze geen axiale stuwkracht genereren.
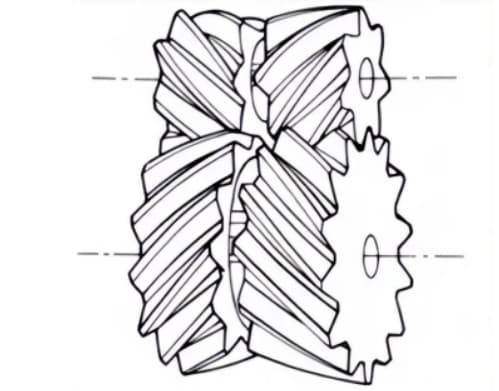
1. Rechte kegelwieloverbrengingen
Kegeltandwielen met tandlijnen die evenwijdig zijn aan de generatrix van de kegel. Ze zijn relatief eenvoudig te produceren in vergelijking met andere soorten conische tandwielen.
Daarom worden ze veel gebruikt in conische tandwieltoepassingen voor krachtoverbrenging.
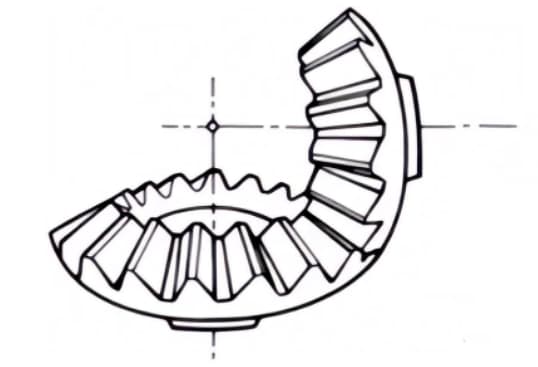
2. Spiraal kegelwieloverbrengingen
Kegeltandwielen met gebogen tandlijnen en een spiraalhoek. Hoewel ze moeilijker te produceren zijn dan rechte kegeltandwielen, worden ze veel gebruikt als tandwielen met hoge sterkte en weinig geluid.
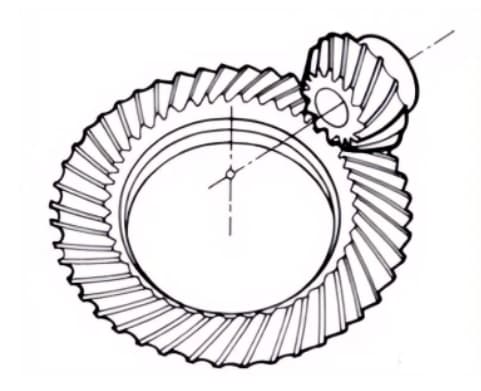
3. Nul kegelwieloverbrengingen
Gebogen conische tandwielen met een spiraalhoek van nul graden. Ze hebben de kenmerken van zowel rechte als spiraalkegeltandwielen, waarbij het tandoppervlak aan dezelfde krachtsituatie wordt blootgesteld als bij rechte kegeltandwielen.
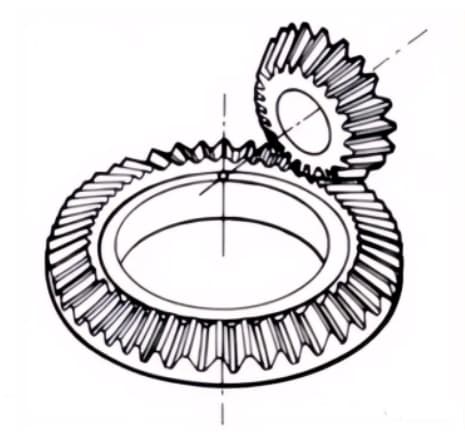
1. Wormwielpaar
De term "wormpaar" verwijst naar een combinatie van een worm en een wormwiel dat ermee in elkaar grijpt. Het grootste kenmerk van het wormpaar is dat een grote overbrengingsverhouding kan worden verkregen met slechts één paar en dat ze stil werken. Hun lage efficiëntie is echter een nadeel.
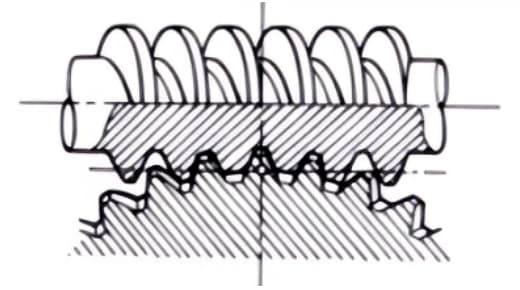
2. Kegelwiel en wormwielpaar
Een term die wordt gebruikt wanneer cilindrische wormparen worden gebruikt voor overbrenging tussen versprongen assen. Ze kunnen worden gebruikt in het geval van schuine tandwielparen of tussen schuine en rechte tandwielparen. Hoewel ze soepel werken, zijn ze alleen geschikt voor gebruik onder lichte belasting.
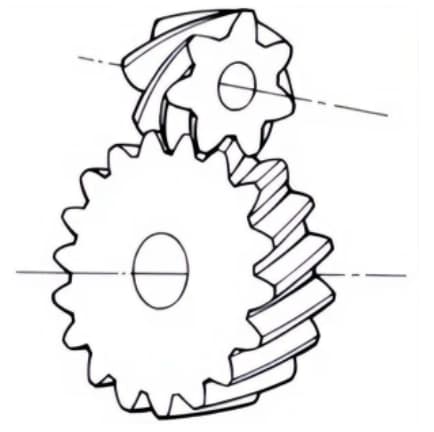
1. Gezichtsversnellingen
Schijfvormige tandwielen die kunnen samenwerken met rechte of schuine tandwielen. Ze worden gebruikt voor de overdracht tussen orthogonale assen en versprongen assen.
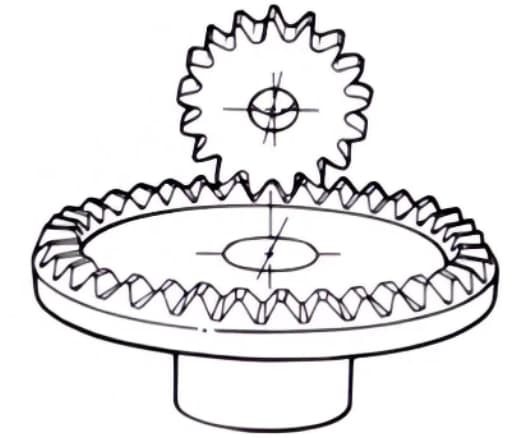
2. Zandloper wormwielpaar
De term "zandloper wormpaar" verwijst naar een combinatie van een zandloperworm en een wormwiel dat ermee in elkaar grijpt. Hoewel ze moeilijker te maken zijn dan cilindrische wormparen, kunnen ze zware lasten overbrengen.
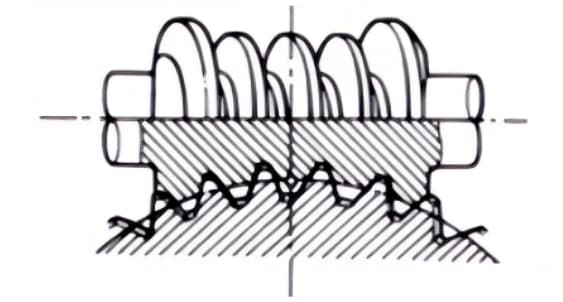
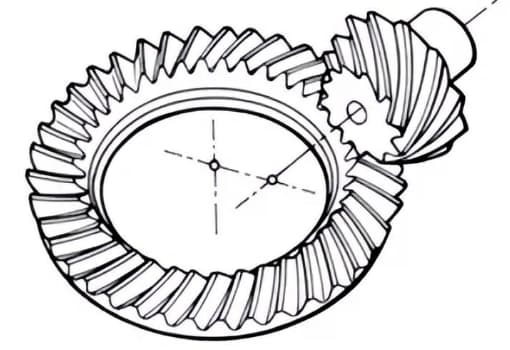
3. Hypoïde tandwielen
Conische tandwielen die worden gebruikt voor de overbrenging tussen versprongen assen. De grotere en kleinere tandwielen worden excentrisch bewerkt, net als bij conische spiraaltandwielen. Het maasprincipe is erg complex.
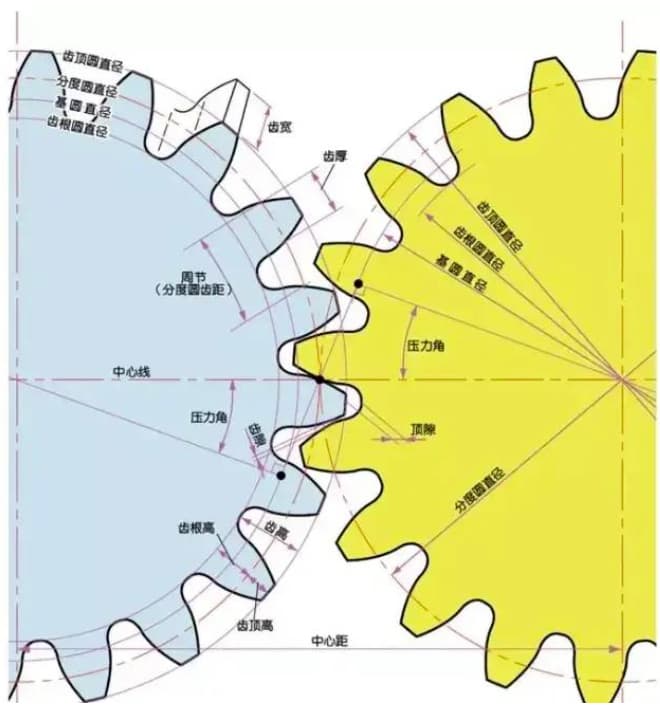
Tandwielen hebben verschillende terminologie en presentatiemethoden. Om het begrip van tandwielen te vergroten, volgen hier enkele veelgebruikte basisterminologieën voor tandwielen.
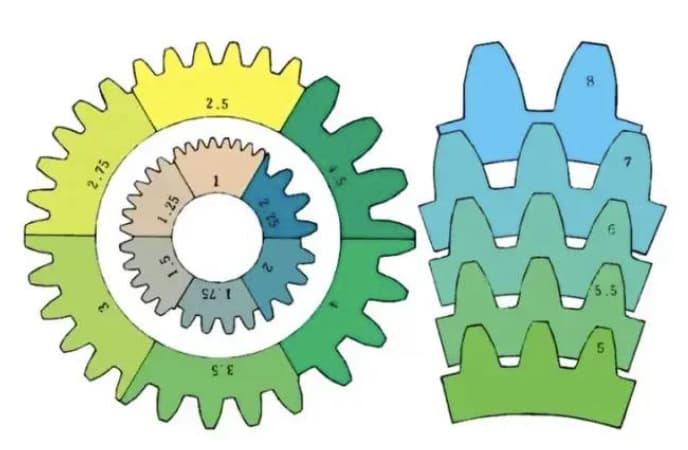
m1, m3, m8... worden respectievelijk module 1, module 3 en module 8 genoemd. De module wordt wereldwijd universeel gebruikt om de grootte van het tandwiel aan te geven, waarbij het symbool m (module) en getallen (millimeters) worden gebruikt om de grootte van de tanden weer te geven.
Hoe groter het getal, hoe groter de versnelling.
In landen die imperiale eenheden gebruiken, zoals de Verenigde Staten, wordt de grootte van de tanden aangegeven met het symbool DP (diametrale steek) en getallen (het aantal tanden voor een tandwiel met een steekdiameter van 1 inch).
Bijvoorbeeld: DP24, DP8 enz. Er is ook een vergelijkende en speciale methode om de grootte van tanden aan te geven met het symbool CP (cirkelvormige steek) en getallen (millimeters), zoals CP5, CP10.
De spoed (p) kan worden verkregen door de modulus te vermenigvuldigen met pi. De steek is de lengte tussen aangrenzende tanden.
De formule is: p= pi x m
Vergelijking van tandgrootte voor verschillende modules:
De drukhoek is een parameter die de vorm van de tandwieltanden bepaalt. Hij verwijst naar de helling van het tandwieloppervlak en wordt meestal ingesteld op 20 graden (α).
Vroeger waren tandwielen met een drukhoek van 14,5 graden gebruikelijk.
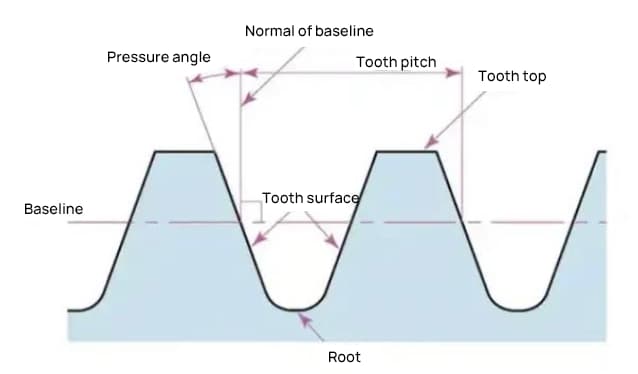
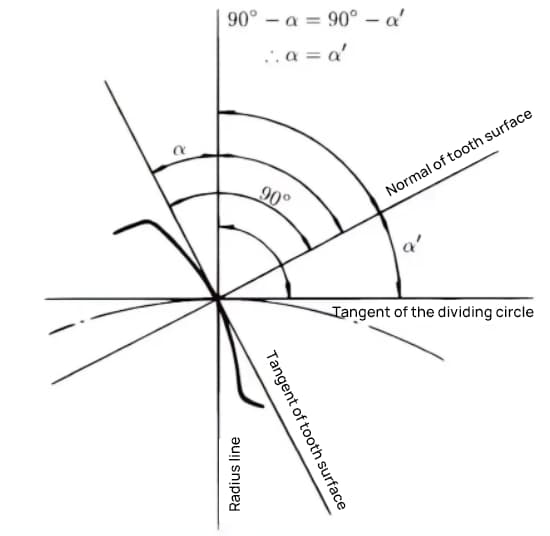
De drukhoek is de hoek die gevormd wordt tussen de straal en de raaklijn van de tandvorm op een specifiek punt op het tandoppervlak (meestal het knooppunt). Zoals in de afbeelding te zien is, is α de drukhoek. α' is ook een drukhoek omdat α' = α.
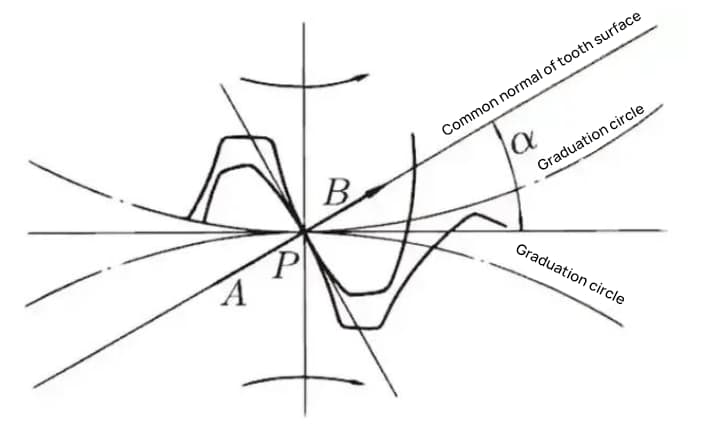
Als de meshing-toestand van tandwiel A en tandwiel B wordt bekeken vanaf het knooppunt, duwt tandwiel A tandwiel B vanaf het knooppunt. Op dat moment werkt de drijvende kracht op de gemeenschappelijke normaal van tandwiel A en tandwiel B. Met andere woorden, de gemeenschappelijke normaal is de richting van de kracht en de richting van het druklager, waarbij α de drukhoek is.
De module (m), drukhoek (α) en het aantal tanden (z) zijn de drie basisparameters van een tandwiel. Op basis hiervan wordt elk onderdeel van het tandwiel berekend in termen van grootte.
De hoogte van een tandwieltand wordt bepaald door de module (m).
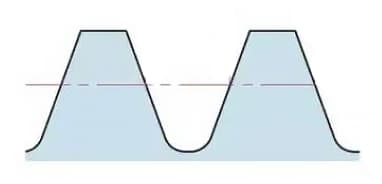
De volledige tandhoogte is h=2,25m (= addendumhoogte + deeddumhoogte).
De addendumhoogte (ha) is de hoogte van de punt van de tandwieltand tot de steekcirkel. ha=1m.
De deeddumhoogte (hf) is de hoogte vanaf de wortel van de tandwieltand tot de steekcirkel. hf=1,25m.
De referentie voor de dikte van de tandwieltand (s) is de helft van de steek. s=πm/2.
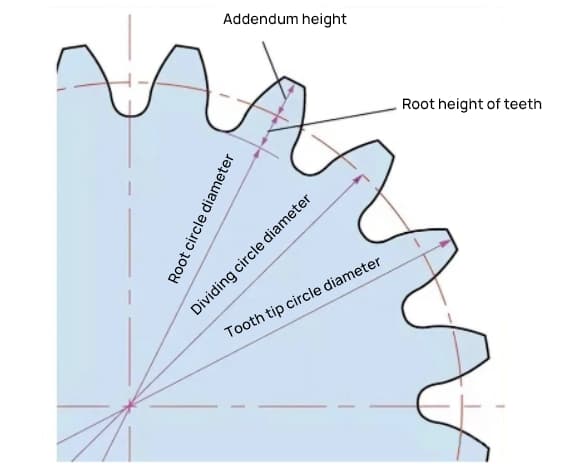
De parameter die de grootte van een tandwiel bepaalt, is de steekcirkeldiameter (d). Op basis van de steekcirkel kunnen de spoed, dikte, hoogte, addendumhoogte en deeddumhoogte van het tandwiel worden bepaald.
De steekcirkeldiameter is d=zm.
De diameter van de toegevoegde cirkel is da=d+2m.
De deeddumcirkeldiameter is df=d-2,5m.
De steekcirkel is niet direct zichtbaar op het tandwiel zelf, omdat het een aangenomen cirkel is die wordt gebruikt om de grootte van het tandwiel te bepalen.
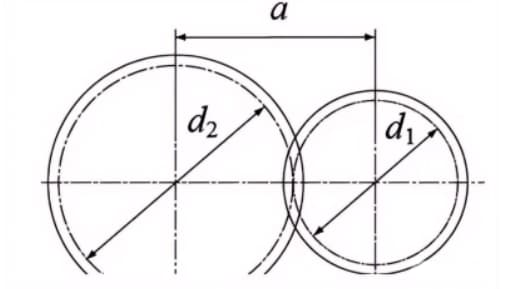
Als de steekcirkels van een tandwielpaar tangentieel in elkaar grijpen, is de centrum afstand is de helft van de som van de steekcirkeldiameters.
Centrumafstand a=(d1+d2)/2
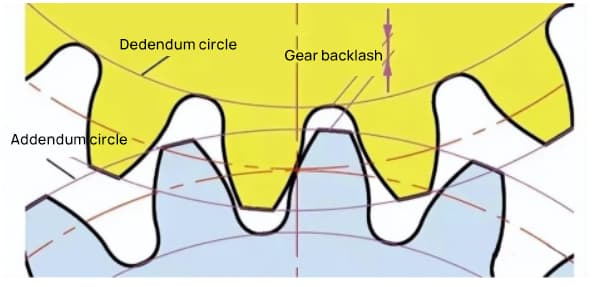
Speling is een belangrijke factor voor het soepel in elkaar grijpen van tandwielen tijdens het inschakelen. Het is de ruimte tussen de tandoppervlakken wanneer een paar tandwielen in elkaar grijpen.
Er is ook speling in de richting van de tandwielhoogte. Deze speling staat bekend als axiale speling of speling (c). De speling (c) is het verschil tussen de wortelcirkeldiameter van een tandwiel en de tipcirkeldiameter van het bijbehorende tandwiel.
Vrije ruimte c=1,25m-1m=0,25m
Een tandwiel waarvan de tanden spiraalvormig gedraaid zijn na een tandwiel, wordt een schuin tandwiel genoemd. De meeste geometrische berekeningen voor een rechte vertanding zijn ook van toepassing op een rechte vertanding. Er zijn twee soorten rechte tandwielen op basis van hun referentievlakken:
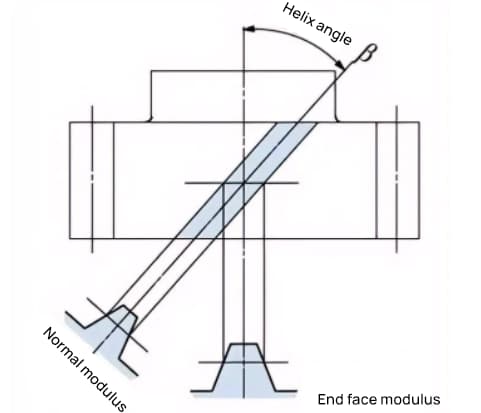
Voor schuine tandwielen, zoals rechte tandwielen en cycloïdale tandwielen, waarvan de tanden spiraalvormig zijn, liggen de helixrichting en de maaswijdte vast.
Helixrichting verwijst naar wanneer de as van het tandwiel naar boven en naar beneden wijst, de richting van de tanden naar rechtsboven als "rechts" en naar linksboven als "links" als je van voren kijkt. Het in elkaar grijpen van verschillende soorten tandwielen wordt hieronder getoond.

Als tanden met gelijke tussenruimte alleen aan de buitenrand van het wrijvingswiel worden verdeeld, van uitsteeksels worden voorzien en dan met elkaar worden vermaasd en gedraaid, kunnen de volgende problemen ontstaan:
Als de tandwieloverbrenging zowel stil als soepel moet zijn, worden omgekrulde krommingen gebruikt.
Een omgekrulde kromme is een kromme die wordt verkregen door een draad met een potlood op de buitenste omtrek van een cilinder te winden en de draad geleidelijk los te laten in gespannen toestand.
De door het potlood getrokken kromme is de omgekrulde kromme, en de buitenste omtrek van de cilinder wordt de basiscirkel genoemd.
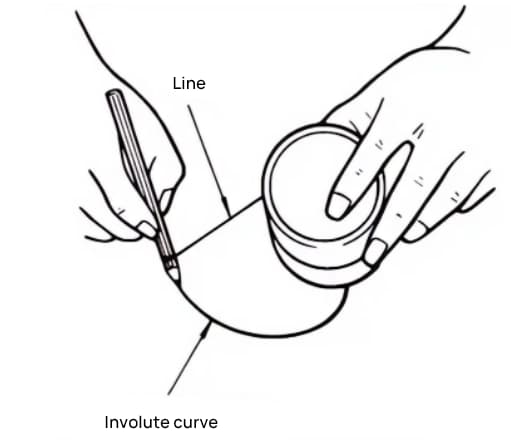
Verdeel de cilinder in 8 gelijke delen en bind er 8 potloden aan vast om 8 omgekrulde krommen te tekenen. Wikkel de draden vervolgens in de tegenovergestelde richting en teken nog eens 8 krommingen met dezelfde methode. Dit is een tandwiel met 8 tanden met omgekrulde krommingen als tandprofiel.
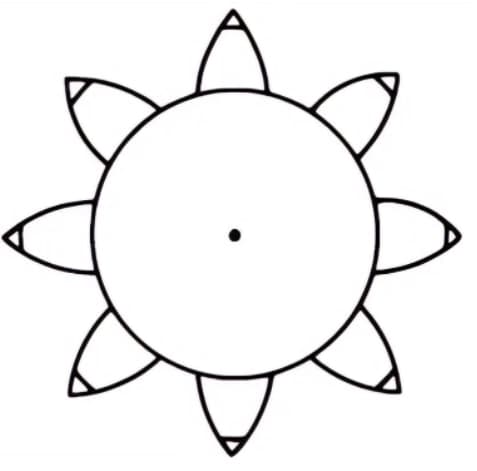
De voordelen van spiraalvormige tandwielen zijn onder andere de mogelijkheid om een constante snelheidsverhouding over te brengen, een soepele werking door het geleidelijk veranderende contactpatroon en een lage gevoeligheid voor variaties in de hartafstand.
De basiscirkel is de basiscirkel die het omgekrulde tandprofiel vormt. De steekcirkel is de referentiecirkel die de grootte van het tandwiel bepaalt. De basiscirkel en steekcirkel zijn belangrijke geometrische afmetingen van tandwielen.
Het omgekrulde tandprofiel is een kromming gevormd aan de buitenkant van de basiscirkel en de drukhoek op de basiscirkel is nul.
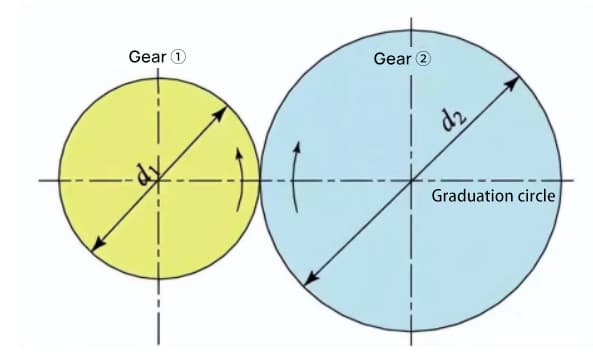
Als twee standaard evolvente tandwielen in elkaar grijpen, raken hun steekcirkels elkaar op de standaard hartafstand. Het in elkaar grijpen van de twee tandwielen lijkt op de overbrenging van twee wrijvingswielen met een diameter van respectievelijk d1 en d2.
Het in elkaar grijpen van omgekrulde tandwielen hangt echter af van de basiscirkel en niet van de steekcirkel.
De contactpunten tussen de tanden van twee tandwielen bewegen langs de actielijn in de volgorde P1, P2 en P3.
Let op de gele tand in het aandrijftandwiel. Nadat deze tand begint te mazen, bevindt het tandwiel zich een tijdje in een toestand van mazen met twee tanden (P1, P3). Het in elkaar grijpen gaat door en als het contactpunt naar punt P2 op de steekcirkel beweegt, is er nog maar één tand in de maas.
Het mazen gaat door en als het contactpunt naar punt P3 beweegt, begint de volgende tand te mazen op punt P1, waardoor er weer een maastoestand met twee tanden ontstaat. Op deze manier grijpen de tandwielen met twee tanden en de tandwielen met één tand in elkaar en brengen ze herhaaldelijk rotatiebewegingen over.
De gemeenschappelijke raaklijn tussen de basiscirkels, A-B, wordt de actielijn genoemd. De contactpunten van de tandwielparen liggen allemaal op deze actielijn.
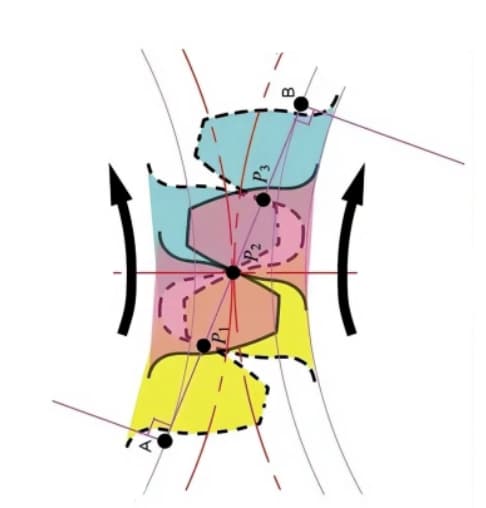
Ter illustratie: het is als een riem die over de buitenste omtrek van twee basiscirkels loopt en kracht overbrengt door roterende beweging.
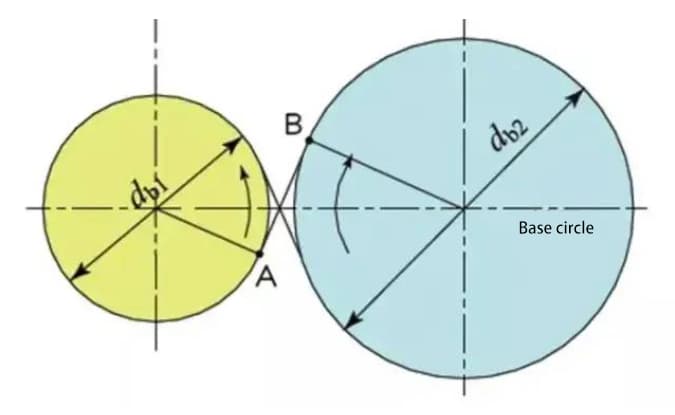
Het tandprofiel van de tandwielen die we meestal gebruiken is meestal een standaard involuut, maar er zijn ook situaties waarin de tandwieltanden verplaatst moeten worden, bijvoorbeeld om de hartafstand aan te passen of om undercutting van het kleinere tandwiel te voorkomen.
De omgekrulde tandvormcurve varieert met het aantal tanden. Hoe meer tanden, hoe meer de tandvormcurve neigt naar een rechte lijn.
Naarmate het aantal tanden toeneemt, wordt de tandwortel dikker en neemt de sterkte van het tandwiel toe.
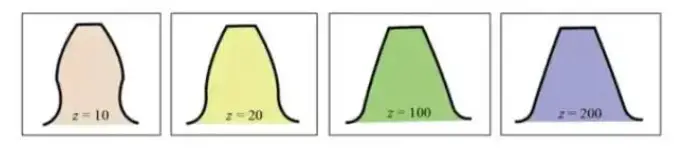
Uit de bovenstaande grafiek blijkt dat voor een tandwiel met 10 tanden een deel van het omgekrulde tandprofiel bij de tandwortel wordt verwijderd, wat resulteert in ondersnijding.
Door echter een positieve verplaatsing aan te nemen voor het tandwiel met z=10, de diameter van de addendumcirkel te vergroten en de tanddikte van de tandwieltanden te vergroten, kan dezelfde tandwielsterkte worden bereikt als die van een tandwiel met 200 tanden.
Het volgende diagram toont het schematische diagram van een 10-tands tandwiel met positieve verplaatsing. Tijdens het snijden van een tandwiel wordt de verplaatsing van het gereedschap langs de radiale richting de radiale verplaatsingshoeveelheid genoemd (ook wel verplaatsingshoeveelheid genoemd) xm(mm).
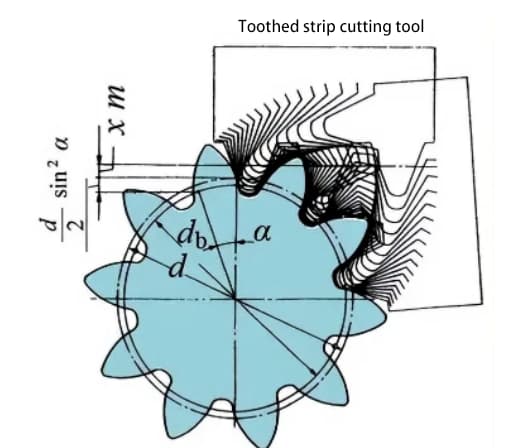
Door de positieve verplaatsing van het tandprofiel neemt de tanddikte van het tandwiel toe en neemt de buitendiameter (diameter van de toevoegingscirkel) ook toe.
Door positieve verplaatsing toe te passen, kan ondersnijden van tandwielen worden voorkomen. Verplaatsing van tandwielen kan ook andere doelen bereiken, zoals het veranderen van de hartafstand. Positieve verplaatsing kan de hartafstand vergroten, terwijl negatieve verplaatsing deze kan verkleinen.
Ongeacht of het een tandwiel met positieve of negatieve verplaatsing is, er zijn beperkingen aan de hoeveelheid verplaatsing.
De verplaatsing kan positief of negatief zijn. Hoewel de tandhoogte hetzelfde is, verschilt de tanddikte. Een tandwiel met een verdikte tanddikte is een positief verplaatsend tandwiel, terwijl een tandwiel met een gereduceerde tanddikte een negatief verplaatsend tandwiel is.
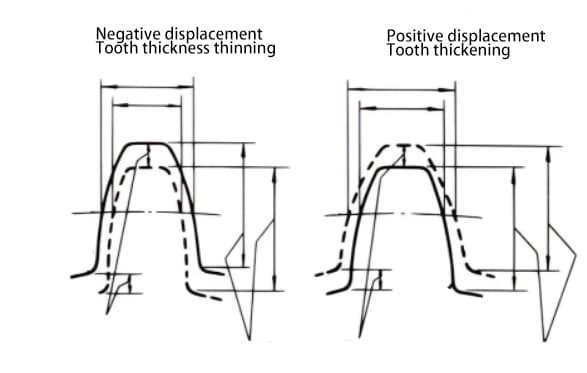
Als het niet mogelijk is om de hartafstand tussen twee tandwielen te wijzigen, kan een positieve verplaatsing worden toegepast op het kleinere tandwiel (om ondersnijden te voorkomen) en een negatieve verplaatsing op het grotere tandwiel om dezelfde hartafstand te verkrijgen. In dit geval is de absolute waarde van de verplaatsingshoeveelheid gelijk.
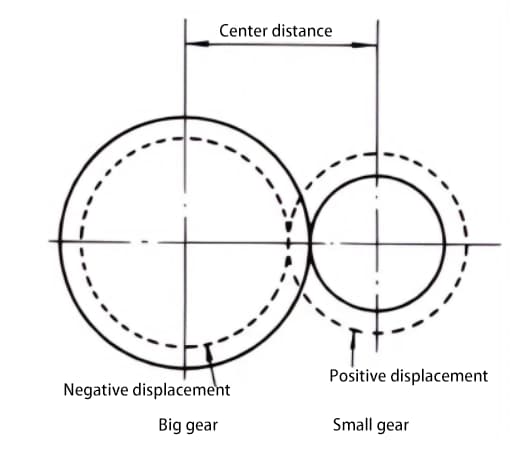
Standaard tandwielen grijpen in elkaar als hun steekcirkels elkaar raken. Verplaatste tandwielen, zoals te zien is in de figuur, raken elkaar op de steekcirkel.
De drukhoek op de maascirkel wordt de maashoek genoemd. De maashoek verschilt van de drukhoek op de steekcirkel (steekcirkeldrukhoek) en is een belangrijke factor in het ontwerp van verplaatste tandwielen.
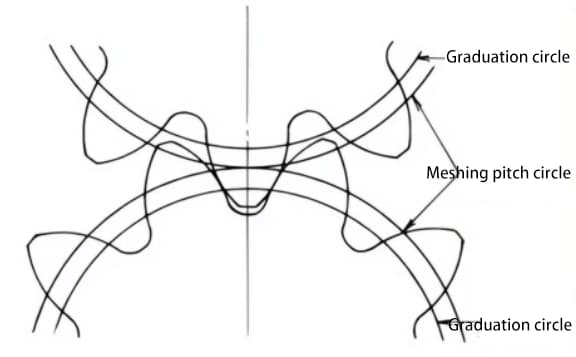
Tandwielverplaatsing kan ondersnijding voorkomen die wordt veroorzaakt door een klein aantal tanden tijdens het bewerken. De gewenste hartafstand kan worden verkregen door middel van verplaatsing.
Bij een tandwielpaar met een groot verschil in aantal tanden kan positieve verplaatsing worden toegepast op het gemakkelijk versleten kleinere tandwiel om de tanddikte te vergroten, terwijl negatieve verplaatsing kan worden toegepast op het grotere tandwiel om de tanddikte te verkleinen, zodat de levensduur van de twee tandwielen beter vergelijkbaar wordt.
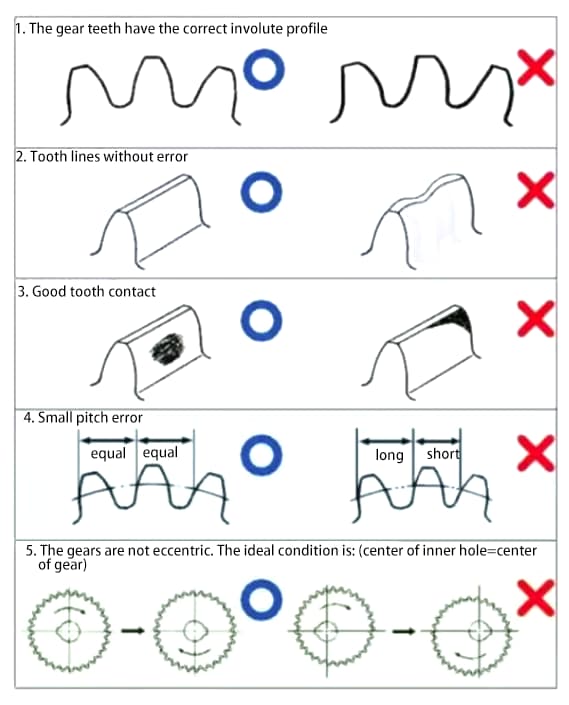
Tandwielen zijn mechanische onderdelen die kracht en rotatie overbrengen. De belangrijkste vereisten voor tandwielprestaties zijn:
Om aan de bovenstaande eisen te voldoen, wordt het verbeteren van de tandwielnauwkeurigheid een noodzakelijke taak.
De nauwkeurigheid van tandwielen kan grofweg worden onderverdeeld in drie categorieën:
a) Nauwkeurigheid van het omgekrulde tandprofiel - nauwkeurigheid van het tandprofiel
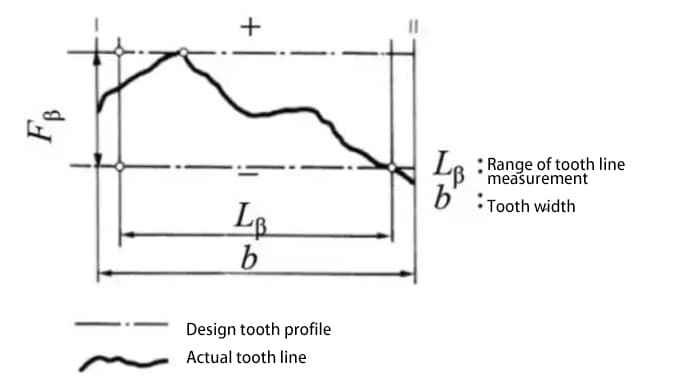
b) Nauwkeurigheid van de tandflanklijn op het tandoppervlak - nauwkeurigheid van de tandlijn
c) Nauwkeurigheid van tand/gleuf positie.
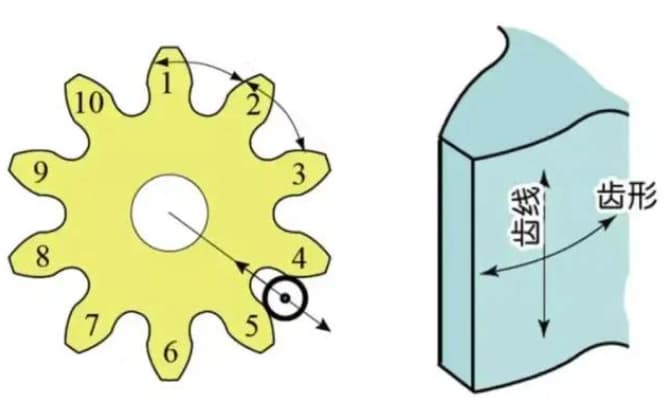
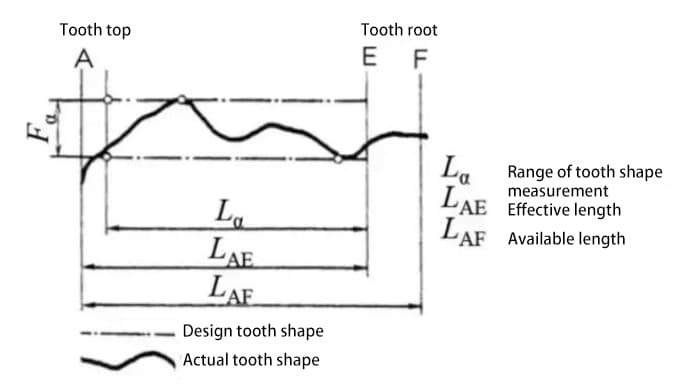
De tandprofielfout is de fout tussen het werkelijke tandprofiel van het tandwiel en het theoretische tandprofiel.
Er zijn veel factoren die de fout in het tandprofiel beïnvloeden, zoals het gereedschap en de trillingen van de machine tijdens het zagen.
De tandprofielfout beïnvloedt de tandwieloverbrengingsprestaties en het geluid. Daarom is het noodzakelijk om de tandprofielfout binnen het toegestane bereik te houden.
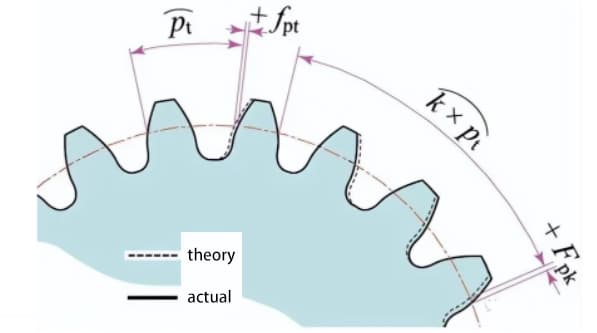
Meet de steekwaarde op de meetomtrek gecentreerd op de tandwielas.
Een afwijking in tandsteek (fpt) is het verschil tussen de werkelijke tandsteek en de theoretische tandsteek.
De totale cumulatieve toonhoogteafwijking (Fp) wordt gebruikt om de afwijking van de hele tandwielsteek te evalueren. De totale amplitudewaarde van de curve van de cumulatieve steekafwijking vertegenwoordigt de totale steekafwijking.
Plaats achtereenvolgens een sonde (bolvormig of cilindrisch) in de tandgroef en meet het verschil tussen de maximale en minimale radiale afstanden van de sonde tot de tandwielas. Excentriciteit van de tandwielas is een van de factoren die bijdraagt aan radiale uitloop.
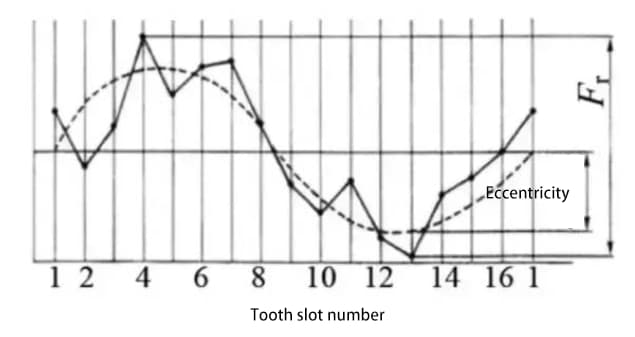
Tot nu toe zijn de methoden die we hebben beschreven voor het evalueren van de nauwkeurigheid van tandwielen, zoals tandvorm, spoed en tandflanknauwkeurigheid, allemaal methoden voor het evalueren van de nauwkeurigheid van een individueel tandwiel.
Er is daarentegen een andere methode waarbij de tandwielnauwkeurigheid wordt beoordeeld door een tandwiel met twee tanden te testen in combinatie met een meettandwiel. De twee oppervlakken van het geteste tandwiel grijpen in elkaar met het meettandwiel en draaien gedurende een hele cyclus. De verandering in hartafstand wordt geregistreerd.
De onderstaande figuur toont de testresultaten voor een tandwiel met 30 tanden. Er zijn in totaal 30 golflijnen voor de radiale composietafwijking van één tand.
De radiale composietafwijkingswaarde is ongeveer de som van de radiale uitloopafwijking en de radiale composietafwijking van één tand.
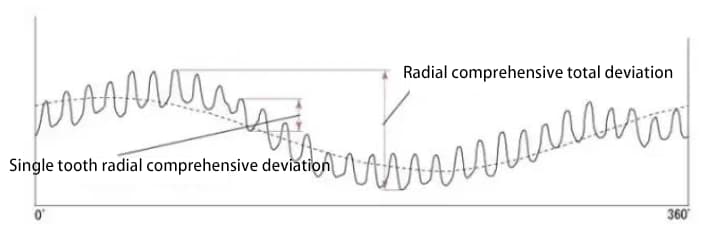
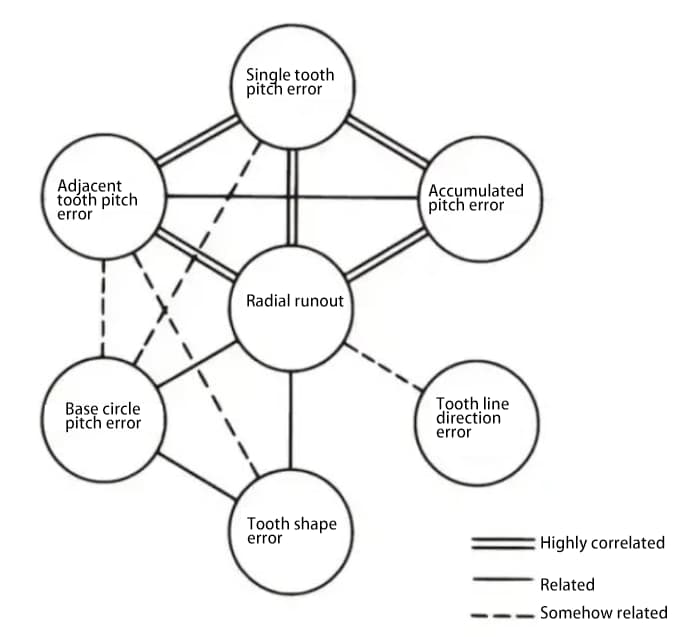
De verschillende onderdelen van de tandwielnauwkeurigheid zijn aan elkaar gerelateerd. In het algemeen is de radiale uitloop sterk gecorreleerd met andere fouten en is er ook een sterke correlatie tussen verschillende steekfouten.
Spiraalhoek op een normale cilindrische doorsnede:
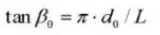
Spiraalhoek op een basiscilinder:
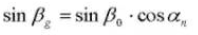
Tanddikte centreerhoek:
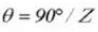
Diameter pen:
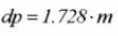
Correctiefactor voor middenafstand:
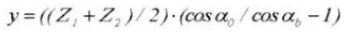
Berekening van standaard rechte tandwielen (rondsel ①, tandwiel ②)
1. Aantal tanden op tandwielstandaard
2. Standaard rechte tandwielen met voluut tandwielprofiel
3. Module m
4. Drukhoek
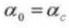
5. Aantal tanden
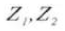
6. Effectieve tanddiepte
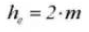
7. Gehele tanddiepte
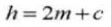
8. Vrijloop tandwielen
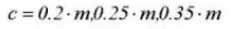
9. Referentie steekcirkeldiameter
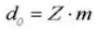
10. Buitendiameter
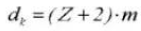
11. Worteldiameter
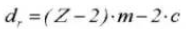
12. Diameter basiscirkel
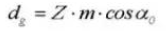
13. Cirkelvormige steek
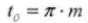
14. Normale verticale hoek
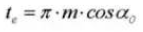
15. Dikte ronde tanden
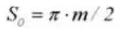
16. Chordale tanddikte
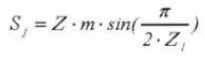
17. Hoogte peilstok tanden
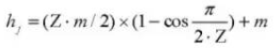
18. Aantal tanden tegenover elkaar
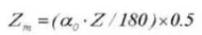
19. Tanddikte overdwars
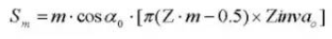
20. Diameter pen
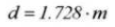
21. Cilindrische meetafmeting
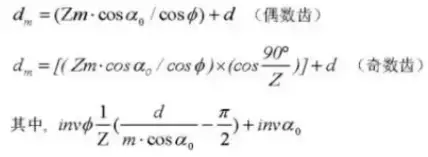
Formule voor het berekenen van verschoven tandwielen (rondsel ①, tandwiel ②):
1. Tandwielprofiel Dwars
2. Contactverhouding gereedschapstandprofiel
3. Module m
4. Drukhoek
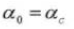
5. Aantal tanden Z
6. Effectieve tanddiepte
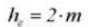
7. Gehele tanddiepte
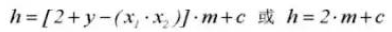
8. Speling tandwiel C
9. Verhouding dwarscontact X
10. Afstand tot het midden
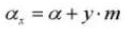
11. Referentie steekcirkeldiameter
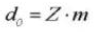
12. Werkdrukhoek
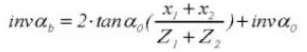
13. Diameter steekcirkel
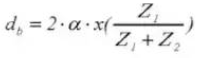
14. Buitendiameter
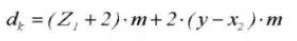
15. Addendum Diameter
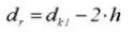
16. Diameter steek
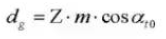
17. Cirkelvormige steek
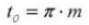
18. Normale verticale hoek
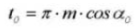
19. Dikte ronde tanden
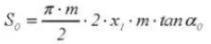
20. Chordale tanddikte
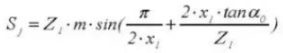
21. Tandwielmeter Tandhoogte
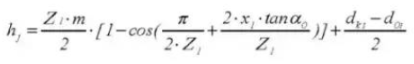
22. Aantal tanden tegenover elkaar
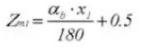
23. Tanddikte tegenover
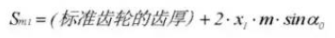
24. Diameter uiteinde
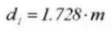
25. Dwarsmaat

Formule voor het berekenen van standaard rechte tandwielen (normaal systeem) (rondsel ①, tandwiel ②)
1. Tandwielprofiel standaard
2. Referentiegedeelte van tandprofiel normaal systeem
3. Gereedschap Tandprofiel Rechte Tandwielen
4. Module
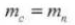
5. Drukhoek
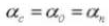
6. Aantal tanden
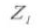
7. Helix Richting
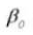
8. Effectieve tanddiepte
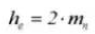
9. Gehele tanddiepte
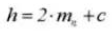
10. Drukhoek voorkant
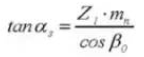
11. Afstand tot het midden
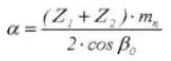
12. Referentie steekcirkeldiameter
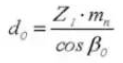
13. Buitendiameter
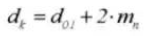
14. Worteldiameter
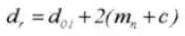
15. Diameter steek
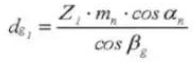
16. Helixhoek op basiscirkel
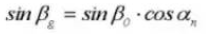
17. Standplaats
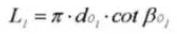
18. Cirkelvormige verticale hoek (normaal systeem)
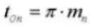
19. Normale verticale hoek (normaal systeem)
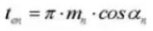
20. Ronde tanddikte (normaal systeem)
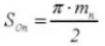
21. Equivalent aantal tanden op een standaard tandwiel
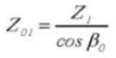
22. Chordale tanddikte
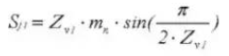
23. Tandwielkijkmaat Tanddiepte
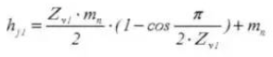
24. Aantal tanden tegenover elkaar
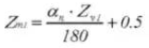
25. Tanddikte overdwars
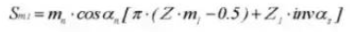
26. Diameter uiteinde
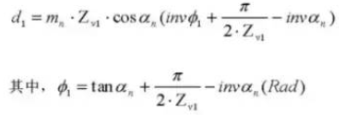
27. Cilindrische meetafmeting

28. Speling tandwiel f
Formule voor het berekenen van de verplaatsing van schuine tandwielen (normaal systeem) (rondsel ①, tandwiel ②):
1. Tandwielprofiel verplaatst
2. Referentiegedeelte van tandprofiel normaal systeem
3. Gereedschap tandprofiel rechte tandwielen
4. Module (normaal systeem)
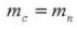
5. Drukhoek (normaal systeem)
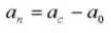
6. Aantal tanden
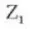
7. Helix Richting
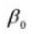
8. Effectieve tanddiepte
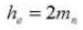
9. Gehele tanddiepte
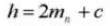
10. Verhouding dwarscontact
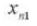
11. Afstand tot het midden
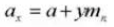
12. Normale module
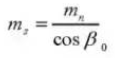
13. Drukhoek voorkant (normaal systeem)
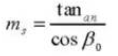
14. Equivalent aantal tanden op een standaard tandwiel
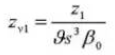
15. Normale drukhoek systeem
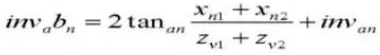
16. Referentie steekcirkeldiameter
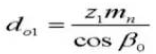
17. Buitendiameter
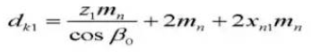
18. Diameter steek van contacttanden
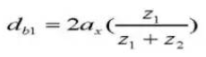
19. Diameter steek
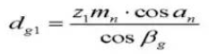
20. Spiraalhoek op basiscilinder
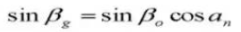
21. Dikte ronde tanden
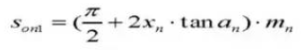
22. Chordale tanddikte
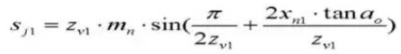
23. Tandwielmeter Tandhoogte.
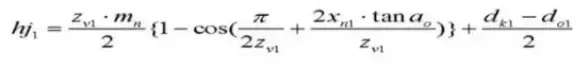
24. Aantal tanden tegenover elkaar
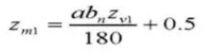
25. Tanddikte overdwars

26. Diameter pen.
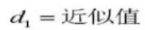
27. Cilindrische meetafmeting