Heb je je ooit afgevraagd hoe precisie en efficiëntie samenkomen bij industrieel knippen? Dit artikel verkent de fascinerende wereld van guillotinescharen en beschrijft hun voordelen en uitdagingen. Leer hoe mechanische analyse en optimalisatie de prestaties kunnen verbeteren, zodat u voorop blijft lopen op het gebied van werktuigbouwkunde.
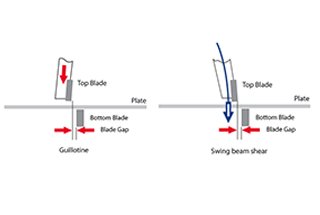
De guillotineschaar is efficiënter, preciezer en betrouwbaarder dan de zwenkbalkschaar, omdat er geen speling in de structuur is en de kniphoek kan worden aangepast.
Bij het knippen van brede, zware platen of dunne platen met een hoge sterkte kan de guillotineschaar echter te maken krijgen met uitdagingen zoals vervorming van de machine die de knipnauwkeurigheid beïnvloeden.
Het meeste onderzoek op dit gebied richt zich op de invloed van afschuifparameters op de nauwkeurigheid, het ontwerp en de automatisering van het besturingssysteem of het simuleren van het afschuifproces met behulp van discrete punten.
Er is echter beperkt onderzoek gedaan naar de analyse van mechanische eigenschappen en de optimalisatie van de structuur van guillotinescharen.
Dit artikel wil deze leemte opvullen door de statische en dynamische karakteristieken van de bewerkingsmachine te analyseren en het plaatschuifproces te simuleren. Door deze analyse worden continue afschuifgegevens verkregen en wordt een optimalisatieschema voorgesteld.
Een constructiemodel van een 6 x 3200 NC guillotineschaar wordt getoond in Figuur 1. Tijdens het gebruik past de terugloopblokkering, aangedreven door de rollerscrew, de snijlengte aan. De perscilinder wordt vervolgens samengedrukt door de snijplaat.
Zodra de snijparameters, zoals messpeling en kniphoek, zijn ingesteld, drijven de hydraulische cilinders aan beide uiteinden de bovenste en onderste messen aan om te bewegen en de snede te voltooien. plaat snijden proces.
In de simulatieanalyse worden de overgangsvulling en het draadgat buiten beschouwing gelaten en wordt een vereenvoudigd driedimensionaal model geïmporteerd in een eindige-elementenanalysesoftware. De twee zijden van de bovenste gereedschapshouder worden vastgezet met constraints en er wordt bindingscontact gemaakt om het lassen en de schroefdraadbevestiging van de bovenste gereedschapshouderdelen te simuleren.
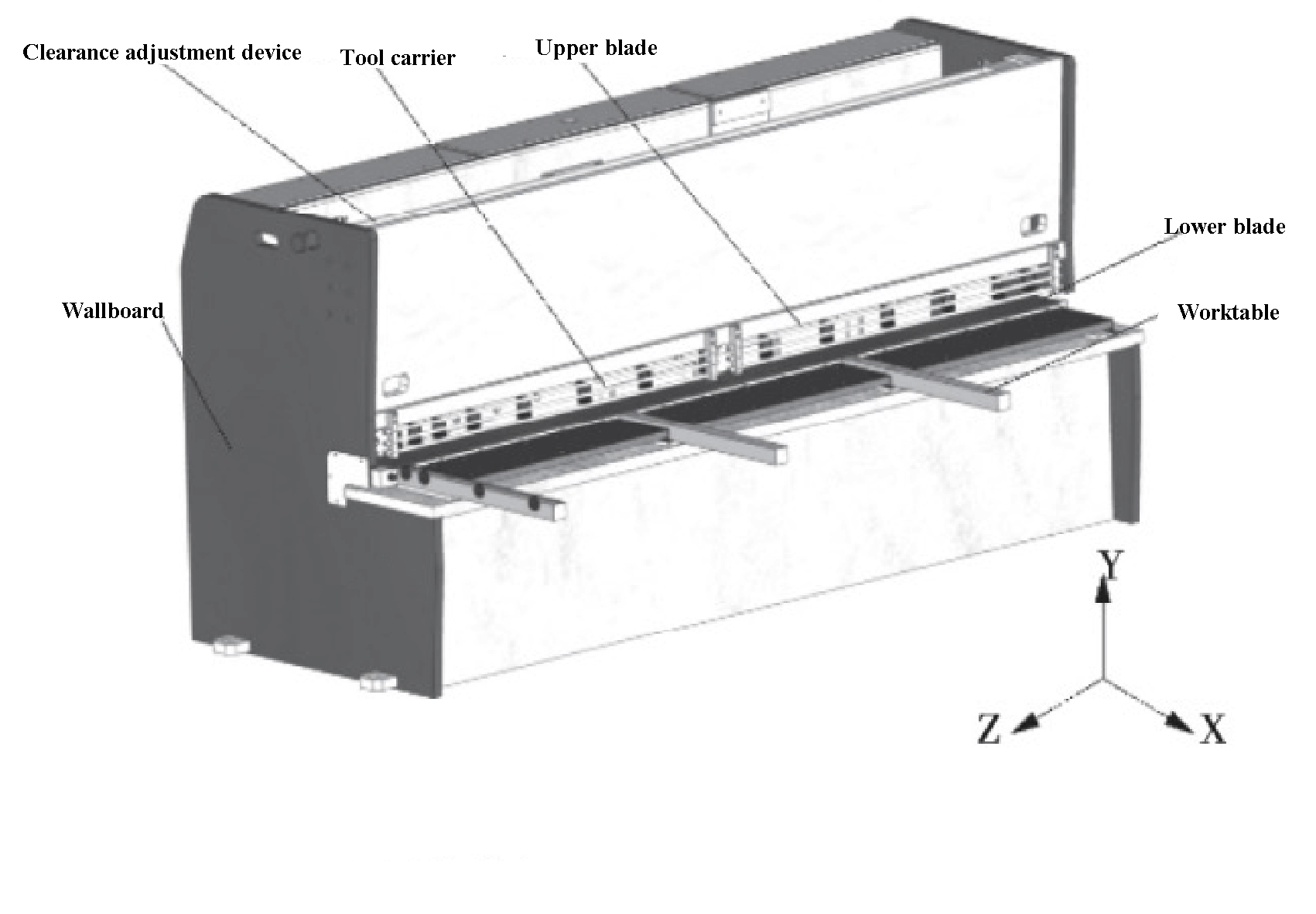
Fig. 1 Constructiemodel van 6 × 3200 NC guillotineschaar
Volgens de formule van Norsali:

In de formule:
De verticale dwarskracht (P1) wordt berekend op 212,8 kN met formule (1), terwijl de horizontale dwarskracht (P2) wordt geschat op 30% van de verticale dwarskracht, of 63,8 kN. Zowel de verticale als de horizontale dwarskrachten worden toegepast op de bovenste koepel en opgelost met ANSYS Workbench.
De vervorming in elke richting aan het begin, in het midden en aan het einde van het afschuiven wordt vergeleken en geanalyseerd. Zoals te zien is in tabel 1, is de vervorming van de bovenste slede in de Y-richting het grootst en kan de vervorming in de X- en Z-richting in vergelijking als verwaarloosbaar worden beschouwd.
De begin- en eindpositie van de vervorming in Y-richting zijn ongeveer gelijk en veel minder dan de middenpositie. Tijdens het afschuifproces vertoont de vervorming van de bovenste gereedschapshouder een holle trend.
Tabel 1 Maximale equivalente spanning en maximale vervorming in X-, Y- en Z-richting van de bovenste gereedschapshouder
| Schuifstand | Maximale equivalente spanning /MPa | Maximale vervorming in X-richting /mm | Maximale vervorming in Y-richting /mm | Maximale vervorming in Z-richting /mm |
| Begin | 137.7 | 0.020 | 0.141 | 0.074 |
| Midden | 135.3 | 0.090 | 0.183 | 0.650 |
| Einde | 137.2 | 0.013 | 0.151 | 0.085 |
Figuren 2 en 3 tonen respectievelijk de maximale equivalente spanning in het midden en de maximale vervorming in de Y-richting.

Fig. 2 Maximale equivalente spanning van de bovenste gereedschapshouder
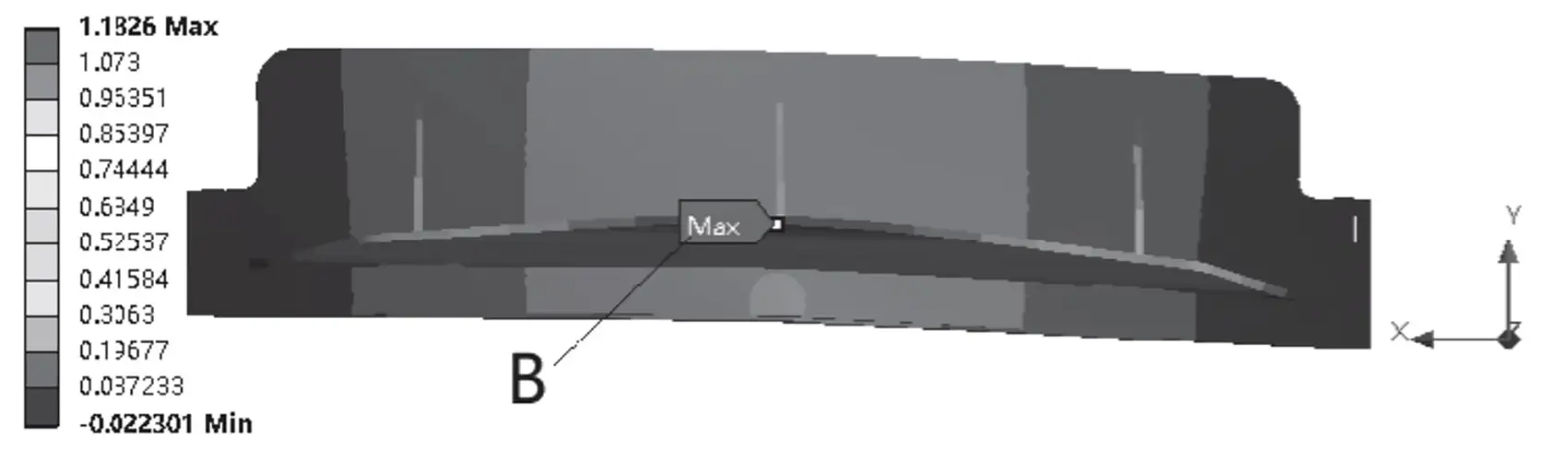
Fig. 3 Maximale vervorming van de bovenste gereedschapshouder in Y-richting
Door tabel 1 en figuren 2 en 3 te analyseren, kan worden vastgesteld dat de equivalente spanning van de bovenste gereedschapshouder het hoogst is aan het begin van het afschuifproces. Deze spanning bevindt zich op de positie van de hydraulische cilinder en heeft een waarde van 137,7 MPa, wat lager is dan de treksterkte van 235 MPa voor de bovenste gereedschapsteun.
In het midden van het afschuifproces wordt de maximale vervorming van de bovenste gereedschapshouder in de Y-richting waargenomen bij de achterste steunplaat B, met een grootte van 1,183 mm. Ondertussen is de vervorming van het blad in de Y-richting 0,346 mm, wat minder is dan 1 mm en voldoet aan de noodzakelijke vereisten.
In de dynamische simulatie wordt een schuif op de beginpositie van het bovenste blad geplaatst en constant onderworpen aan de schuifkracht met een bepaalde snelheid. De beweging van de schuif wordt gebruikt om het afschuifproces van de plaat te simuleren.
Aangezien de glijder alleen schuifkracht overbrengt, is deze ingesteld op wrijvingsloos contact met het bovenmes. Tijdens het snijden van de plaatmetaalHet contact tussen het bovenste blad en het te snijden plaatmetaal wordt geïllustreerd in Figuur 4. De contactlengte (s) is 8:1.

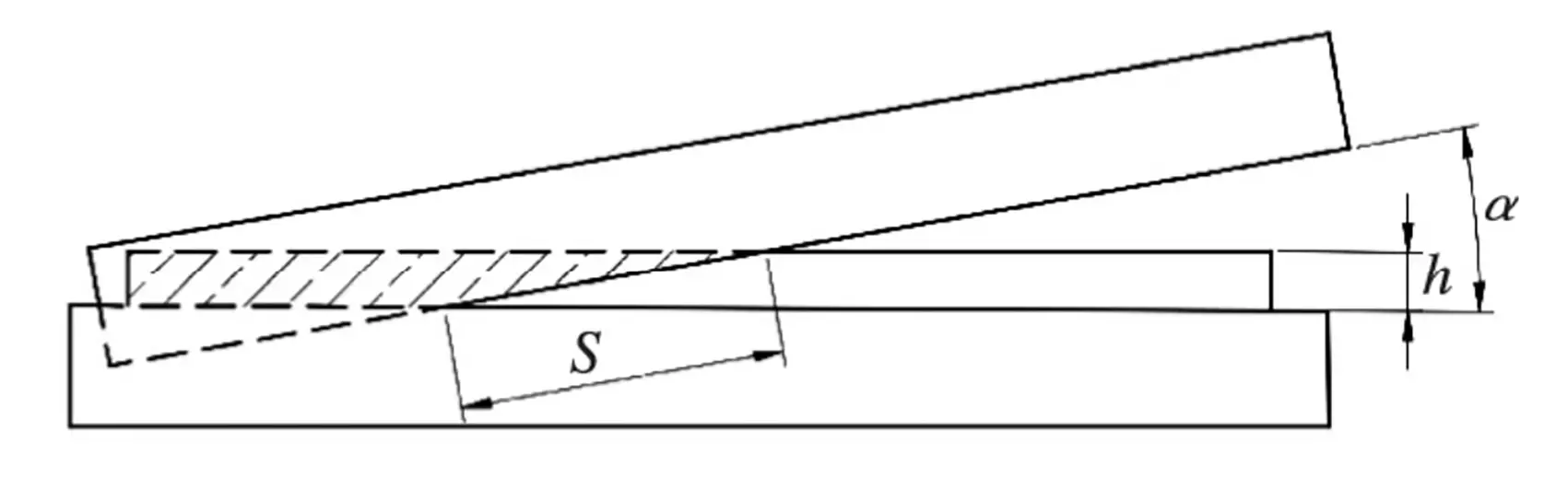
Fig. 4 Snijddiagram
Om de berekening te vereenvoudigen wordt aangenomen dat de dwarskracht gelijkmatig verdeeld is over een rechthoekig gebied met de lengte (s) en breedte (t) van de schoep. Bijgevolg wordt de glijschijf gemodelleerd als een kubus met dezelfde lengte (s) en breedte (t), zoals weergegeven in figuur 5.

Fig. 5 Schematisch diagram van schuifsimulatie
Door de maximale equivalente spanning en maximale vervorming in de Y- en Z-richting bij elke positie op te lossen, worden de resultaten weergegeven in tabel 2. De trend van de vervorming en spanning van de bovenste gereedschapshouder tijdens het afschuifproces wordt getoond in figuur 6.
Tabel 2 maximale equivalente spanning en maximale vervorming in Y- en Z-richting van de bovenste gereedschapshouder bij elke belastingsstap
| Stap laden | Maximale equivalente spanning /MPa | Maximale vervorming in Y-richting /mm | Maximale vervorming in Z-richting /mm |
| 1 | 138.1 | 0.265 | 0.181 |
| 2 | 153.2 | 0.380 | 0.330 |
| 3 | 158.4 | 0.403 | 0.386 |
| 4 | 159.2 | 0.469 | 0.426 |
| 5 | 157.5 | 0.592 | 0.463 |
| 6 | 153.8 | 0.571 | 0.454 |
| 7 | 148.1 | 0.580 | 0.461 |
| 8 | 150.3 | 0.635 | 0.478 |
| 9 | 153.7 | 0.543 | 0.458 |
| 10 | 154.9 | 0.477 | 0.446 |
| 11 | 153.2 | 0.482 | 0.425 |
| 12 | 141.8 | 0.358 | 0.336 |
| 13 | 136.4 | 0.250 | 0.175 |
Zoals te zien is in Tabel 2 en Figuur 6, verandert de vervorming van de bovenste gereedschapshouder met de verandering in de afschuifpositie. De vervorming is aanzienlijk in het midden en relatief klein en symmetrisch aan beide zijden, wat overeenkomt met de resultaten van de statische simulatie.
De maximale vervorming van de bovenste gereedschapshouder in de Y- en Z-richting treedt op in belastingsstap 8, met waarden van respectievelijk 0,635 mm en 0,478 mm, dus minder dan 1 mm.
De maximale equivalente spanning wordt gevonden in belastingsstap 4 en heeft een waarde van 159,2 MPa, wat lager is dan de vloeigrens van 235 MPa voor de bovenste gereedschapshouder.
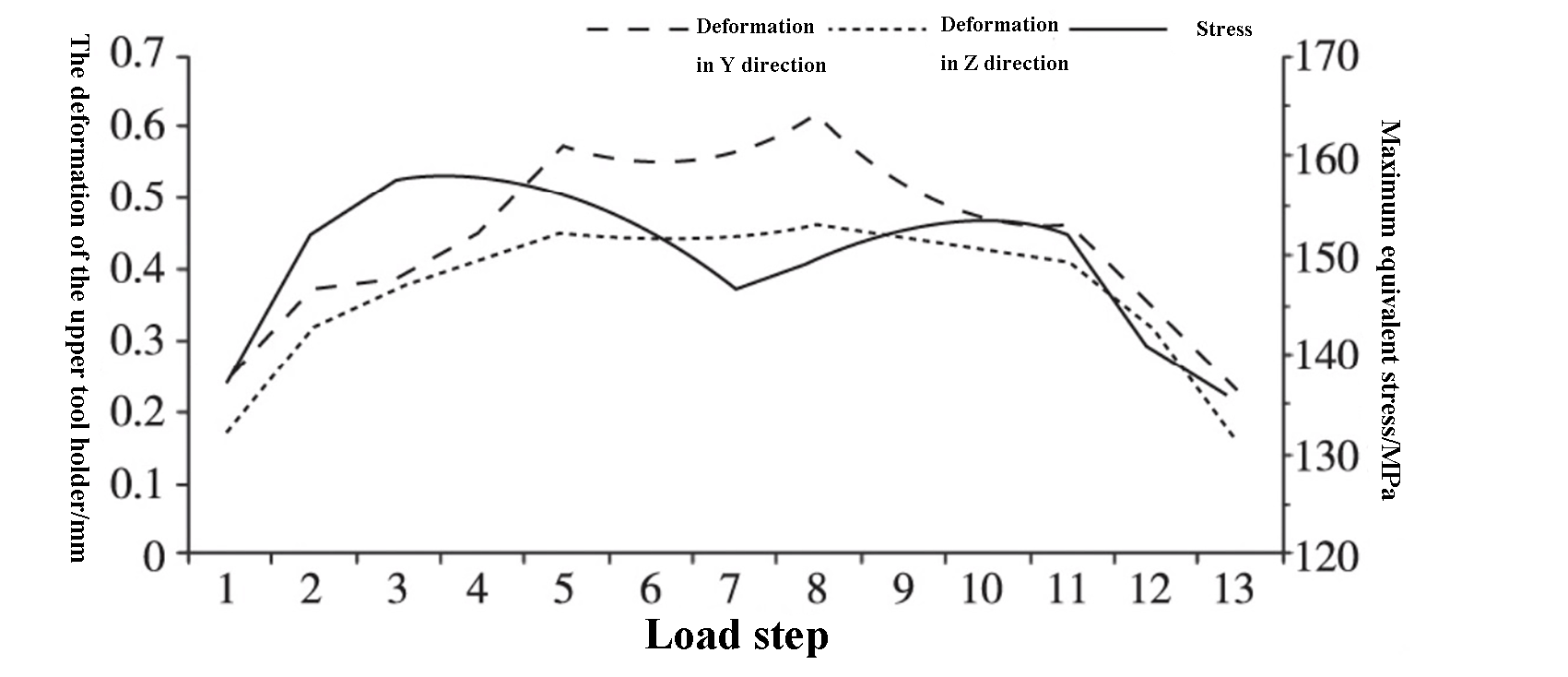
Fig. 6 Vervorming en maximale equivalente spanning van de bovenste gereedschapshouder in Y- en Z-richting
Figuren 7, 8 en 9 tonen de maximale vervorming en maximale equivalente spanning in respectievelijk de Y- en Z-richting.

Fig. 7 Maximale vervorming van de bovenste gereedschapshouder in Y-richting

Fig. 8 Maximale vervorming van de bovenste gereedschapshouder in Z-richting

Fig. 9 Maximale equivalente spanning van de bovenste gereedschapshouder
Uit de figuren 7, 8 en 9 blijkt dat de maximale vervorming van de bovenste slede in de Y-richting optreedt bij blad C, terwijl de maximale vervorming in de Z-richting optreedt bij blad D. Beide vervormingen zijn minder dan 1 mm en voldoen aan de ontwerpvereisten.
De maximale equivalente spanning treedt op bij positie E van de bovenste gereedschapshouder onder invloed van de hydraulische cilinder. De spanning op het blad is minimaal en vertoont een goede stijfheid.
In de modale analyse worden de vier bases van het frame gefixeerd en op hun plaats gehouden met constraints. De Block Lanczos methode wordt gekozen als de modusextractiemethode en het aantal uitgebreide modi wordt ingesteld op 4 om de eerste vier natuurlijke frequenties van de frameconstructie op te lossen.
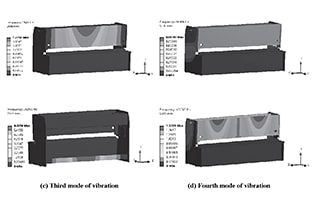
De vier trillingsmodes worden getoond in Figuur 10 en Tabel 3 toont de eigenfrequenties, amplitudes en modale vormen van de vier structurele trillingsmodes.
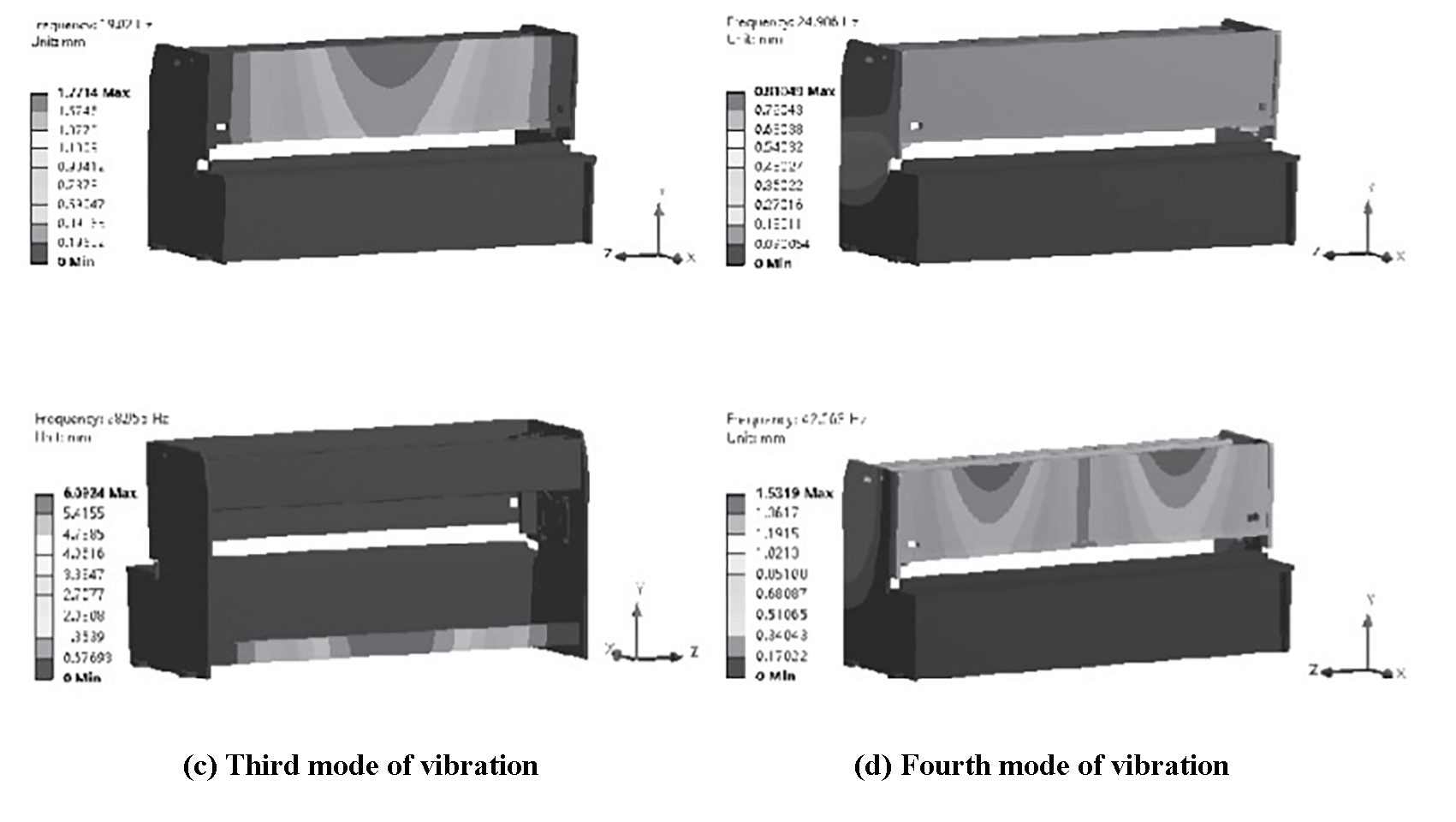
Fig. 10 De vier trillingsmodes
Tabel 3 Modale analyse gegevenstabel van plaatschuiven
| Bestel | Frequentie /Hz | Amplitudes /mm | Trilmodus |
| 1 | 19.02 | 1.77 | Het voorpaneel is naar voren gebogen in de X-richting |
| 2 | 24.98 | 0.81 | Het bovenste deel van het frame buigt en zwaait in Z-richting |
| 3 | 28.96 | 6.09 | De onderste draagbalk wordt in de X-richting naar voren gebogen |
| 4 | 42.66 | 1.53 | Het voorpaneel is heen en weer gebogen in X-richting |
Op basis van Figuur 10 en Tabel 3 is te zien dat de trillingsvervorming van het frame voornamelijk invloed heeft op het voorpaneel en de onderste steunbalk, wat aanzienlijke trillingen en geluid veroorzaakt. Bij een frequentie van 19,02 Hz is de amplitude van het voorpaneel hoger, wat het afschuifproces negatief kan beïnvloeden en de nauwkeurigheid kan verminderen.
De knipfrequentie van de NC guillotineschaar is echter 9 keer per minuut, wat aanzienlijk lager is dan de natuurlijke frequentie van de eerste orde en voldoet aan de eisen voor normaal gebruik.
Het is belangrijk om de invloed van externe trillingsbronnen tijdens het werkproces te minimaliseren om overmatige vervorming door trillingen te voorkomen.
De analyse van de statische en dynamische karakteristieken van het afschuifproces toont aan dat de vervorming van de bovenste revolver een concave trend vertoont tijdens het afschuiven, wat de braam- en maatnauwkeurigheid van de blanking kan beïnvloeden en de algehele afschuifkwaliteit kan verminderen.
Om de snijkwaliteit te verbeteren, kan de bladspeling in de snijparameters worden aangepast om de positioneringsstijfheid van de bovenste gereedschapshouder te vergroten. In dit artikel is een dynamische schuine geleider voor het instellen van de snijkantafstand ontworpen, zoals weergegeven in figuur 11.

Fig. 11 Structuurschema van de schuine geleiderail guillotineschaar