Heb je je ooit afgevraagd hoe plaatontwerpers de nauwkeurigheid van hun ontwerpen garanderen? In deze blogpost duiken we in de fascinerende wereld van plaatontwerp en verkennen we twee essentiële concepten: buigtoeslag en buigaftrek. We introduceren ook de K-factor en zijn rol in berekeningen. Volg ons terwijl we deze onderwerpen ontrafelen en waardevolle inzichten geven van experts uit de industrie.
Op het gebied van plaatontwerp zijn begrippen als buigtoeslag, buigaftrek en K-factor cruciale concepten die de nauwkeurigheid en efficiëntie van productieprocessen aanzienlijk beïnvloeden. Deze parameters spelen een essentiële rol bij het bepalen van de uiteindelijke afmetingen van gebogen plaatwerkonderdelen en zorgen voor een nauwkeurige fabricage. Laten we eens dieper ingaan op deze concepten en hun berekeningsmethoden onderzoeken.
Ingenieurs en fabrikanten die betrokken zijn bij de fabricage van plaatwerk gebruiken geavanceerde algoritmes om de vlakke patroonafmetingen van onderdelen nauwkeurig te berekenen, zodat de uiteindelijke geometrieën na het buigen en vormen nauwkeurig zijn.
De traditionele "knijpmethode" blijft een veelgebruikte empirische benadering die rekening houdt met factoren zoals materiaaleigenschappen, buigradius, buighoek, gereedschapconfiguraties en vormsnelheden. Deze methode is weliswaar effectief, maar is sterk afhankelijk van de ervaring van de operator en kan inconsistent zijn.
Met de komst van geavanceerde rekenhulpmiddelen hebben computerondersteund ontwerp (CAD) en eindige-elementenanalyse (FEA) een revolutie teweeggebracht in de nauwkeurigheid en efficiëntie van plaatontwerp. Deze technologieën maken een nauwkeurige simulatie mogelijk van het materiaalgedrag tijdens het vervormingsproces, waarbij rekening wordt gehouden met complexe fenomenen zoals terugvering, restspanningen en rekverharding.
Moderne CAD-systemen maken gebruik van geavanceerde algoritmen voor buigcompensatie die theoretische modellen integreren met empirische gegevens. Deze algoritmen gebruiken meestal een van de twee primaire benaderingen:
Toonaangevende CAD-platforms, zoals SolidWorks, Autodesk Inventor en Siemens NX, bieden robuuste modules voor het ontwerpen van plaatwerk met aanpasbare buigtafels en materiaalbibliotheken. Deze systemen maken de integratie van werkplaatsspecifieke buiggegevens mogelijk, zodat de digitale ontwerpen en de daadwerkelijke productieprocessen op elkaar zijn afgestemd.
Bovendien worden opkomende technologieën zoals machine learning en kunstmatige intelligentie toegepast om buigberekeningen te optimaliseren, waarbij enorme datasets van historische productiegegevens worden gebruikt om voorspellingen te verfijnen en aan te passen aan unieke combinaties van materialen en gereedschappen.
Om de lezer meer inzicht te geven in de basisconcepten in ontwerp plaatmetaal berekening worden de volgende punten samengevat en uitgelegd:
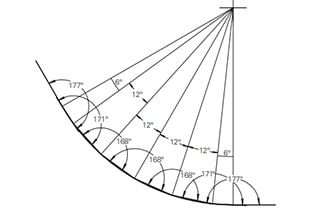
Voor een beter begrip van BuigtoelageZie afbeelding 1, die een enkele buiging in een plaatmetalen onderdeel illustreert. Figuur 2 toont het onderdeel in uitgeklapte toestand.
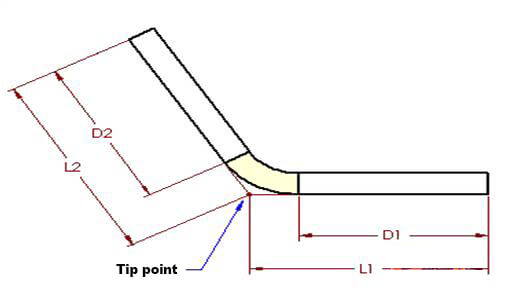
Figuur 1
Figuur 2
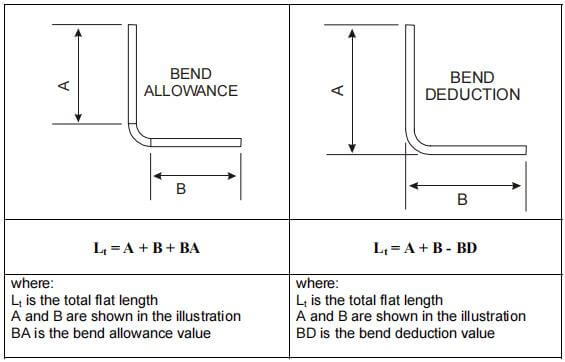
Het buigtoeslagalgoritme beschrijft de ongevouwen lengte (LT) van een plaatmetalen onderdeel als de som van de lengtes van elk segment nadat het onderdeel is afgevlakt, plus de lengte van het afgevlakte buiggebied.
De Buigtoelage (BA) vertegenwoordigt de lengte van het afgeplatte buiggebied. De totale lengte van het onderdeel kan dus worden uitgedrukt als vergelijking (1):
LT = D1 + D2 + BA (1)
Het buiggebied (lichtgeel weergegeven in de afbeelding) is het gebied dat theoretisch gezien vervorming ondergaat tijdens het buigproces.
Volg deze stappen om de geometrie van het uitgevouwen werkstuk te bepalen:
De taak om de lengte van het afgeplatte buiggebied te bepalen, voorgesteld door BA in de figuur, is iets lastiger.
De waarde van BA varieert op basis van factoren zoals materiaaltype, materiaaldikte, buigradius en hoek, evenals het buigproces, het machinetype en de machinesnelheid.
De waarde van BA kan worden verkregen uit verschillende bronnen, waaronder leveranciers van plaatmateriaal, experimentele gegevens, ervaring en technische handleidingen.
In SolidWorks kan men rechtstreeks BA-waarden invoeren of de K-factor (die later wordt besproken) gebruiken om de waarden te berekenen.
De buigtafel methode is de meest nauwkeurige manier om verschillende buigtoeslagen te specificeren voor verschillende situaties met verschillende diktes, radii en hoeken.
Het maken van de eerste buigtafel kan wat tijd in beslag nemen, maar als hij eenmaal gevormd is, kunnen delen ervan in de toekomst opnieuw gebruikt worden.
Voor elke bocht in het onderdeel kan dezelfde of andere informatie worden ingevoerd.
1) Normen voor algemeen buigen
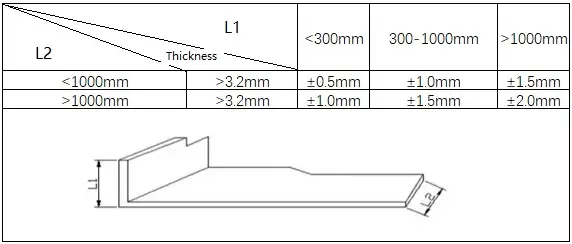
2) Normen voor Z-buigen
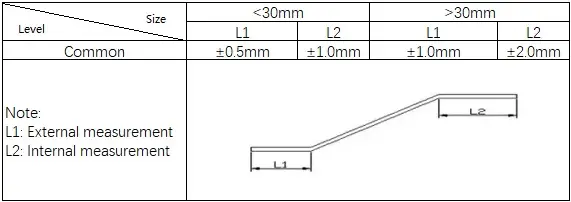
3) Normen voor V-buigen
4) Normen voor U buigen
Gerelateerde lectuur: V- & U-vormige buigkracht calculator
Buigaftrek is een term die wordt gebruikt om de hoeveelheid terugslag te beschrijven in het proces van buigen van plaatmetaal. Dit is een ander eenvoudig algoritme om het proces te beschrijven.
De figuren 1 en 2 zijn ook van toepassing op dit concept. Volgens de buigaftrekmethode is de afgeplatte lengte (LT) van het onderdeel gelijk aan de som van de lengtes van de twee vlakke delen tot aan het "punt" (het hypothetische snijpunt van de twee vlakke delen), min de buigaftrek (BD).
De totale lengte van het onderdeel kan dus worden uitgedrukt zoals in vergelijking (2):
LT = L1 + L2 - BD (2)
De waarde van BD kan worden bepaald of verkregen uit verschillende bronnen, zoals bladen metaalmateriaal leveranciers, experimentele gegevens, ervaring, technische handleidingen met vergelijkingen of tabellen, enz.
Figuur 3
Het is belangrijk dat gebruikers die bekend zijn met de buigaftrekmethode de relatie begrijpen met de buigtoelagemethode, die algemeen wordt toegepast in SolidWorks.
De relatie tussen de twee waarden kan eenvoudig worden afgeleid door gebruik te maken van de twee geometrieën van het buigen en ontvouwen van onderdelen.
Door vergelijking (1) en (2) te vergelijken, hebben we:
LT = D1 + D2 + BA (1) LT = L1 + L2 - BD (2)
En daarom,
D1 + D2 + BA = L1 + L2 - BD (3)
In Figuur 3 stelt hoek A de buighoekdie de hoek beschrijft die het onderdeel tijdens het buigen maakt en ook de hoek van de boog die wordt gevormd door het buiggebied, dat in twee helften wordt weergegeven.
Door de afmetingen en principes van rechthoekige driehoeken te gebruiken, kunnen we de volgende vergelijkingen afleiden:
D1 = L1 - (R + T)TAN(A/2) (4) D2 = L2 - (R + T)TAN(A/2) (5)
Door vergelijkingen (4) en (5) in vergelijking (3) te substitueren, krijgen we het verband tussen BA en BD:
BA = 2(R + T)TAN(A/2) - BD (6)
En als de buighoek 90 graden is, wordt deze vergelijking vereenvoudigd tot:
BA = 2(R + T) - BD (7)
Deze vergelijkingen (6) en (7) bieden een handige methode voor het omrekenen van het ene algoritme naar het andere, waarbij alleen de materiaaldikte, buighoek/radius, enz. als parameters worden gebruikt.
Voor SolidWorks-gebruikers bieden deze vergelijkingen een directe methode voor het omzetten van buigaftrek naar buigtoeslag.
De waarde van de buigtoeslag kan gebruikt worden voor het volledige onderdeel of voor elke afzonderlijke bocht, of kan opgenomen worden in een tabel met buiggegevens.
De K-factor is een op zichzelf staande waarde die het buigen en ontvouwen van plaatmetaal in verschillende geometrische scenario's verklaart.
Het is ook een autonome waarde die wordt gebruikt om de buigtoeslag (Bending Allowance, BA) te berekenen onder verschillende omstandigheden zoals verschillende materiaaldiktes, buighoeken en radii.
Figuren 4 en 5 helpen de diepgaande definitie van de K-factor te verduidelijken.
Figuur 4
Figuur 5
We kunnen bevestigen dat er een neutrale as is in de dikte van het plaatwerkonderdeel. De plaat metaalmateriaal in deze neutrale as in het buiggebied wordt noch uitgerekt noch samengedrukt, wat betekent dat dit het enige gebied is dat niet vervormt tijdens het buigen.
Figuren 4 en 5 tonen de grens tussen de roze en blauwe gebieden.
Tijdens het buigen wordt het roze gebied samengedrukt en het blauwe gebied uitgerekt. Als de neutrale plaatlaag onvervormd blijft, blijft de lengte van de boog in het buiggebied gelijk, of het onderdeel nu gebogen of platgedrukt wordt.
Als gevolg hiervan moet de buigtoeslag (BA) gelijk zijn aan de lengte van de boog van de neutrale laag in het buiggebied van het plaatmetalen onderdeel, dat in groen is weergegeven in Figuur 4.
De positie van de neutrale laag van plaatmetaal is afhankelijk van de eigenschappen van een specifiek materiaal, zoals vervormbaarheid.
Er wordt aangenomen dat de afstand tussen de neutrale plaatwerklaag en het oppervlak "t" is, of de diepte vanaf het oppervlak van het plaatwerkdeel in het materiaal in de dikterichting.
Hierdoor kan de boogstraal van de neutrale laag worden uitgedrukt als (R + t). Met behulp van deze uitdrukking en de buigingshoek kan de booglengte van de neutrale laag (BA) worden berekend.
BA = Pi(R+T)A/180
Om de definitie van de plaatneutrale laag te vereenvoudigen en toepasbaar te maken op alle materialen, werd het concept van de K-factor geïntroduceerd.
De definitie van de K-factor is: het is de verhouding tussen de dikte van de neutrale laag van het plaatmateriaal en de totale dikte van het plaatmateriaal van het onderdeel. Met andere woorden, de K-factor wordt gedefinieerd als:
K = t/T
Daarom zal de waarde van K altijd binnen het bereik van 0 tot 1 liggen. Als een K-factor 0,25 is, geeft dit aan dat de neutrale laag zich op 25% van de totale dikte van het plaatmateriaal bevindt.
Als het 0,5 is, betekent dit dat de neutrale laag zich op 50% van de hele dikte bevindt, enzovoort.
Door de bovenstaande vergelijkingen te combineren, kan de volgende vergelijking (8) worden verkregen:
BA = Pi(R+K*T)A/180 (8)
Daarom zal de waarde van K altijd tussen 0 en 1 liggen.
Als een K-factor 0,25 is, betekent dit dat de neutrale laag zich op 25% van de dikte van het plaatmateriaal van het onderdeel bevindt.
Als het 0,5 is, betekent dit dat de neutrale laag zich op 50% van de hele dikte bevindt, enzovoort.
De oorsprong van de K-factor is terug te voeren op traditionele bronnen zoals leveranciers van plaatmaterialen, testgegevens, ervaring, handleidingen, enz.
In sommige gevallen kan de geleverde waarde echter niet worden uitgedrukt als een duidelijke K-factor, maar is het nog steeds mogelijk om de relatie ertussen te vinden.
Als bijvoorbeeld in een handleiding of literatuur de neutrale as wordt beschreven als "gepositioneerd op 0,445x de materiaaldikte vanaf het plaatoppervlak", kan dit worden geïnterpreteerd als een K-factor van 0,445, wat betekent dat k = 0,445.
Wanneer deze waarde van K in vergelijking (8) wordt gesubstitueerd, kan de volgende formule worden verkregen.
BA = A (0,01745R + 0,00778T)
Als vergelijking (8) met een andere methode wordt aangepast, de constante in vergelijking (8) wordt berekend en alle variabelen worden behouden, kan het volgende worden verkregen:
BA = A (0,01745 R + 0,01745 K*T)
Door de twee vergelijkingen te vergelijken, is het eenvoudig om te bepalen dat 0,01745 * k = 0,00778, en daarom kan k worden berekend op 0,445.
Er is ontdekt dat het SolidWorks systeem ook een algoritme voor buigtoleranties biedt voor specifieke materialen wanneer de buighoek 90 graden is. De berekeningsformule voor elk materiaal is als volgt:
Door vergelijking (7) te vereenvoudigen en de buighoek op 90 graden te zetten, kan de constante worden berekend en kan de vergelijking als volgt worden getransformeerd:
BA = (1,57 * K * T) + (1,57 *R)
Door de bovenstaande berekeningsformule te vergelijken, kan de waarde van K voor zacht messing of zacht koper worden verkregen als 1,57xk = 0,55, of K = 0,35.
Met dezelfde methode is het eenvoudig om de K-factorwaarden te berekenen voor de verschillende soorten materialen die hierboven zijn opgesomd.
Zoals eerder besproken, zijn er verschillende bronnen waaruit de K-factor waarde kan worden verkregen, zoals materiaalleveranciers, testgegevens, ervaring en handleidingen.
Om een nauwkeurig plaatmetaalmodel te maken met behulp van de K-factor methode, is het cruciaal om de juiste bron van K-factor te vinden die voldoet aan uw technische vereisten. Dit zorgt ervoor dat de resultaten van het fysische onderdeel zo nauwkeurig zijn als gewenst.
In sommige situaties kan het niet mogelijk zijn om nauwkeurige resultaten te verkrijgen door alleen een enkele K-factorwaarde te gebruiken, vooral als het nodig is om een breed scala aan buigingsscenario's te accommoderen.
In zulke gevallen is het aan te raden om de buigtoeslag (BA) waarde direct te gebruiken voor een enkele buiging van het hele onderdeel, of om een buigtabel te gebruiken om de verschillende BA, buigaftrek (BD), of K-factor waarden te beschrijven die corresponderen met verschillende A, R, en T waarden over het hele bereik.
Daarnaast kunnen vergelijkingen worden gebruikt om gegevens te genereren zoals de voorbeeldtabel voor buigingen die door SolidWorks wordt geleverd. Indien nodig kunnen cellen in de buigtabel ook worden aangepast op basis van experimentele of empirische gegevens.
De installatiemap van SolidWorks bevat buigtoeslagtabellen, buigaftrektabellen en K-factortabellen die naar wens kunnen worden bewerkt en aangepast.
Dit artikel geeft een uitgebreid overzicht van de gebruikelijke berekeningsmethoden en hun onderliggende principes die worden gebruikt bij het ontwerpen en vervaardigen van plaatwerkonderdelen.
Het behandelt de berekening van buigtoeslagen, buigaftrek en K-factoren en legt de verschillen tussen deze methoden en hun onderlinge relatie uit.
Het dient als een nuttig naslagwerk voor ingenieurs en technische professionals in de industrie.
Opmerking:
Als oprichter van MachineMFG heb ik meer dan tien jaar van mijn carrière gewijd aan de metaalbewerkingsindustrie. Door mijn uitgebreide ervaring ben ik een expert geworden op het gebied van plaatbewerking, verspaning, werktuigbouwkunde en gereedschapsmachines voor metalen. Ik denk, lees en schrijf voortdurend over deze onderwerpen en streef er voortdurend naar om voorop te blijven lopen in mijn vakgebied. Laat mijn kennis en expertise een aanwinst zijn voor uw bedrijf.
NL 
EN 
AR 
DE 
ES 
FR 
IT 
JA 
PT 
PT_BR 
RU 
KO