Heb je je ooit afgevraagd waarom een brug plotseling hevig kan gaan schudden of waarom een wijnglas breekt als een zanger een hoge toon aanslaat? In deze blog worden de fascinerende concepten van natuurlijke frequentie en resonantiefrequentie onderzocht en wordt onthuld hoe ze van invloed zijn op alles, van technische hoogstandjes tot alledaagse voorwerpen. Verwacht de geheimen achter deze trillingen te ontdekken en leer hoe ze onze wereld vormgeven.
In de dagelijkse analyse verwarren we vaak natuurlijke frequentie en resonantiefrequentie en denken we dat ze hetzelfde zijn.
In feite is dit niet rigoureus.
De eigenfrequentie is de prestatie van de natuurlijke eigenschappen van de constructie, terwijl de resonantiefrequentie de prestatie is van de reactie van de constructie onder externe krachten.
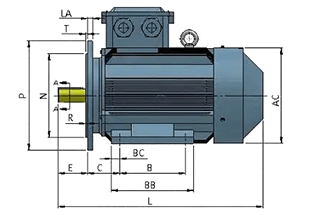
Een systeem met één vrijheidsgraad is een systeem waarbij de positie op elk moment volledig kan worden bepaald door slechts één gegeneraliseerde coördinaat. Eenvoudiger gezegd, de kracht die op een lichaam werkt, is slechts in één richting. De beweging van de pop in de figuur hieronder kan worden voorgesteld als een veer-massasysteem.
Een vereenvoudigd model van het veermassasysteem kan worden weergegeven in de volgende figuur.
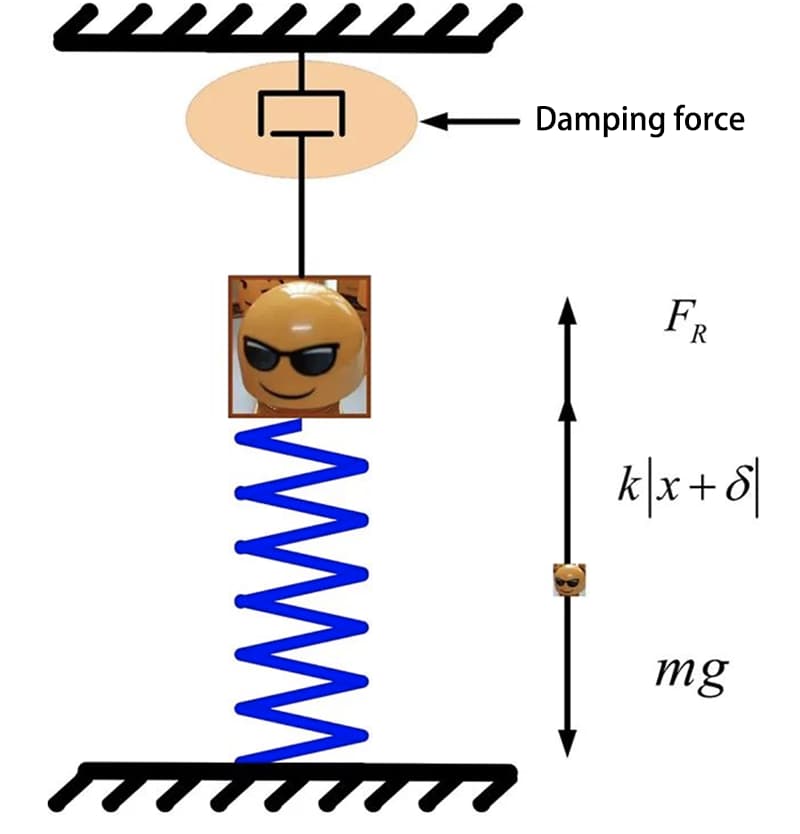
De statische evenwichtspositie van het ophaalblok wordt beschouwd als de coördinatenoorsprong en wordt als positief beschouwd als het blok verticaal naar beneden beweegt langs de richting van de veervervorming. De afstand tussen het blok en de evenwichtspositie kan worden voorgesteld als x, en de differentiële bewegingsvergelijking voor het blok kan worden uitgedrukt als:
Waarbij m de massa van het blok is, k de veerstijfheid, c de viscositeitscoëfficiënt, 2n=c/m de dempingsdempingscoëfficiënt en wanneer de dempingscoëfficiënt nul is, komt dit overeen met het ongedempte trillingssysteem.
Natuurlijke frequentie Pn:
De eigenfrequentie is alleen afhankelijk van massa en stijfheid en wordt niet beïnvloed door factoren zoals demping. Structurele grensverbindingen, materiaaleigenschappen, vorm en andere factoren kunnen de eigenfrequentie beïnvloeden, maar deze invloeden worden weerspiegeld in stijfheid en massa en zijn niet de uiteindelijke bepalende factoren.
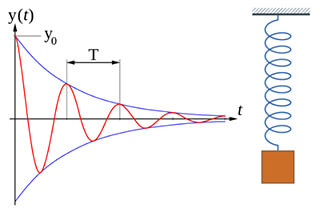
Vrije trilling is de trilling van het systeem zonder externe excitatie, en het bewegingsspoor is gerelateerd aan de begintoestand en de natuurlijke eigenschappen.
De gedwongen trilling verwijst naar de trilling die door het systeem wordt gegenereerd onder externe excitatie.
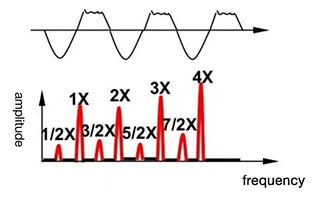
De externe excitatie is over het algemeen een periodieke of aperiodieke functie van de tijd, waarvan de eenvoudige harmonische excitatie de eenvoudigste is.
Laat de eenvoudige harmonische opwindende kracht zijn:
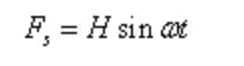
Waarbij H de amplitude van de opwindende kracht is en ω de hoekfrequentie van de opwindende kracht.
Wanneer het blok x afstand afwijkt van de evenwichtspositie, is de differentiaalvergelijking van de beweging van het blok
Waarbij h=H/m, de bovenstaande vergelijking de differentiaalvergelijking is van gedwongen trillingen van enkele vrijheidsgraad met viskeuze demping, wat een tweede orde constante coëfficiënt lineaire niet-homogene gewone differentiaalvergelijking is.
De bovenstaande vergelijking komt volledig overeen met de spanningsresponsie-uitdrukking voor capacitieve belasting die we hebben geleerd in de circuittheorie, wat een tweede-orde constante coëfficiënt lineaire niet-homogene gewone differentiaalvergelijking is.
De demping in het circuit hangt af van de weerstand, omdat de weerstand alleen energie verbruikt en niet opslaat.
Onder eenvoudige harmonische excitatie is de totale oplossing van de differentiaalvergelijking van een gedempt systeem als volgt:
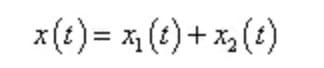
Waarbij x1 (t) een homogene oplossing is, die een vrije verzwakte trilling is;
Door het bestaan van demping zal het gedempte trillingsdeel na een bepaalde tijd verdwijnen.
De oplossing is dezelfde als die van vrije vibratie, dus die wordt hier niet herhaald.
Hier gaat het om de speciale oplossing x2 (t) gegenereerd door geforceerde trilling, die kan worden uitgedrukt als:
Onder hen,
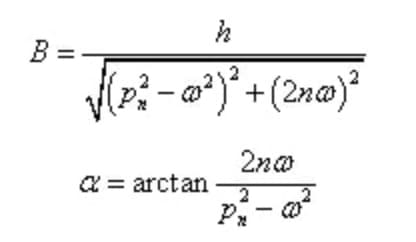
De amplitude en fasevertraging van de steady-state gedwongen trilling zijn onafhankelijk van de beginvoorwaarden, maar hangen alleen af van de eigenschappen van het systeem en de excitatie.
Stel de frequentieverhouding, dempingsverhouding en amplitudeversterkingscoëfficiënt in als:
De bovenstaande formule kan worden herschreven als:
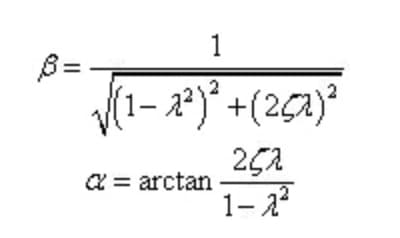
Op basis hiervan kunnen we de respons van het systeem onder de geforceerde trilling bepalen.
Voor een beter begrip kan de relatie tussen verschillende dempingsverhoudingen, frequentieverhoudingen en amplitudeversterkingscoëfficiënten worden geïllustreerd. De frequentie is verdeeld in drie gebieden: laagfrequent, middenfrequent en hoogfrequent. Zoals in de figuur te zien is, heeft de demping in zowel het laagfrequente als het hoogfrequente gebied een minimale invloed op de amplitudeversterkingscoëfficiënt. Het gedempte systeem kan dus vereenvoudigd worden als een ongedempt systeem om de berekening te vereenvoudigen.
De eigenfrequentie is een inherente eigenschap van de structurele eigenschappen van een systeem, uitsluitend bepaald door de massa en stijfheid, onafhankelijk van externe factoren zoals demping. In een systeem met n vrijheidsgraden bestaan er n verschillende natuurlijke frequenties, terwijl continue systemen een oneindig aantal natuurlijke frequenties bezitten.
Resonantie treedt op wanneer een externe excitatiefrequentie nauw overeenkomt of samenvalt met de natuurlijke frequentie van een systeem, waardoor de structuur met een aanzienlijk grotere amplitude gaat trillen. Dit fenomeen wordt weergegeven door de blauwe cirkel in de figuur hiernaast. De resonantiefrequentie benadert vaak de natuurlijke frequentie in licht gedempte systemen, maar kan hiervan afwijken in zwaar gedempte constructies.
In het systeemontwerp is het cruciaal om niet alleen de specifieke resonantiepiekfrequentie te vermijden, maar ook de omringende resonantieband, die overeenkomt met het tussenliggende frequentiegebied in de figuur. Deze voorzorgsmaatregel is nodig omdat de respons van het systeem binnen deze band aanzienlijk versterkt blijft. Ingenieurs moeten ervoor zorgen dat noch de normale werking van het systeem, noch externe prikkels van nabijgelegen apparatuur binnen dit kritieke bereik vallen.
Resonantie kan ingrijpende gevolgen hebben, zowel gunstig als nadelig. Negatieve effecten zijn bijvoorbeeld het instorten van hijsbalken, grondresonantie in helikopters, schade aan machines en infrasoon veroorzaakte structurele defecten. Omgekeerd wordt resonantie bewust gebruikt in muziekinstrumenten om de gewenste tonen en harmonischen te produceren.
Om de risico's van resonantie te beperken, gebruiken ontwerpers verschillende strategieën:
Het begrijpen en beheersen van resonantie is essentieel op gebieden variërend van civiele techniek en lucht- en ruimtevaart tot precisieproductie en het ontwerp van muziekinstrumenten. Geavanceerde analytische hulpmiddelen, zoals eindige-elementenanalyse en experimentele modale analyse, spelen een cruciale rol bij het voorspellen en karakteriseren van resonantiegedrag in complexe systemen.
Als oprichter van MachineMFG heb ik meer dan tien jaar van mijn carrière gewijd aan de metaalbewerkingsindustrie. Door mijn uitgebreide ervaring ben ik een expert geworden op het gebied van plaatbewerking, verspaning, werktuigbouwkunde en gereedschapsmachines voor metalen. Ik denk, lees en schrijf voortdurend over deze onderwerpen en streef er voortdurend naar om voorop te blijven lopen in mijn vakgebied. Laat mijn kennis en expertise een aanwinst zijn voor uw bedrijf.
NL 
EN 
AR 
DE 
ES 
FR 
IT 
JA 
PT 
PT_BR 
RU 
KO