Heb je ooit nagedacht over de krachten die spelen bij het buigen van een pijp? In dit artikel verkennen we de fascinerende wereld van buigmechanica. Onze deskundige werktuigbouwkundig ingenieur zal de belangrijkste concepten en berekeningen uiteenzetten en waardevolle inzichten verschaffen voor zowel professionals als enthousiastelingen. Maak je klaar om de wetenschap achter het maken van soepele, precieze buigingen in pijpen te ontdekken!
Het buigproces van pijpen is sterk geëvolueerd met de opkomst van verschillende industrieën zoals de auto-, motor-, fiets- en petrochemische industrie. Dit proces is essentieel voor het maken van nauwkeurige en duurzame bochten in pijpen die in deze sectoren worden gebruikt.
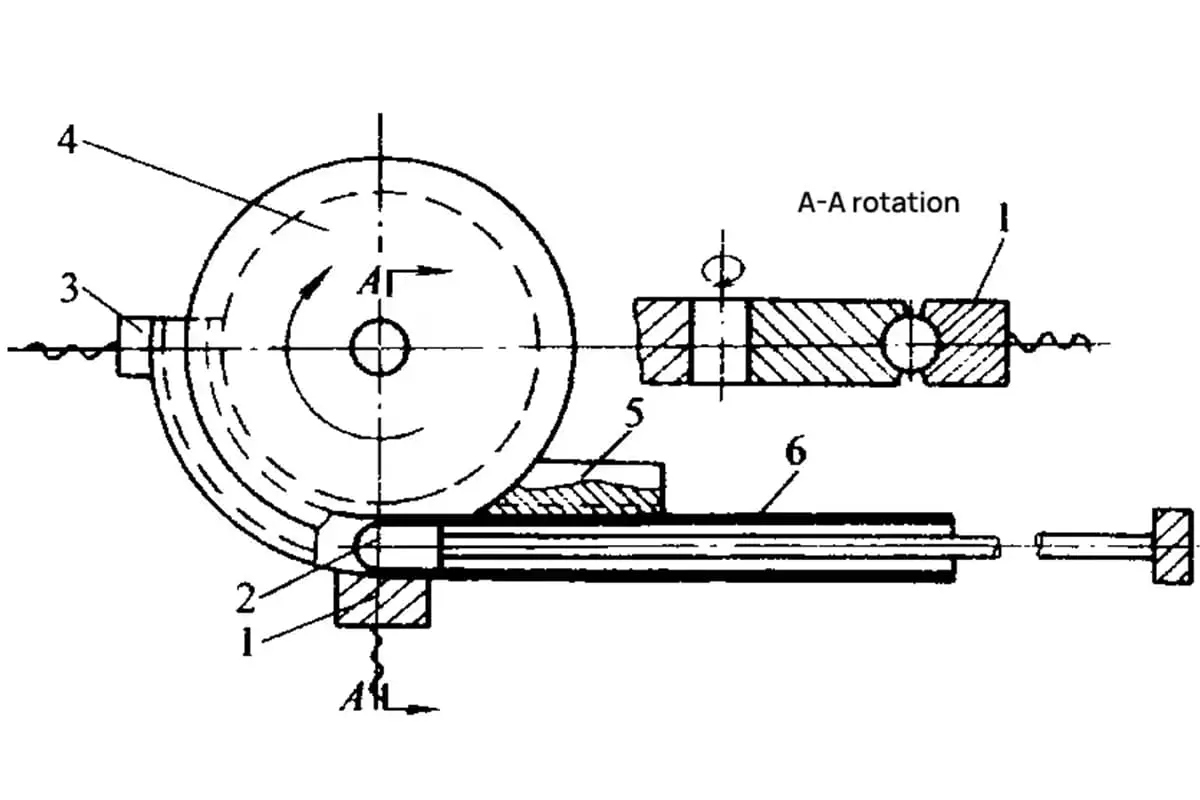
De figuren 6-19, 6-20, 6-21 en 6-22 geven respectievelijk de schematische diagrammen van de mallen voor het wikkelen, duwen, persen en rollen weer. Deze schema's illustreren de specifieke opstelling en onderdelen die bij elke buigmethode worden gebruikt en bieden een visuele referentie om het proces te begrijpen.
Door de buigmethoden voor pijpen te categoriseren op basis van de buigtechniek, temperatuur en het gebruik van vulmiddelen of doornen, kunnen we de juiste toepassingen en voordelen van elke methode beter begrijpen. Deze kennis is cruciaal voor het selecteren van het juiste buigproces voor specifieke industriële behoeften, waardoor efficiëntie en precisie in de productie worden gegarandeerd.

1- Drukblok
2-Kern Staaf
3- Klemblok
4- Buigvorm
5- Anti-rimpel blok
6- Pijp Blanco

1-Druk op Kolom
Sleeve met 2 gidsen
Blanco 3-buis
4-Buigende mal

1 matrijs
Blanco met 2 buizen
3 Zwaaiende Stoot

1-as
2,4,6-rollen
3-Actieve as
5-Staal pijp
Wanneer het buismateriaal wordt gebogen, wordt het materiaal aan de buitenkant van de vervormingszone uitgerekt en verlengd door de tangentiële spanning, terwijl het materiaal aan de binnenkant wordt samengedrukt en verkort door de tangentiële compressie.
Als de tangentiële spanning σθ en rek εθ continu verdeeld zijn over de dwarsdoorsnede van het buismateriaal, kunnen ze worden voorgesteld als vergelijkbaar met het buigen van het plaatmateriaal.
De rekzone aan de buitenzijde gaat over in de compressiezone aan de binnenzijde, met een neutrale laag op de overgang.
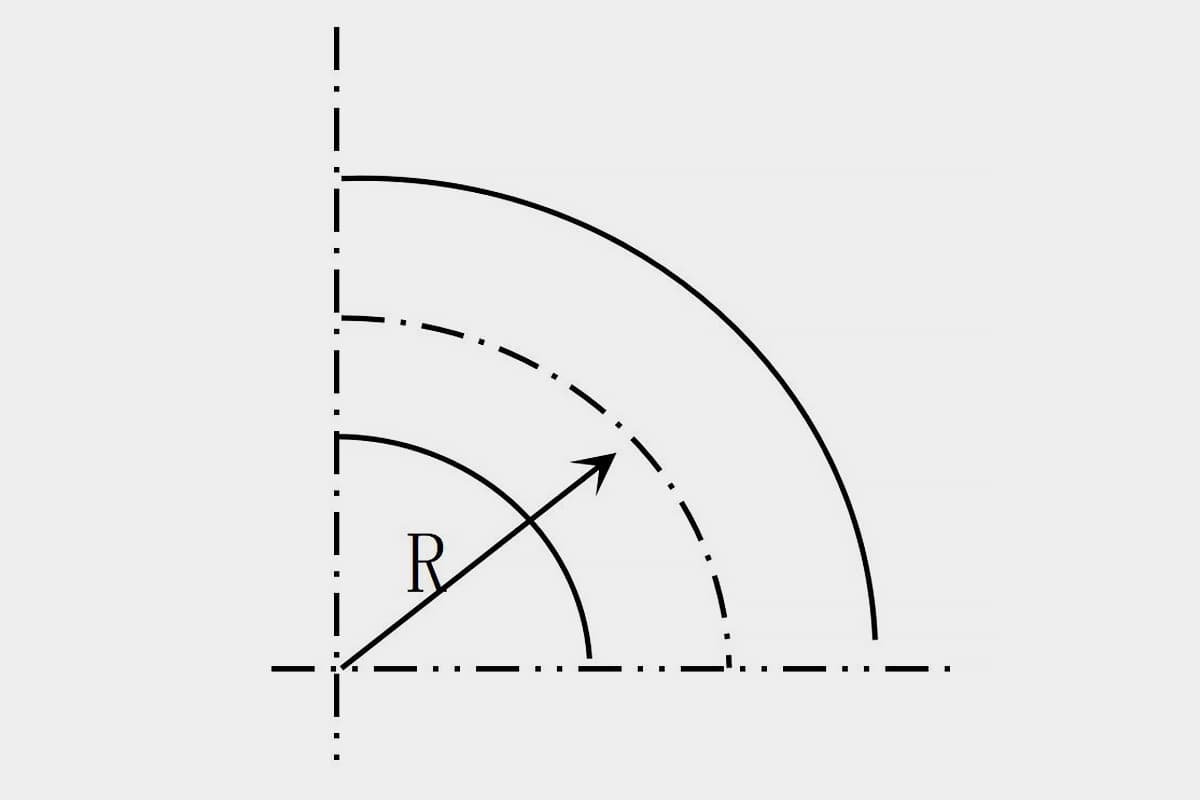
Om de analyse en berekening te vereenvoudigen, wordt er meestal van uitgegaan dat de neutrale laag samenvalt met de centrale laag van de buisdoorsnede en de positie ervan in de doorsnede kan worden weergegeven door de krommingsstraal (Afbeelding 6-23).
De mate van buigvervorming van het buismateriaal hangt af van de relatieve buigradius R/D en relatieve dikte t/D (R is de kromtestraal van de centrale laag van de pijpdoorsnede, D is de buitendiameter van de pijp, t is de wanddikte van de pijp).
Hoe kleiner de waarden R/D en t/D, hoe groter de mate van buigvervorming (d.w.z. R/D en t/D zijn te klein), de buitenwand van de buigneutrale laag wordt te dun en leidt zelfs tot breuk; de binnenwand van de pijp wordt dikker en wordt zelfs instabiel en rimpelig.
Tegelijkertijd wordt de vervorming van de dwarsdoorsnede (afplatting) ernstiger naarmate de mate van vervorming toeneemt.
Om de vormkwaliteit van het buismateriaal te garanderen, moet de mate van vervorming dus binnen het toegestane bereik worden gehouden.
De toegestane mate van vervorming bij het buigen van pijpen wordt de buigvormlimiet genoemd. De buigvervormingslimiet van het buismateriaal hangt niet alleen af van de mechanische eigenschappen van het materiaal en de buigmethode, maar houdt ook rekening met de gebruiksvereisten van de pijpfittingen.
Voor algemeen gebogen onderdelen is de maximale rek εmax geproduceerd op de positie het verst van de neutrale laag aan de buitenzijde van het buigvervormingsgebied van het buismateriaal mag de grenswaarde die is toegestaan door de plasticiteit van het materiaal niet overschrijden als voorwaarde voor het bepalen van de vervormingsgrens.
Dat wil zeggen, de grensbuigstraal rmin die kan worden gebogen in de binnenkant van het onderdeel onder de voorwaarde dat de buitenste oppervlaktelaag aan de buitenkant van het buigvervormingsgebied van het pijpdeel niet barst, wordt gebruikt als de vormingslimiet van het buigen van het pijpdeel.
rmin is gerelateerd aan de mechanische eigenschappen van het materiaal, de structurele afmetingen van de buisfittingen, de buigbewerkingsmethode en andere factoren.

a Krachtvoorwaarden
b Spanning-rekcondities
Het minimum buigradius voor verschillende buigprocessen zijn te vinden in Tabel 6-2.
Tabel 6-2 Minimale buigradius bij het buigen van pijpen (Eenheid: mm)
| Buigmethoden | Minimale buigradius |
| Buigen | (3~5)D |
| Wikkel buigen | (2~2.5)D |
| Rollen buigen | 6D |
| Buigen duwen | (2.5~3)D |
Opmerking: D staat voor de buitendiameter van de buis.
Voor de minimale buigradius van staal en aluminium buizen, raadpleeg Tabel 6-3.
Tabel 6-3 Minimale buigradius van stalen en aluminium buizen (Eenheid: mm)
| Buitendiameter van de pijp | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 |
| Minimale buigradius | 8 | 12 | 16 | 20 | 28 | 32 | 40 | 45 | 50 | 56 |
| Buitendiameter van de pijp | 24 | 28 | 30 | 32 | 35 | 38 | 40 | 44 | 48 | 50 |
| Minimale buigradius | 68 | 84 | 90 | 96 | 105 | 114 | 120 | 132 | 144 | 150 |
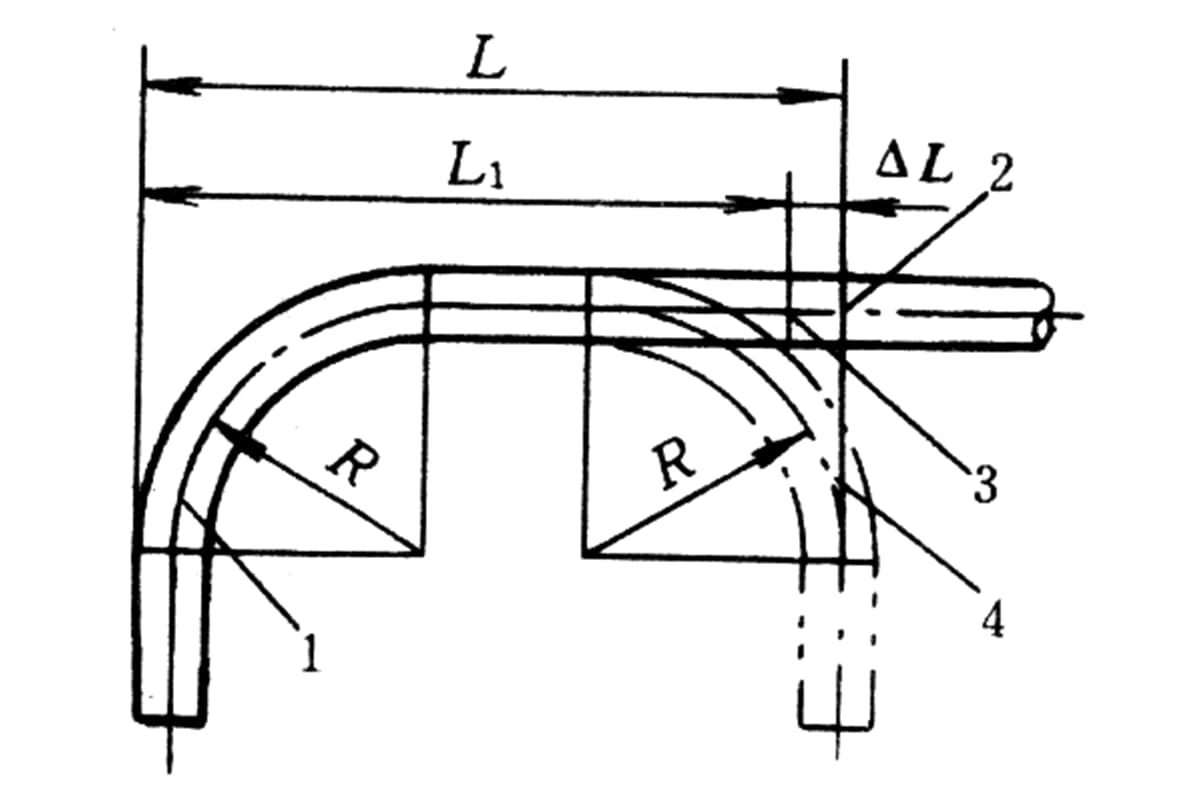
Tijdens het buigen van de pijp is vervorming van de dwarsdoorsnede onvermijdelijk.
Het materiaal aan de buitenkant van de neutrale laag ondergaat tangentiële trekspanning, waardoor de buiswand dunner wordt; het materiaal aan de binnenkant van de neutrale laag ondergaat tangentiële drukspanning, waardoor de buiswand dikker wordt.
Het materiaal aan de buitenste en binnenste zijden van het buigvervormingsgebied ondergaat de grootste tangentiële spanning, vandaar dat daar de grootste veranderingen in de wanddikte van de pijp optreden (fig. 6-24).
Bij buigen met vulstoffen of kernstaven kan de dwarsdoorsnede in principe een cirkelvorm behouden, maar verandert de wanddikte. Bij niet-ondersteund vrij buigenOf het nu de binnenrand of de buitenkant is, de cirkelvormige buisdoorsnede wordt elliptisch (fig. 6-24a, b).
Bovendien wordt de binnenrand onstabiel en rimpelig naarmate de mate van buigvervorming toeneemt (d.w.z. de buigradius neemt af). In het geval van vierkante buizen in ondersteunde buiging (fig. 6-24c, d) verandert de doorsnede in een trapeziumvorm.

De ellipticiteit wordt vaak gebruikt in de productie om veranderingen in de cirkelvormige dwarsdoorsnede van een pijp te meten.
Ellipticiteit= Dmax-Dmin/D ×100% (6-21)
In deze formuleDmax is de maximale buitendiameter gemeten in elke richting van dezelfde doorsnede van de buis na buigen, en Dmin is de minimale buitendiameter gemeten in elke richting van dezelfde doorsnede van de buis na buigen.
Figuur 6-25 is een ellipticiteitsplot, die de verandering van ellipticiteit weergeeft die overeenkomt met de dimensieloze kromming R0/R (R0 is de buitenstraal van de pijp, R is de krommingsstraal van de middelste laag van het buigsegment) op een logaritmische coördinaat, weergegeven als een familie van rechte lijnen met de verhouding t/R0 als parametervariabele.
Zoals te zien is in de figuur, is de ellipticiteit van de dwarsdoorsnede groter naarmate de mate van buiging groter is.
Daarom wordt ellipticiteit in de productie vaak gebruikt als een belangrijke index om de kwaliteit van gebogen buizen te inspecteren. Afhankelijk van de verschillende gebruiksprestaties van gebogen buismaterialen, variëren ook de vereisten voor hun ellipticiteit.
Voor gebogen pijpcomponenten die worden gebruikt in industriële pijpleidingprojecten is de hogedrukpijp bijvoorbeeld niet groter dan 5%; middeldruk- en lagedrukpijpen zijn 8%; aluminium pijpen zijn 9%; en pijpen van koperlegeringen en aluminiumlegeringen zijn 8%.

Vervorming van de doorsnedevorm kan de doorsnede verkleinen, waardoor de weerstand tegen vloeistofstroming toeneemt en kan ook de functionele prestaties van de buis in de constructie beïnvloeden.
Daarom moeten er tijdens het buigproces van de pijp maatregelen worden genomen om de vervorming binnen het vereiste bereik te houden.
Effectieve methoden om vervorming van de dwarsdoorsnede te voorkomen zijn:
1) Ondersteun de doorsnede met een doorn in het buigvervormingsgebied om vervorming van de doorsnede te voorkomen.
Voor verschillende buigprocessen moeten verschillende soorten opspandoorns worden gebruikt. Stijve opspandoorns worden vaak gebruikt bij buigen en wikkelen, en de kop van de opspandoorn is halfrond of heeft een andere gebogen oppervlaktevorm.
Of een doorn nodig is tijdens het buigen en wat voor soort doorn je moet gebruiken, kun je bepalen aan de hand van Figuur 6-26 en Figuur 6-27.

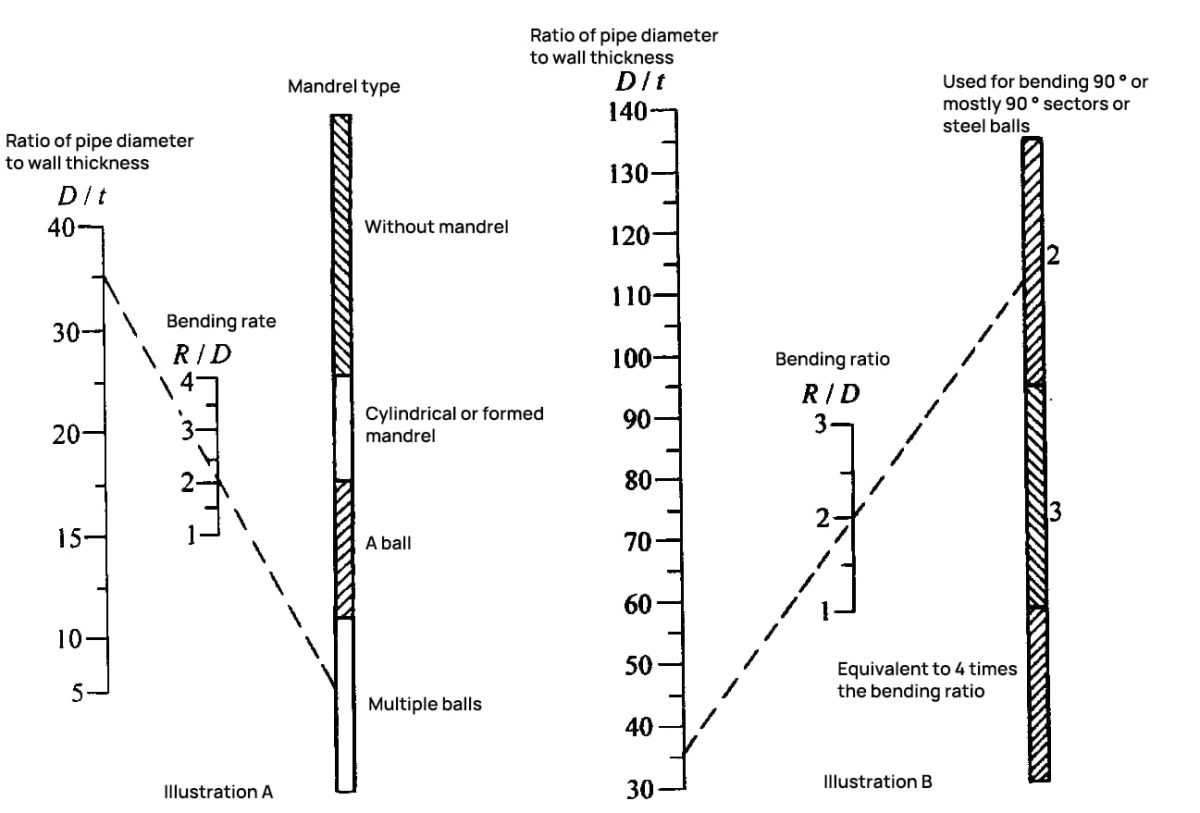
2) Het vullen van de gebogen buis met korrelige media, vloeibare media, elastische media of legeringen met een laag smeltpunt kan ook de kernstaaf vervangen om vervorming van de doorsnede te voorkomen. Deze methode is relatief eenvoudig toe te passen en wordt veel gebruikt, meestal voor productie op kleine tot middelgrote schaal.
3) Op het oppervlak van de mal dat in contact komt met het buismateriaal, een groef is zo gemaakt dat hij overeenkomt met de vorm van de doorsnede van het buismateriaal, waardoor de druk op het contactoppervlak wordt verminderd en vervorming van de doorsnede wordt voorkomen. Dit is een zeer effectieve maatregel om vervorming van de doorsnede te voorkomen.
4) De methode van het gebruik van de tegenvervormingsmethode om de verandering in de buisdoorsnede te controleren (Afbeelding 6-28) wordt vaak gebruikt in het kernloze buigproces op de pijpenbuiger. Het kenmerk van deze methode is de eenvoudige structuur en wordt daarom veel gebruikt.
Het gebruik van tegenvervorming bij kernloos buigen betekent dat de lege buis vooraf een bepaalde hoeveelheid omgekeerde vervorming krijgt. Na het buigen wordt de vervorming in verschillende richtingen gecompenseerd, waardoor de lege buissectie in principe cirkelvormig blijft om aan de elliptische eisen te voldoen, waardoor de kwaliteit van de gebogen buis gewaarborgd blijft.

1-Buigvorm
2-Klemblok
3-rollen
4-Gids Wiel
5-pijps blanco
De doorsnedevorm van de anti-vervormingsgroef zoals getoond in Figuur 6-29, de grootte van de anti-vervormingsgroef is gerelateerd aan de relatieve buigradius (de krommingsradius van de centrale laag, de buitendiameter van de pijp). Zie tabel 6-4.
Tabel 6-4 Afmetingen van de anti-vervormingsgroef
| Relatieve buigradius R/D | R1 | R2 | R3 | H |
| 1.5~2 | 0.5D | 0.95D | 0.37D | 0.56D |
| >2~3.5 | 0.5D | 1.0D | 0.4D | 0.545D |
| ≥3.5 | 0.5D | - | 0.5D | 0.5D |

1-Buigvorm
2 Anti-vervormingsrol
De verandering in buisdikte hangt voornamelijk af van de relatieve buigradius R/D en de relatieve dikte t/D. Bij de productie is de minimale wanddikte tmin op de buigbuitenzijde en de maximale wanddikte tmax aan de binnenkant kan meestal worden geschat met de volgende formule:

In de formule,
Het dunner worden van buismateriaal vermindert de mechanische sterkte en bruikbaarheid van de fittingen. Daarom wordt bij de productie de mate van wanddunning vaak gebruikt als technische index om de verandering in wanddikte te meten en zo de bruikbaarheid van de fittingen te garanderen.
Dunner wordende buiswand = t-tmin/t×100%
In de formule:
De prestaties van buismaterialen variëren en er zijn verschillende eisen voor de reductiesnelheid van de wanddikte.
Voor pijpfittingen die gebruikt worden in de industriële pijptechniek is de hogedrukpijp bijvoorbeeld niet groter dan 10%; de middeldruk- en lagedrukpijp niet groter dan 15% en niet kleiner dan de berekende ontwerpwanddikte.
Maatregelen om het dunner worden van de pijpdikte te verminderen zijn onder andere:
1) Verminder de numerieke waarde van de trekspanning die aan de buitenkant van de neutrale laag wordt opgewekt. Bijvoorbeeld door de methode van weerstandsverhitting ter plaatse te gebruiken om de vervormingsweerstand van de metaalmateriaal binnen de neutrale laag, waardoor de vervorming meer geconcentreerd is in het samengedrukte deel en het doel wordt bereikt om het spanningsniveau van het trekdeel te verlagen.
2) Verander de spanningstoestand van de vervormingszone en verhoog de component van de drukspanning. Zo kan het veranderen van buigen naar duwen het defect van overmatig dunner worden van de buiswand fundamenteel verhelpen.
De berekening van het buigmoment van het buismateriaal vormt de basis voor het bepalen van de energieparameters van de buigmachine.
Volgens de analyse van de plastische mechanica theorie wordt de theoretische uitdrukking van het buigmoment wanneer het buismateriaal uniform gebogen is als volgt afgeleid:
Buigmoment van buismateriaal:
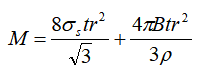
In de formule:
Het werkelijke buigmoment van het buismateriaal hangt niet alleen af van de eigenschappen van het buismateriaal, de vorm en grootte van de dwarsdoorsnede, de buigradius en andere parameters, maar is ook sterk gerelateerd aan de buigmethode en de structuur van de gebruikte mal.
Daarom is het op dit moment onmogelijk om al deze factoren in een berekeningsformule weer te geven en kunnen er alleen schattingen worden gemaakt in de productie.
Het buigmoment van het buismateriaal kan worden geschat met de volgende formule:

In de vergelijking,
De coëfficiënt µ is niet de wrijvingscoëfficiënt; de waarde ervan hangt af van de oppervlaktegesteldheid van de pijp, de buigmethode, vooral of er een doorn wordt gebruikt, het type en de vorm van de doorn en zelfs verschillende factoren die te maken hebben met de positie van de doorn.
In het algemeen kan bij gebruik van een starre doorn zonder smering een waarde van 5 tot 8 worden genomen; bij gebruik van een starre scharnierende doorn kan een waarde van µ=3 worden genomen.
De dwarsdoorsnede van de anti-vervormingsgroef wordt getoond in Figuur 6-29.
De afmetingen van de anti-vervormingsgroef zijn gerelateerd aan de relatieve buigradius (de krommingsradius van de centrale laag, de buitendiameter van de buis).
Zie Tabel 6-4.
Tabel 6-4 Afmetingen van de anti-vervormingsgroef
| Relatieve buigstraal R/D | R1 | R2 | R3 | H |
| 1.5~2 | 0.5D | 0.95D | 0.37D | 0.56D |
| >2~3.5 | 0.5D | 1.0D | 0.4D | 0.545D |
| ≥3.5 | 0.5D | - | 0.5D | 0.5D |

1-Buigvorm
2 Anti-vervormingsrol
De verandering in buisdikte hangt voornamelijk af van de relatieve buigradius R/D en de relatieve dikte t/D.
In de productie is de minimale wanddikte tmin aan de buitenkant van de bocht en de maximale wanddikte tmax aan de binnenkant kan over het algemeen worden geschat met de volgende formule:

In de formule:
Het dunner worden van het buismateriaal vermindert de mechanische sterkte en prestaties van de buisfittingen. Daarom wordt de mate van uitdunning in de productie vaak gebruikt als een technische indicator om de verandering in wanddikte te meten, om aan de prestatievereisten van de buisfittingen te voldoen.
Snelheid van buiswanddunning = (t-tmin)/t×100%
In de formule:
Verschillende prestaties van het buismateriaal vereisen verschillende verdunningspercentages. Voor pijpfittingen die in de industriële pijpleidingbouw worden gebruikt, mag de hogedrukpijp bijvoorbeeld niet dunner zijn dan 10%; de middel- en lagedrukpijpen mogen niet dunner zijn dan 15% en mogen niet dunner zijn dan de wanddikte van de ontwerpberekening.
Maatregelen om het dunner worden van de buisdikte te verminderen zijn onder andere:
1) Het verminderen van de numerieke waarde van de trekspanning die aan de buitenkant van de neutrale laag wordt opgewekt, zoals het aannemen van de methode van weerstand plaatselijk verwarmen, het verminderen van de vervormingsweerstand van het metaalmateriaal aan de binnenkant van de neutrale laag, waardoor de vervorming meer geconcentreerd wordt in het samengedrukte deel, waardoor het doel van het verminderen van het spanningsniveau van het trekdeel wordt bereikt.
2) De spanningstoestand van de vervormingszone veranderen en de component van de drukspanning verhogen. Zo kan het veranderen van buigen naar duwen het defect van overmatig dunner worden van de buiswand fundamenteel verhelpen.
De berekening van het buigmoment van de buis is de basis voor het bepalen van de vermogensparameters van de pijpbuigmachine. Volgens de analyse van de theorie van de plastische mechanica wordt de theoretische uitdrukking van het uniforme buigmoment van de buis als volgt afgeleid:
Buigmoment van de buis:

In de formule:
Het werkelijke buigmoment van het buismateriaal hangt niet alleen af van de prestaties van het buismateriaal, de vorm en grootte van de doorsnede, de buigradius en andere parameters, maar heeft ook veel te maken met de buigmethode en de structuur van de gebruikte mal.
Daarom is het momenteel onmogelijk om alle factoren in een berekeningsformule uit te drukken en kunnen alleen schattingen worden gemaakt bij de productie.
Het buigmoment van het buismateriaal kan worden geschat met de volgende formule:

In de formule:
De coëfficiënt is niet de wrijvingscoëfficiënt µ, de waarde hangt af van de oppervlaktegesteldheid van de pijp, de buigmethode en vooral of er een doorn wordt gebruikt, het type en de vorm van de doorn en zelfs verschillende factoren die te maken hebben met de positie van de doorn.
Over het algemeen kan bij gebruik van een starre doorn zonder smering worden uitgegaan van =5 tot 8; bij gebruik van een starre scharnierende doorn kan worden uitgegaan van µ=3.
Buizenwalsen is een speciaal vormgevingsproces ontwikkeld uit traditionele stempelen flens- en halsprocessen. Het is een vervormingsproces waarbij de rand van de buismond plaatselijk wordt gebogen door axiale druk uit te oefenen op het buisstuk door de mal.
Het gebruik van deze technologie om onderdelen te maken heeft een reeks voordelen zoals eenvoudige technologie, minder processen, lage kosten en goede kwaliteit. Het kan zelfs onderdelen produceren die moeilijk te maken zijn met andere stansmethoden.
Dit proces wordt veel gebruikt in verschillende industriële sectoren, zoals de auto- en luchtvaartindustrie.
Er zijn twee basismanieren om buizen te draaien, namelijk buitenwalsen en binnenwalsen (Afbeelding 6-30).

a, b buitenwaartse rol;
c, d binnenwaartse rol
1 lege buis
2-stroomgeleidingsring
3-kegel schimmel
4-Ronde rand schimmel
Naar buiten rollen: De lege buis wordt onder axiale druk van binnen naar buiten gedraaid, waardoor de omtrek na het vormen toeneemt.
Naar binnen rollen: De lege buis wordt van buiten naar binnen gewalst, waardoor de omtrek na het vormen wordt verkleind.
Het walsproces kan niet alleen effectief verschillende soorten buisvormige dubbelwandige of meerlaagse onderdelen vormen, maar ook convexe bodembekers, stapbuizen, speciaal gevormde buizen en semi-dubbele buizen, ringvormige dubbelwandige cilinders, holle dubbelwandige moeren, warmtewisselaars, geluiddempers voor auto's, golfgeleiderbuizen in de elektronica-industrie, enz. verwerken.
Momenteel worden deze onderdelen over het algemeen verwerkt door meervoudig stansen en lasmethodendie moeilijk en duur zijn en er slecht uitzien.
Het gebruik van het walsproces garandeert de betrouwbaarheid van het onderdeel, is licht van gewicht en bespaart grondstoffen.

Volgens de gegevens zijn momenteel veel metalen materialen kan worden gevormd op de mal in verschillende rollende methoden, zoals aluminiumlegering, koper en koperlegeringen, laag koolstofstaal, austenitisch roestvast staal, enz. Buizen met alle geluidspecificaties kunnen met succes worden gewalst tot dubbellaagse buizen.
Rolvorming, vergeleken met andere vormprocessenheeft een complexer vervormingsproces, dat uitwaaieren, krullen, walsen en hun onderlinge omzetting omvat.
Er zijn verschillende mallen om dit vormproces te realiseren, waarvan de eenvoudigste en meest gebruikte conische mallen en filetmallen zijn.
1. Conische buis walsvorm
De structuur van de conische buisrolvorm wordt getoond in Figuur 6-32. Deze matrijsstructuur is eenvoudig en verschillende specificaties van buizen kunnen worden gevormd op één set mallen, wat moeilijk te bereiken is met andere mallen voor het vormen van buizen.
Ook als voorvormproces voor het vormen van precisiebuisrollen wordt het kegelvormproces veel gebruikt.

een buis die Vormstructuur omdraait
b Procesparameters voor het omkeren van conische buizen
1 - Perskop
2 - buis Billet
3 - Kegelvorm
Tijdens het buisdraaiproces wordt het ene uiteinde van de blinde buis op een conische matrijs geplaatst, terwijl het andere uiteinde wordt onderworpen aan axiale druk van de persschuif om de blinde buis te kunnen draaien.
Bij het ontwerpen van deze type matrijsis de halve kegelhoek α van de matrijs de meest kritieke parameter.
De grootte van α bepaalt niet alleen de haalbaarheid van het draaien van de buis, maar beïnvloedt ook de geometrische afmetingen van het draaien van de buis, namelijk de coëfficiënt voor het draaien van de buis K(K=D/D1, waarbij D en D1 respectievelijk de buitendiameter van de blinde buis en de buitendiameter van het draaien van de buis zijn).
Er bestaat duidelijk een kritische halve tophoek α0, en het draaien kan alleen normaal worden uitgevoerd als de halve tophoek α≥ α0.
µ, H, Golubnov afgeleid op basis van het principe van hoofdspanning:

Rekening houdend met de invloed van materiaalversterking en de stijfheid van het uitlopende uiteinde, kan de bovenstaande formule als volgt worden aangepast:

In de formule:

Voor een 42mm 3A21 aluminium buis, berekend met bovenstaande formule, is de hoek 55° - 60°.
Empirische tests tonen aan dat wanneer de hoek α≥60° (α≈68°) is, het omkeren van de buis soepel kan verlopen. Op dat moment is de axiale druk het kleinst.
Bij een hoek van 55° - 60° krult het uiteinde van de lege buis om, maar komt niet in de omslagfase. Bij een hoek α<55° krult het buisuiteinde alleen op de conusmatrijs en krult het niet om.
Tijdens het omkeren van de kegel schuift het uiteinde van de buis gemakkelijk, waardoor het omgeklapte deel van de buis uit de as ligt ten opzichte van de oorspronkelijke buis en er een axiale buiging ontstaat tijdens het omkeren.
Het is moeilijk om een dubbellaags geflipt buisdeel te krijgen dat voldoet aan de kwaliteitseisen voor assemblage. Vandaar dat een rond De hoekverdraaiingsmatrijs werd ontwikkeld op basis van de kegelmatrijs.
2. Ronde hoek omslagmatrijs
De matrijs voor het omkeren van de ronde hoek gebruikt het werkende deel van de matrijs, dat een straalcirkel is, om het axiaal samengeperste buisuiteinde te dwingen om langs zijn boog te vervormen om het omkeren van de buis te bereiken.
Figuur 6-33 toont een schematisch diagram van een blinde buis met een dikte van t en een gemiddelde diameter van D, die gewalst wordt op een ronde hoekmatrijs met een straal van r, onder axiale belasting krult het buisuiteinde omhoog langs de boog van de matrijs om een gewalst buisstuk te krijgen met een diameter van D1.
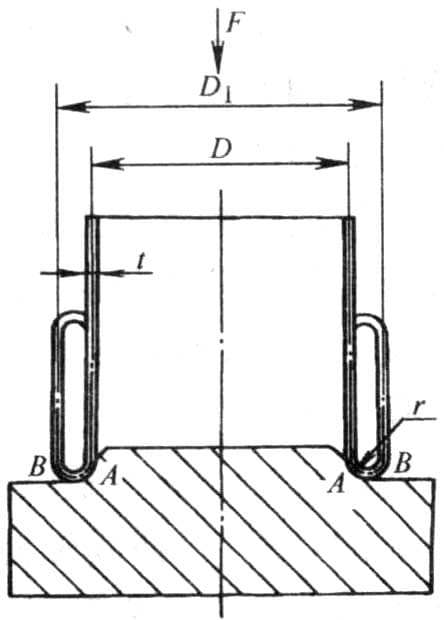
De belangrijkste parameter bij het ontwerpen van een flensmatrijs met ronde hoek is de straal r van de hoek van de matrijs. Deze bepaalt niet alleen de geometrische afmetingen van het geflensde onderdeel, maar beïnvloedt ook de grootte van de flenskracht.
Voor de 3A21 gegloeid aluminium buis van het type Φ41×1, tonen zowel de theoretische analyse als de experimentele resultaten aan dat de kritische afschuiningstraal (minimale afschuiningstraal) voor buisinversie-instabiliteit ongeveer 2 mm is; de optimale afschuiningstraal is ongeveer 3 mm; de maximale afschuiningstraal is ongeveer 4 mm.
Dit geeft aan dat de stabiliteit en kwaliteit van buisomkering onder axiale belasting afhangen van de afschuinstraal r. Als r kleiner is dan een bepaalde kritische waarde, krult het buiseinde niet langs de boog van de matrijs; als r te groot is, breekt het buiseinde en kan het niet succesvol worden omgekeerd. Alleen als r binnen een geschikt bereik ligt, kan de buisomkering worden gerealiseerd.
Gelijkaardig aan het naar buiten krullen van het buismateriaal, kan het naar binnen krullen van de buis ook uitgevoerd worden op de kegelvorm en de hoekvorm (Figuur 6-34).
Vergeleken met andere vormingsprocessen is het gevoelig voor instabiliteit. Omdat tijdens het naar binnen krullen, de diameter van de buis afneemt na vervorming, de buiswand dikker wordt, de kracht van de buisomkering toeneemt, wat problemen oplevert bij het krullend vormen.
Volgens theoretische berekeningen en de praktijk kan het krulproces soepel verlopen als de kritische halve kegelhoek β van de buisinversiekegelvorm ≥120° is. In de productie wordt de waarde meestal genomen als β≥120°~125°, rp≈4mm.
Het buiskrulproces kan alleen plaatsvinden als de voor het krullen benodigde belasting kleiner is dan de axiale instabiliteitsgrens. Aangezien de krulvormbelasting grotendeels afhangt van de geometrische parameters van de mal, hangt deze in termen van de hoekmal af van de hoekradius r.
Daarom kan een haalbaar gebied voor krulvorming worden bepaald (Afbeelding 6-35).

een conische matrijs
b Afgeronde matrijs

In Figuur 6-35 is te zien dat het gebied voor inwendig walsen vrij klein is en dat de walsbelasting numeriek hoger is dan die van uitwendig walsen en bijna 50% bereikt.
Bestaande gegevens tonen aan dat zowel nationaal als internationaal de optimale procesparameters voor uitwendig walsen theoretisch en praktisch zijn bestudeerd en dat de relatie is ontdekt tussen de minimale axiale drukspanning die nodig is voor volledig walsen en de binnendiameter, buitendiameter en wanddikte van het buismateriaal.
Tijdens het uitwendig walsen van buismaterialen is de verandering in wanddikte niet significant.
Tijdens het inwendig walsen zorgt de omtrekdrukspanning er echter voor dat de wanddikte bij de mal voortdurend toeneemt tot deze een constante waarde bereikt, die 1,5 keer de oorspronkelijke dikte kan zijn. Daarom is er een grotere axiale belasting nodig om het inwendig walsen te voltooien.
De twee bovengenoemde soorten walsen (traditioneel walsen) hebben een aantal tekortkomingen:
1. Het begin van de tweede laag van de buiswand is niet evenwijdig aan de oorspronkelijke buiswand, maar draait altijd naar de binnenholte van de dubbelwandige buis;
2. Er is een bepaalde afstand tussen de nieuwe buiswand en de oorspronkelijke buiswand, die afhangt van de relatieve diameter (D/t) van het oorspronkelijke buismateriaal;
3. Bij inwendig walsen is de tweede laag van de buiswand aanzienlijk dikker, wat weer leidt tot een toename van de axiale druk tijdens het walsen.
De problemen die zich voordoen in de bovengenoemde processen zijn te wijten aan het vervormingsmechanisme, dat de geometrische vorm van de verkregen buizen beperkt, vooral de slechte stabiliteit en de hoge moeilijkheidsgraad van het interne walsproces, dat moet worden verbeterd.
Daarom is de trekspanningsrolvormmethode voor het inwendig walsen van buismaterialen ontstaan.
Het kenmerk van de trekspanningsrolvormmethode is dat het walsen stopt in de eerste fase van het inwendig walsen van het buismateriaal en dat de gewalste rand een omgekeerde buiging krijgt, waardoor hij naar de buitenkant van de holte wordt geleid.
Vervolgens zorgt de trekkracht die op de omgekeerde buigrand op de binnenwand inwerkt er door de bolle mal voor dat de blinde buis inwendig rolt in plaats van door de axiale druk die op de buitenwand inwerkt, waardoor de axiale druk afneemt.
Dit proces kan een grotere binnenwandhoogte, constante wanddikte en hogere productnauwkeurigheid bereiken.
De trekspanningsrolvormmethode heeft het toepassingsgebied van het interne rolvormproces uitgebreid, zoals de productie van pijpverbindingen, rollagerstoelen en andere (Afbeelding 6-36).

De trekspanningsrolvormmethode kan worden verdeeld in drie stappen zoals getoond in Figuur 6-37.
In de eerste stap (Afbeelding 6-37a) eindigt het traditionele binnenwalsen wanneer de rand van de buis een kwart van de filetmatrijs verlaat.
Op dat moment vormt de afstand tussen de rand van de buis en de binnenwand van de matrijs de radiale ondersteuning van het eindproduct en moet gelijk zijn aan de vereiste breedte.
In de tweede stap (Afbeelding 6-37b) daalt de bolle matrijs met vlakke bodem, waardoor de rand van de buis flensvormig wordt (vergelijkbaar met de gatflenzen van de plaat). De opening tussen de bolle matrijs en de matrijs van de binnenste rol wordt bepaald door de buiswanddikte (de wanddikte van de binnenste rol wordt iets vergroot).
In de derde stap (Figuur 6-37c, d) gaat de vormende bolle matrijs omhoog, waardoor de rand van de buis naar binnen rolt en de tweede laag buiswand ontstaat onder druk van de vormende bolle matrijs.
Zoals te zien is in de figuur, werkt de vormende bolle matrijs op de rand van de buis met trekspanning en niet met drukspanning op de hele buis.
Er is geen relatief glijden tussen de matrijs en het vervormde materiaal en er wordt een afstand bewaard tussen de vormladingen, waardoor de axiale drukspanning op het transmissiegebied van de buis wordt verminderd en instabiliteit wordt voorkomen.
Daarom heeft trekspanningswalsen een grotere vrijheid bij het kiezen van de walsradius, terwijl de matrijsradius een belangrijke procesparameter is bij traditionele bewerkingsprocessen (Afbeelding 6-35).

Voorwaarden voor het succesvol uitvoeren van dit proces:
FPerforatiegat≥FRolling (6-22)
De ponskracht omvat drie componenten (symbool in Figuur 6-37d): de belasting die plastische vervorming van het materiaal veroorzaakt bij straal rP; de belasting die nodig is om de wrijving bij hoekra tussen de pons en de rand van de buis te overwinnen; de belasting die nodig is voor het buigen en ontbuigen van het randmateriaal van de radiale naar de axiale positie.
In de analytische uitdrukking is σ1 wordt gebruikt om de vervormingsspanning van de binnenwand weer te geven.
Dan,

Rolvorming omvat twee aspecten: de belasting die nodig is voor het rollen van materiaal naar verschillende posities van kromtestralen en de belasting die nodig is voor het buigen en terugkaatsen van het begin tot het einde van de vervormingszone.
In de analyse wordt σ0 wordt gebruikt om de vervormingsspanning van de buitenwand weer te geven, en σm vertegenwoordigt de gemiddelde plastische vervormingsspanning in de vervormingszone.

Conclusie:
De methode om de buis te vormen door rollen onder trekspanning is bewezen door experimenten.
Hoewel er twee voorbereidingsfasen nodig zijn voordat het walsen begint en herkristallisatiegloeien waar nodig is, heeft het de volgende voordelen in vergelijking met het traditionele walsproces:
1) De gerolde rand draait naar het midden van de holte, waardoor het gemakkelijk te coördineren is met andere onderdelen, zoals de kogel lager zetels.
2) De rolbelasting is aanzienlijk verminderd.
3) De vervormingsgrens is sterk verbeterd en producten met een kleinere rolstraal kan worden verkregen.
4) Er is geen wrijving en smering is niet nodig.
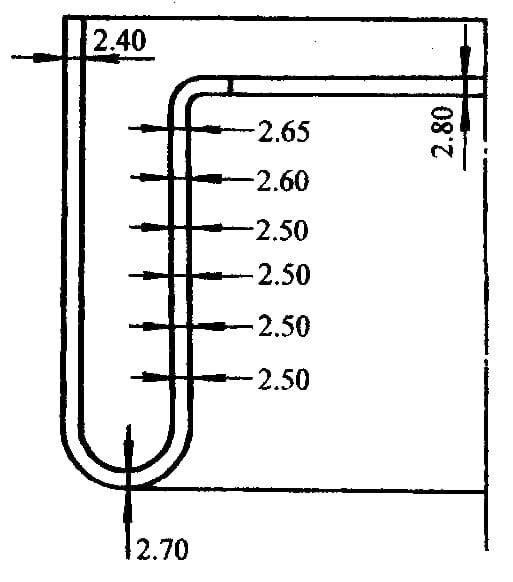
5) De dikte van de binnenwand is ongeveer gelijk aan de dikte van de buitenwand en alleen de rand onder belasting is iets dikker (Afbeelding 6-38).
De experimentele condities van het onderdeel in Figuur 6-38 zijn als volgt:
De buis is gemaakt van laag koolstofstaal, Duit = 90 mm, t0= 2,4 mm, H =150 mm.
De diameter van de holle matrijs (Figuur 6-37d) is Dd = 97 mm.
De diameter van de bolle matrijs (Figuur 6-37d) is Dp =72mm.
6) Door de afwezigheid van wrijving en de dubbele druk van de convexe en concave matrijzen op de wand van het onderdeel, heeft het onderdeel een hoge maatnauwkeurigheid (Afbeelding 6-37d).
Figuur 6-37 Rolvormproces met trekspanning (verbeterd binnenwaarts vormproces)
Voorwaarden voor een succesvolle implementatie van dit proces:
FPerforatiegat≥FRolling (6-22)
De ponskracht omvat drie elementen (symbool in Figuur 6-37d): de belasting die plastische vervorming van het materiaal bij straal rp veroorzaakt; de belasting die nodig is om de wrijvingskracht tussen de ponshoek bij ra en de rand van de buis te overwinnen; de belasting die nodig is voor het buigen en omgekeerd buigen van het randmateriaal van de radiale naar de axiale positie.
In de analytische uitdrukking is σ1 vertegenwoordigt de vervormingsspanning van de binnenwand.

Rolvorming omvat twee aspecten: de belasting die nodig is om het materiaal naar verschillende posities van de radius (kromming) te rollen en de belasting die nodig is voor het buigen en omgekeerd buigen van het begin tot het einde van het vervormingsgebied.
In de analyse wordt σ0 wordt gebruikt om de vervormingsspanning van de buitenwand weer te geven, en σm wordt gebruikt om de gemiddelde plastische vervormingsspanning in het vervormingsgebied weer te geven.

Conclusie:
De methode om buismaterialen te vormen door middel van trekspanningswalsen is bewezen door experimenten. Hoewel er twee voorbereidingsfasen nodig zijn voordat het walsen begint en herkristallisatiegloeien indien nodig is, heeft het de volgende voordelen ten opzichte van traditionele walsprocessen:
1) De gerolde rand draait naar het midden van de holte, waardoor hij gemakkelijk samenwerkt met andere onderdelen, zoals kogellagerzittingen.
2) De rolbelasting wordt sterk verminderd.
3) De omvormlimiet is sterk verbeterd en producten met kleinere rolstralen kan worden verkregen.
4) Er is geen wrijving en smering is niet nodig.
5) De dikte van de binnenwand is ongeveer gelijk aan die van de buitenwand en alleen de belaste randen zijn iets dikker (Afbeelding 6-38).
De experimentele condities van de in Figuur 6-38 getoonde onderdelen zijn als volgt:
Het buismateriaal is laag koolstofstaal, Duit = 90 mm, t0 = 2,4 mm en de straal H is 150 mm.
De matrijsdiameter Dd (Figuur 6-37d) is 97 mm.
De ponsdiameter (Figuur 6-37d) is Dp =72mm.
6) Door de afwezigheid van wrijving en de dubbele druk van de stempel en matrijs op de wand van het onderdeel, heeft het onderdeel een hogere maatnauwkeurigheid (Afbeelding 6-37d).