Liefhebbers van metaalbewerking opgelet! Ben je het zat om te gissen naar de juiste tonnage voor je kantpers? Zoek dan niet verder! In deze blogpost duiken we in de wereld van de berekening van de tonnage van de afkantpers, met de expertise van een doorgewinterde werktuigbouwkundig ingenieur als leidraad. Ontdek praktische formules, handige grafieken en insidertips om de kunst van het nauwkeurig en efficiënt buigen van plaatmetaal onder de knie te krijgen. Bereid je voor op een hoger niveau van kantpersen!
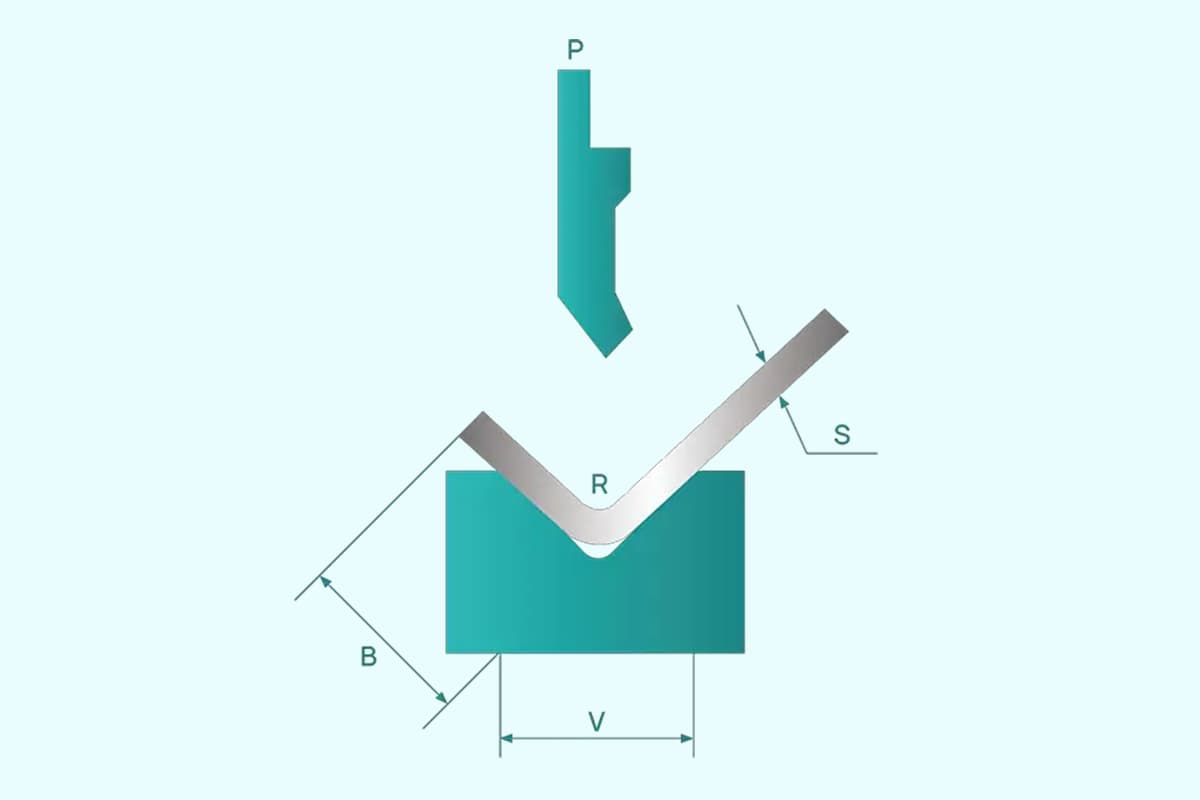
Afkantpers tonnage is de kracht die nodig is om een metalen plaat te buigen met een afkantpers. Deze kracht wordt gemeten in tonnen en is van vitaal belang voor het maken van nauwkeurige buigingen bij metaalbewerking. Een nauwkeurige berekening van de tonnage zorgt voor resultaten van hoge kwaliteit en verlengt de levensduur van de apparatuur, zodat problemen zoals schade aan het gereedschap en onnauwkeurig buigen worden voorkomen.
Verschillende materialen hebben verschillende krachten nodig vanwege hun treksterkte. Roestvrij staal heeft bijvoorbeeld meer tonnage nodig dan aluminium. De materiaaldikte heeft ook een aanzienlijke invloed op de vereiste kracht, aangezien dikkere materialen exponentieel meer kracht nodig hebben om te buigen.
De lengte van de bocht beïnvloedt de benodigde tonnage. Langere bochten vereisen meer tonnage door de grotere weerstand over de lengte van het materiaal.
De grootte van de matrijsopening beïnvloedt de vereiste kracht. Voor kleinere matrijsopeningen is een hogere tonnage nodig omdat het materiaal in een kleinere ruimte moet worden geperst, terwijl voor grotere matrijsopeningen minder kracht nodig is.
Het type gereedschap, zoals V-dies of offset gereedschap, heeft invloed op de tonnagevereisten. Zo moeten zwanenhalsgereedschappen, ontworpen om werkstukinterferentie te voorkomen, voorzichtig worden gehanteerd om overtonnaging te voorkomen.
De buigmethode - luchtbuigen, onderbuigen of coining - beïnvloedt de tonnage. Voor luchtbuigen is de minste tonnage nodig, voor onderbuigen is meer nodig en voor oprollen is de hoogste tonnage nodig.
Je kunt de volgende tonnagecalculator voor kantpersen gebruiken om de benodigde buigkracht te bepalen voor jouw buigen van plaatmetaal. De calculator biedt zowel metrische als Engelse eenheden. Persoonlijk raad ik aan om de onderstaande tonnage calculator te gebruiken, omdat dit waarschijnlijk de beste en handigste methode is om de benodigde buigkracht te berekenen.
De aanbevolen V-openingsbreedte voor de onderste matrijs
| S | 0,5-3 mm | 3-8 mm | 9-10 mm | >12 mm |
| V | 6*S | 8*S | 10*S | 12*S |
Als de plaatmetaal Het te buigen materiaal is zacht staal met een dikte van 4 mm en een buiglengte van 3,2 m. De theoretische breedte van de onderste matrijsopening moet 8 keer de dikte zijn, wat 32 mm is. Voer deze cijfers in de bovenstaande calculator in (vergeet niet dat de eenheden in mm zijn) en we krijgen een waarde van 106,12 Ton.
Dit betekent dat je een minimale buigkracht van 106 ton nodig hebt om aan je buigbehoeften te voldoen. Natuurlijk vermenigvuldigen we het eindresultaat meestal met een veiligheidsfactor van 1,1, en de resulterende waarde is de afkantpers tonnage die je kunt kiezen.
Als de verhouding breedte/dikte (V/S) niet gelijk is aan 9 en de verhouding straal/breedte niet gelijk is aan 0,16, is de bovenstaande calculator niet geldig.
Bekijk de bijgewerkte methode voor het berekenen van de buigkracht op een afkantpers.
Gebruik in plaats daarvan de volgende buigkrachtcalculator.
De grootte van de buigkracht wordt beïnvloed door factoren zoals de grootte van het werkstuk, de mechanische eigenschappen van het materiaal, de afstand tussen de scharnierpunten van de matrijs, de relatieve buigradius, de speling tussen de matrijzen, de wrijvingscoëfficiënt tussen het materiaal en de matrijs, de minimale buigkracht tussen het materiaal en de matrijs. buighoeken de buigmethode.
Daarom is het moeilijk om de buigkracht in theorie precies te berekenen.
In de praktijk worden vaak empirische formules of vereenvoudigde theoretische formules gebruikt voor de berekening.
Er zijn momenteel twee populaire formules voor het berekenen van de tonnage van de afkantpers.
De eerste formule wordt vaak gebruikt in China en de tweede in andere landen.
Echter, ongeacht welke formule wordt gebruikt, de berekende benodigde kantpersdruk is in principe hetzelfde. Hieronder zal ik deze twee formules afzonderlijk introduceren.
waar,
Bijvoorbeeld:
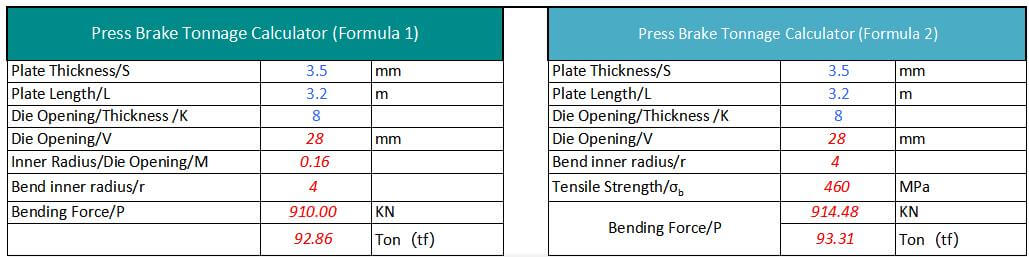
Plaatdikte S=4mm, breedte L=3m, σb=450N/mm²
In het algemeen sleufbreedte V=S*8
Daarom is P=650*4²*3/4*8=975 (KN) = 99,5 (Ton)
Het resultaat verkregen met de buigkrachtformule komt sterk overeen met de gegevens in de buigkrachtgrafiek.
Merk op dat methode #1 voor het berekenen van de tonnage van de kantpers gebaseerd is op milde stalen materiaal.
Als het materiaal roestvrij staal, aluminium of messing is, kun je de berekeningsresultaten eenvoudig aanpassen door ze te vermenigvuldigen met de coëfficiënten in de volgende tabel.
| Materiaal | Coëfficiënten |
| Zacht staal | 1 |
| Roestvrij staal | 1.6 |
| Aluminium | 0.65 |
| Messing | 0.5 |
Bijvoorbeeld:
Plaatdikte S=4mm, breedte L=3m, σb=450N/mm²
In het algemeen sleufbreedte V=S*8
Daarom is P=1,42*450*4²*3/48=958,5 (KN) = 96 (Ton)
De sleutel tot buigplaat metaal met verschillende materialen is om de treksterkte van dat specifieke materiaal te bepalen en vervolgens de vereiste buigkracht te berekenen met de bovenstaande formule.
De onderstaande tabel met treksterkte kan als referentie dienen:
| Materiaal | Zacht (N/mm²) | Hard (N/mm²) |
|---|---|---|
| Lood | 25 – 40 | – |
| Tin | 40 – 50 | – |
| Aluminium | 93 | 1710 |
| Aluminiumlegering Type 4 | 230 | 480 |
| Duraluminium | 260 | 480 |
| Zink | 150 | 250 |
| Koper | 220 – 280 | 300 – 400 |
| Messing (70:30) | 330 | 530 |
| Messing (60:40) | 380 | 490 |
| Fosfor Brons / Brons | 400 – 500 | 500 – 750 |
| Nikkel zilver | 350 – 450 | 550 – 700 |
| Koudgewalst ijzer | 320 – 380 | – |
| Staal .1% Koolstof | 320 | 400 |
| Staal .2% Koolstof | 400 | 500 |
| Staal .3% Koolstof | 450 | 600 |
| Staal .4% Koolstof | 560 | 720 |
| Staal .6% Koolstof | 720 | 900 |
| Staal .8% Koolstof | 900 | 1100 |
| Staal 1.0% Koolstof | 1000 | 1300 |
| Siliciumstaal | 550 | 650 |
| Roestvrij staal | 650 – 700 | – |
| Nikkel | 440 – 500 | 570 – 630 |
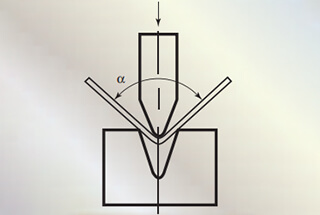
Bij luchtbuigen is de openingsbreedte V van de onderste matrijs wordt meestal gekozen als 8 tot 10 keer de dikte van de plaat, S.
Fabrikanten van afkantpersen vermelden vaak de overeenkomstige waarden van de matrijsbreedte, V, en de binnendiameter, r, van het buigwerkstuk in hun buigkrachtparametertabel.
Als algemene regel,
r=(0,16~0,17)V
Wanneer de binnenstraal echter niet gelijk is aan (0,16-0,17)V, is de bovenstaande berekeningsformule niet langer van toepassing.
In deze gevallen moet u verwijzen naar een nieuwe berekeningsmethode om de vereiste buigkracht of de tonnage van de kantpers te bepalen.
Het volgende is de calculator:
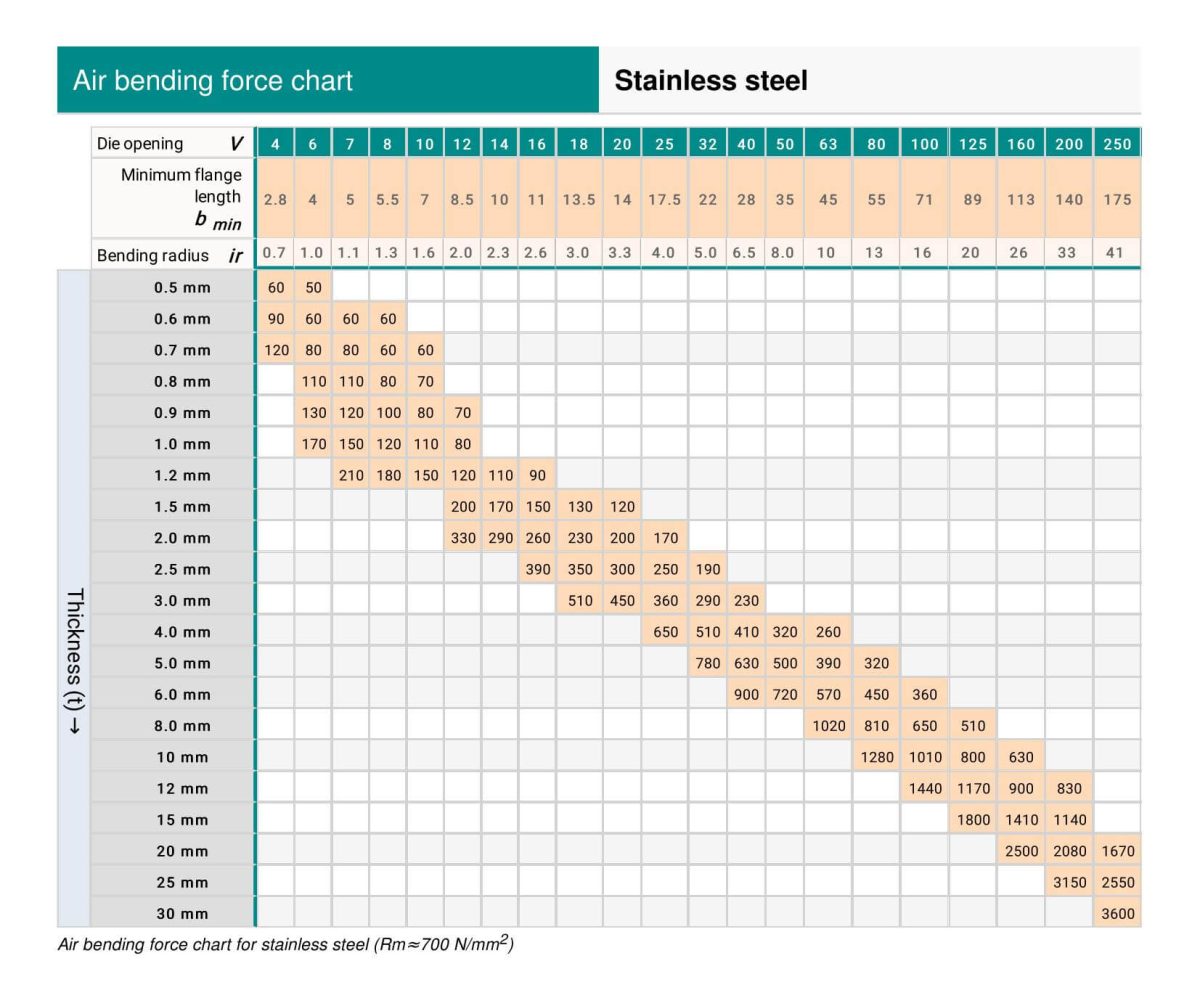
De onderstaande tonnagetabel voor kantpersen kan je helpen om de benodigde buigkracht gemakkelijk te bepalen.
Voor instructies over het lezen van een tonnagetabel van een afkantpers, zie deze post.
Zie ook:
Gegevens van V, R, B
Hoe tabellen van het aantal slagen op de afkantpers lezen?
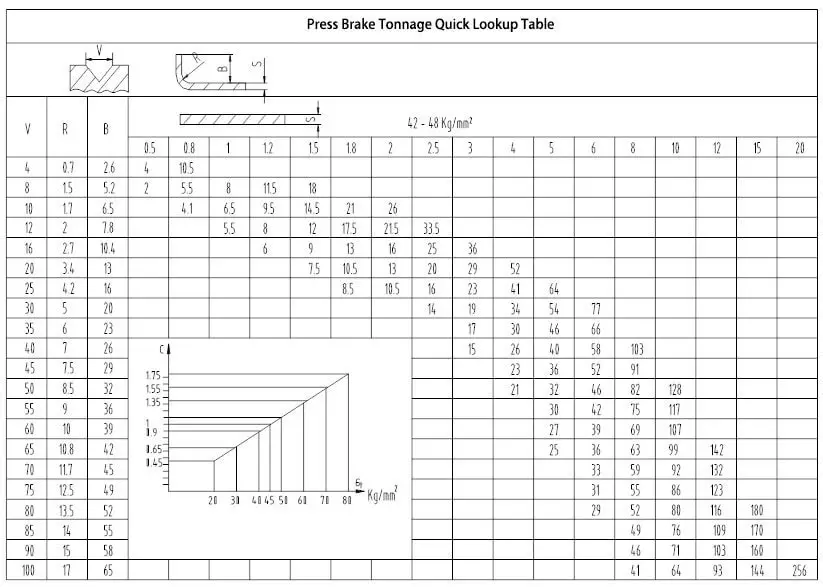
De tonnage in de tonnagetabel van de afkantpers is gebaseerd op een plaat met een treksterkte van σb=450N/mm² en een lengte van L=1m.
Nu je het buigen krachtgrafiekDe volgende stap is om te begrijpen hoe je de tonnage van de afkantpers kunt vinden in de grafiek.
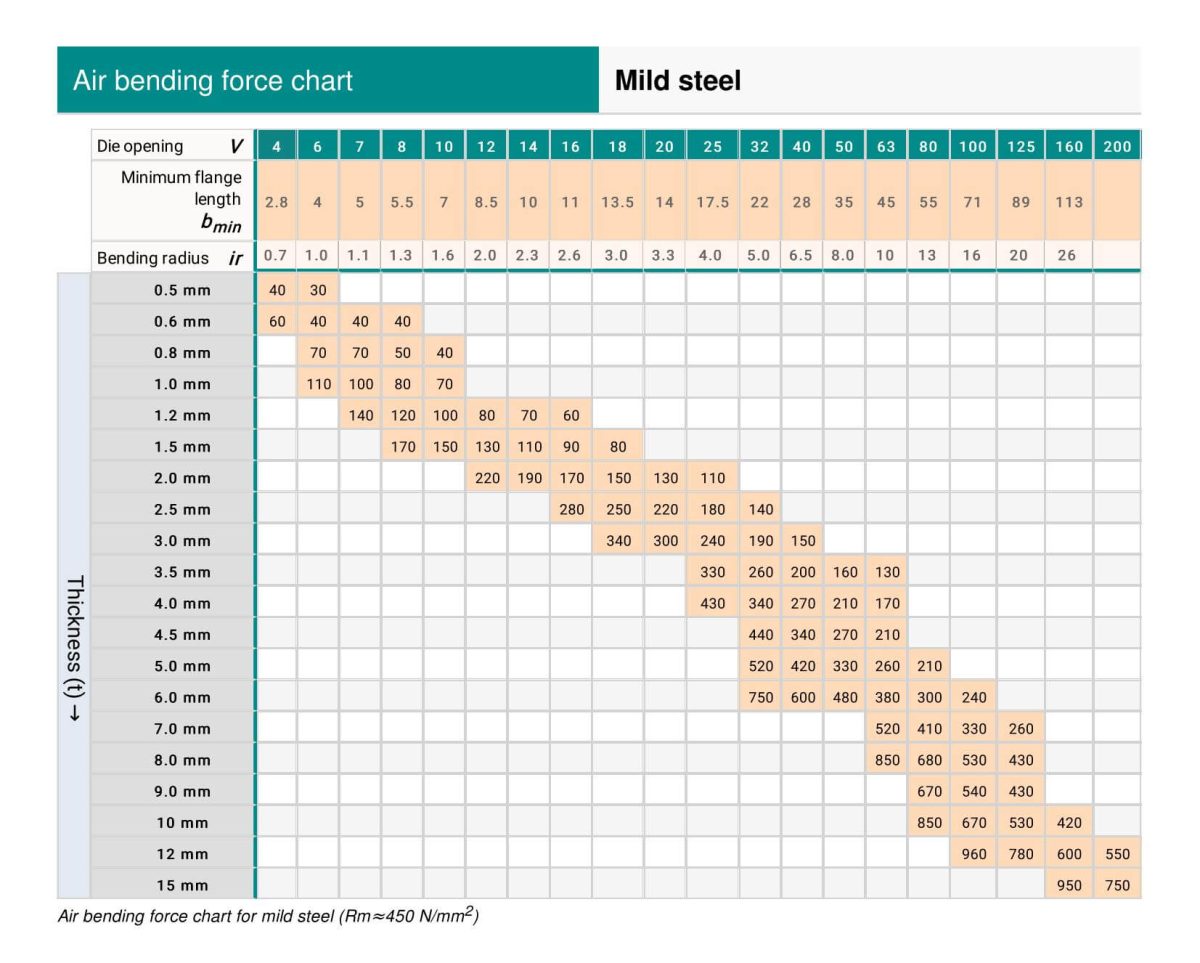
Ervan uitgaande dat je metalen plaat een dikte van 4 mm heeft, is de algemene regel dat de V-opening van de onderste matrijs 8 keer de dikte van de plaat moet zijn.
Bij dikkere platen is echter een grotere V-opening nodig.
De hieronder vermelde aanbevolen V-openingen kunnen als referentie dienen:
| S | 0,5-3 mm | 3-8 mm | 9-10 mm | >12 mm |
| V | 6*S | 8*S | 10*S | 12*S |
Laten we eens kijken naar een metalen plaat met een dikte van 4 mm.
Gewoonlijk moet de vouwopening van de onderste matrijs 8 keer de dikte van de plaat zijn. Voor dikkere platen moet de vouwopening echter groter zijn.
Om de benodigde afkantpers tonnage te bepalen, moeten we de afkantpers tonnage tabel raadplegen.
Zoek eerst de rij met een dikte van "4" en bepaal dan de bijbehorende V-openingswaarde van 32 (4 * 8).
Het snijpunt van de rij en de kolom waar de waarden "4" en "32" samenkomen, geeft een tonnage van 330 KN aan.
Als we een plaat van 4 mm moeten buigen die 3 meter lang is, dan is de benodigde tonnage 330 * 3 = 990 KN, of ongeveer 101 ton. In dit geval raden we aan om een afkantpers te kiezen met een tonnage van minstens 100 ton.
Het is echter beter om te kiezen voor een grotere tonnage, zoals 120 ton, omdat de levensduur van de machine langer zal zijn als deze langere tijd op volle belasting werkt.
Hemming is een type buiging waarvoor meer tonnage nodig is dan voor standaard luchtbuigen.
De volgende tabellen illustreren de tonnage die nodig is voor zomen en naaien.
(1) Tonnageoverzicht voor omzoomen en naaien van zacht staal
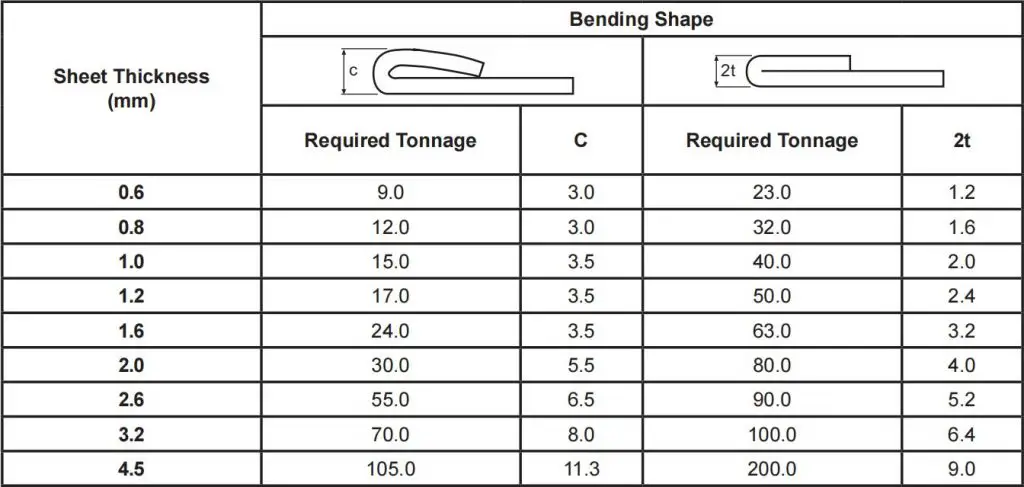
Opmerking: Vereiste tonnage wordt gegeven per lengte van 1 meter.
(2) Tonnageoverzicht voor omzoomen en stikken van roestvrij staal
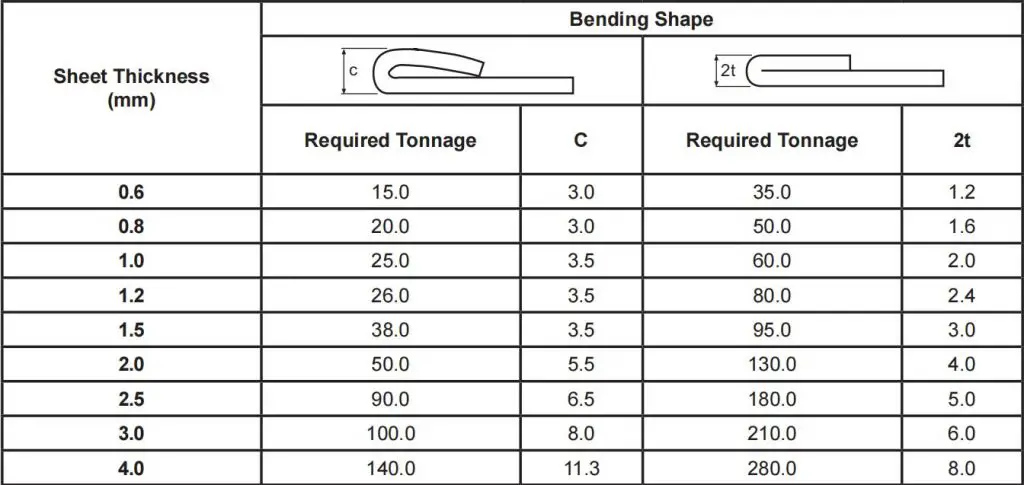
Opmerking: Vereiste tonnage wordt gegeven per lengte van 1 meter.
Tijdens het buigen van plaatmetaal is een buigradius vereist op het buigpunt, die niet te groot of te klein moet zijn, maar op de juiste manier moet worden gekozen. Als de buigradius te klein is, kan er gemakkelijk scheurvorming ontstaan op het buigpunt, terwijl bij een te grote buigradius de buiging kan terugveren.
De optimale buigradius (binnenste buigradius) voor verschillende materialen van verschillende diktes wordt weergegeven in de onderstaande tabel.
Minimale buigradiuswaarde (mm)
| Materiaalwetenschap | Gloeien staat | Koudvervormen | ||
| Overeenkomende positie tussen de richting van de buigcurve en de vezelrichting | ||||
| verticaal | parallel | verticaal | parallel | |
| 08, 10 | 0.1t | 0.4t | 0.4t | 0.8t |
| 15, 20 | 0.1t | 0.5t | 0.5t | 1.0t |
| 25, 30 | 0.2t | 0.6t | 0.6t | 1.2t |
| 4550 | 0.5t | 1.0t | 1.0t | 1.7t |
| 65Mn | 1.0t | 2.0t | 2.0t | 3.0t |
| Aluminium | 0.1t | 0.35t | 0.5t | 1.0t |
| Koper | 0.1t | 0.35t | 1.0t | 2.0t |
| Zacht messing | 0.1t | 0.35t | 0.35t | 0.8t |
| Half hard messing | 0.1t | 0.35t | 0.5t | 1.2t |
| Fosforbrons | / | / | 1.0t | 3.0t |
De gegevens in de bovenstaande tabel zijn optimaal en dienen alleen ter referentie. In feite is de afronding van het buigblad van de fabrikant meestal 0,3, met een paar buigbladen met een afronding van 0,5.
Voor gewone platen van laag koolstofstaal, roestvast aluminiumplaten, messing platen, koperen platen, enz. is een binnenafronding van 0,2 over het algemeen voldoende. Voor sommige hoog koolstofstaal, hard aluminium en super hard aluminium, kan dit type buigafronding leiden tot buigbreuken of barsten van de buitenste afronding.
Plaatmetalen buigonderdelen hebben een buigradius r nodig bij de bocht. Meestal hebben de blauwdrukken voor plaatwerkonderdelen duidelijke markeringen voor de buigradius. De uiteindelijke maat na het buigen wordt bepaald door de buigradius r0 en de hoeveelheid springrug △r, dus,
r = r0 + △r.
In de werkelijke productie ligt de gebruikte ponsradius r0 meestal tussen 0,3 en 0,5 mm, wat als een constante kan worden beschouwd en een kleine invloed heeft op de buigradius. Dit betekent dat de buigradius r nauw samenhangt met de terugvering △r.
De grootte van de terugvering is echter gerelateerd aan de buigdruk, die op zijn beurt wordt bepaald door de matrijssleufbreedte B en de plaatdikte t. Een toename van de matrijssleufbreedte B vermindert de buigdruk en vergroot de terugvering, terwijl een afname van B de buigdruk doet toenemen en de terugvering vermindert.
Daarom zijn, onder bepaalde omstandigheden van de buigmachine, de factoren die de buigradius het meest beïnvloeden de stempelradius r, de matrijssleufbreedte B en de plaatdikte t.
De volgende formule kan worden gebruikt om de afkantpers te berekenen buigradius:
De minimale binnenrand is de kortste zijde die gebogen kan worden zonder dat het plaatmetaal tijdens het buigen in de vouw glijdt.
In feite moet het plaatmetaal aan beide zijden van de vezel liggen terwijl de vereiste hoek wordt bereikt, anders zal het in de vezel glijden met als gevolg onbevredigende resultaten.
De minimale interne rand kan worden berekend met de volgende formule:
Als de vereiste hoek 90° is, minimale interne rand = V x 0,67
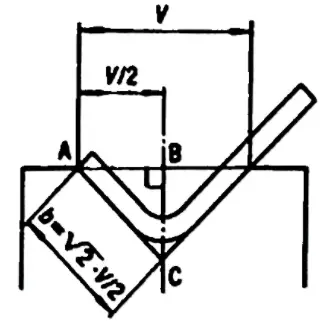
Deze formule is afgeleid van een meetkundige berekening, omdat de minimale interne rand de diagonaal is van een vierkant met zijde=V/2. Door vervolgens de straal in aanmerking te nemen, wordt het resultaat benaderd tot V x 0,67.
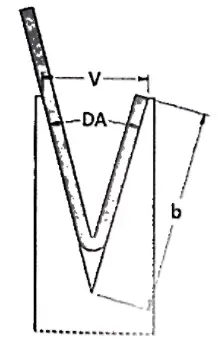
Als de vereiste hoek anders is dan 90°, zal de minimale binnenrand ook anders zijn, omdat de kortste zijde die op de vouw kan liggen afhankelijk is van de hoek.
Sterker nog, als een profiel een scherpe hoek heeft, wordt het plaatmetaal verder in de dieve geduwd en moet de zijkant langer zijn.
Aan de andere kant, als een profiel een stompe hoek heeft, heeft het een kortere zijde nodig om op een matrijs te liggen. Daarom moeten correctiefactoren worden gebruikt om de juiste minimale binnenrand te berekenen.
| Hoek | Correctiefactoren |
| 30° | B = (V x 0,67) x 1,6 |
| 60° | B = (V x 0,67) x 1,1 |
| 90° | B = (V x0,67) x 1,0 |
| 120° | B = (V x 0,67) x 0,9 |
| 150° | B = (Vx 0,67) x 0,7 |
De berekeningsformule voor de minimale buighoek is verschillend voor verschillende buighoeken, die je in de onderstaande tabel kunt vinden.
| 165° | 135° | 120° | 90° | 60° | 45° | 30° |
| 0.51×V | 0.55×V | 0.58×V | 0.71×V | 1×V | 1.31×V | 1.94×V |
L-buigen
Referentietabel voor binnenste buigstraal R en minimale buighoogte van koudgewalst dun staal staalplaat materialen:
| Serienummer | Materiaaldikte | Breedte van holle groef | Punch R | Minimale buighoogte |
| 1 | 0.5 | 4 | 0.2 | 3 |
| 2 | 0.6 | 4 | 0.2 | 3.2 |
| 3 | 0.8 | 5 | 0.8/0.2 | 3.7 |
| 4 | 1.0 | 6 | 1/0.2 | 4.4 |
| 5 | 1.2 | 8 (of 6) | 1/0.2 | 5.5/4.5 |
| 6 | 1.5 | 10 (of 8) | 1/0.2 | 6.8/5.8 |
| 7 | 2.0 | 12 | 1.5/0.5 | 8.3 |
| 8 | 2.5 | 16（14） | 1.5/0.5 | 10.7/9.7 |
| 9 | 3.0 | 18 | 2/0.5 | 12.1 |
| 10 | 3.5 | 20 | 2 | 13.5 |
| 11 | 4.0 | 25 | 3 | 16.5 |
Z-buigen
De minimale buigmaat L voor Z-buigen van plaatmetaal met verschillende diktes wordt weergegeven in de onderstaande tabel:
Minimumhoogte van z-bocht:
| Serienummer | Materiaaldikte | Breedte van holle groef | Punch R | Z-bocht hoogte L |
| 1 | 0.5 | 4 | 0.2 | 8.5 |
| 2 | 0.6 | 4 | 0.2 | 8.8 |
| 3 | 0.8 | 5 | 0.8/0.2 | 9.5 |
| 4 | 1.0 | 6 | 1/0.2 | 10.4 |
| 5 | 1.2 | 8（6） | 1/0.2 | 11.7（10.7） |
| 6 | 1.5 | 10（8） | 1/0.2 | 13.3（12.3） |
| 7 | 2.0 | 12 | 1.5/0.5 | 14.3 |
| 8 | 2.5 | 16（14） | 1.5/0.5 | 18.2（17.2） |
| 9 | 3.0 | 18 | 2/0.5 | 20.1 |
| 10 | 3.5 | 20 | 2 | 22 |
| 11 | 4.0 | 25 | 3 | 25.5 |
Hoek terugvering buigen:
Δα = b - a
waar:
b - Werkelijke hoek van het werkstuk na de terugkaatsing
a - hoek van de matrijs
Grootte van de reboundhoek:
De terugveringshoeken voor 90° enkelvoudige luchtbuigingen staan in de tabel hieronder.
| Materiaal | r/t | Dikte t (mm) | ||
| <0.8 | 0.8~2 | >2 | ||
| Laag koolstofstaal | <1 | 4° | 2° | 0° |
| Messing, σb=350MPa | 1~5 | 5° | 3° | 1° |
| Aluminium, zink | >5 | 6° | 4° | 2° |
| Middelgroot koolstofstaal, σb=400-500MPa | <1 | 5° | 2° | 0° |
| Hard messing, σb=350-400MPa | 1~5 | 6° | 3° | 1° |
| Hard koper, σb=350-400MPa | >5 | 8° | 5° | 3° |
| Hoog koolstofstaal, σb＞550Mpa | <1 | 7° | 4° | 2° |
| 1~5 | 9° | 5° | 3° | |
| >5 | 12° | 7° | 6° | |
Factoren die rebound beïnvloeden en maatregelen om rebound te verminderen:
Het type materiaal dat gebogen wordt is cruciaal bij het bepalen van de benodigde tonnage. Verschillende materialen hebben verschillende treksterktes, wat een directe invloed heeft op de kracht die nodig is om te buigen. Zo heeft zacht staal een treksterkte van ongeveer 400 MPa, terwijl roestvrij staal ongeveer 600 MPa of meer kan bereiken. Dit verschil betekent dat er meer kracht nodig is om roestvast staal te buigen dan zacht staal. Daarnaast speelt de dikte van het materiaal een belangrijke rol; dikkere materialen vragen exponentieel meer kracht om de gewenste buiging te krijgen. Een plaat roestvrij staal van 10 mm dik zal aanzienlijk meer tonnage vereisen dan een plaat van 2 mm dik.
De materiaaldikte is recht evenredig met de benodigde tonnage. Dikkere materialen hebben meer kracht nodig om te buigen. Deze relatie is niet lineair, maar exponentieel; een verdubbeling van de materiaaldikte verdubbelt de benodigde tonnage meer dan. Als een plaat van 5 mm dik bijvoorbeeld 50 ton kracht vereist, dan kan een plaat van 10 mm dik meer dan 100 ton vereisen. Daarom is het nauwkeurig meten en verantwoorden van de materiaaldikte essentieel bij het berekenen van de tonnage.
De grootte van de matrijsopening, of V-die, is een kritieke factor voor de benodigde tonnage. Kleinere matrijsopeningen vereisen een hogere tonnage, omdat het materiaal in een nauwere ruimte moet worden geperst, waardoor de weerstand toeneemt. Voor een matrijsopening van 30 graden is bijvoorbeeld minder kracht nodig dan voor een matrijsopening van 10 graden voor hetzelfde materiaal en dezelfde dikte. Omgekeerd vereisen grotere matrijsopeningen minder kracht, waardoor het buigproces eenvoudiger wordt.
Verschillende buigmethodes vereisen verschillende krachtniveaus. Luchtbuigen, onderbuigen en coining zijn de drie belangrijkste methodes die worden gebruikt bij kantpersen. Bij luchtbuigen wordt het materiaal in een V-vorm geperst, maar niet volledig. Bij deze methode is enige terugvering mogelijk, waarmee rekening moet worden gehouden in de uiteindelijke hoek. Bij onderbuigen, waarbij het materiaal helemaal naar de bodem van de matrijs wordt gedrukt, is meer kracht nodig vanwege de grotere weerstand van het materiaal. Bij het coinen, de meest krachtsintensieve methode, wordt het materiaal volledig in de matrijs gedrukt, waardoor nauwkeurige buigingen met minimale terugvering mogelijk zijn. De unieke impact van elke methode op het materiaal bepaalt de benodigde tonnage.
Het type en de staat van het gereedschap dat gebruikt wordt bij het afkantpersen is ook van invloed op de berekening van de tonnage. Verschillende soorten matrijzen en stempels hebben verschillende krachtvereisten. Zo moeten zwanenhalsgereedschappen, die ontworpen zijn om interferentie met het werkstuk te voorkomen, voorzichtig worden gehanteerd om overmatige tonnaging te voorkomen, wat kan leiden tot schade aan de apparatuur. Goed onderhouden gereedschap zorgt voor nauwkeuriger en efficiënter buigen, terwijl versleten of beschadigd gereedschap de benodigde kracht kan verhogen en de kwaliteit van de buiging in gevaar kan brengen.
Het is cruciaal om rekening te houden met de capaciteit van de afkantpers zelf. Het berekende tonnage mag niet hoger zijn dan de nominale capaciteit van de machine, omdat overbelasting kan leiden tot schade aan de apparatuur, zoals vervorming van het bed of de ram. Door ervoor te zorgen dat de afkantpers binnen zijn capaciteit werkt, wordt niet alleen schade voorkomen, maar wordt ook de levensduur van de machine verlengd. Als een afkantpers bijvoorbeeld een nominale capaciteit heeft van 100 ton, is het essentieel om de benodigde tonnage voor elke taak zorgvuldig te berekenen om te voorkomen dat deze limiet wordt overschreden.
Omgevingsfactoren, zoals temperatuur en vochtigheid, kunnen de materiaaleigenschappen beïnvloeden en dus ook de benodigde tonnage. Materialen kunnen bijvoorbeeld brosser worden bij koudere temperaturen, waardoor ze anders moeten worden gehanteerd en de kracht moet worden aangepast. Daarnaast kan vochtigheid van invloed zijn op bepaalde materialen, zoals aluminium, dat vocht kan absorberen en de eigenschappen kan veranderen. Rekening houden met deze factoren zorgt voor nauwkeurigere en betrouwbaardere buigbewerkingen.
Als oprichter van MachineMFG heb ik meer dan tien jaar van mijn carrière gewijd aan de metaalbewerkingsindustrie. Door mijn uitgebreide ervaring ben ik een expert geworden op het gebied van plaatbewerking, verspaning, werktuigbouwkunde en gereedschapsmachines voor metalen. Ik denk, lees en schrijf voortdurend over deze onderwerpen en streef er voortdurend naar om voorop te blijven lopen in mijn vakgebied. Laat mijn kennis en expertise een aanwinst zijn voor uw bedrijf.
NL 
EN 
AR 
DE 
ES 
FR 
IT 
JA 
PT 
PT_BR 
RU 
KO