Heb je je ooit afgevraagd waarom sommige materialen gemakkelijk buigen terwijl andere stijf blijven? Deze blog duikt in de fascinerende wereld van elasticiteitsmodulus en stijfheid en ontrafelt hun cruciale rol in engineering. Aan het eind zult u begrijpen hoe deze eigenschappen de sterkte en flexibiliteit van alledaagse materialen beïnvloeden.
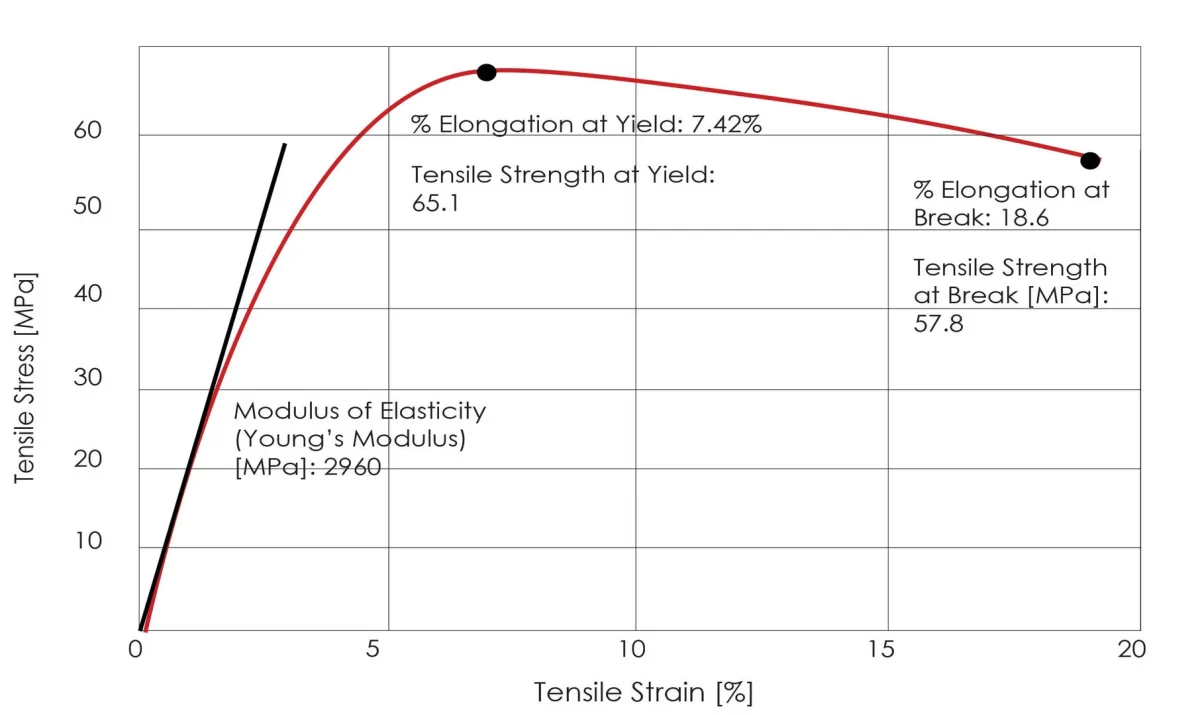
Elasticiteitsmodulus: De verhouding tussen de normale spanning en de overeenkomstige normale rek in de elastische vervormingsfase van een materiaal.
In de fase van elastische vervorming zijn spanning en rek van een materiaal evenredig, in overeenstemming met de Wet van Hooke, en de evenredigheidscoëfficiënt wordt de elasticiteitsmodulus genoemd.
De term "elasticiteitsmodulus" is een algemene beschrijving van de elasticiteit van een materiaal. Het omvat verschillende specifieke moduli, waaronder de elasticiteitsmodulus, afschuifmodulus en bulkmodulus.
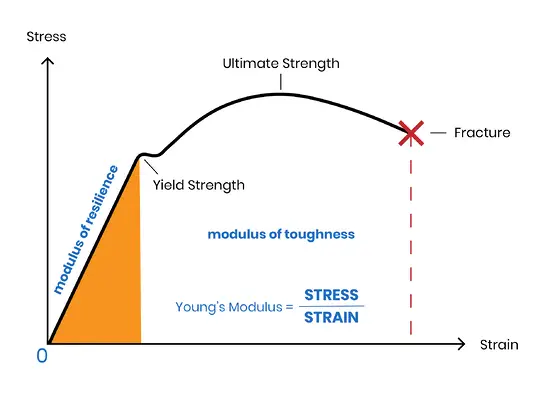
Daarom zijn "elasticiteitsmodulus" en "bulkmodulus" inclusieve termen.
Wanneer een externe kracht (bekend als "spanning") wordt uitgeoefend op een elastomeer, verandert de vorm (bekend als "rek"). De elasticiteitsmodulus wordt gedefinieerd als de verhouding tussen spanning en rek.
Bijvoorbeeld:
Lineaire spanning:
Wanneer een trekkracht F wordt uitgeoefend op een dunne staaf, wordt de lineaire spanning berekend als de trekkracht gedeeld door de dwarsdoorsnede S van de staaf.
De lineaire rek wordt berekend als de rek van de staaf (dL) gedeeld door de oorspronkelijke lengte (L).
De lineaire spanning gedeeld door de lineaire rek is gelijk aan de elasticiteitsmodulus, E = (F / S) / (dL / L).
Schuifspanning:
Wanneer een zijwaartse kracht (meestal een wrijvingskracht) f wordt uitgeoefend op een elastomeer, verandert deze van een vierkante in een ruitvorm.
Deze vervormingshoek staat bekend als de "afschuifspanning" en de bijbehorende kracht gedeeld door het spanningsgebied wordt "afschuifspanning" genoemd.
De schuifspanning gedeeld door de schuifrek is gelijk aan de schuifmodulus, G = (f / S) / a.
Volume Spanning:
Wanneer een totale druk P wordt uitgeoefend op het elastomeer, wordt dit "volumespanning" genoemd.
De volumevermindering van het elastomeer (-dV) gedeeld door het oorspronkelijke volume (V) wordt "volumerek" genoemd.
De volumespanning gedeeld door de volumevervorming is gelijk aan de bulkmodulus, K = P / (-dV / V).
In het algemeen, als er geen verwarring bestaat, verwijst de elasticiteitsmodulus van metalen naar de elasticiteitsmodulus van Young, ook bekend als de positieve elasticiteitsmodulus.
Eenheid: E (elasticiteitsmodulus) wordt gemeten in GPa.
De elastische modulus is een cruciale prestatieparameter van technische materialen.
Vanuit een macroperspectief meet het het vermogen van een object om elastische vervorming te weerstaan, terwijl het vanuit een microperspectief de bindingssterkte tussen atomen, ionen of moleculen weergeeft.
Factoren die de bindingssterkte beïnvloeden, kunnen ook de elasticiteitsmodulus van een materiaal beïnvloeden, zoals bindingswijze, kristalstructuur, chemische samenstelling, microstructuur, temperatuur en andere factoren.
De elasticiteitsmodulus van metalen materialen kan meer dan 5% fluctueren door verschillende legeringssamenstellingen, warmtebehandelingen en koude plastische vervormingen.
In het algemeen is de elasticiteitsmodulus van metalen materialen is een index voor mechanische eigenschappen die ongevoelig is voor structuur.
Legeren, warmtebehandeling (vezelstructuur) en koude plastische vervorming hebben een beperkt effect op de elasticiteitsmodulus en externe factoren zoals temperatuur en belastingssnelheid hebben er een verwaarloosbaar effect op.
Daarom wordt de elasticiteitsmodulus in algemene technische toepassingen als een constante beschouwd.
Eenheid: GPa (gigapascal) voor elasticiteitsmodulus.
De elasticiteitsmodulus is een maat voor de weerstand van een materiaal tegen elastische vervorming.
Hoe hoger de waarde, hoe groter de spanning die nodig is om een bepaalde hoeveelheid elastische vervorming te veroorzaken, wat betekent dat het materiaal stijver is en minder elastische vervorming ondervindt bij een gegeven spanning.
De elasticiteitsmodulus, weergegeven door E, is een maat voor de hoeveelheid spanning die een materiaal nodig heeft om elastische vervorming per eenheid te ondergaan onder een externe kracht.
Het vertegenwoordigt het vermogen van het materiaal om elastische vervorming te weerstaan en kan worden vergeleken met de stijfheid van een bron.
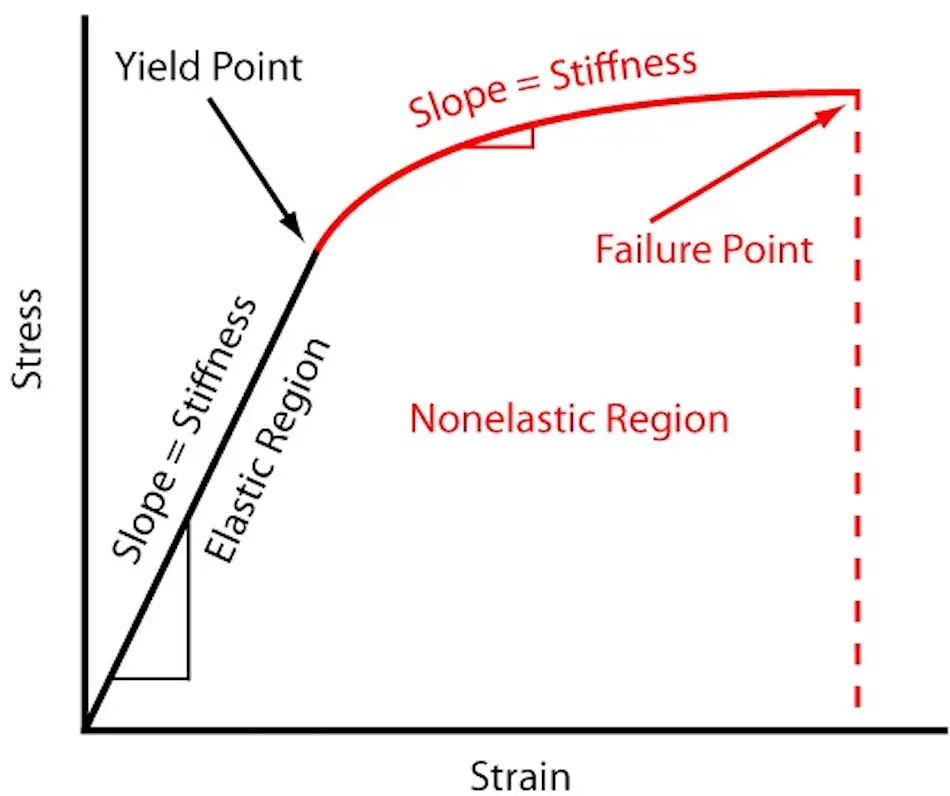
Stijfheid" verwijst naar het vermogen van een constructie of onderdeel om elastische vervorming te weerstaan. Het wordt bepaald door de kracht of het moment dat nodig is om een eenheid van rek te produceren.
De rotatiestijfheid wordt weergegeven door "k" en kan worden berekend als "k = M / θ", waarbij "M" het toegepaste koppel is en "θ" de rotatiehoek.
Andere stijfheden zijn:
De methode om stijfheid te berekenen kan worden onderverdeeld in twee benaderingen: de kleine-verplaatsingstheorie en de grote-verplaatsingstheorie.
De grote verplaatsingstheorie houdt rekening met de vervorming van de constructie na belasting en vormt dienovereenkomstig de evenwichtsvergelijking, wat nauwkeurige resultaten oplevert, maar met een complexer berekeningsproces.
De kleine verplaatsingstheorie daarentegen gaat ervan uit dat de constructie niet significant vervormd is, zodat de interne kracht kan worden verkregen uit de externe belasting en vervolgens kan worden gebruikt om de vervorming te berekenen.
Deze benadering wordt veel gebruikt in de meeste mechanische ontwerptoepassingen, omdat ze veel eenvoudiger op te lossen is.
In de berekening van buigvervorming van balken wordt bijvoorbeeld vaak de kleine verplaatsingstheorie gebruikt omdat de werkelijke vervorming erg klein is.
Deze theorie houdt in dat de eerste afgeleide van de doorbuiging in de krommingsformule wordt genegeerd en dat de tweede afgeleide van de doorbuiging wordt gebruikt om de kromming van de balkas te benaderen, wat het oplossingsproces helpt vereenvoudigen door de differentiaalvergelijking te lineariseren.
Wanneer meerdere belastingen tegelijkertijd optreden, kan de buigvervorming die door elke belasting wordt veroorzaakt afzonderlijk worden berekend en vervolgens gecombineerd.
De weerstand tegen vervorming onder een statische belasting staat bekend als statische stijfheid, terwijl de weerstand tegen vervorming onder een dynamische belasting dynamische stijfheid wordt genoemd, wat de hoeveelheid dynamische kracht betekent die nodig is voor een amplitude per eenheid.
Als de storende kracht langzaam verandert (d.w.z. de frequentie van de storende kracht is veel lager dan de natuurlijke frequentie van de constructie), is de dynamische stijfheid in wezen gelijk aan de statische stijfheid.
Als de storende kracht echter snel verandert (d.w.z. de frequentie van de storende kracht is veel groter dan de natuurlijke frequentie van de constructie), zal de structurele vervorming relatief klein zijn en dus zal de dynamische stijfheid relatief groot zijn.
Als de frequentie van de storende kracht dicht bij de natuurlijke frequentie van de constructie ligt, treedt resonantie op en zal de dynamische stijfheid minimaal zijn, waardoor de constructie het gemakkelijkst vervormt en de dynamische vervorming meerdere keren of zelfs meer dan tien keer die van de vervorming door statische belasting kan bereiken.
Overmatige vervorming van onderdelen kan invloed hebben op hun werking.
Zo kan overmatige vervorming van een tandwielas invloed hebben op het in elkaar grijpen van tandwielen en overmatige vervorming van een machinegereedschap kan de bewerkingsnauwkeurigheid verminderen.
De factoren die de stijfheid beïnvloeden zijn onder andere de elasticiteitsmodulus van materialen en de structurele vorm. Het veranderen van de constructievorm kan een aanzienlijke invloed hebben op de stijfheid.
De berekening van de stijfheid vormt de basis van de trillingsleer en de stabiliteitsanalyse van constructies. Wanneer de massa constant blijft, resulteert een hoge stijfheid in een hoge eigenfrequentie.
De spanningsverdeling in een statisch onbepaalde constructie is gerelateerd aan de stijfheidsverhouding van elk onderdeel.
In breukmechanica analyse kan de spanningsintensiteitsfactor van een gescheurd lid worden bepaald op basis van zijn flexibiliteit.
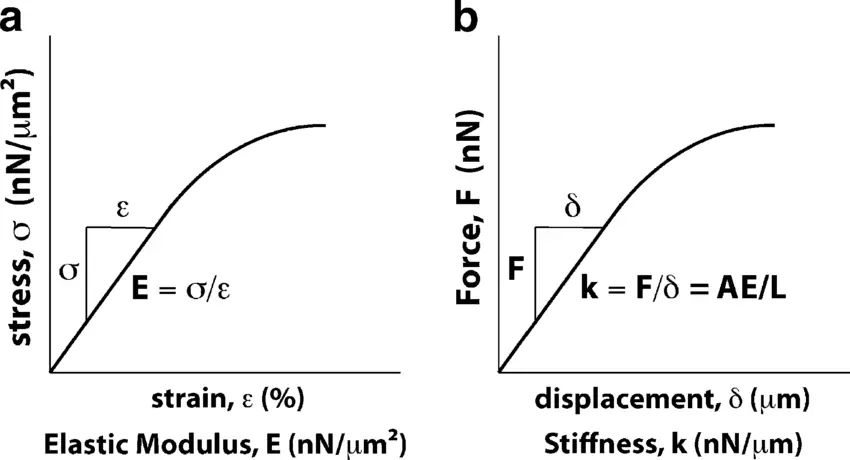
Stijfheid en elasticiteitsmodulus zijn fundamentele concepten in de materiaalkunde, die elk verschillende aspecten van de weerstand van een materiaal tegen vervorming beschrijven. Hoewel ze verwant zijn, spelen ze een verschillende rol in de analyse en toepassing van materialen.
Elastische modulus, ook bekend als Young's modulus, is een specifieke maat voor het inherente vermogen van een materiaal om vervorming onder spanning te weerstaan. Het kwantificeert de relatie tussen spanning (kracht per oppervlakte-eenheid) en rek (proportionele vervorming) in het lineair elastische gebied van de spanning-rek curve van het materiaal. De elasticiteitsmodulus is een materiaaleigenschap en is onafhankelijk van de vorm of grootte van het materiaal. Hij wordt uitgedrukt in drukeenheden, zoals Pascal (Pa).
Stijfheid daarentegen is een bredere term die verwijst naar de weerstand van een constructie tegen elastische vervorming onder een toegepaste belasting. Het is niet alleen een materiaaleigenschap, maar hangt ook af van de geometrie en de randvoorwaarden van de constructie. Stijfheid wordt meestal uitgedrukt als de kracht die nodig is om een verplaatsingseenheid te bereiken (bijv. Newton per meter, N/m).
De stijfheid van een constructie-element kan worden afgeleid uit de elasticiteitsmodulus van het materiaal en de geometrie van het element. Bijvoorbeeld, de buigstijfheid (EI) van een balk is het product van de elasticiteitsmodulus (E) en het traagheidsmoment (I) van de doorsnede van de balk. Op dezelfde manier is torsiestijfheid (GI) het product van de afschuifmodulus (G) en het polaire traagheidsmoment (I).
Stijfheid is cruciaal bij technisch ontwerp, vooral voor componenten die hun vorm moeten behouden onder belasting, zoals spindels, geleiderails en draadspillen. Het is ook essentieel voor constructies die een strikte controle op vervorming vereisen, zoals vliegtuigvleugels en assemblages met hoge precisie.
Sterkte is het vermogen van een materiaal om permanente vervorming en breuk te weerstaan onder externe krachten. Het omvat verschillende soorten sterkte, waaronder vloeigrens, treksterkte, druksterkte en buigsterkte. Deze eigenschappen zijn cruciaal voor het bepalen van de belastbaarheid en duurzaamheid van mechanische onderdelen.
Het begrijpen van het onderscheid tussen stijfheid en elasticiteitsmodulus is essentieel voor het ontwerpen en analyseren van mechanische componenten en constructies. Terwijl de elasticiteitsmodulus een maat is voor de intrinsieke weerstand van een materiaal tegen vervorming, houdt stijfheid rekening met zowel materiaaleigenschappen als geometrische factoren om de algehele weerstand van een constructie tegen vervorming te beschrijven. Beide concepten zijn essentieel om de prestaties en betrouwbaarheid van technische ontwerpen te garanderen.
Als oprichter van MachineMFG heb ik meer dan tien jaar van mijn carrière gewijd aan de metaalbewerkingsindustrie. Door mijn uitgebreide ervaring ben ik een expert geworden op het gebied van plaatbewerking, verspaning, werktuigbouwkunde en gereedschapsmachines voor metalen. Ik denk, lees en schrijf voortdurend over deze onderwerpen en streef er voortdurend naar om voorop te blijven lopen in mijn vakgebied. Laat mijn kennis en expertise een aanwinst zijn voor uw bedrijf.
NL 
EN 
AR 
DE 
ES 
FR 
IT 
JA 
PT 
PT_BR 
RU 
KO