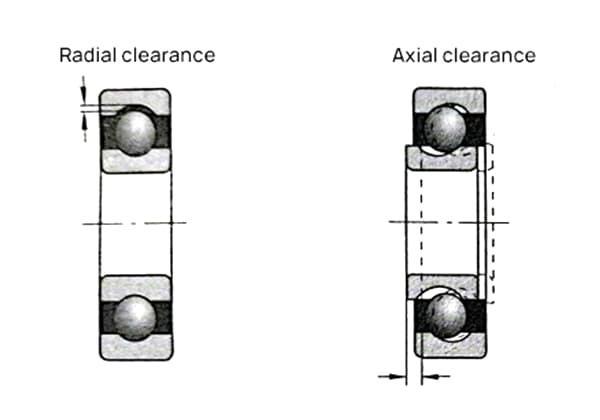
Heb je je ooit afgevraagd wat een perfecte cirkel is? In de wereld van werktuigbouwkunde is rondheid een cruciaal concept dat de prestaties en levensduur van roterende componenten beïnvloedt. Dit artikel duikt in de fijne kneepjes van rondheid en onderzoekt de definitie, meetmethoden en factoren die de rondheid beïnvloeden. Of je nu een doorgewinterde ingenieur of een nieuwsgierige leerling bent, het begrijpen van rondheid is essentieel voor het ontwerpen en onderhouden van machines met hoge precisie.
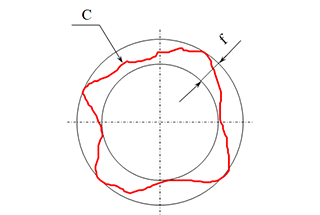
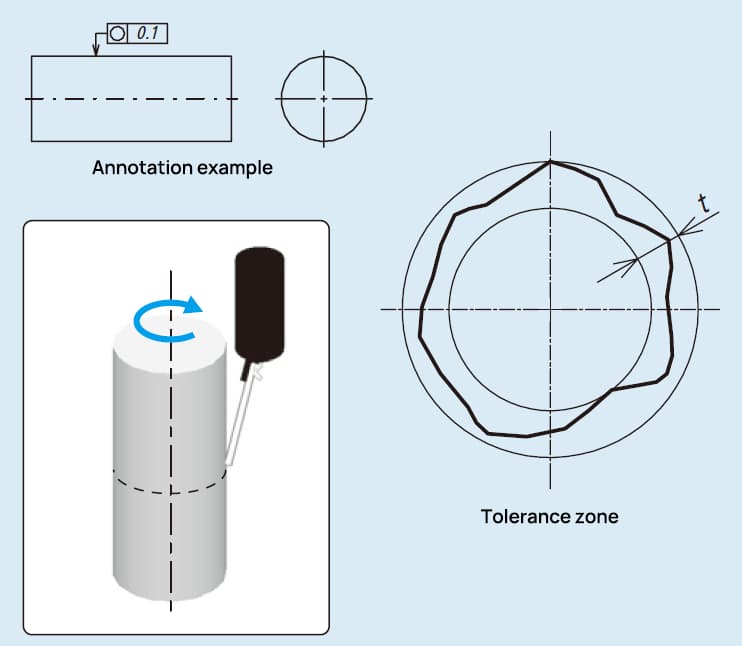
In de Japanse industriële norm (JIS) B0621-1984, die betrekking heeft op de definitie en uitdrukking van vorm- en positieafwijkingen, wordt rondheid gedefinieerd als "de afwijking van de geometrische cirkel van een cirkelvormig lichaam". Deze standaard biedt een nauwkeurige methode om rondheid weer te geven, wat cruciaal is om de kwaliteit en functionaliteit van ronde componenten in de machinebouw te garanderen.
De weergave van rondheid in JIS B0621-1984 is als volgt:
Voor roterende componenten is het evalueren van hun werkelijke ronde vorm cruciaal om een goede werking en een lange levensduur te garanderen. De onmiddellijke zorg is het bepalen van de rondheidstolerantie, dat is de toegestane afwijking van een perfecte cirkel. Deze evaluatie begint met:
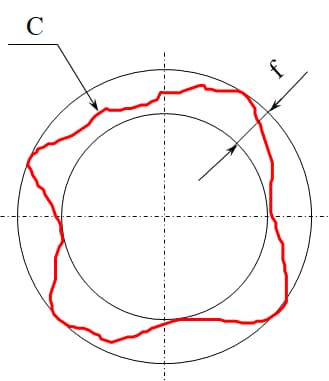
Rondheidstolerantie, ook wel rondheidstolerantie genoemd, is een specificatie voor geometrische dimensionering en tolerantie (GD&T) die de toegestane afwijking van een perfecte cirkel in een dwarsdoorsnedevlak van een cilindrisch of sferisch onderdeel definieert. Het zorgt ervoor dat de gemeten omtrek van een onderdeel binnen een gespecificeerde tolerantiezone ligt, die het gebied is tussen twee concentrische cirkels van dezelfde doorsnede met een straalverschil van t. Deze tolerantiezone garandeert dat het onderdeel een consistente cirkelvorm behoudt binnen de gedefinieerde grenzen.
Stel je een doorsnede voor van een cilindrisch onderdeel. De tolerantiezone voor rondheid wordt weergegeven als het gebied tussen twee concentrische cirkels. Het straalverschil t tussen deze cirkels vertegenwoordigt de toegestane afwijking van de ideale cirkelvorm. Elk punt op de werkelijke omtrek van het onderdeel moet binnen deze zone vallen om aan de eisen voor rondheidstolerantie te voldoen.
Verschillende factoren kunnen leiden tot afwijkingen in rondheid en cilindriciteit, die de precisie en functionaliteit van bewerkte onderdelen beïnvloeden. Dit zijn de meest voorkomende oorzaken:
Er zijn verschillende methoden om rondheid te evalueren, elk met zijn eigen unieke eigenschappen en voordelen. De te gebruiken methode wordt meestal gekozen op basis van de specifieke vereisten van het werkstuk.
Zoals:
Diameter methode
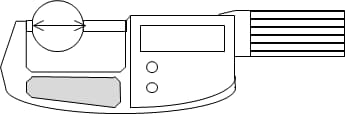
De rondheid kan direct gemeten worden met gereedschap zoals micrometers. Deze methode is eenvoudig en gemakkelijk uit te voeren. Bij het evalueren van driehoekige en vijfhoekige cirkels met gelijke diameter is het echter gemakkelijk om ze als rond te meten als ze dat niet zijn, wat leidt tot onjuiste resultaten.
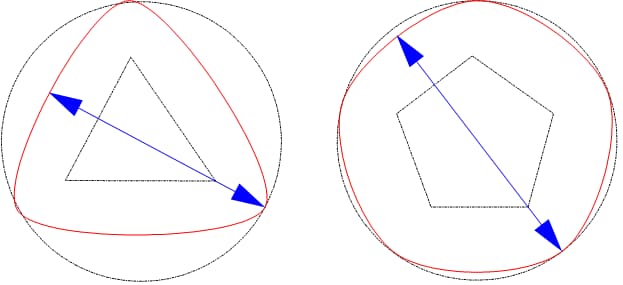
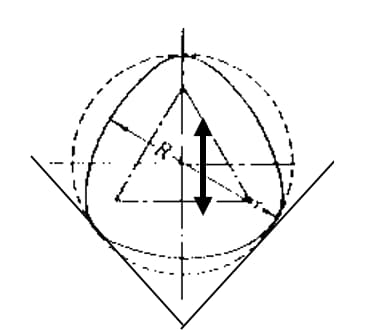
Driepuntsmethode
De driepuntsmethode kan rondheidsgegevens verkrijgen via [V-blok + micrometer / meter + bank].
De driepuntsmethode kan echter resulteren in onjuiste metingen door verschillen in de raaklijn op het geselecteerde steunpunt en moeilijkheden bij het bepalen van het middelpunt van het referentiepunt. Bovendien kunnen er tijdens de meting fouten optreden door de op- en neerwaartse beweging met de rotatie van het te meten object.
Zoals:
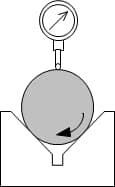
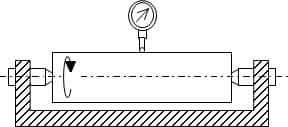
Straalmethode
De radiusmethode evalueert de rondheid aan de hand van het verschil tussen de maximale en minimale radius die verkregen wordt nadat het werkstuk één cyclus is gedraaid. Zoals in de afbeelding te zien is, kunnen de meetresultaten ook gemakkelijk beïnvloed worden door de horizontale beweging van het werkstuk.
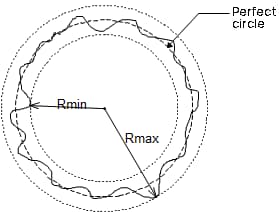
De tolerantiezone ligt tussen twee concentrische cirkels op dezelfde sectie
Centrale methode
Vergeleken met de centrale methode wordt de radiusmethode meestal gebruikt voor nauwkeuriger metingen. De gegevens van de rondheidsdetectie zijn afhankelijk van de referentiecirkel. Verschillende evaluatiemethoden van de testcirkel resulteren in verschillende centrale posities van de referentiecirkel, waardoor de axiale positie van de gemeten cirkelvorm wordt beïnvloed.
Om de rondheid te bepalen, wordt de gemeten contour in een cirkel gepast en wordt de som van de kwadraten van de afwijking van de contourgegevens ten opzichte van de cirkel geminimaliseerd. Vervolgens wordt de rondheidswaarde gedefinieerd als het verschil tussen de maximale afwijking (de hoogste piekwaarde tot de laagste dalwaarde) van de contour en de cirkel.
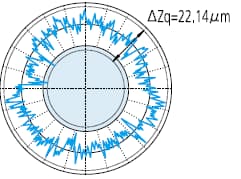
ΔZｑ=Rmax-Rmin, symbool dat rondheidswaarde door LSC weergeeft
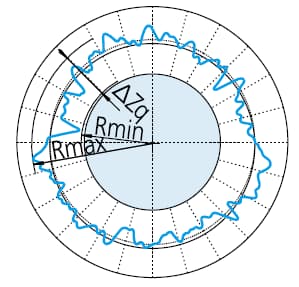
Om het radiale verschil te minimaliseren, worden twee concentrische cirkels rond de gemeten contour geplaatst. De rondheidswaarde wordt gedefinieerd als het radiale interval tussen de twee cirkels.
ΔZｚ=Rmax-Rmin , symbool dat rondheidswaarde door MZC weergeeft
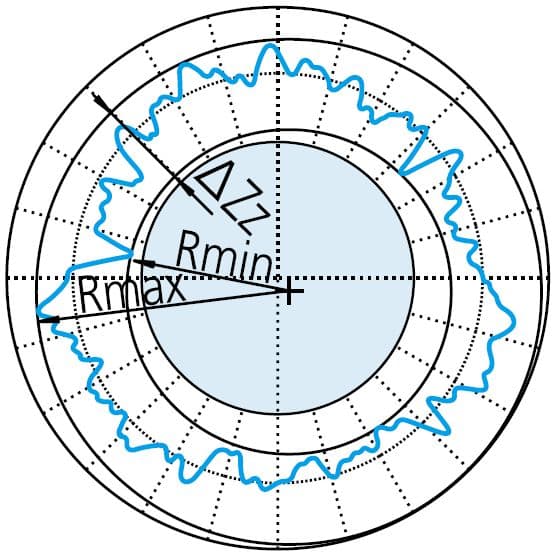
Maak eerst de kleinste cirkel die het gemeten profiel omsluit. Vervolgens wordt de rondheidswaarde gedefinieerd als de maximale afwijking tussen de contour en de cirkel. Deze methode wordt vaak gebruikt voor het evalueren van assen, staven en soortgelijke objecten.
ΔZｃ=Rmax-Rmin , het symbool van de rondheidswaarde door MCC.
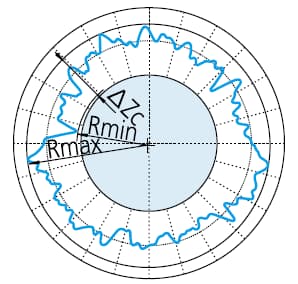
Maak de grootste cirkel die het gemeten profiel kan omsluiten. Vervolgens wordt de rondheidswaarde gedefinieerd als de maximale afwijking tussen de contour en de cirkel.
ΔZｉ=Rmax-Rmin , het symbool dat de afrondingswaarde aangeeft via MIC.
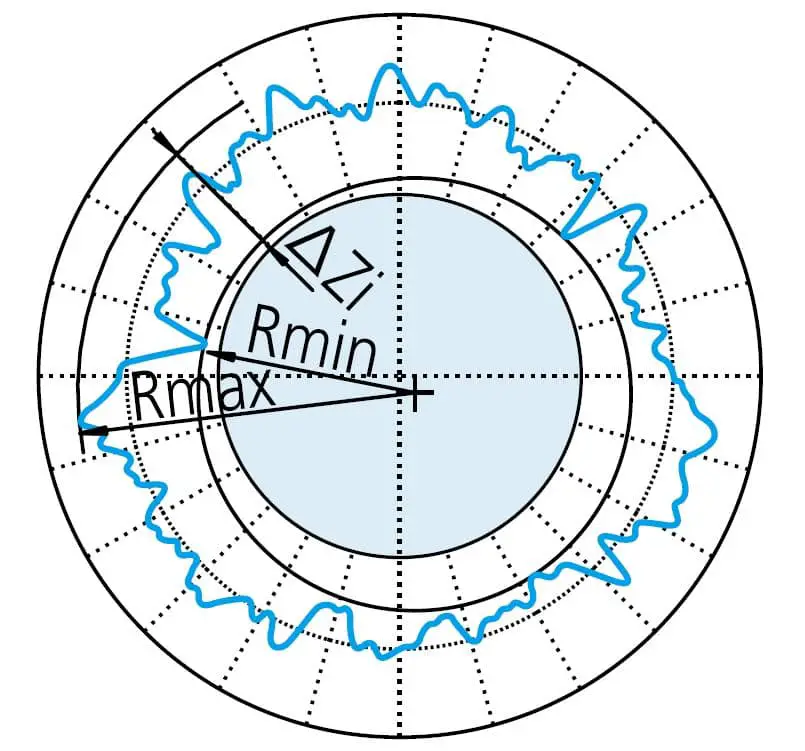
Bij het evalueren van rondheid wordt de verkregen contour meestal gefilterd om de invloed van onnodige ruis te verminderen of te elimineren.
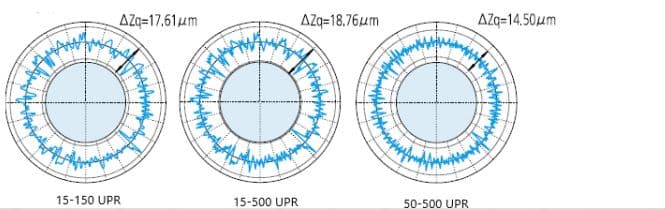
Filtermethoden en de ingestelde filtergrenswaarden (UPR: fluctuaties per omwenteling) kunnen variëren afhankelijk van de specifieke meetvereisten. De onderstaande afbeelding illustreert de verschillende effecten van filterinstellingen op de gemeten contour.
Geen filter:
Laagdoorlaatfilter:
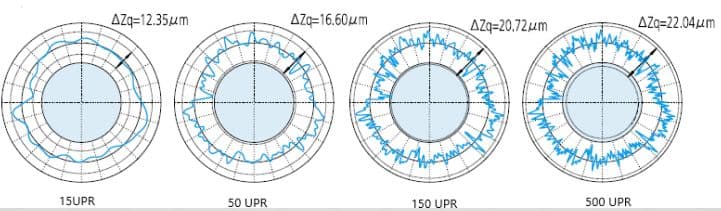
Banddoorlaatfilter:
Wat kunnen deze cijfers ons als beoordelaars vertellen?
Afbeelding: grafiek van meetresultaten
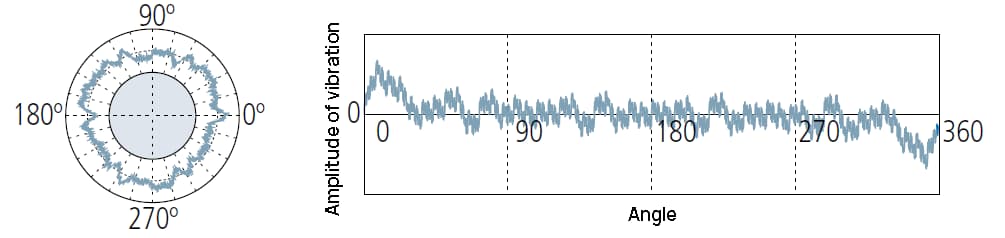
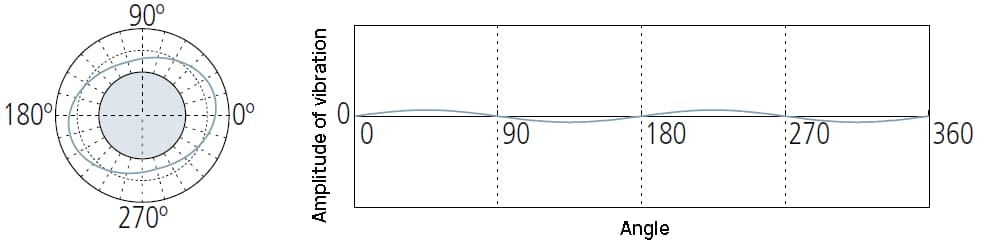
1 UPR: slechts één golf wordt behouden na filteren:
1UPR-component geeft de excentriciteit van het werkstuk ten opzichte van de roterende as van het meetinstrument aan.
De amplitude van de golfvorm hangt af van de aanpassing van het niveau.
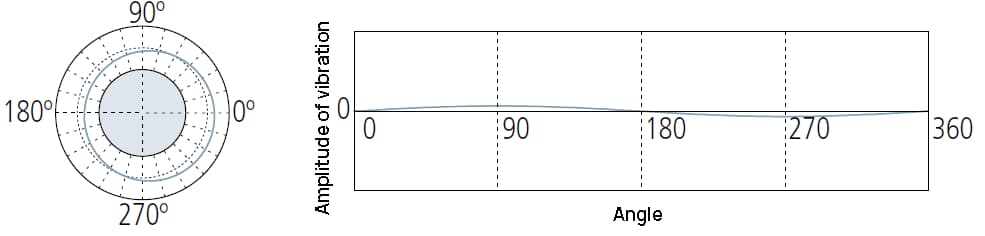
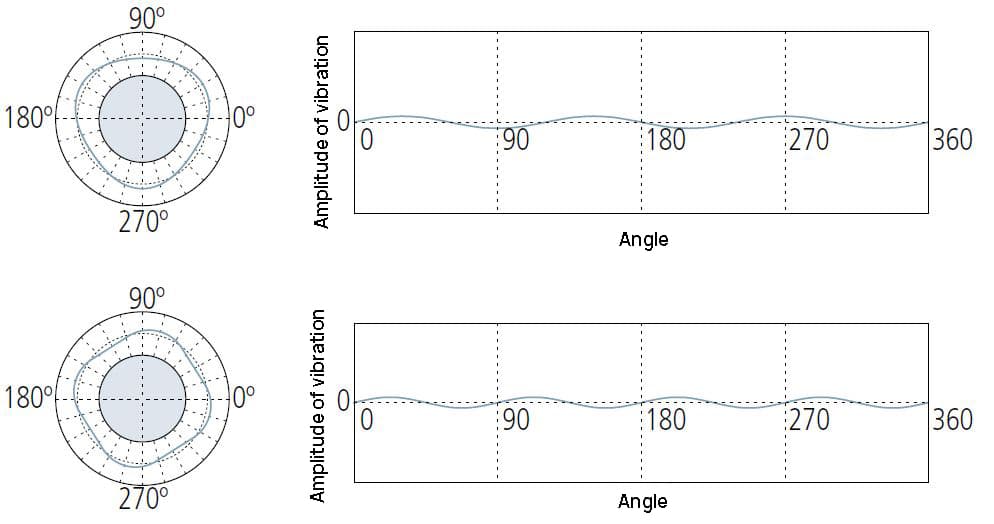
2UPR componenten kunnen aangeven:
① Onvoldoende niveau-instelling van meetinstrumenten;
② Rondloop veroorzaakt door onjuiste installatie van het werkstuk op de machine die de vorm vormt;
③ De vorm van het werkstuk is ovaal, bijvoorbeeld in de zuiger van een IC-motor.
Kan aangeven:
① Vervorming veroorzaakt door te strakke borgklem op het meetinstrument.
② Ontspanningsvervorming veroorzaakt door het loslaten van spanning bij het ontladen uit de vaste klauwplaat van de bewerkingsmachine.
Het verwijst meestal naar onevenwichtige factoren in de verwerkingsmethode of het productieproces van werkstukken.
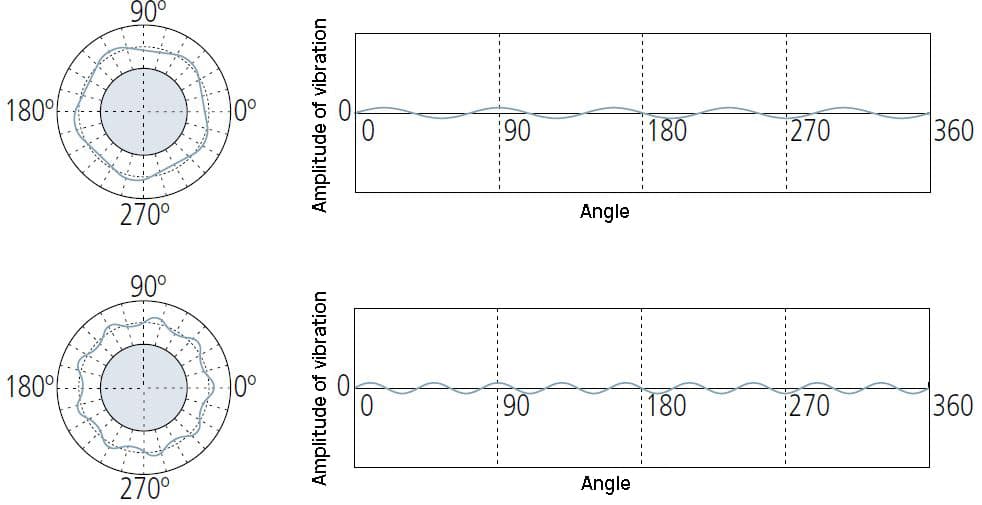
15 (of meer) UPR-condities hebben meestal hun eigen oorzaak, zoals gereedschapschommelingen, machinetrilling, koelmiddeloverdrachtseffect, materiaal inhomogeniteit, enzovoort.
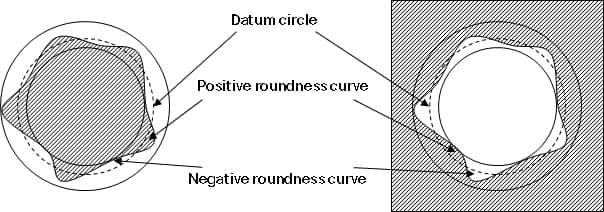
| Parameter | Betekenis |
| RONt | De gemeten waarde van rondheid vertegenwoordigt het verschil tussen de maximumwaarde van de positieve rondheidscurve en de minimumwaarde van de negatieve rondheidscurve of de som van de absolute waarden. |
| RONp | De gemeten piekhoogte van de rondheidscurve vertegenwoordigt de maximumwaarde van de positieve rondheidscurve. |
| RONV | De gemeten waarde van rondheid vertegenwoordigt de absolute waarde van de minimumwaarde van de negatieve rondheidscurve. |
| RONq | De dubbelwortelgemiddelde kwadratische rondheidsmeting vertegenwoordigt het dubbelwortelgemiddelde kwadraat van de rondheidscurve. |
Laten we tot slot eens kijken naar welke hulpmiddelen en instrumenten beschikbaar zijn om rondheid te meten?
Micrometer:
Rondheidsmeetinstrument:
Coördinatenmeetmachine:
De ruimte is beperkt en je bent welkom om een bericht achter te laten en kritiek te geven op de zaken die niet aan bod zijn gekomen.
Na het lezen van dit artikel hoop ik dat je een beter begrip hebt gekregen van rondheid. Als je nog vragen hebt, laat dan gerust een reactie hieronder achter.
Als oprichter van MachineMFG heb ik meer dan tien jaar van mijn carrière gewijd aan de metaalbewerkingsindustrie. Door mijn uitgebreide ervaring ben ik een expert geworden op het gebied van plaatbewerking, verspaning, werktuigbouwkunde en gereedschapsmachines voor metalen. Ik denk, lees en schrijf voortdurend over deze onderwerpen en streef er voortdurend naar om voorop te blijven lopen in mijn vakgebied. Laat mijn kennis en expertise een aanwinst zijn voor uw bedrijf.
NL 
EN 
AR 
DE 
ES 
FR 
ID 
IT 
JA 
PT 
PT_BR 
RU 
KO 
TR