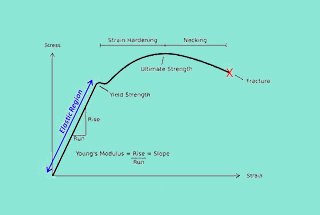
Heb je je ooit afgevraagd waarom transmissieassen meestal cirkelvormig zijn? Dit artikel gaat in op de mechanische redenen achter deze vorm en legt uit hoe een cirkelvormige dwarsdoorsnede torsieprestaties optimaliseert en stress minimaliseert. Je komt meer te weten over de voordelen van dit ontwerp om vervorming tegen te gaan en een efficiënte krachtoverbrenging te garanderen. Aan het eind begrijp je waarom het cirkelvormige ontwerp cruciaal is voor het behoud van mechanische integriteit onder wisselende belastingen. Lees verder om de engineeringprincipes te ontdekken die van de cirkelvormige transmissieas de voorkeurskeuze in mechanische systemen maken.
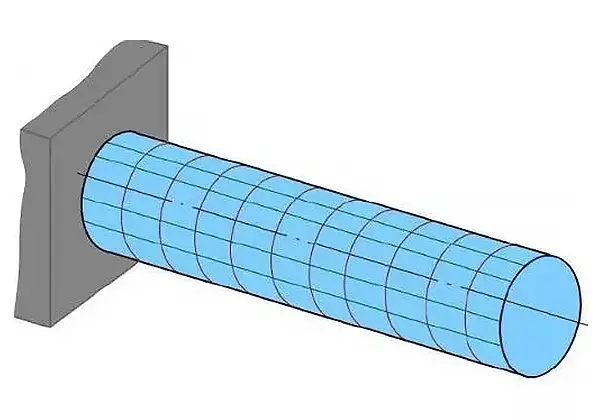
(1) Conventie voor koppelsymbolen
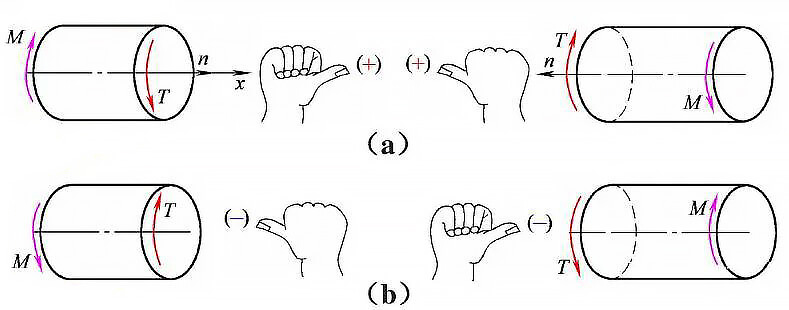
Fig. 1 richting en symbool van koppel
(2) Torsievervorming van staaf met cirkelvormige doorsnede
Na het verdraaien van een as met cirkelvormige doorsnede blijven de vorm en grootte van de doorsnede hetzelfde en blijft deze vlak. De straal van de doorsnede blijft de as waaromheen de doorsnede is gedraaid en elke doorsnede draait slechts een kleine hoek γ ten opzichte van elkaar.
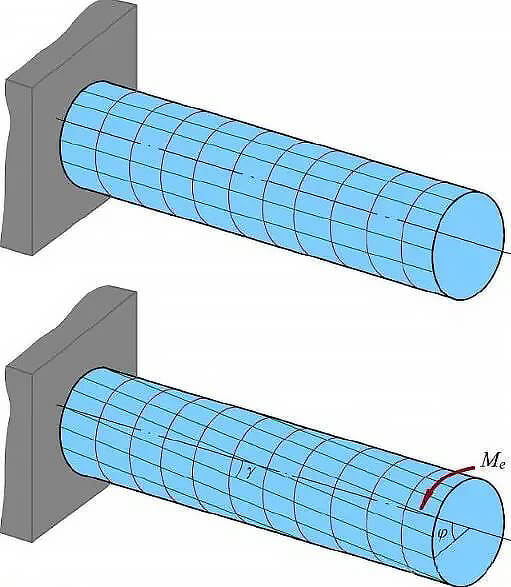
Fig. 2 torsievervorming van staaf met cirkelvormige doorsnede
(3) Torsie van staaf met niet-ronde doorsnede
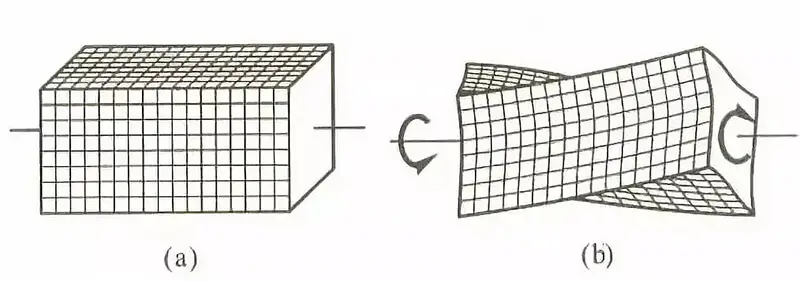
Fig. 3 torsievervorming van vierkante staaf
Vrije torsie:
Als een staaf een niet-cirkelvormige dwarsdoorsnede heeft, zal deze kromtrekken tijdens torsievervorming. De mate van kromtrekken van aangrenzende doorsneden zal hetzelfde zijn, wat betekent dat de lengte van alle longitudinale vezels in de staaf niet zal veranderen. In dit scenario zal er geen normaalspanning op de doorsnede staan, alleen afschuifspanning.
Om vrije torsie te bereiken, moeten de twee uiteinden van de rechte staaf worden onderworpen aan een extern koppel en mag de kromming van aangrenzende secties niet extern worden beperkt.
Beperkte torsie:
Wanneer een niet-uniforme rechte staaf wordt verdraaid, verandert de hoeveelheid uitgeoefende torsie over de lengte van de staaf. Als één uiteinde van de staaf gefixeerd is en niet kan bewegen, zal de mate van kromtrekken van aangrenzende delen van de staaf verschillend zijn. Naast schuifspanning zal er ook normaalspanning optreden op de dwarsdoorsnede van de staaf.
Normaal gesproken is de normaalspanning veroorzaakt door ingehouden torsie in een massieve staaf klein en kan verwaarloosd worden. Bij dunwandige staven is deze normaalspanning echter vaak te groot om genegeerd te worden.
(1) Vlakke hypothese
Na verdraaiing blijft de cirkelvormige doorsnede vlak en blijven vorm, grootte en straal ongewijzigd. De doorsneden roteren ten opzichte van elkaar met slechts een kleine hoek γ. Deze aanname geldt echter alleen voor de as van de cirkelvormige doorsnede en niet voor de as van niet-cirkelvormige doorsneden.
De afstand tussen aangrenzende secties blijft hetzelfde, behalve wanneer τzx = τzy, wat aangeeft dat er geen normaalspanning is.
σ x= σ y= σ z= τ xy=0.
Het elasticiteitsmodel wordt getoond in Fig. 4.

Fig. 4 Torsie-elastisch mechanisch model van rechte staaf
(2) Manalogie met embrane
Prandtl wees erop dat de doorbuiging van een dunne vloeistoffilm, ook bekend als een membraan, onder uniforme druk wiskundig vergelijkbaar is met de spanningsfunctie in het torsieprobleem van een rechte staaf met een gelijke doorsnede.
Het vergelijken van de torsiestang met het membraan kan helpen bij het oplossen van het torsieprobleem.
In Figuur 5 is er een uniforme film gespannen op een horizontale grens, die dezelfde vorm en grootte heeft als de doorsnede van een torsiestang.
Wanneer er een kleine gelijkmatige druk op de folie wordt uitgeoefend, zal elk punt van de folie een kleine doorbuiging ondervinden.
Als het vlak waar de grens ligt het xy-vlak is, kan de doorbuiging worden voorgesteld door z.
Vanwege de flexibele aard van de folie wordt aangenomen dat deze niet bestand is tegen buigmomenten, torsie, schuifkracht of druk. Hij verdraagt alleen een uniforme trekkracht FT, die vergelijkbaar is met de oppervlaktespanning van een vloeibare film.
Volgens deze analyse is de schuifspanning op elk punt van de dwarsdoorsnede van de torsiestang, langs elke richting, gelijk aan de helling van de film in de verticale richting op dat punt.
Er kan worden vastgesteld dat de maximale schuifspanning op de doorsnede van de torsiestang gelijk is aan de maximale helling van het membraan. De richting van de maximale schuifspanning staat echter loodrecht op de richting van de maximale helling.
Door deze aanname te doen, is het mogelijk om de maximale schuifspanning en relatieve torsiehoek te bepalen van de rechte staaf zonder cirkelvormige doorsnede in tabel 1 hieronder.

Fig. 5 Membraananalogiemodel
(1) Massieve ronde as
Onder aannames 1 en 2 zijn de mechanische eigenschappen van kunststof materialen in zuivere afschuiving wanneer de samenstellende materialen zich binnen het elastische bereik bevinden:
τ= G γ,γ Is de afschuifspanning;
γ=φ R/L( γ is de relatieve torsiehoek van twee doorsneden op een afstand van L;
φ de hoek van het eindvlak van het torsie-einde is, R de buitenstraal van de cirkel is en L de afstand tussen twee secties).

Fig. 6 Schematisch diagram van torsie van staaf met massieve cirkelvormige doorsnede
De schuifspanning bij ρ op de cirkelvormige doorsnede is:

Onder dezelfde koppelconditie is de schuifspanning (τ) op een staaf met cirkelvormige doorsnede evenredig met de afstand tot het middelpunt van de doorsnede (ρ). Dit betekent dat hoe groter de afstand tot het middelpunt, hoe hoger de schuifspanning.
Wanneer de afstand tot het middelpunt gelijk is aan de straal (R) van de cirkelvormige doorsnede, wordt de maximale schuifspanning verkregen aan de rand.
De torsie sectiemodulus (Wp) van een cirkelvormige as kan worden uitgedrukt als IP/R, waarbij IP het polaire traagheidsmoment is. Deze waarde is alleen gerelateerd aan de geometrische afmetingen van de doorsnede en niet aan de dwarsdoorsnede.
De maximale schuifspanning (τ max) kan worden berekend als T/WP, waarbij T het toegepaste koppel is.
Voor een massieve as met een cirkelvormige doorsnede is de torsie sectiemodulus (WP) ongeveer gelijk aan 0,2 maal de kubus van de diameter (D).
De torsiehoek (φ) van een ronde staaf onder torsie is gerelateerd aan de torsiestijfheid (GIP) van de ronde doorsnede, die het vermogen van de as om vervorming te weerstaan weergeeft.
De relatieve torsiehoeken van twee doorsneden op een afstand van L kunnen worden berekend met een torsieformule.
Relatieve draaihoek:
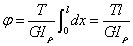
Stijfheidstoestand van ronde as:

(2) Holle ronde as
De doorsnede-torsiecoëfficiënt van holle cirkelvormige as is ongeveer: WP ≈ 0,2D3 (1- α 4),0< α= d/D<1.
Wanneer α= 0,8, is het WP 60% van de massieve cirkelvormige doorsnede, dat wil zeggen, bij hetzelfde koppel neemt de sterkte af met 40%, maar bij hetzelfde materiaal en dezelfde lengte is het gewichtsverschil 2,8 keer.
(3) Gesloten dunwandige buis
Een ronde buis met een wanddikte (a) die veel kleiner is dan de straal (R0) - meestal ≤ R0/10 - wordt een dunwandige ronde buis genoemd. Dit type pijp kan elke vorm en gelijke doorsnede hebben.
Omdat het een dunwandige pijp betreft, wordt aangenomen dat de schuifspanning gelijkmatig verdeeld is over de gehele wanddikte (t) om een benaderende oplossing te verkrijgen.
Door de reciproke schuifspanningsregel toe te passen, kan worden geconcludeerd dat het product van de gemiddelde axiale schuifspanning van alle punten op de pijpsectie en de pijpwand gelijk is, d.w.z. dat de schuifstroming (q) constant is.
Omdat de waarde van q consistent is over de hele doorsnede, is de maximale schuifspanning bij de minimale wanddikte.
Wanneer de pijpsectie cirkelvormig is, is de oppervlakte (Am) gelijk aan πR0². Het vergroten van de diameter van de cilinder kan de schuifspanning aanzienlijk verminderen.

Fig. 6 Afschuifspanningsverdeling van verschillende gangbare doorsneden
Tijdens de torsietest is de spanningsverdeling over de dwarsdoorsnede van het proefstuk ongelijkmatig. Het oppervlak ondervindt de grootste hoeveelheid spanning en naarmate we naar het midden gaan, neemt de spanning af.
Dit heeft tot gevolg dat wanneer het materiaal wordt verdraaid, de schade begint bij de buitenste laag van de ronde staaf en zich naar binnen voortplant. De scheur ontstaat vanaf de oppervlaktelaag en breidt zich naar binnen uit.
In de techniek wordt de torsietest vaak gebruikt om de oppervlaktedefecten en de prestaties van oppervlakteverharding lagen in materialen.
Zoals getoond in Fig. 7.

Fig. 7 torsietest van rond staafmonster
In het torsieproces van een ronde as gemaakt van kunststof materialen zoals koolstofstaal met een laag koolstofgehalte, zal het oppervlak van de as eerst meegeven en dan zal de omtrek worden afgesneden langs de doorsnede naarmate de torsievervorming toeneemt.
Dit is te wijten aan het feit dat de afschuifcapaciteit van het materiaal lager is dan de trekcapaciteit en dat de maximale afschuifspanning optreedt op de dwarsdoorsnede, wat leidt tot afschuiving.
Bij engineering wordt de maximale afschuifspanning op de buitenrand van de doorsnede meestal ingesteld op de afschuifgrens van het materiaal (τs) als gevaarlijke toestand en de sterkteconditie wordt op basis hiervan vastgesteld.
Maar zelfs wanneer de afschuifspanning op de rand de vloeigrens bereikt, bevinden andere onderdelen zich nog steeds in de lineaire elastische werktoestand en zal de ronde staaf geen duidelijke plastische vervorming ondergaan, waardoor het koppel kan blijven toenemen.
Rekening houdend met de plasticiteit van het materiaal, is het uiteindelijke koppel (plastisch koppel) van een massieve ronde staaf 1/3 groter dan het vloeimoment (dat het resultaat is van een vereenvoudigde technische berekening).
Wanneer de schuifspanning aan de rand van de materiaaldoorsnede de afschuifgrens van het materiaal τs bereikt, breidt het plastische gebied zich geleidelijk naar binnen uit met de toename van het torsiekoppelmoment en begint het materiaal aan de rand van de doorsnede sterker te worden.
Als het torsiekoppelmoment blijft toenemen, zal de scheur beginnen vanuit de buitenste laag van de ronde staaf en uiteindelijk afschuiven langs de dwarsdoorsnede.
Zoals getoond in Fig. 8.

Fig. 8 torsietest van rond staafmonster van kunststof
In het geval van een ronde as gemaakt van brosse materialen, zoals gietijzer, met een lagere trekcapaciteit dan afschuifcapaciteit, is de vervorming tijdens torsiefalen minimaal. De as breekt op het spiraalvormige oppervlak onder een hoek van ongeveer 45° ten opzichte van de as.
Dit komt omdat het hellende vlak onder een hoek van 135° ten opzichte van de as de maximale trekspanning ondervindt. Als de maximale trekspanning op dit gedeelte groter is dan de treksterkte van het materiaal, dan zal de as bezwijken door spanning op dit gedeelte.
Zoals getoond in Fig. 9.

Fig. 9 torsietest van monster van ronde staaf van bros materiaal
De interne torsie T die de rondhoutstaaf ondervindt, genereert niet alleen een radiale lineaire verdeling van schuifspanning op de dwarsdoorsnede, maar veroorzaakt ook een overeenkomstige schuifspanning langs het axiale vlak, wat kan leiden tot scheuren langs het axiale vlak.
Omdat hout een anisotroop materiaal is, is de schuifkracht parallel aan de vezels in de axiale richting veel kleiner dan de schuifkracht loodrecht op de vezels in de dwarsdoorsnede, wat resulteert in het scheurpatroon dat in Figuur 10 wordt weergegeven.

Fig. 10 Torsiefalen van boomstammen
De figuur illustreert de berekeningsformules voor maximale spanning en torsiehoek van vierkante, driehoekige en elliptische doorsneden, volgens de analyse van de elasticiteitstheorie.
In alle bovengenoemde gevallen treedt de maximale schuifspanning op bij de grenslijn van de doorsnede die het dichtst bij de centrale as ligt.
Voor een gesloten dunwandige pijp ervaart de positie met de dunste wanddikte ten opzichte van de centrale as de hoogste schuifspanning.

Fig. 11 berekeningsformule van torsieschuifspanning en relatieve torsiehoek van verschillende doorsneden
Laat S de oppervlakte zijn van een cirkel, vierkant, driehoek en ellips, die allemaal onderworpen worden aan hetzelfde koppel T.
De lengte van een vierkant is a = √S, terwijl de lengte van een gelijkzijdige driehoek ongeveer a ≈ 2,3√S is.
Met behulp van de berekeningsformule voor maximale spanning in de afbeelding is de maximale schuifspanning op de dwarsdoorsnede van een gelijkzijdige driehoek bij dezelfde dwarsdoorsnede en hetzelfde draaimoment ongeveer 1,8 keer zo groot als die van een vierkant.
Voor een ellips met a = b, waardoor het een cirkel is, geldt a = 0,56√S, en de maximale schuifspanning op een vierkant is ongeveer 1,32 keer die van een cirkel.
Als de ellips een ≠ b heeft, met 1 > b/a = λ > 0, dan is de verhouding van de maximale schuifspanning op de ellips tot de maximale schuifspanning op de cirkel λ√S-2. Dus hoe kleiner de waarde van λ, hoe groter de schuifspanning. Dus hoe kleiner de waarde van λ, hoe groter de schuifspanning.
Uit bovenstaande vergelijking kan worden geconcludeerd dat:
Wanneer een as dezelfde doorsnede heeft en hetzelfde koppel draagt, is de maximale schuifspanning op de cirkelvormige doorsnede het kleinst vergeleken met een niet-cirkelvormige doorsnede. Bovendien is de torsiehoek ook kleiner. Een cirkelvormige transmissieas heeft dus een natuurlijk voordeel in torsie mechanische prestaties.
Als we deze bevindingen uitbreiden naar willekeurige dwarsdoorsneden, kan worden aangetoond dat de as met cirkelvormige dwarsdoorsnede de hoogste efficiëntie heeft.
Wanneer een as dezelfde doorsnede heeft en hetzelfde koppel draagt, is de maximale schuifspanning op de cirkelvormige doorsnede het kleinst vergeleken met een niet-cirkelvormige doorsnede. Bovendien is de torsiehoek ook kleiner. Een cirkelvormige transmissieas heeft dus een natuurlijk voordeel in torsie mechanische prestaties.
Als we deze bevindingen uitbreiden naar willekeurige dwarsdoorsneden, kan worden aangetoond dat de as met cirkelvormige dwarsdoorsnede de hoogste efficiëntie heeft.
Tabel 1 formule voor koppelcontrole van asdiameter
|
Type as |
formule |
instructie |
|
massieve as |
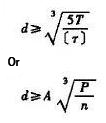 |
Waar: d - bereken de diameter van de as bij de doorsnede (mm) T-koppel overgebracht door as (N-mm) T=9550000P/n P-vermogen overgebracht door as (kW) toerental n-as (R/min) [T] - toelaatbare afschuifspanning van de as (MPa) A - coëfficiënt bepaald door [t], V-verhouding van binnendiameter d0 tot buitendiameter D van de holle cirkelvormige as |
|
holle as |
 |
De schuifspanning aan het oppervlak van een as met cirkelvormige doorsnede is hoog en het midden is relatief klein wanneer deze torsiebelasting draagt. Daarom kan het verwijderen van een deel van het materiaal dat geen volledige rol speelt in het midden, het gewicht van de as effectief verminderen en de buigweerstand verbeteren.
Maar om te beslissen of asonderdelen al dan niet hol moeten worden gemaakt, moet niet alleen rekening worden gehouden met mechanische factoren, maar ook met technologische en productiekosten. Het is belangrijk op te merken dat de wanddikte niet te dun mag zijn, anders kunnen er plaatselijke plooien ontstaan die leiden tot een verlies aan draagvermogen.
Als de wanddikte (δ) van de cilinder veel kleiner is dan de straal (R0), die meestal wordt beschouwd als ≤ R0/10, dan wordt het een dunwandige cilinder genoemd. Als de dunwandige buis echter een opening in de lengterichting van de as heeft, zal de torsieweerstand aanzienlijk afnemen. Daarom wordt meestal een membraan toegevoegd om de torsieweerstand te verbeteren. stijfheid en sterkte.
Een as bestaat meestal uit verschillende secties en spanningsconcentratie op de overgangspositie tussen deze secties is een veel voorkomende oorzaak van defecten in asonderdelen.
De literatuur kan worden geraadpleegd voor richtlijnen voor het selecteren en bepalen van de grote diameter van twee aangrenzende doorsneden en de overgangsvulling.
De cilindrische schroefveer is een veelgebruikt onderdeel in de machinebouw, gekenmerkt door zijn spiraalas en grote elastische vervorming.
In het ontwerp van een bron met een hoge belastbaarheid is sterkte meestal de eerste overweging. Voor een veer met een lage belastbaarheid is vervorming echter meestal de belangrijkste factor om rekening mee te houden.
Voor minder kritische veren kan de selectie uitsluitend worden gebaseerd op structurele afmetingen en specificaties.
Voor informatie over ontwerp- en berekeningsmethoden voor veren wordt verwezen naar relevante literatuur en de normen uit de GB/T1239-reeks, GB/T2089, DIN2089 en andere toepasselijke normen.
Onder invloed van statische belasting is er een bepaalde relatie tussen de mechanische eigenschappen van materialen in torsie en trek, dus [σ] van materialen wordt gebruikt om de toelaatbare schuifspanning[ τ]: te bepalen.
| Type materiaal | [σ] | [ τ] | [ τ] |
| kunststof | 1 | 0.5~0.7 [σ] | 0,55 of 0,577 [σ] |
| Bros materiaal | 1 | 0.7~1.0 [σ] | 0.8~1.0 [σ] |
De bovenstaande tabel laat zien dat de relatie tussen schuifspanning en normaalspanning in de literatuur verschilt.
Verschillende plastische materialen die in de literatuur worden genoemd, tonen aan dat de verhouding tussen schuifspanning en normaalspanning tussen 0,5 en 0,7 moet zijn [σ].
Deze relatie is echter een ruwe schatting en moet alleen worden gebruikt als de exacte schuifspanningsgegevens niet beschikbaar zijn.
Voor een nauwkeurige verificatie is het nodig om de specifieke torsiesterktewaarde van het materiaal te verkrijgen.