Heb je ooit moeite gehad met het nauwkeurig uitvouwen van plaatwerkonderdelen? Dit artikel verkent de kunst en wetenschap achter berekeningen voor het ontvouwen van plaatmetaal. Ontdek de belangrijkste concepten, formules en technieken die ervaren ingenieurs gebruiken om complexe geometrieën nauwkeurig uit te vouwen. Leer hoe u deze principes kunt toepassen op uw eigen ontwerpen en uw productieproces kunt stroomlijnen.
De eerste stap in het plaatbewerkingsproces is het ontvouwen van de geometrieën en het samenhangende lichaam. De nauwkeurigheid en juistheid van het ontvouwen van het monster heeft een directe invloed op de kwaliteit van het uiteindelijke onderdeel.
In het verleden gebruikten mensen, vanwege de beperkingen van de rekenhulpmiddelen, de projectiemethode om het monster te vergroten op een vlak met een verhouding van 1:1 en de werkelijke lengte van de vereiste planlijn te meten.
Deze methode is echter ingewikkeld en inefficiënt en kan niet voldoen aan de huidige productie-eisen.
Met de vooruitgang in rekenhulpmiddelen, zoals elektronische rekenmachines en het wijdverbreide gebruik van computers, plaatmetaal ontvouwen kan nu worden uitgevoerd met berekeningsmethoden.
Om de berekeningsmethode van de ontvouwingscoëfficiënt van plaatmetaal door technici te standaardiseren, maatafwijkingen van producten na het buigen te minimaliseren en zelfinspectie door werkplaatspersoneel en herkeuring door kwaliteitsinspecteurs te vergemakkelijken, is er een uniforme standaard en basis voor de ontvouwingscoëfficiënt.
Daardoor is de berekeningsnorm voor de uitklapcoëfficiënt van plaatwerk steeds meer gestandaardiseerd.
Methode voor het ontvouwen van neutrale lagen
Tijdens het buigproces ondergaat de buitenste laag trekspanning, terwijl de binnenste laag drukspanning ondervindt. De overgangslaag tussen trekspanning en drukspanning wordt de neutrale laag genoemd. De lengte van de neutrale laag tijdens het buigen blijft dezelfde als voor het buigen, waardoor het de maatstaf wordt voor het bepalen van de uitgevouwen lengte van het gebogen onderdeel.
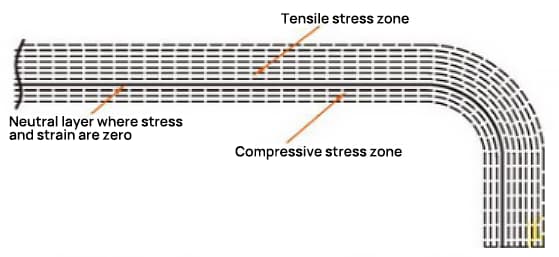
De locatie van de neutrale laag is afhankelijk van de mate van vervorming.
De positie van de neutrale laag is niet alleen gerelateerd aan de buigradius, plaatdikte, binnenwaartse verschuivingscoëfficiënt, enz., maar ook aan factoren zoals verwerkingsmethode, vorm en grootte van het plaatwerk.
Daarom kan de positie van de neutrale laag alleen bij benadering worden bepaald en in praktische toepassingen worden meestal waarden bij benadering gebruikt voor berekeningen.
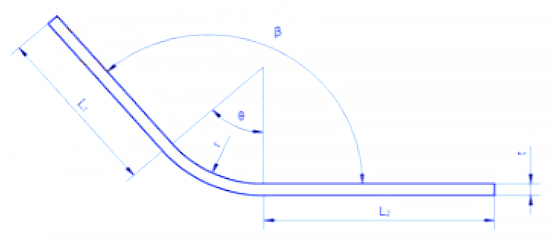
De berekeningsformule voor de lengtemaat L van de neutrale laag is:
Onder hen,
Door gebruik te maken van 3D-software voor simulaties en berekeningen van verschillende diktes, hoeken en stralen, samen met de fabricagepraktijken ter plaatse, hebben we een reeks K-factoren samengesteld. Zie Tabel 1 voor de specifieke waarden.
Tabel 1: Neutrale-laagcoëfficiënt K-waarden
| r/t | ≤05 | 0.6 | 0.8 | 1 | 1.2 | 1.3 | 1.5 | 2 | 2.5 | 3.0 | 4.0 | 5.0 | 6.0 | ≥8 |
| k | 026 | 0.28 | 0.30 | 0.32 | 0.33 | 0.34 | 0.36 | 0.38 | 0.39 | 0.4 | 0.42 | 0.44 | 0.46 | 0.5 |
Snelle ontvouwberekening voor 90°-bochten
Het uitklapdiagram voor een bocht van 90° wordt getoond in Figuur 9. De laatste jaren gebruiken we 3D-software zoals CATIA en SOLIDWORKS voor plaatwerkmodellering om de ontvouwmaten te berekenen.
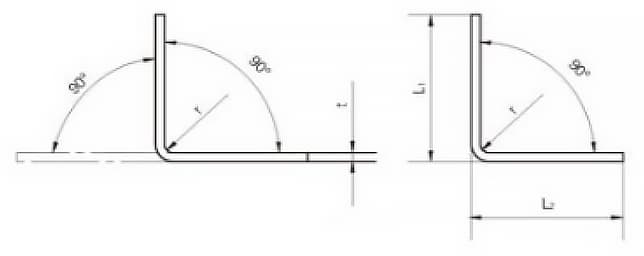
Bij herhaalde controle is gebleken dat wanneer de koude buighoek van platte staalproducten 90° is, de formule voor het berekenen van de uitgeklapte lengte L is:
L = L1 + L2 - A
Waar,
Tabel 2 90 ° buigparameters
| Dikte t/mm | Bedradingsstraal r/mm | |||||||||||
| 1 | 1.2 | 16 | 2 | 25 | 3 | 4 | 5 | 6 | 8 | 10 | 12 | |
| Compensatiewaarde A mm | ||||||||||||
| 1 | -1.92 | -1.97 | -2.10 | -2.23 | -2.41 | -2.59 | -2.97 | -3.36 | -3.79 | -4.65 | -5.51 | -6.37 |
| 1.5 | -2.90 | -3.02 | -3.18 | -3.34 | -3.70 | -4.07 | -4.45 | -5.26 | -6.11 | -6.97 | ||
| 2 | -3.84 | -3.98 | -4.13 | -4.46 | -4.81 | -5.18 | -5.94 | -6.72 | -7.58 | |||
| 2.5 | -4.80 | -4.93 | -5.24 | -5.57 | -5.93 | -6.66 | -7.42 | -8.21 | ||||
| 3 | -5.76 | 6.04 | -6.35 | -6.69 | -7.40 | -8.14 | -8.91 | |||||
| 4 | -7.7 | -7.95 | -8.26 | -8.92 | -9.62 | -10.36 | ||||||
| 5 | -9.6 | -9.87 | -10.48 | -11.15 | -11.85 | |||||||
| 6 | -11.5 | -12.08 | -12.71 | -13.38 | ||||||||
| 8 | -15.4 | -15.9 | -16.51 | |||||||||
| 10 | -19.2 | -19.73 | ||||||||||
| 12 | 23.01 | |||||||||||
Wanneer de buigradius groot is en de buighoek klein, is de mate van vervorming laag en ligt de neutrale laag dicht bij het midden van de plaatdikte.
Wanneer de buigradius (R) echter kleiner wordt en de buighoek (θ) toeneemt, neemt de mate van vervorming ook toe en beweegt de neutrale laag naar de binnenkant van het buigcentrum. De afstand van de neutrale laag tot de binnenkant van de plaat wordt aangeduid met λ, en de materiaaldikte wordt aangeduid met T.
De basisformule voor het berekenen van de ontvouwlengte:
Uitvouwlengte = binnenmaat van materiaal + binnenmaat van materiaal + hoeveelheid compensatie.
Je kunt ook de volgende calculator gebruiken om de uitgevouwen lengte van plaatmetaal te berekenen:

Hieronder worden de ontvouwalgoritmen van verschillende buigfuncties één voor één beschreven.
R = 0 mm, θ = 90° (Opmerking: Als R ≤ 1,0 mm, wordt het behandeld als R = 0 mm).
L = A + B + K
In de werkelijke productie kan de buigende bovenmatrijs een R-hoek dragen, of er kan een R-hoek van minder dan 1 mm zijn, of de keuze van de onderste matrijsDe V-groef kan onder andere groot zijn, wat resulteert in een kleine buigcoëfficiënt. Daarom wordt de buigcoëfficiënt van elke materiaalplaatdikte weergegeven in tabel 1 op basis van werkelijke empirische waarden.
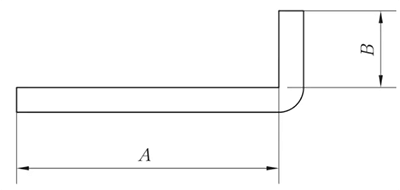
Fig. 1 Schematisch diagram van algemeen buigen I
R ≠ 0mm en θ = 90°
L = A + B + K (K is de booglengte van de neutrale laag)
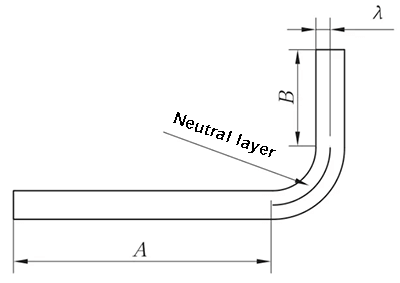
Fig. 2 Schematisch diagram van algemeen buigen II
R = 0 mm, θ ≠ 90°
L = A + B + K'
Opmerking: K is de compensatie bij 90°.
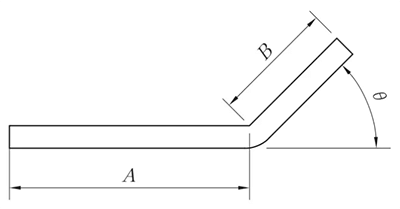
R ≠ 0mm, θ ≠ 90°
L = A + B + K
(K is de booglengte van de neutrale laag)
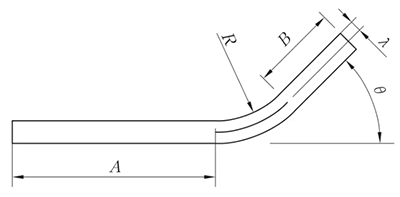
Fig. 4 Algemene buiging IV buigdiagram
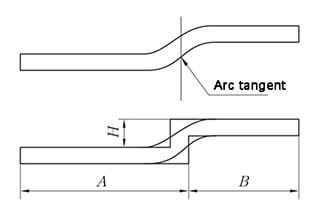
De uitvouwmethode is gelijkwaardig aan de Z-vouwmethode met evenwijdige rechte rand en de meting van de hoogte wordt gedemonstreerd in figuur 6.
De hoek θ wordt beschouwd als een 90° ontvouwing.
Voor 0 < T ≤ 1,6 mm is λ gelijk aan 0,5T.
Als T groter is dan 1,6 mm, is λ gelijk aan 0,4T.
Z-vouw, ook wel Offset buigenwordt gedifferentieerd in Offset buigen met rechte rand en Offset buigen met afgeschuinde rand op basis van de vormingshoek en de verwerkingsmethode wordt bepaald door de offsethoogte.
Als de offsethoogte, h, minder is dan 3,5 keer de dikte van het materiaal, offsetmatrijzen of verwisselbare matrijzen worden gebruikt voor het vormen.
Als de offsethoogte groter is dan 3,5 keer de materiaaldikte, wordt normaal positief en negatief vervormen toegepast.
Als de lengte van de afgeschuinde rand minder is dan 3,5 keer de materiaaldikte, worden offsetmatrijzen of wisselmatrijzen gebruikt voor het vormen.
Als de lengte van de afgeschuinde rand groter is dan 3,5 keer de materiaaldikte, wordt de normale één-positieve en één-negatieve vouw toegepast.
(1) Als H < 3,5T, alleen dan kan worden verwerkt door offset buigen.
L = A + B + H
(als H ≤ T, dan 0,2 mm compenseren)
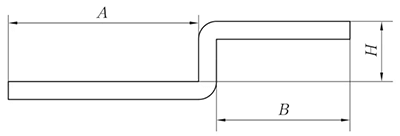
Fig. 5 Schematisch diagram van de richtliniaaloffset
(2) Niet-parallelle loodrechte afwijking
De expansiemethode is dezelfde als de parallelle Z-vouwmethode met rechte rand, en de hoogtewaarde wordt getoond in Figuur 6.
Hoek θ kan worden beschouwd als 90 ° ongevouwen.
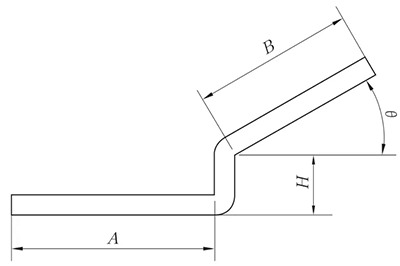
Fig. 6 Schematisch diagram van niet-parallelle richtliniaaloffset
(3) Rechte hoekverdraaiing - het overgangssegment raakt aan twee bogen
Wanneer de Straight-Edge Offset wordt ontvouwen op het raakpunt van twee cirkelbogen, wordt een verticale lijn gecreëerd op het raakpunt van de twee cirkelbogen op het buitenoppervlak van het substraat. Het materiaal wordt dan één materiaaldikte naar binnen verplaatst, zoals weergegeven in afbeelding 7, voor verwerking en ontvouwen met de Z-vouw 1 (Straight-Edge Offset) methode.
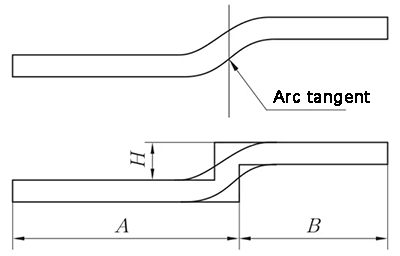
Fig. 7 Rechte hoek offset diagram - overgangssegment raakt aan twee cirkelbogen
Als H < 2T, is het ontvouwalgoritme als volgt volgens de offsetverwerking.
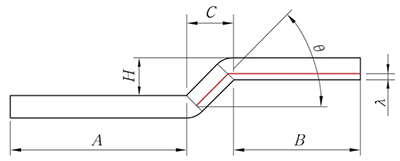
Fig. 8 Schema van afgeschuinde randoffset
L = A + B - K
(1) Overweeg bij het platdrukken om de lijn vóór het buigen aan te drukken op basis van de werkelijke omstandigheden.
De lijnpersplaats is in het midden van het buigvervormingsgebied.
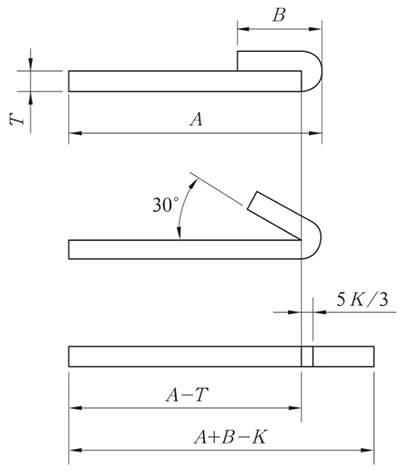
Fig. 9 Schematisch diagram van omgekeerd vouwen en pletten
Het omgekeerd vouwen en platdrukken gebeurt meestal in twee stappen: eerst wordt het materiaal gebogen tot 30° met de inlegmatrijs, gevolgd door het platdrukken.
Daarom moet bij het maken van de buiglijn Op de uitgebreide tekening is het essentieel om de buiglijn te illustreren op basis van de 150° buiging, zoals getoond in Figuur 9.
Tabel 1 buigcoëfficiënt van platen met verschillende diktes onder verschillende buighoeken
| Hoek | Dikte/mm | ||||
|---|---|---|---|---|---|
| 1 | 1.2 | 1.5 | 1.8 | 2.5 | |
| 45° | 5.3 | 6.3 | 7.8 | 9.5 | 13 |
| 50° | 4.5 | 5.4 | 6.8 | 8.1 | 11.25 |
| 55° | 4 | 4.7 | 5.8 | 7.05 | 9.75 |
| 60° | 3.4 | 4.1 | 5.1 | 6.15 | 8.5 |
| 65° | 3 | 3.6 | 4.5 | 5.4 | 7.5 |
| 70° | 2.65 | 3.2 | 4 | 4.75 | 6.6 |
| 75° | 2.35 | 2.8 | 3.5 | 4.25 | 5.9 |
| 80° | 2.1 | 2.5 | 3.1 | 3.75 | 5.25 |
| 85° | 1.9 | 2.25 | 2.8 | 3.35 | 4.65 |
| 90° | 1.7 | 2 | 2.5 | 3 | 4.15 |
| 95° | 1.5 | 1.8 | 2.2 | 2.7 | 3.75 |
| 100° | 1.35 | 1.6 | 2 | 2.4 | 3.35 |
| 105° | 1.2 | 1.4 | 1.75 | 2.15 | 3 |
| 110° | 1.1 | 1.3 | 1.6 | 2 | 2.65 |
| 115° | 1 | 1.25 | 1.4 | 1.7 | 2.35 |
| 120° | 0.85 | 1 | 1.25 | 1.5 | 2.1 |
| 125° | 0.75 | 0.9 | 1.1 | 1.35 | 1.85 |
| 130° | 0.65 | 0.8 | 1 | 1.18 | 1.65 |
| 135° | 0.55 | 0.7 | 0.85 | 1.05 | 1.45 |
| 140° | 0.5 | 0.6 | 0.75 | 0.9 | 1.25 |
| 145° | 0.43 | 0.5 | 0.65 | 0.77 | 1.05 |
| 150° | 0.35 | 0.43 | 0.55 | 0.65 | 0.9 |
| 155° | 0.3 | 0.35 | 0.45 | 0.53 | 0.75 |
| 160° | 0.23 | 0.27 | 0.35 | 0.4 | 0.6 |
| 165° | 0.17 | 0.2 | 0.25 | 0.3 | 0.45 |
De N-voudige verwerkingsmethode omvat zowel vervormen als afvlakken, en het algoritme voor ontvouwen is:
L = A + B + K
(K is de booglengte van de neutrale laag).
λ = 0,5T
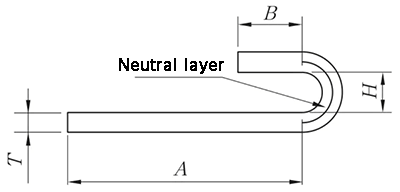
Fig.10 N-voudig diagram
(1) De booguitbreiding is direct K, en de booglengte van de neutrale laag is genomen. λ= 0,5T
(2) Uitbreiding met de rechte rand aan één kant.
L = A + K
(k is de booglengte van de neutrale laag)
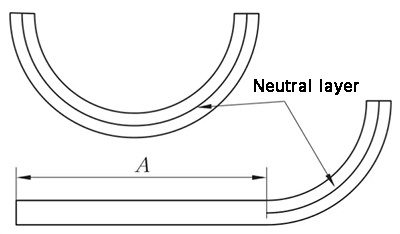
Fig. 11 Schematisch diagram van boogbuigen
In de werkelijke productie kan de nauwkeurige controle van de uitgevouwen lengte van plaatmetaal via 3D-software voornamelijk worden bereikt via de volgende stappen en methoden:
Kies de juiste 3D-ontwerpsoftware: Eerst moet je een 3D CAD software kiezen die geschikt is voor het ontwerpen van plaatwerk. SolidEdge, Creo, FreeCAD, UG, etc. zijn allemaal software die gebruikt kunnen worden voor het ontwerpen van plaatmetaal. Deze software biedt plaatmetaalmodules of gerelateerde functies die ontwerpers kunnen helpen met het ontwerp en de ontvouwingsberekeningen van plaatmetalen onderdelen.
Gebruik de plaatwerkmodule of gereedschappen in de software: De meeste 3D CAD software biedt gerelateerde gereedschappen en functies voor het ontwerpen van plaatwerk. Creo biedt bijvoorbeeld verschillende methoden voor het controleren van de uitgevouwen afmetingen van plaatmetaal, waaronder de modellerings- en uitvouwmethoden van grote plaatmetalen bogen, buigaftrekmethode, enz. FreeCAD, een open-source 3D modelleersoftware, biedt ook een plaatwerkmodule.
Apply ontvouwen berekeningsmethoden: Om de nauwkeurigheid van de lengte na het ontvouwen van het plaatmetaal te garanderen, kunnen verschillende ontvouwingsberekeningsmethoden worden gebruikt. Gangbare methoden zijn onder andere de buigcompensatiemethode, de buigaftrekmethode en de K-factorberekeningsmethode. Deze methodes kunnen ontwerpers helpen om de werkelijke lengte van het materiaal in ongevouwen toestand te berekenen, zodat de verwachte afmetingen van de onderdelen na het uiteindelijke buigen en vormen worden gegarandeerd.
Besteed aandacht aan het hanteren van randen en hoeken en het afstellen van details: Bij het ontwerpen van plaatwerk zijn de details van rand- en hoekafhandeling erg belangrijk. Sommige software, zoals SW, biedt verschillende oplossingen voor het verwerken van randen en hoeken en buigmethodes, die helpen om de vouwnauwkeurigheid te verbeteren.
Voor bochten die geen 90 graden zijn, zijn de gebruikelijke buighoeken 45 graden en 135 graden. De berekeningsmethode voor de K-factor is gebaseerd op de verhouding tussen de materiaaldikte en de buigradius.
Concreet betekent de K-factor δ / T, waarbij δ de materiaaldikte voorstelt en T de buigradius. Deze methode kan worden toegepast voor het berekenen van de buigcoëfficiënt van elke hoek die geen 90 graden is.
In praktische toepassingen wordt, vanwege de mogelijke verschillen en grote fouten in de aftrekwaarden van bochten onder verschillende hoeken, meestal de K-factor gebruikt als bochtencoëfficiënt.
Bovendien zijn er aanpassingen nodig om de K-factorwaarde van verschillende plaatdiktes nauwkeurig te leiden. Sommige referenties suggereren dat de K-factorwaarde voor elke buigradius kan worden berekend met behulp van specifieke interpolatietechnieken, die effectief zijn gebleken voor industriële plaattoepassingen.
De berekeningsformule voor de geëxpandeerde lengte van afgeschuind plaatwerk met persrem is: [L = A + B + C + 0,2], waarbij (A), (B) en (C) de interne afmetingen vertegenwoordigen en 0,2 dient als compensatiewaarde.
Gebaseerd op de algemene principes en praktijken van berekeningen van plaatuitzetting, houdt deze compenserende waarde rekening met afwijkingen tussen de werkelijke en theoretisch berekende lengtes door factoren zoals het buigen van materiaal en fouten in de matrijsprecisie tijdens echte bewerkingen.
Bij plaatbewerking helpt deze compensatiewaarde om de maatnauwkeurigheid en kwaliteit van het eindproduct te garanderen.
Plaatwerkonderdelen worden veel gebruikt in de elektromechanica, de lichte industrie en de auto-industrie.
De uitgevouwen vorm van plaatdelen is de belangrijkste bepalende factor voor de afmetingen van de blenk, die op hun beurt de afmetingen en vorm van de blenk beïnvloeden.
Traditionele methoden om plaatdelen uit te vouwen voldoen echter steeds minder aan de moderne ontwerpbehoeften vanwege hun lange cycli, lage efficiëntie en slechte kwaliteit.
Om deze tekortkomingen aan te pakken is het gebruik van geavanceerde CAD-systemen de laatste jaren steeds populairder geworden.
Deze gespecialiseerde systemen voor het ontwerpen van plaatmetalen onderdelen hebben een robuuste functionaliteit en kunnen de tijd en moeite die nodig zijn voor het voorontwerp en de implementatie van plaatmetalen onderdelen aanzienlijk verminderen.