Rechtheidsmeting: Rekenen als een professional

1. Inleiding

In de ingenieurspraktijk zijn er twee veelgebruikte methoden om de rechtheidsfout van geleiderails te evalueren: de methode van de tweezijdige puntverbinding en de methode van de minimale toestand.

De verbindingsmethode met twee eindpunten verbindt de foutencurve van begin tot eind, trekt vervolgens twee lijnen parallel aan de eind-tot-eindlijn op de hoogste en laagste punten van de curve en meet de waarden langs de verticale as tussen de twee parallelle lijnen.

Na gegevensverwerking is de waarde de rechtheidsfout van de geleiderail.

De minimumconditiemethode verbindt de "hoge, hoge" (of "lage, lage") punten van de foutencurve en trekt een lijn evenwijdig daaraan door het lage (hoge) punt.

De waarde gemeten tussen de twee parallelle lijnen langs de verticale as is de rechtheidsfout van de geleiderail na gegevensverwerking.

De minimumvoorwaardenmethode is een arbitrage-evaluatie.

De verbindingsmethode met twee eindpunten is geen arbitrage-evaluatie, maar wordt vaak gebruikt in de productie vanwege de eenvoud en het gemak bij de evaluatie, hoewel het soms grote fouten kan opleveren.

Dit artikel bespreekt de grenswaarde van de gegenereerde fout tussen deze twee evaluatiemethoden.

2. Foutcurve ligt aan dezelfde kant als beide uiteinden van de lijn

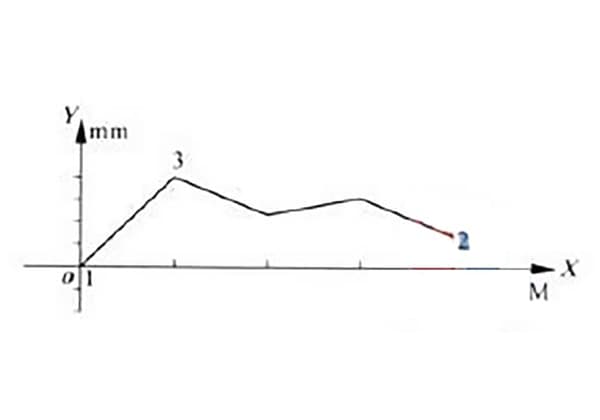
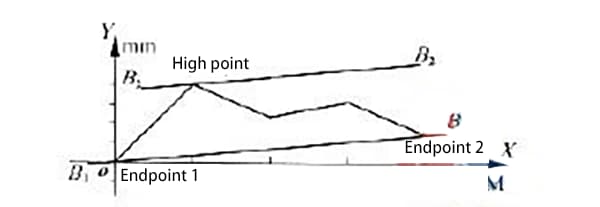
Door de rechtheidsfout van een bepaald model hydraulische geleider voor glijrails te meten, werd de rechtheidsfoutcurve verkregen zoals getoond in Figuur 1.

Zoals te zien is in de figuur, ligt de foutcurve aan dezelfde kant als beide uiteinden van de lijn.

Hieronder wordt de rechtheidsfoutwaarde van de geleiderail geëvalueerd met behulp van de minimumvoorwaardenmethode en de tweezijdige verbindingsmethode.

(1) Rechtheidsfout evalueren met de minimumvoorwaardenmethode

Volgens de minimumvoorwaardenmethode worden de laagste punten 1 en 2 van de kromme in figuur 1 (waarbij het laagste punt 1 samenvalt met de oorsprong) verbonden door de lijn a1a1 zoals weergegeven in figuur 2.

Door het hoogste punt 3 wordt evenwijdige lijn a2a2 getrokken ten opzichte van lijn a1a1.

De waarde gemeten langs de y-as in het gebied ingesloten door de twee parallelle lijnen a1a1 en a2a2, na verwerking van de gegevens, vertegenwoordigt de rechtheidsfout van de geleiderail δ verkregen met de minimumvoorwaardenmethode.

(2) Rechtheidsfout evalueren met behulp van de tweezijdige verbindingsmethode

Volgens de verbindingsmethode met twee uiteinden zijn de uiteinden van de kromme in Figuur 1 ook de eindpunten 1 en 2 van de kromme, zoals weergegeven in Figuur 3.

Eindpunten 1 en 2 worden verbonden door de lijn b1b1, en dan wordt een parallelle lijn b2b2 door het hoogste punt getrokken.

De waarde gemeten langs de y-as in het gebied ingesloten door de twee parallelle lijnen b1b1 en b2b2, na verwerking van de gegevens, vertegenwoordigt de rechtheidsfout van de geleiderail δ verkregen met de tweezijdige verbindingsmethode.

(3) Bepaling van de foutlimiet die door de twee evaluatiemethoden wordt gegenereerd

Aangezien beide evaluatiemethoden worden gebruikt om de rechtheidsfout van dezelfde geleiderail te bepalen, komen het "laagste punt 1", "laagste punt 2" en "hoogste punt 3" in figuur 2 respectievelijk overeen met het "laagste punt 1", "laagste punt 2" en "hoogste punt 3" in figuur 3. Hierdoor valt lijn a1a1 samen met lijn b1b1 en lijn a2a2 met lijn b2b2.

Daarom is de foutwaarde die door de twee evaluatiemethoden wordt gegenereerd nul.

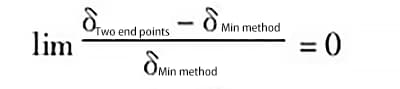
Op basis van de bovenstaande analyse is de foutlimiet die door de twee evaluatiemethoden wordt gegenereerd nul wanneer de foutcurve zich aan dezelfde kant bevindt als beide uiteinden van de lijn, wat betekent dat de evaluatieresultaten die door de twee methoden worden verkregen hetzelfde zijn.

3. Foutkromme ligt aan beide zijden van de lijn die de uiteinden verbindt

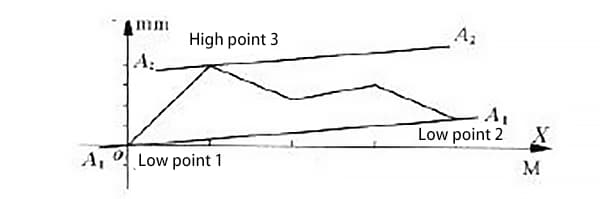
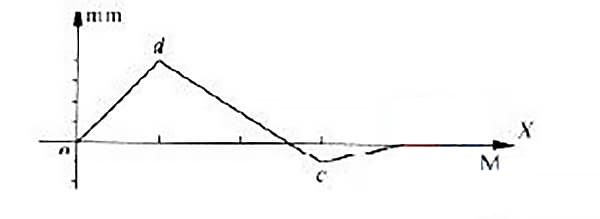
In de gemeten rechtheidsfoutenkromme van een geleiderail bevinden sommige foutkrommen zich aan beide zijden van de lijn die de uiteinden verbindt, zoals getoond in Figuur 4.

De foutkromme van deze geleiderail heeft een lijn die de uiteinden verbindt en die samenvalt met de x-as. De rechtheidsfout van de geleiderail wordt geëvalueerd met behulp van de minimumvoorwaardenmethode en de tweezijdige verbindingsmethode.

Zoals te zien is in Figuur 4, zijn de punten o en c de twee laagste punten en de twee eindpunten van de kromme, terwijl punt d het hoogste punt is.

Volgens de minimumvoorwaardenmethode worden de punten o en c verbonden door de lijn a1a1 zoals in figuur 5. De lijn a2a2 wordt evenwijdig met de lijn a1a1 door het hoogste punt d getrokken.

De waarde gemeten langs de y-as in het gebied ingesloten door de twee parallelle lijnen a1a1 en a2a2, na verwerking van de gegevens, vertegenwoordigt de rechtheidsfout van de geleiderail δ verkregen met de minimumvoorwaardenmethode.

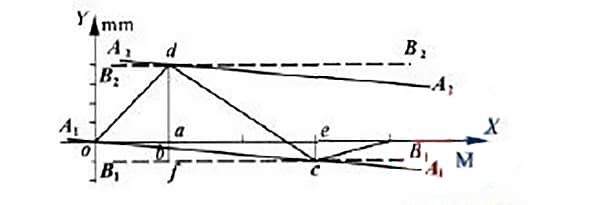
Trek volgens de tweepuntsverbindingsmethode twee lijnen evenwijdig aan de x-as door respectievelijk de punten C en D.

Deze lijnen worden voorgesteld door de stippellijnen b1b1 en b2b2 in figuur 5. In het gebied dat door deze twee parallelle lijnen wordt omsloten, vertegenwoordigt de waarde die na gegevensverwerking langs de y-as wordt gemeten de waarde van de rechtheidsfout van de geleiderail tussen de twee eindpunten.

Om de minimale afwijkingsmethode en de afwijkingswaarde in de twee eindpunten te bepalen, trek je een lijn evenwijdig aan de y-as door het punt D, snijdt de as in het punt A, snijdt de lijn a1a1 in het punt H en snijdt de lijn b1b1 in het punt F.

Trek op dezelfde manier een lijn evenwijdig aan de y-as door het punt C en snij de as in het punt E.

(1) Bepaling van de rechtheidsfout met behulp van de minimumvoorwaardenmethode

Volgens de minimumvoorwaardemethode wordt de rechtheidsfout δ van de geleiderail afgeleid uit de waarde gemeten langs de y-as na gegevensverwerking, wat de minimumafwijkingsmethode vertegenwoordigt.

Zoals getoond in Figuur 5:

En omdat BD = BA + AD,

∆OAB en ∆OEC zijn dus twee gelijkvormige driehoeken,

Als we vergelijking (3) herschikken, krijgen we:

Als we vergelijking (4) in vergelijking (2) substitueren en herschikken, krijgen we:

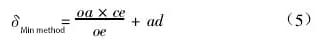
(2) Bepaling van de rechtheidsfout met behulp van de tweepuntsverbindingsmethode

Volgens de tweepuntsverbindingsmethode vertegenwoordigt de gemeten waarde langs de y-as na gegevensverwerking de foutwaarde δ van de rechtheid van de geleiderail tussen de twee eindpunten.

Zoals getoond in Figuur 5:

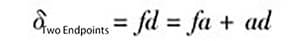
En aangezien fa = ce,

(3) Berekening van foutwaarden gegenereerd door twee evaluatiemethoden

Vergelijking (6) min vergelijking (5), dus,

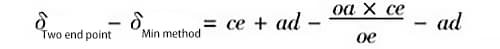
Als we herschikken, krijgen we:

(4) Berekening van de maximale fout door twee evaluatiemethoden

Stel in figuur 5 dat ad = δ1, ce = δ2, oa = p; stel dat de lengte van de te meten geleiderail l is, dan is oe = l - p, en:

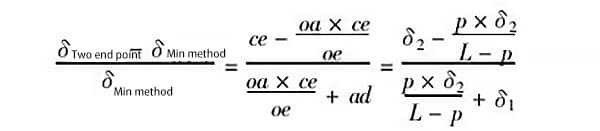
Wanneer bijvoorbeeld p = 0,5m (d.w.z. de verticale hoek is 0,5m), δ1 = 1,0δ, δ2 = 0,25δ, en de lengte van de gemeten geleiderail is l - 2m, dan is de foutverhouding die door de twee evaluatiemethoden wordt gegenereerd:

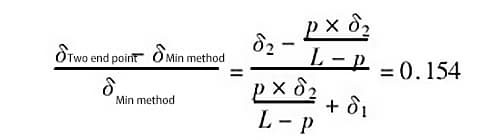
De verhouding van de fout die door de twee evaluatiemethoden wordt gegenereerd is 0,154, wat betekent dat de fout die door de tweepuntsverbindingsmethode wordt gegenereerd 15,4% groter is dan de fout die door de minimumvoorwaardenmethode wordt gegenereerd.

In de bovenstaande vergelijking, wanneer d.w.z. dat het hoogste en laagste punt van de foutencurve oneindig ver uit elkaar liggen, dan isdus krijgen we:

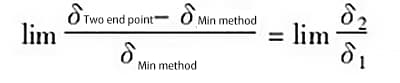
Wanneer bijvoorbeeld δ1 = 1,0δ en δ2 = 0,25δ en de afstand tussen het hoogste en laagste punt van de foutencurve oneindig groot is (d.w.z. L=0,25), dan is de verhouding van de door de twee evaluatiemethoden gegenereerde fout , wat betekent dat de fout die gegenereerd wordt door de tweepuntsverbindingsmethode 25% groter is dan de fout die gegenereerd wordt door de minimumvoorwaardenmethode.

Wanneer δ1 = δ2, d.w.z. de afstand tussen het hoogste en het laagste punt van de foutencurve gelijk is, zoals weergegeven in figuur 6, dan zijn de maximale foutwaarden die door de twee evaluatiemethoden worden gegenereerd:

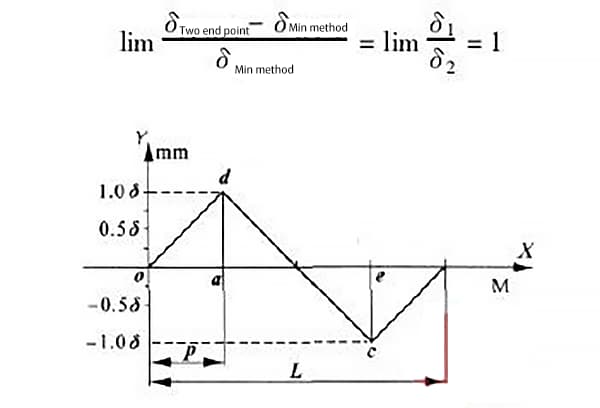
Hieruit kan worden afgeleid dat wanneer het hoogste en laagste punt van de geleiderail gelijk zijn en oneindig ver uit elkaar liggen, de maximale fout die door de twee evaluatiemethoden wordt gegenereerd het grootst is en 100% kan bereiken.

Tabel 1 toont de verhouding van de fouten gegenereerd door de twee evaluatiemethoden voor verschillende lengtes van de gemeten geleiderail, wanneer de punten van de foutencurve verdeeld zijn aan beide zijden van de tweepunts verbindingslijn.

De afstand tussen het hoogste en laagste punt van de foutencurve is gelijk als de meetafstand p = 0,5.

Tabel 1 Foutverhouding van twee evaluatiemethoden

Foutverhouding	Afstand L (M) tussen het hoogste en laagste punt van de geleiderail
1	10	15	20	25	30	40	∞
	33.30%	90%	93.30%	95%	96%	96.70%	97.50%

4. Conclusie

Als de punten op de rechtheidsfoutenkromme aan dezelfde kant van de tweepuntsverbindingslijn liggen, dan zijn de fouten die door de twee evaluatiemethoden worden gegenereerd nul, d.w.z. de resultaten van de twee evaluatiemethoden zijn hetzelfde.

Als de punten op de rechtheidsfoutenkromme aan beide zijden van de tweepuntsverbindingslijn liggen en de hoogste en laagste punten van de foutenkromme gelijk zijn en oneindig ver uit elkaar liggen, dan is de maximale fout die door de twee evaluatiemethoden wordt gegenereerd de grootste en kan de fout die door de tweepuntsverbindingsmethode wordt gegenereerd 100% hoger zijn dan de fout die door de minimumvoorwaardenmethode wordt gegenereerd.

Daarom is het bij het evalueren van de rechtheidsfout van geleiderails van grote bewerkingsmachines in de praktijk erg belangrijk om de juiste evaluatiemethode te kiezen. Als de punten op de foutkromme aan beide zijden van de tweepuntsverbindingslijn liggen, moet de methode van de minimale voorwaarde als eerste keuze voor evaluatie worden gebruikt.