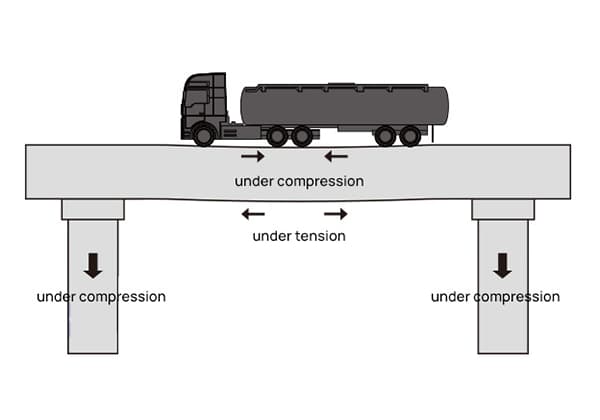
Stel je voor dat je op een brug staat en een zware vrachtwagen voorbij ziet rijden. Heb je je ooit afgevraagd waarom de brug niet instort onder het gewicht? Dit artikel duikt in de concepten van rek en spanning, legt uit hoe materialen vervormen onder kracht en hoe ingenieurs deze vervormingen berekenen om de veiligheid te garanderen. Je leert de fundamentele relaties tussen deze krachten, hoe ze gemeten worden en hun praktische implicaties in alledaagse constructies. Of je nu een aankomend ingenieur bent of gewoon nieuwsgierig, deze gids zal licht werpen op de onzichtbare krachten die onze wereld intact houden.

Ten eerste meet het merendeel van de veiligheidsmonitoringindustrie de vervorming van de structuur die wordt getest. Te veel vervorming kan ongelukken veroorzaken.
Scheuren in constructies, verzakkingen en verplaatsingen tussen de constructie en een vaste referentie zijn bijvoorbeeld grote vervormingen die met het blote oog kunnen worden waargenomen en in millimeters kunnen worden gemeten met meetinstrumenten zoals scheurmeters, statische niveaus en verplaatsingsmeters.
Maar hoe kan de kleine vervorming die wordt veroorzaakt door compressie binnen de te testen constructie of door buiging buiten het balkvormige object worden weergegeven?
Het antwoord is spanning.

Stel dat de lengte van een constructie met lengte L vervormt onder spanning en de lengte verandert in L', dan is de verandering in lengte ΔL = L' - L, en de rek ε is de verhouding van de verandering in lengte ΔL tot de oorspronkelijke lengte L, de formule is als volgt:

Wat is dan de eenheid van spanning?
Zoals uit de formule blijkt, is rek een verhouding en dimensieloos, wat betekent dat het geen eenheid heeft.
Wat is microstress?
Omdat ΔL erg klein is, meestal in het micronbereik, is de berekende spanningswaarde erg klein, met veel cijfers achter de komma, wat het lastig maakt om weer te geven en te bekijken. Daarom is de wetenschappelijke notatie 10-6 geïntroduceerd, microspanning με genaamd, die kan worden begrepen als de eenheid van microspanning is 10-6 en ons meetbereik van de spanningsmeter is ±1500 microspanning, positief geeft uitrekken aan en negatief geeft compressie aan.
Vervorming is een kleine vervorming in de structuur die wordt getest, dus waarom vervormt deze? Omdat er een externe kracht op wordt uitgeoefend.
Als we een brugpijler als voorbeeld nemen en er rijdt een volgeladen vrachtwagen op de brug, dan zal de pier extra druk dragen en samendrukking en samendrukking produceren, terwijl de pier een interne kracht zal produceren om de externe kracht tegen te gaan en de vervorming te overwinnen.
Deze interne kracht is spanning. Spanning wordt gedefinieerd als de kracht per oppervlakte-eenheid, wat eigenlijk druk is, met eenheden van MPa.
Dus wat is het verband tussen de variabele voor rek en de verandering in spanning die wordt verdragen? Bekijk de berekeningsformule:

In de formule staat σ voor spanning en E voor de elasticiteitsmodulus van het geteste materiaal, ook bekend als Young's modulus, een fysische grootheid die de elasticiteit van het materiaal beschrijft.
Het kan worden gezien als het vermogen van het materiaal om vervorming te weerstaan (stijfheid) en vanuit microperspectief is het de bindingssterkte tussen atomen en moleculen.
Twee materialen met dezelfde vervorming (dezelfde rekwaarde), het materiaal met een hogere weerstand tegen vervorming (een grotere elasticiteitsmodulus) zal een grotere spanning verdragen.
Als bijvoorbeeld tofu en een ijzeren blok van dezelfde grootte 1 mm in hoogte worden samengedrukt, hoeft de eerste slechts voorzichtig met de hand te worden aangedrukt, terwijl de laatste moet worden geholpen door een gereedschap.
De elasticiteitsmodulus van gewone technische materialen is te vinden in tabellen, zoals de elasticiteitsmodulus van C30-beton 30000MPa (1N/mm2 = 1MPa) en de elasticiteitsmodulus van koolstofstaal is 206GPa.
De elasticiteitsmodulus Ec van beton onder druk en spanning moet worden aangenomen volgens tabel 4.1.5.
De afschuifmodulus Gc van beton kan worden aangenomen op 40% van de overeenkomstige elasticiteitsmoduluswaarde.
De Poisson's ratio Vc van beton kan worden aangenomen op 0,2.
Tabel4.15 Elastische modulus van beton (×104N/mm2).
| Betonsterkte graad | C15 | C20 | C25 | C30 | C35 | C40 | C45 | C50 | C55 | C60 | C65 | C70 | C75 | C80 |
| Ec | 2.20 | 2.55 | 2.80 | 3.00 | 3.15 | 3.25 | 3.35 | 3.45 | 3.55 | 3.60 | 3.65 | 3.70 | 3.75 | 3.80 |
Opmerking:
1. Als er betrouwbare testgegevens beschikbaar zijn, kan de elasticiteitsmodulus worden bepaald op basis van werkelijk gemeten gegevens;
2. Wanneer een grote hoeveelheid minerale hulpstoffen aan beton wordt toegevoegd, kan de elasticiteitsmodulus worden bepaald op basis van actuele meetgegevens volgens de gespecificeerde leeftijd.
Tabel 1.1-13 Elastische modulus en Poisson's ratio van veelgebruikte materialen
| Item | Elastische modulus E/GPa | Afschuifmodulus G/GPa | Poisson's ratio μ | Item | Elastische modulus E/GPa | Afschuifmodulus G/GPa | Teflon |
| Grijs gietijzer | 118~126 | 44.3 | 0.3 | Gewalst zink | 82 | 31.4 | 0.27 |
| Nodulair gietijzer | 173 | 0.3 | Lood | 16 | 6.8 | 0.42 | |
| Koolstofstaal, nikkelchroomstaal | 206 | 79.4 | 0.3 | Glas | 55 | 1.96 | 0.25 |
| Gelegeerd staal | Organisch glas | 2.35-29.42 | |||||
| Gietstaal | 202 | 0.3 | Rubber | 0.0078 | 0.47 | ||
| Gewalst zuiver koper | 108 | 39.2 | 0.31-0.34 | Bakeliet | 1.96-2.94 | 0.69-2.06 | 0.35-0.38 |
| Koudgetrokken zuiver koper | 127 | 48.0 | Sandwich fenol plastic | 3.92-8.83 | |||
| Gewalst fosfor-tintbrons | 113 | 41.2 | 0.32-0.35 | Celluloid | 1.71-1.89 | 0.69-0.98 | 0.4 |
| Koudgetrokken messing | 89-97 | 34.3-36.3 | 0.32-0.42 | Nylon 1010 | 1.07 | ||
| Gewalst mangaanbrons | 108 | 39.2 | 0.35 | Niet-geplastificeerd polyvinylchloride | 3.14-3.92 | 0.35-0.38 | |
| Gewalst aluminium | 68 | 25.5-26.5 | 0.32-0.36 | teflon | 1.14-1.42 | ||
| Getrokken aluminium draad | 69 | Lage druk polyethyleen | 0.54-0.75 | ||||
| Gegoten aluminium brons | 103 | 41.1 | 0.3 | Hoge druk polyethyleen | 0.147-0.245 | ||
| Gegoten tinbrons | 103 | 0.3 | beton | 13.73~39.2 | |||
| Duraluminiumlegering | 70 | 26.5 | 0.3 | 4.9-15.69 | 0.1-0.18 |
Immers, als inwendige spanningen niet direct kunnen worden gemeten, kan de spanning worden berekend door de rek te meten en deze vervolgens te vermenigvuldigen met de elasticiteitsmodulus van het materiaal.