In dit artikel verkennen we de fascinerende concepten van sterkte en stijfheid in de techniek. Je leert hoe deze principes zorgen voor de veiligheid en duurzaamheid van alledaagse voorwerpen, van bruggen tot smartphoneschermen. Ontdek samen met ons de geheimen achter de wonderen der techniek!
Om de optimale prestaties en betrouwbaarheid van een mechanisch systeem of constructie te garanderen, moet elk onderdeel zijn beoogde functie effectief en efficiënt vervullen. Het primaire doel van het ontwerp van de veiligheid van technische componenten is om te garanderen dat alle elementen voldoende sterk, stijf en stabiel zijn, zodat de algehele integriteit en levensduur van het systeem gewaarborgd zijn.
Stabiliteit is een fundamenteel concept in engineering, dat verwijst naar het vermogen van een component om zijn oorspronkelijke evenwichtstoestand te behouden of terug te krijgen wanneer het wordt blootgesteld aan externe krachten. Dit principe is cruciaal in verschillende scenario's, zoals:
Deze voorbeelden illustreren het belang van stabiliteit bij het voorkomen van catastrofale storingen en het waarborgen van de veilige werking van mechanische systemen en constructies.
In deze discussie zal ik me richten op het verduidelijken van mijn uitgebreide begrip van twee even cruciale engineeringprincipes: stijfheid en sterkte. Samen met stabiliteit vormen deze concepten de drie-eenheid van fundamentele overwegingen bij het ontwerpen van veiligheidscomponenten, die elk een essentiële rol spelen bij het bepalen van de algemene prestaties, duurzaamheid en veiligheid van technische systemen.
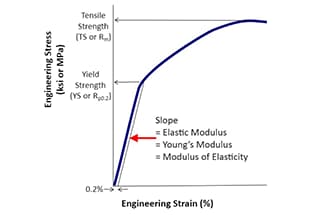
Definitie: Sterkte is het vermogen van materialen, onderdelen of structuren om toegepaste belastingen of krachten te weerstaan zonder falen, overmatige vervorming of schade. Het is een fundamentele eigenschap in materiaalkunde en engineering die het vermogen van een materiaal om mechanische spanning te weerstaan bepaalt.
Kracht omvat verschillende aspecten, waaronder:
Bij metaalproductie is inzicht in de sterkte van materialen bijvoorbeeld cruciaal voor het ontwerpen van onderdelen die bestand zijn tegen operationele belastingen. Een stalen balk in een gebouw moet voldoende sterk zijn om het gewicht van de constructie en extra belastingen te dragen zonder te buigen of te breken.
Sterkte wordt beïnvloed door verschillende factoren, waaronder:
De maateenheid voor sterkte wordt meestal uitgedrukt in megapascal (MPa) of pounds per square inch (psi) in imperiale eenheden. Zo heeft zacht staal een treksterkte van ongeveer 400-550 MPa, terwijl hoogsterkte gelegeerde staalsoorten 1000 MPa kunnen overschrijden.
In de productie en engineering zijn sterkteberekeningen en -testen essentieel voor:
Geavanceerde technieken zoals eindige-elementenanalyse (FEA) en destructieve testen worden vaak gebruikt om de sterkte van materialen en componenten in complexe technische toepassingen te beoordelen en te valideren.
Brosse breuk: Een plotselinge en catastrofale bezwijkmodus die gekenmerkt wordt door snelle scheurgroei met minimale plastische vervorming. Dit type breuk treedt op zonder waarschuwing en resulteert meestal in een schoon, vlak breukvlak.
Bijvoorbeeld:
Plastic opbrengst: Een faalwijze waarbij het materiaal een aanzienlijke plastische vervorming ondergaat, wat resulteert in een permanente vormverandering en verlies van structurele integriteit. Dit type bezwijken is over het algemeen geleidelijker en beter waarneembaar dan brosse breuk.
Bijvoorbeeld:
Het is belangrijk op te merken dat de bezwijkmodus van een materiaal afhangt van verschillende factoren, waaronder materiaaleigenschappen, belastingsomstandigheden, temperatuur en omgevingsfactoren. Sommige materialen kunnen een overgang vertonen van taai naar bros gedrag onder bepaalde omstandigheden, zoals lage temperaturen of hoge reksnelheden.
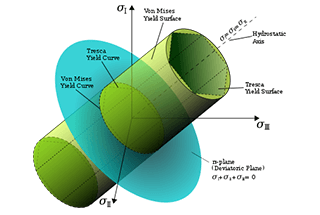
1. Theorie van de maximale trekspanning:
Wanneer de maximale trekspanning σ1 op een punt in het onderdeel de uiterste spanning σb bereikt onder unidirectionele spanningscondities, zal het materiaal brosse breuk ondergaan. Aldus zijn de criteria voor brosse breuk van onderdelen met kritische punten onder complexe spanningscondities: σ1 = σb.
Bijgevolg zijn de sterktevoorwaarden die door de eerste sterktetheorie zijn: σ1 ≤ σb.
2. Theorie van de maximale trekspanning:
Wanneer de maximale trekrek ε1 de grenswaarde εu bereikt onder unidirectionele spanning, zal het materiaal bezwijken door brosse breuk. Dit kan worden uitgedrukt als ε1 = εu.
Uit de veralgemeende Wet van Hooke kunnen we ε1 berekenen als: ε1 = [σ1 - u(σ2 + σ3)] / E, dus σ1 - u(σ2 + σ3) = σb.
De sterktevoorwaarden vastgesteld door de tweede sterktetheorie zijn: σ1 - u(σ2 + σ3) ≤ σb.
3. Theorie van maximale schuifspanning:
Wanneer de maximale schuifspanning τMax de uiterste schuifspanning τ0 bereikt onder unidirectionele spanningsomstandigheden, zal het materiaal bezwijken door vloeien. Dit kan worden uitgedrukt als τMax = τ0.
De formule voor de schuifspanning op een schuine doorsnede tijdens axiale spanning is τ0 = σs/2 (σs is de normaalspanning op de doorsnede). De formule voor τMax is (σ1 - σ3)/2. De schadeconditie kan dus worden herschreven als σ1 - σ3 = σs.
De sterktevoorwaarde vastgesteld door de derde sterktetheorie is: σ1 - σ3 ≤ σs.
4. Vormverandering specifieke energietheorie:
Wanneer de vormveranderingsverhouding op een punt in het onderdeel de grenswaarde bereikt onder unidirectionele spanningscondities, zal het materiaal bezwijken als gevolg van doorbuiging.
De sterktevoorwaarde vastgesteld door de vierde sterktetheorie is:
√(σ1^2 + σ2^2 + σ3^2 - σ1σ2 - σ2σ3 - σ3σ1) < σs.
Definitie: Stijfheid verwijst naar het vermogen van een materiaal, onderdeel of constructie om elastische vervorming of verplaatsing te weerstaan wanneer er een externe kracht op wordt uitgeoefend. Het kwantificeert de mate waarin een systeem zijn vorm en afmetingen binnen toelaatbare grenzen kan behouden onder toegepaste belastingen.
Stijfheid is een fundamentele parameter in engineering die de relatie tussen kracht en vervorming in een materiaal of constructie karakteriseert. Het wordt gedefinieerd als de verhouding tussen de toegepaste kracht en de resulterende verplaatsing en geeft de hoeveelheid kracht aan die nodig is om een eenheid van vervorming te veroorzaken. In wiskundige termen wordt stijfheid (k) uitgedrukt als:
k = F / δ
Waar:
De eenheid van stijfheid is meestal kracht per lengte-eenheid, zoals N/m (Newton per meter) in het SI-stelsel of lbf/in (pounds-force per inch) in het imperiale stelsel.
In praktische termen kan stijfheid worden geconceptualiseerd met behulp van de analogie van een veer. De veerconstante, die de stijfheid van een veer weergeeft, wordt gedefinieerd als de verhouding tussen de uitgeoefende trek- of drukkracht en de resulterende rek of samendrukking. Deze relatie wordt beschreven door de Wet van Hooke voor lineair elastische systemen.
Het begrijpen en beheersen van stijfheid is cruciaal in verschillende technische toepassingen, waaronder:
Ingenieurs moeten de stijfheidseisen afwegen tegen andere ontwerpoverwegingen zoals sterkte, gewicht, kosten en produceerbaarheid om optimale oplossingen te creëren voor specifieke toepassingen.
Wanneer de toegepaste belasting constant is, wordt dit statische stijfheid genoemd.
Wanneer de belasting wisselt, wordt dit dynamische stijfheid genoemd.
Statische stijfheid omvat structurele stijfheid en contactstijfheid.
Structurele stijfheid verwijst naar de stijfheid van het onderdeel zelf en omvat buigstijfheid en torsiestijfheid.
1. Buigstijfheid: berekend volgens de volgende formule:
K=P/δ
Waar
2. De torsiestijfheid wordt berekend met de volgende formule:
Km=ML/θ
Waarbij M - toegepast koppel (n - m);
L - afstand van de positie van de koppelactie tot het vaste uiteinde (m);
θ-- Torsiehoek (°)
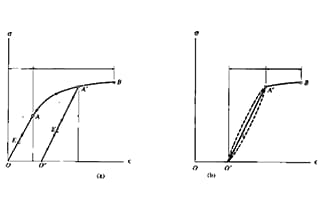
Uit de bovenstaande uitleg van sterkte en stijfheid blijkt dat sterkte zich richt op bezwijken onder externe kracht en wordt ingedeeld in plastische rek en brosse breuk bezwijken, wat gerelateerd is aan de spanning-rek curve tijdens trekproeven. Stijfheid heeft daarentegen betrekking op de relatie tussen vervorming en kracht.
Zoals weergegeven in fig.
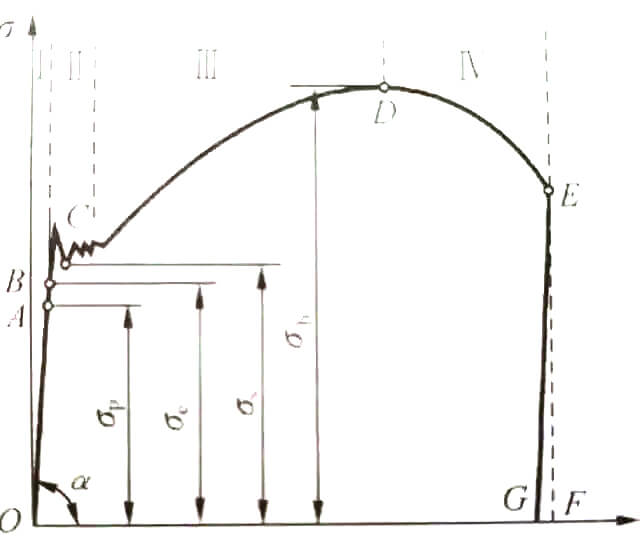
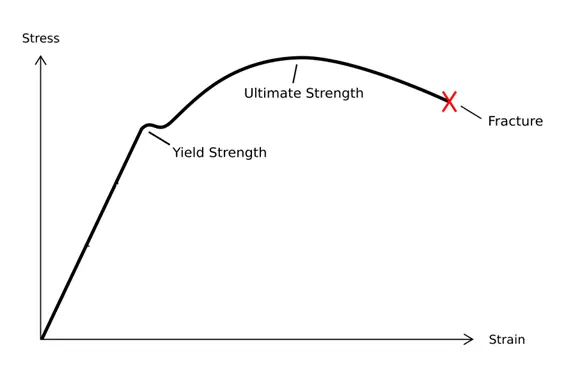
De curve in de figuur kan worden onderverdeeld in vier fasen:
1. Elastische vervormingsfase;
2. Opbrengststadium;
3. Versterkende fase;
4. Plaatselijke nekfase.
Stijfheid wordt gedefinieerd als weerstand tegen elastische vervorming, die optreedt in het beginstadium en wordt bepaald door de wet van Hooke onder elastische omstandigheden.
Berekening van de buigstijfheid en torsiestijfheid onder statische belastingen is vergelijkbaar met de wet van Hooke, wat suggereert dat stijfheid alleen wordt gemeten tijdens de elastische vervormingsfase.
In het volgende stadium, wanneer plastische vervorming optreedt tijdens trekproeven, verdwijnt de restrek niet. Op de spanning-rek kromme blijft de spanning bijna onveranderd, maar de rek neemt aanzienlijk toe. Op dit punt bereikt de spanning de vloeigrens en komt het materiaal in de fase van plastische vloeivervorming. Naarmate de spanning blijft toenemen, neemt ook de rek toe tot deze de vloeigrens bereikt.
Daarom vindt de meting van de sterkte plaats nadat het materiaal elastische vervorming heeft ondergaan en voordat het de sterktegrens bereikt.
Concluderend kan gesteld worden dat zowel stijfheid als sterkte geëvalueerd worden tijdens de bezwijkfase van onderdelen, waarbij stijfheid gemeten wordt aan de hand van spanning en sterkte aan de hand van vervorming.
In termen van hun volgorde in het vervormingsproces treedt stijfheid op in de vroegere fase terwijl sterkte in de latere fase optreedt.
Vandaar dat bij het evalueren van de bezwijkcondities van onderdelen, zolang aan de stijfheidsvereisten wordt voldaan, het onderdeel voldoende spanning moet kunnen weerstaan tijdens de elastische vervormingsfase, die op zijn beurt moet voldoen aan de sterktevereisten.
Deze relatie wordt weerspiegeld in verschillende ontwerpen, zoals de as in mechanische apparatuur. Gewoonlijk wordt de asmaat bepaald op basis van sterktevoorwaarden en vervolgens wordt de stijfheid geverifieerd op basis van stijfheidsvoorwaarden.
Daarom worden de stijfheidseisen voor precisiemachineassen zeer hoog gesteld en wordt het ontwerp van de dwarsdoorsnede vaak bepaald door stijfheidsvoorwaarden.
Als oprichter van MachineMFG heb ik meer dan tien jaar van mijn carrière gewijd aan de metaalbewerkingsindustrie. Door mijn uitgebreide ervaring ben ik een expert geworden op het gebied van plaatbewerking, verspaning, werktuigbouwkunde en gereedschapsmachines voor metalen. Ik denk, lees en schrijf voortdurend over deze onderwerpen en streef er voortdurend naar om voorop te blijven lopen in mijn vakgebied. Laat mijn kennis en expertise een aanwinst zijn voor uw bedrijf.
NL 
EN 
AR 
DE 
ES 
FR 
IT 
JA 
PT 
PT_BR 
RU 
KO