De vloeigrens, een cruciale maar vaak over het hoofd geziene eigenschap, speelt een cruciale rol bij de materiaalselectie. In dit artikel verdiepen we ons in de grondbeginselen van vloeigrens en onderzoeken we het belang ervan in de machinebouw. Ontdek hoe dit essentiële concept de wereld om ons heen vormgeeft en krijg waardevolle inzichten van industrie-experts.
Opbrengststerkte: Het is de opbrengstlimiet van een metaalmateriaal wanneer het bezwijkt, d.w.z. de spanning die een lichte plastische vervorming weerstaat.
Voor metalen materialen zonder duidelijke rekking, wordt de spanningswaarde die 0,2% restvervorming veroorzaakt gespecificeerd als de vloeigrens, de voorwaardelijke vloeigrens of de vloeigrens genoemd.
Externe krachten groter dan deze limiet zullen leiden tot het permanent falen van het onderdeel en kunnen niet hersteld worden. De vloeigrens van staal met een laag koolstofgehalte is bijvoorbeeld 207 MPa.
Wanneer externe krachten groter zijn dan deze limiet, zal het onderdeel permanent vervormen. Als de vervorming kleiner is, zal de component terugkeren naar zijn oorspronkelijke vorm.
De vloeigrens speelt een centrale rol in de materiaalkunde en engineering en dient als een kritische parameter in ontwerpmethodologieën en materiaalselectieprocessen. In traditionele sterkteontwerpbenaderingen is de vloeigrens de maatstaf voor taaie materialen, waarbij de toelaatbare spanning wordt gedefinieerd als [σ] = σys/n, waarbij σys de vloeigrens is en n de veiligheidsfactor. Deze veiligheidsfactor varieert gewoonlijk van 1,1 tot 2 of hoger, afhankelijk van specifieke toepassingsvereisten en bedrijfsomstandigheden.
Voor brosse materialen, die geen duidelijk vloeipunt hebben, wordt de uiterste treksterkte (σb) als referentie gebruikt, waarbij de toelaatbare spanning wordt berekend als [σ] = σb/n. In deze gevallen wordt over het algemeen een meer conservatieve veiligheidsfactor (n) van ongeveer 6 gebruikt om rekening te houden met de beperkte plastische vervormingscapaciteit van het materiaal en de plotselinge bezwijkmodus.
Het is cruciaal om te erkennen dat terwijl de traditionele op sterkte gebaseerde ontwerpmethodologie vaak leidt tot een focus op het maximaliseren van de vloeigrens, deze aanpak onbedoelde gevolgen kan hebben. Als de vloeigrens toeneemt, is er vaak een overeenkomstige afname in breuktaaiheid, waardoor het risico op catastrofaal falen mogelijk toeneemt. Deze omgekeerde relatie onderstreept het belang van gebalanceerde optimalisatie van materiaaleigenschappen in plaats van een focus op de vloeigrens.
Het belang van vloeigrens reikt verder dan de directe toepassing in spanningsberekeningen. Het dient als een waardevolle indicator voor het voorspellen van verschillende mechanische gedragingen en verwerkingseigenschappen van materialen in technische toepassingen. Bijvoorbeeld:
Stress
Wanneer een voorwerp vervormt door externe factoren (krachten, vochtigheid, temperatuursveranderingen, enz.), zijn er interne krachten die een wisselwerking aangaan tussen de verschillende delen van het voorwerp. De interne kracht per oppervlakte-eenheid wordt spanning genoemd.
Deze loodrecht op de doorsnede worden normale spanning of axiale spanning genoemd en deze die de doorsnede raken worden schuifspanning of snijspanning genoemd.
Stam
Vervorming verwijst naar de relatieve vervorming van een object onder invloed van externe krachten en niet-uniforme temperatuurvelden, naast andere factoren.
Volgens de wet van Hooke hebben spanning en rek binnen een bepaald proportioneel grensbereik een lineair evenredig verband.
De bijbehorende maximale spanning wordt de proportionele limiet genoemd.
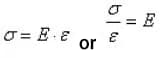
De verhouding tussen spanning en rek, aangeduid met E, wordt de elasticiteitsmodulus of Young-modulus genoemd en verschillende materialen hebben een vaste Young-modulus.
Hoewel spanning niet direct gemeten kan worden, kan het berekend worden door de rek te meten die veroorzaakt wordt door externe krachten.
Aanvullende informatie
De wet van Hooke is een basiswet in de theorie van mechanische elasticiteit, die stelt dat vaste materialen een lineair verband hebben tussen spanning en rek (vervorming per eenheid) wanneer ze aan spanning worden onderworpen.
Materialen die voldoen aan de wet van Hooke worden lineair elastische of Hookeïsche materialen genoemd.
De uitdrukking van de wet van Hooke is F=k-x of ΔF=k-Δx, waarbij k een constante is, de stijfheidscoëfficiënt van het voorwerp.
In het Internationaal Stelsel van Eenheden is de eenheid van F Newton, de eenheid van x meter en het is een vervormingsvariabele (elastische vervorming) en de eenheid van k is Newton/meter.
De stijfheidscoëfficiënt is numeriek gelijk aan de veerkracht wanneer de veer wordt uitgerekt (of ingekort) met een eenheidslengte.
Wat zijn de soorten stress?
Normale spanning: De spanningscomponent loodrecht op de doorsnede wordt normale spanning (of axiale spanning) genoemd en wordt aangeduid met σ.
Normale spanning vertegenwoordigt het uitrekken en samendrukken tussen aangrenzende doorsneden binnen het onderdeel.
Normale rek: De normaalrek op een punt is de rek langs de richting van de normaalkracht als gevolg van de normaalspanning verdeeld over de doorsnede in die richting.
Schuifspanning: De spanningscomponent die tangentieel is aan de doorsnede wordt schuifspanning of schuifkracht genoemd, aangeduid met τ. Schuifspanning vertegenwoordigt de schuifwerking tussen twee delen.
Schuifspanning: De afschuifspanning op een punt is de verandering in hoek tussen twee loodrechte richtingen als gevolg van de afschuifspanning verdeeld over de doorsnede. Het is ook bekend als afschuifvervorming.
Wat zijn de soorten spanning?
Er zijn voornamelijk twee soorten rek: lineaire rek en hoekrek. Lineaire rek, ook wel normale rek genoemd, is de verhouding van de toename in lengte (positief bij rek) van een klein lijnstuk in een bepaalde richting ten opzichte van de oorspronkelijke lengte.
Hoekvervorming, ook bekend als afschuifspanning of afschuifvervorming, is de verandering in hoek (positief bij afname) tussen twee loodrechte lijnsegmenten als gevolg van de afschuifspanning. Het wordt uitgedrukt in radialen.
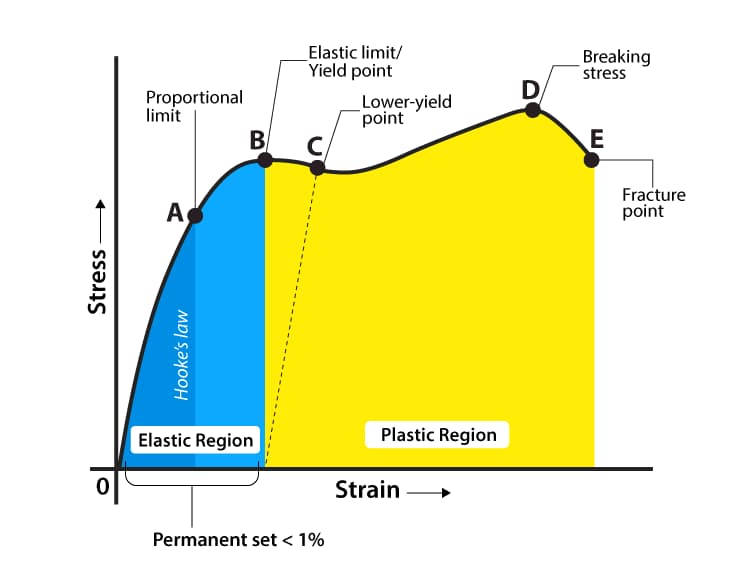
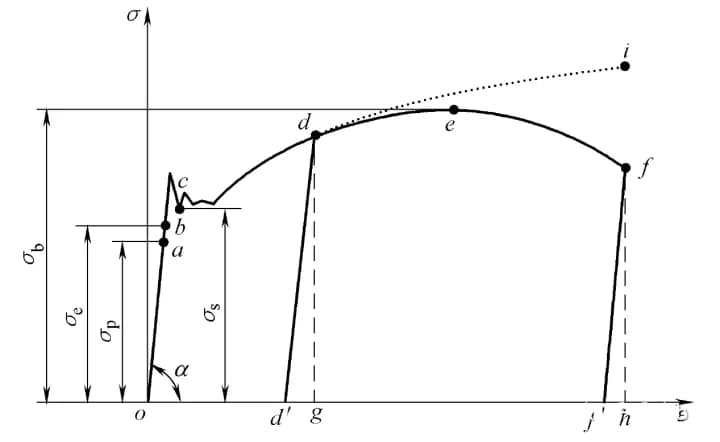
Het diagram van de spanning-rek (σ-ε) curve wordt getoond in Figuur 3.
In plaats van de axiale belasting F wordt de nominale spanning σ = F / A0 genomen en in plaats van de verlenging Δl wordt de engineering rek ε = Δl / l0 genomen.
De spanning-rek curve heeft nog steeds vier stadia. De betekenissen van elk karakteristiek punt zijn:
Stadium o naar a:
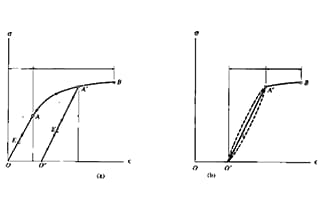
In het beginstadium van uitrekken (of comprimeren) zijn de spanning σ en de rek ε lineair gerelateerd tot punt a.
Op dit punt wordt de spanningswaarde die overeenkomt met punt a de proportionele limiet genoemd, voorgesteld door σp.
Het is de maximale limiet waar spanning en rek evenredig zijn.
Wanneer σ≤σp, geldt σ =Eε, ook bekend als de wet van Hooke, die aangeeft dat spanning en rek evenredig zijn.
Daarom is E =σ / ε = tanα, waarbij E bekend staat als de elasticiteitsmodulus of Young's modulus, met dezelfde eenheden als σ. Wanneer de spanning de proportionele grens overschrijdt om punt b te bereiken, wijkt de σ-ε relatie af van een rechte lijn.
Als de spanning op dit punt tot nul wordt ontladen, zal de rek ook verdwijnen (zodra de spanning punt b overschrijdt, kan een deel van de rek niet worden geëlimineerd na het ontladen).
De spanning gedefinieerd op punt b wordt de elasticiteitsgrens σe genoemd. σe is de uiterste grenswaarde voor alleen elastische vervorming van het materiaal.
Stadium b naar c:
Nadat de spanning de elasticiteitsgrens overschrijdt, treedt een fenomeen op waarbij de spanning niet of nauwelijks toeneemt en de rek snel toeneemt.
Dit fenomeen wordt buigen genoemd. Het punt waar het buigen begint komt overeen met de vloeigrens σs, ook wel de vloeigrens genoemd.
In het vloeistadium verandert de spanning niet terwijl de rek blijft toenemen, het materiaal lijkt zijn vermogen om vervorming te weerstaan te hebben verloren, wat resulteert in aanzienlijke plastische vervorming (als het op dit punt wordt ontladen, zal de rek niet volledig verdwijnen en zal er restvervorming zijn).
Daarom is σs een belangrijke index voor het meten van materiaalsterkte.
Wanneer een staal met een laag koolstofgehalte bezwijkt bij het oppervlaktepolijsten, zal het oppervlak strepen vertonen onder een hoek van 45° ten opzichte van de as, als gevolg van het relatieve glijden van het interne kristalrooster, bekend als sliplijnen.
Stadium c tot e:
Nadat het rekstadium is gepasseerd, moet het proefstuk verder worden belast om te blijven vervormen, het materiaal lijkt te zijn versterkt en het c-e stadium is het versterkende stadium.
Het hoogste punt (punt e) in de fase van rekversterking komt overeen met de sterktegrens σb. Het vertegenwoordigt de maximale spanning die het materiaal kan weerstaan.
Stadium e naar f:
Na het passeren van punt e, d.w.z. nadat de spanning de sterktegrens bereikt, ondergaat het proefstuk plaatselijk een ernstige krimp, die bekend staat als halsvorming.
Dan ontstaan er scheuren in het proefstuk, de nominale spanning σ neemt af en het proefstuk breekt op punt f.
De vloeigrens (σs) en de treksterkte (σb) zijn belangrijke indicatoren van de sterkte van materialen met een goede plasticiteit (zoals staal met een laag koolstofgehalte).
Er moet worden opgemerkt dat de nominale spanning wordt gebruikt en dat de vermindering in dwarsdoorsnede die gepaard gaat met de rekvervorming niet wordt beschouwd.
De treksterkte (σb) is alleen de nominale maximale spanning die het materiaal kan weerstaan, niet de werkelijke maximale spanning in het materiaal.
Als de werkelijke oppervlakte van het proefstuk op het moment van breuk wordt gebruikt om te meten, is de werkelijke maximale spanning de spanningswaarde die overeenkomt met punt i op de lijn d-i segment in de figuur.
In de engineeringpraktijk wordt de treksterkte (σb) omwille van de eenvoud, bruikbaarheid en veiligheid nog steeds gebruikt om de maximale spanning weer te geven die het materiaal kan weerstaan.
Bij het simuleren van het niet-lineaire mechanische gedrag van materialen met een computer moet echter de echte spanning-rek curve gebruikt worden.
Voor metalen zonder significant rekverschijnsel kan hun treksterkte onder voorgeschreven niet-proportionele verlenging of resttrek worden gemeten.
Voor metalen met een significant vloeiverschijnsel kunnen hun vloeigrens, bovenste vloeigrens en onderste vloeigrens gemeten worden.
Er zijn twee methoden om de bovenste en onderste vloeigrens te meten: de grafische methode en de aanwijsmethode.
Grafische methode
Tijdens het experiment wordt een kracht-kaakverplaatsingsgrafiek getekend met behulp van een automatisch registratieapparaat.
De verhouding tussen de krachtas en de spanning die elke millimeter vertegenwoordigt, moet minder dan 10 N/mm zijn.2en de curve moet ten minste tot het einde van de opbrengstfase worden getrokken.
Op de kromme wordt de constante kracht Fe tijdens het buigen, de maximale kracht Feh voor de eerste krachtafname tijdens het buigen of de minimale kracht FeL voor het initiële momentane effect bepaald.
De vloeigrens, bovenste vloeigrens en onderste vloeigrens kunnen berekend worden met de volgende formules:
Formule voor het berekenen van de vloeigrens: Re = Fe/So; Fe is de constante kracht tijdens het buigen.
Formule voor berekening van de bovenste rekgrens: Reh = Feh/So; Feh is de maximale kracht vóór de eerste afname van de kracht tijdens de rekfase.
Formule voor het berekenen van de lagere vloeigrens: ReL = FeL/So; FeL is de minimale kracht vóór het initiële momentane effect.
Wijzermethode
Tijdens het experiment, wanneer de wijzer van de krachtmeter stopt met draaien bij de constante kracht of de maximale kracht voor de eerste terugkeer of de minimale kracht voor het initiële momentane effect, komen deze respectievelijk overeen met de vloeigrens, de bovenste vloeigrens en de onderste vloeigrens.
De interne factoren die de vloeigrens beïnvloeden zijn: binding, microstructuur, structuur en atomaire aard.
Een vergelijking van de opbrengst sterkte van metalen met keramiek en polymeren laat zien dat het effect van binding fundamenteel is.
In termen van de invloed van de microstructuur zijn er vier versterkingsmechanismen die de vloeigrens van metaalmaterialen beïnvloeden:
(1) versterking van de vaste oplossing;
(2) spanningsuitharding;
(3) neerslagversterking en dispersieversterking;
(4) korrelgrensversterking en subkorrelversterking. Precipitatieversterking en fijnkorrelversterking zijn de meest gebruikte middelen om de vloeigrens van industriële legeringen te verbeteren.
Van deze versterkingsmechanismen verhogen de eerste drie mechanismen de sterkte van het materiaal terwijl ze ook de plasticiteit verminderen.
Alleen het verfijnen van de korrelgrootte en subkorrel kan de sterkte en plasticiteit van het materiaal verhogen.
De externe factoren die de vloeigrens beïnvloeden zijn: temperatuur, reksnelheid en spanningstoestand.
Als de temperatuur afneemt en de reksnelheid toeneemt, neemt de vloeigrens van het materiaal toe, vooral de lichaamsgecentreerde kubieke metalen zijn bijzonder gevoelig voor temperatuur en reksnelheid, wat leidt tot brosse breuk van staal bij lage temperatuur.
De invloed van de spanningstoestand is ook belangrijk. Hoewel de vloeigrens de inherente prestatie van een materiaal weergeeft, verschilt de vloeigrenswaarde ook afhankelijk van de spanningstoestand.
De vloeigrens van een materiaal waarnaar gewoonlijk wordt verwezen, is over het algemeen de vloeigrens onder eenassige spanning.
| Staalsoort | Mechanische eigenschap | Chemische samenstelling | ||||||||
| treksterkte | treksterkte | rek | C | Si | Mn | S | P | |||
| MPa | kg/mm2 | MPa | kg/mm2 | mm | Minder dan of gelijk aan. | Minder dan of gelijk aan. | Minder dan of gelijk aan. | |||
| Q215A Q215B | 215 | 22 | 335-410 | 3442 | 31 | 0.09-0.15 | 0.03 | 0.25-0.55 | 0.050 0.045 | 0.045 |
| Q235A Q235B Q235C Q235D | 235 | 24 | 375-460 | 38-47 | 26 | 0.14-0.22 0.12-0.20 ≤0.18 ≤0.17 | 0.30 | 0.30-0.65 0.30-0.70 0.35-0.80 0.35-0.80 | 0.5 0.45 0.40 0.035 | 0.045 0.045 0.040 0.035 |
| Mn (Q345B) | 345 | 35 | 510-600. | 51.60 | 22 | 0.12-0.200 | .20-0.55 | 1.2-1.6 | 0.045 | 0.045 |
Het testen van de vloeigrens is een belangrijke indicator voor de sterkte-eigenschappen van materialen en een kritische indicator voor de prestaties van materialen.
Het wordt vaak gebruikt om de sterkte van het materiaaloppervlak en de plastische prestaties te evalueren.
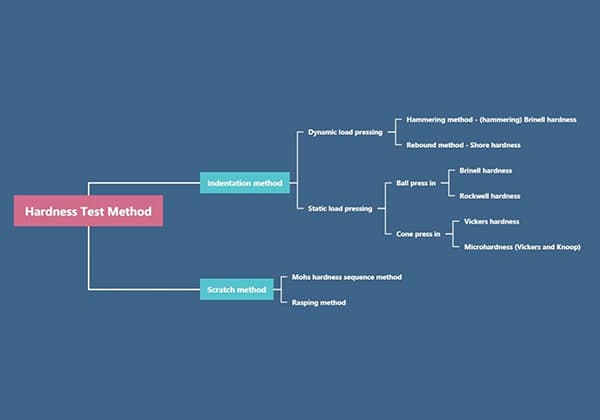
Testmethoden voor de vloeigrens worden over het algemeen verdeeld in twee types: mechanisch en niet-mechanisch.
Mechanisch testen van de vloeigrens:
Deze methode omvat over het algemeen driepuntsbuigen, de trekbankmethode en de compressiemethode. Het monster wordt tussen twee steunen geplaatst en er wordt een constante kracht uitgeoefend met een mechanisch apparaat om de vloeigrens te bepalen.
Niet-mechanisch testen van de vloeigrens:
Deze methode omvat over het algemeen trek-, compressie- en torsiemethoden. Het proefstuk wordt op het testinstrument geplaatst en er wordt een constante kracht uitgeoefend met behulp van een hefboom of computerbesturing om de vloeigrens te bepalen.
Om de nauwkeurigheid en precisie van vloeigrens testen te verbeteren, is het over het algemeen nodig om meerdere testen onder de nodige omstandigheden uit te voeren en de gemiddelde waarde te nemen.
In alle experimenten moet de behandeling van het proefstuk gestandaardiseerd en volledig zijn en moet het proefstuk constant gehouden worden onder de toegepaste kracht. De uiteindelijk verkregen vloeigrens is de maximale sterkte waarbij het materiaal kan buigen onder de toegepaste belasting.
Door het bestuderen van dit artikel hebben we geleerd wat vloeigrens is, de basisprincipes van spanning en rek, methoden om de vloeigrens te bepalen, factoren die de vloeigrens beïnvloeden en toepassingen van vloeigrens.
We hopen dat deze informatie nuttig is voor iedereen.
Als er vragen zijn, laat het ons dan weten in het commentaargedeelte.
Als oprichter van MachineMFG heb ik meer dan tien jaar van mijn carrière gewijd aan de metaalbewerkingsindustrie. Door mijn uitgebreide ervaring ben ik een expert geworden op het gebied van plaatbewerking, verspaning, werktuigbouwkunde en gereedschapsmachines voor metalen. Ik denk, lees en schrijf voortdurend over deze onderwerpen en streef er voortdurend naar om voorop te blijven lopen in mijn vakgebied. Laat mijn kennis en expertise een aanwinst zijn voor uw bedrijf.
NL 
EN 
AR 
DE 
ES 
FR 
IT 
JA 
PT 
PT_BR 
RU 
KO