Calculadora de subsídios de dobragem (online e gratuita)

Compreender a dobragem

A tolerância de dobragem é um conceito fundamental no fabrico de chapas metálicas, essencial para obter dimensões exactas em peças metálicas dobradas. É responsável pelo alongamento do material que ocorre durante o processo de dobragem, assegurando que as dimensões finais da peça correspondem às especificações do projeto.

Definição de subsídio de dobragem

A tolerância de dobragem refere-se ao comprimento do eixo neutro desde o início até ao fim da dobragem. O eixo neutro é uma linha imaginária dentro do material que não sofre compressão ou alongamento durante a dobragem. Este cálculo é crucial para determinar a disposição do padrão plano de uma peça de chapa metálica, uma vez que considera a deformação do material quando dobrado.

Importância na conceção de chapas metálicas

O cálculo exato da tolerância de dobragem é vital por várias razões. Em primeiro lugar, garante que as dimensões finais da peça dobrada correspondem às especificações do projeto. Além disso, ajuda a minimizar o desperdício de material ao prever com exatidão a quantidade de material necessária. Esta redução do desperdício conduz a poupanças de custos no processo de fabrico, reduzindo o risco de erros e retrabalho.

Factores que afectam a margem de curvatura

Vários factores influenciam a tolerância à curvatura. A espessura do material (T) desempenha um papel significativo, uma vez que os materiais mais espessos têm caraterísticas de dobragem diferentes dos materiais mais finos. O ângulo de curvatura (θ), normalmente medido como ângulo complementar, afecta a extensão do material. O raio interior (r) da curvatura no interior do material também afecta o cálculo. Por último, o fator K (K), uma constante específica do material que representa o rácio entre a espessura do material e o eixo neutro, é crucial.

Fórmula de dobragem

A margem de curvatura pode ser calculada através da seguinte fórmula:

Onde:

• ( BA ) é a margem de curvatura.
• ( θ ) é o ângulo de curvatura em graus.
• ( π/180 ) é um fator de conversão para converter graus em radianos.
• ( r ) é o raio interior.
• ( K ) é o fator K.
• ( T ) é a espessura do material.

Exemplo prático

Considere uma peça de chapa metálica com as seguintes propriedades:

• Ângulo de curvatura (( θ )) = 90°
• Raio interior (( r )) = 5 mm
• Espessura do material (( T )) = 2 mm
• Fator K (( K )) = 0,33

Utilizando a fórmula de dobragem:

Este cálculo fornece a margem de curvatura necessária para desenvolver com precisão o padrão plano da peça de chapa metálica.

I. Calculadora de dobras

Para novos travão de prensa Para os operadores que podem não estar familiarizados com os meandros do cálculo da tolerância de dobra, uma calculadora de tolerância de dobra pode ser uma ferramenta inestimável. Esta calculadora simplifica o processo, garantindo resultados exactos e tornando o trabalho diário mais eficiente.

As calculadoras online de tolerância de dobragem simplificam o processo, permitindo aos utilizadores introduzir parâmetros como a espessura do material, o ângulo de dobragem, o raio interior e o fator K. Estas calculadoras calculam então a tolerância de curvatura e, por vezes, a dedução de curvatura, garantindo um fabrico de chapa metálica preciso. Ao utilizar estas ferramentas, os fabricantes podem poupar tempo e reduzir o risco de erros nos seus cálculos.

Parâmetros necessários para o cálculo

Para utilizar eficazmente a calculadora da margem de curvatura, os operadores devem introduzir os parâmetros seguintes:

1. Espessura do material: A espessura do material influencia o raio de curvatura e a margem de curvatura global.
2. Raio interior: O raio da curvatura na superfície interior do material.
3. Fator K: Uma relação que ajuda a determinar a localização do eixo neutro durante a flexão.
4. Ângulo de curvatura: O ângulo em que o material é dobrado.

Calculadora relacionada:

• Calculadora do Fator K
• Calculadora do fator Y
• Calculadora de dedução de dobras

Ler mais:

• Como calcular a margem de curvatura, a dedução de curvatura e o fator K?

II. O que é Tolerância de dobragem?

A tolerância de dobragem é o comprimento adicional de material necessário quando se dobra uma chapa metálica para atingir as dimensões finais pretendidas após a conformação. Compensa o estiramento e a compressão que ocorrem no material durante o processo de dobragem. A margem de dobragem varia com base em vários factores:

1. Propriedades do material: Diferentes materiais têm diferentes elasticidades e plasticidades, que afectam o quanto o material se estica ou comprime durante a flexão.
2. Espessura da chapa: As chapas mais grossas requerem geralmente uma margem de dobragem maior do que as chapas mais finas do mesmo material.
3. Método de dobragem e ferramentas: O tipo de processo de dobragem (por exemplo, dobragem por ar, bottoming, cunhagem) e o design da matriz de dobragem podem influenciar a tolerância de dobragem.
4. Raio de curvatura interior: Um raio de curvatura interior mais apertado requer normalmente uma margem de curvatura mais pequena do que um raio maior.

Os valores das tolerâncias de dobragem são normalmente determinados através de uma combinação de dados empíricos, cálculos matemáticos e experiência prática. Os projectistas e engenheiros de chapa metálica experientes desenvolveram tabelas e fórmulas de tolerância de dobragem ao longo de anos de testes e verificações repetidos.

Utilizando a fórmula de dobragem adequada ou consultando gráficos de dobragem fiáveis, os designers podem calcular com precisão as dimensões do padrão plano de uma peça de chapa metálica que produzirá as dimensões de dobragem finais desejadas. Isto é crucial para criar padrões planos exactos e garantir que a peça dobrada se adapta e funciona como pretendido.

III. Fórmula da dobragem

Os cálculos da tolerância à dobragem e da dedução da dobragem são métodos essenciais utilizados para determinar o comprimento das matérias-primas de chapa metálica na sua forma plana, assegurando que o tamanho pretendido da peça dobrada é alcançado. A compreensão destes cálculos é crucial para a precisão no fabrico de chapas metálicas.

Método de cálculo da margem de curvatura:

A margem de dobragem (BA) é a quantidade de material que é adicionada ao comprimento total da chapa plana para ter em conta o material que será utilizado na dobragem. 

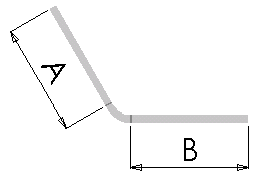
A equação seguinte é utilizada para determinar o comprimento total de aplanamento quando é utilizado o valor da tolerância de curvatura:

L_t = A + B + BA

Onde:

• 𝐿_𝑡 é o comprimento total do plano.
• 𝐴 e 𝐵 são os comprimentos das duas secções rectas da chapa metálica antes da dobra (como mostra a figura).
• 𝐵𝐴 é o valor da tolerância à flexão.

Método de cálculo da dedução de dobras:

A dedução de dobragem (BD) é a quantidade de material que é subtraída do comprimento total da chapa plana para ter em conta o material que será utilizado na dobragem. 

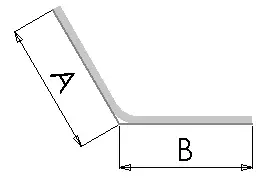
A equação seguinte é utilizada para determinar o comprimento total de aplanamento quando se utiliza o valor de dedução da curvatura:

L_t = A + B - BD

Onde:

• 𝐿_𝑡 é o comprimento total do plano.
• 𝐴 e 𝐵 são os comprimentos das duas secções rectas da chapa metálica antes da dobra (como mostra a figura).
• 𝐵𝐷 é o valor de dedução da curvatura.

Outros métodos de cálculo

Para além dos métodos de dedução de dobragem e de dedução de dobragem, podem ser utilizadas outras técnicas para determinar o comprimento plano de matérias-primas de chapa metálica. Estas incluem:

• Gráfico de tolerância à flexão: Uma tabela pré-calculada que fornece valores de tolerância de curvatura para vários materiais e ângulos de curvatura.
• Fator K: Rácio que representa a localização do eixo neutro em relação à espessura do material. É utilizado em cálculos de flexão mais precisos.
• Cálculos de flexão: Estas envolvem fórmulas e considerações mais complexas, como as propriedades do material, o raio de curvatura e a espessura, para obter resultados exactos.

IV. Tabela de tolerâncias de dobragem

1. Tabela de tolerância à flexão para SPCC (aço macio)

2. Tabela de tolerância à flexão para SUS (aço inoxidável)

3. Tabela de tolerâncias de curvatura para SPHC (aço inoxidável)

4. Tabela de tolerâncias de curvatura para a CCEE (chapa de aço galvanizado)

5. Tabela de tolerâncias de dobragem para chapas de alumínio

V. Importância do fator K

Definição e papel do fator K

O fator K é um coeficiente crucial no fabrico de chapas metálicas, representando a posição relativa do eixo neutro dentro da espessura do material. O eixo neutro é o plano imaginário dentro do material onde não ocorre compressão ou tensão durante o processo de flexão. O fator K é calculado como a relação entre a distância da superfície interior ao eixo neutro e a espessura total do material. A compreensão do fator K é essencial para cálculos precisos da tolerância de dobragem, garantindo a precisão das dimensões finais das peças dobradas.

Influência na capacidade de dobragem

O fator K influencia diretamente a tolerância de dobragem, que é o comprimento adicional de material necessário para acomodar a dobragem. A fórmula da margem de curvatura, que normalmente inclui o ângulo de curvatura, o raio interior, a espessura do material e o fator K, é a seguinte

em que ( BA ) é a margem de curvatura, ( θ ) é o ângulo de curvatura em radianos, ( r ) é o raio interior, ( K ) é o fator K e ( T ) é a espessura do material. Esta fórmula realça a importância do fator K para garantir que a tolerância de curvatura é calculada com precisão, o que é fundamental para obter dimensões precisas da peça e reduzir o desperdício de material.

Dependência de materiais e processos

O fator K não é um valor constante e varia em função de vários factores, incluindo as propriedades do material, o método de dobragem, o raio de dobragem e o ângulo de dobragem. Diferentes materiais e condições de dobragem resultarão em diferentes valores do fator K, que normalmente variam entre 0,3 e 0,5. Por exemplo, um material com elevada ductilidade pode ter um fator K diferente em comparação com um material mais frágil, influenciando a tolerância de dobragem e, consequentemente, as dimensões finais da peça.

VI. Aplicação prática: Guia passo a passo

Passo 1: Reunir os parâmetros necessários

Para calcular com exatidão a margem de curvatura e a dedução de curvatura, comece por recolher os seguintes parâmetros:

• Espessura do material (T): Medir a espessura da chapa metálica, normalmente em milímetros (mm) ou polegadas (in).
• Ângulo de curvatura (θ): Determine o ângulo em que a chapa metálica será dobrada. Os ângulos mais comuns são 90°, 120°, etc.
• Raio interior (IR): Medir o raio da curvatura no interior do material.
• Fator K (K): O fator K representa a relação entre o eixo neutro do material e a sua espessura e é essencial para determinar a quantidade de material necessária para uma dobra. Normalmente, varia entre 0,3 e 0,5, dependendo das propriedades e da espessura do material.

Passo 2: Calcular a tolerância de curvatura (BA)

A margem de curvatura representa o comprimento adicional de material necessário para acomodar a curvatura. Utilize a fórmula da margem de curvatura para determinar este valor:

Exemplo de cálculo:

• Material: Aço macio
• Espessura (T): 0,125 polegadas
• Raio interior (IR): 0,250 polegadas
• Ângulo de curvatura (θ): 90 graus
• Fator K (K): 0.42

1. Converter o ângulo de curvatura em radianos:

2. Aplicar a fórmula da tolerância de curvatura:

Passo 3: Calcular o recuo exterior (OSSB)

Em seguida, determinar o recuo exterior, que é importante para o cálculo da dedução da dobra. A fórmula para OSSB é:

Exemplo de cálculo:

• Ângulo de curvatura (θ): 90 graus
• Espessura do material (T): 0,125 polegadas
• Raio interior (IR): 0,250 polegadas

Converter o ângulo de curvatura em radianos:

Aplicar a fórmula do recuo exterior:

Etapa 4: Calcular a dedução de curvatura (BD)

Por fim, utilize o recuo exterior e a margem de curvatura para determinar a dedução de curvatura, que é crucial para obter dimensões exactas no fabrico de chapas metálicas:

Exemplo de cálculo:

• Recuo exterior (OSSB): 0,375 polegadas
• Tolerância de curvatura (BA): 0,475 polegadas

Aplicar a fórmula de dedução de dobra:

Considerações práticas

Compreender o significado de cada parâmetro é vital para operações de dobragem bem sucedidas. O fator K, por exemplo, influencia a quantidade de material necessária para a dobragem, enquanto que a margem de dobragem assegura que o material se encaixará corretamente após a dobragem. Além disso, é essencial ter em conta o retorno elástico, um fenómeno em que o metal regressa ligeiramente à sua forma original após a dobragem, o que pode exigir uma dobragem excessiva do material.

Seguindo estes passos e considerando cuidadosamente cada parâmetro, é possível calcular com exatidão a margem de curvatura e a dedução de curvatura necessárias para o fabrico preciso de chapas metálicas.