Já alguma vez se interrogou sobre como calcular com precisão a margem de curvatura para os seus projectos de fabrico de metais? Nesta publicação do blogue, vamos explorar o fascinante mundo das fórmulas e cálculos da tolerância à flexão. Como engenheiro mecânico experiente, guiá-lo-ei através dos conceitos-chave e fornecer-lhe-ei informações práticas para o ajudar a dominar este aspeto crucial do design de chapas metálicas. Prepare-se para mergulhar e desvendar os segredos da criação de dobras precisas e eficientes nos seus projectos!
A tolerância de dobragem é um conceito crítico no domínio do fabrico de chapas metálicas, particularmente quando se trabalha com operações de dobragem. Refere-se ao comprimento adicional de material necessário para acomodar a dobra na chapa metálica. Compreender e calcular com exatidão a tolerância de dobragem é essencial para garantir que as dimensões finais da peça dobrada cumprem as especificações do projeto.
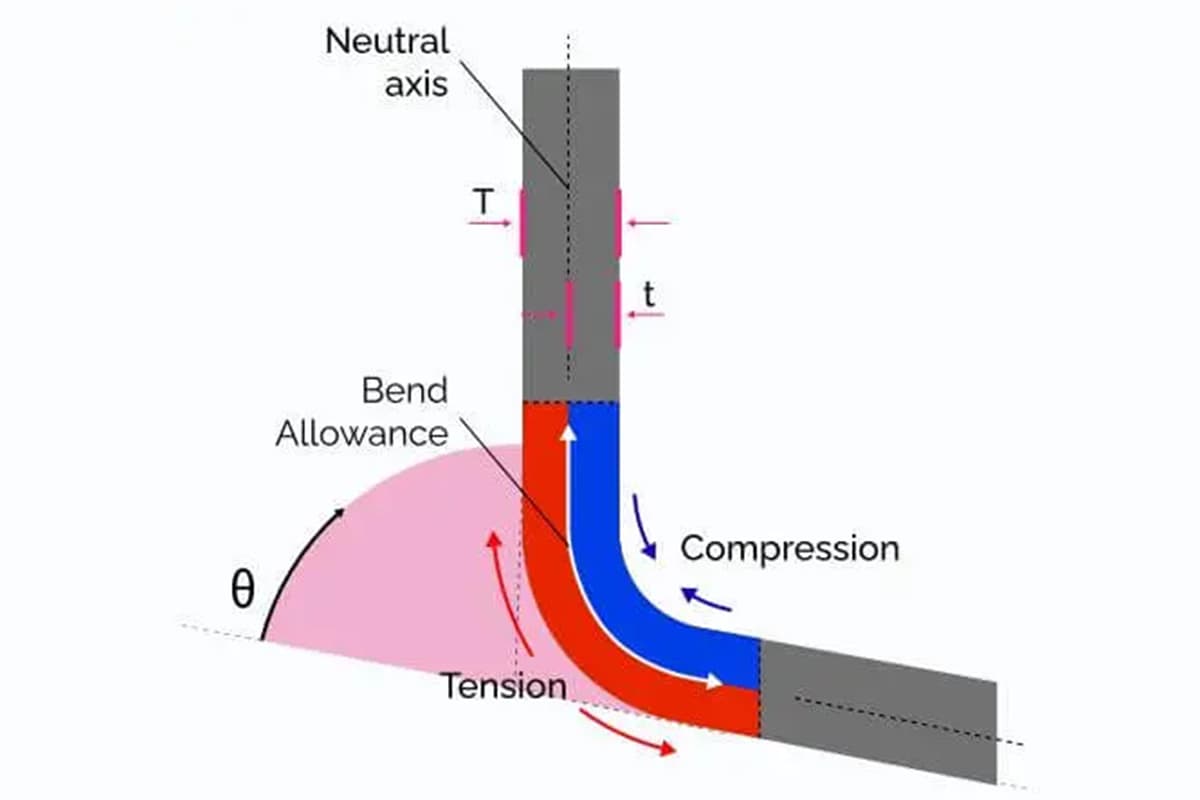
Os cálculos exactos da tolerância de dobragem são vitais no processo de fabrico. Quando uma folha de metal plana é dobrada, o material no exterior da dobra estica-se, enquanto o material no interior se comprime. Sem ter em conta esta deformação, o produto final não corresponderia ao design pretendido, levando a imprecisões e potenciais falhas. A tolerância de dobragem ajuda os fabricantes a ajustar as dimensões do padrão plano, assegurando que a peça dobrada cumpre requisitos precisos.
Vários parâmetros críticos influenciam os cálculos da tolerância à flexão:
O conceito de tolerância à flexão é a seguinte: quando uma folha de metal é dobrada, tem três dimensões - duas dimensões exteriores (L1 e L2) e uma dimensão de espessura (T).
É importante notar que a soma de L1 e L2 é maior do que o comprimento desdobrado (L), e a diferença entre os dois é conhecida como a tolerância à flexão (K).
Assim, o comprimento desdobrado de uma curva pode ser calculado como L = L1 + L2 - K.
Leitura relacionada:
Como é que a fórmula para tolerância de curvatura criado? E como é que se calcula tolerância de curvatura?
A tolerância de dobragem depende do raio interior formado. A abertura inferior da matriz V determina o raio interior (I.R.) de uma peça formada. O raio interior para aço macio é 5/32 x abertura inferior da matriz V (W) quando o raio do punção é inferior a 5/32 x W.
Se I.R.< Espessura do material (t)
Se I.R.> 2 x Espessura do material (t)
Em que A= (180 - Ângulo de inclusão da curvatura)
Se o raio interior for igual a t ou 2t, ou entre t e 2t, a margem de curvatura é calculada por interpolação dos valores da margem de curvatura das duas fórmulas acima referidas.
Além disso, para calcular esta margem de curvatura, pode também utilizar a seguinte fórmula
Esta fórmula tem em conta as diferentes geometrias e propriedades das peças a formar.
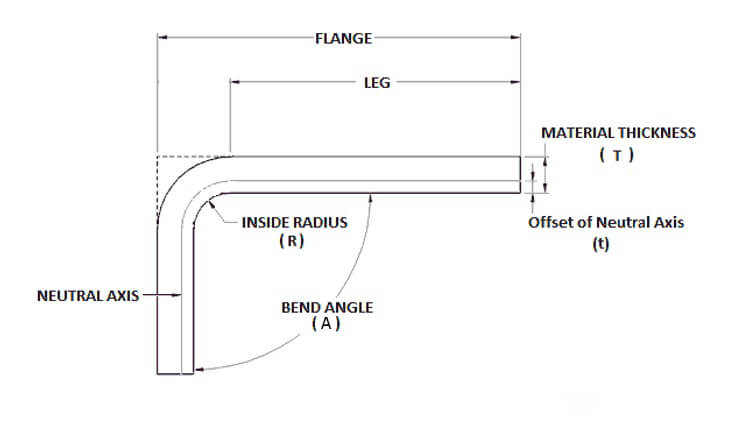
A espessura do material (T), o ângulo de flexão (A), o ângulo interno raio de curvatura (R), e o fator K do material a ser dobrado são os factores mais críticos neste cálculo.
Como se pode ver pela fórmula acima, o cálculo da margem de curvatura é um processo simples.
Pode determinar a tolerância à flexão substituindo os valores acima mencionados na fórmula.
Quando o ângulo de flexão é de 90°, a fórmula da tolerância à flexão pode ser simplificada do seguinte modo
Nota: O fator K para a maioria dos materiais e espessuras padrão situa-se normalmente entre 0 e 0,5.
O valor do fator K pode ser calculado com precisão da seguinte forma Calculadora do fator K:
A fórmula da tolerância de dobragem (BA) é essencial para calcular o comprimento de material necessário para formar uma dobragem. Esta fórmula geral é amplamente aplicável em diferentes materiais e métodos de dobragem:
Onde:
O fator K é crucial, uma vez que indica a posição do eixo neutro, que não muda de comprimento durante a flexão. Normalmente, o fator K situa-se entre 0,3 e 0,5 e varia consoante o tipo de material, a espessura, o raio e o método de dobragem.
Diferentes materiais têm propriedades únicas que necessitam de ajustes aos cálculos de tolerância de dobragem. Estes ajustamentos garantem a exatidão, particularmente nas curvas de 90°:
Para materiais mais macios, como o latão macio ou o cobre, a margem de curvatura é calculada da seguinte forma:
BA = (0,55 × T) + (1,57 × R
Este ajustamento tem em conta a ductilidade do material e a sua menor resistência à deformação.
Para cobre semi-duro ou latão, aço macio e alumínio, a tolerância de dobra é:
BA = (0,64 x T) + (1,57 × R)
Estes materiais têm uma dureza moderada, exigindo uma tolerância ligeiramente superior à dos materiais mais macios.
Para materiais mais duros, como bronze, cobre duro, aço laminado a frio e aço para molas, a fórmula é:
BA = (0,71 x T) + (1,57 × R)
Estes materiais são mais resistentes à flexão, o que exige uma tolerância mais elevada.
Para determinar o comprimento plano total da peça de chapa metálica, a margem de curvatura é adicionada aos comprimentos das partes planas:
Comprimento plano = Comprimento da perna 1 + BA + Comprimento da perna 2
Esta abordagem garante que as dimensões finais da peça são exactas após a dobragem.
Considere uma dobra de 90° numa folha de alumínio com uma espessura de 2 mm e um raio de dobra interior de 5 mm. Utilizando a fórmula específica do material para cobre semi-duro, latão, aço macio e alumínio:
BA = (0,64 × 2) + (1,57 × 5)
BA = 1,28 + 7,85=9,13
Se a peça tiver duas secções planas de 50 mm cada, o comprimento total do plano será:
Comprimento plano = 50 + 9,13 + 50 = 109,13 mm
Para além da tolerância de curvatura, a dedução de curvatura (BD) e o recuo exterior (OSSB) são importantes para medições precisas:
Dedução de dobra (BD) = OSSB - BA
Onde:
Estas formulações e considerações são essenciais para calcular com precisão as tolerâncias de dobragem, assegurando que as peças de chapa metálica são fabricadas com as dimensões e o ajuste corretos.
A tolerância de dobragem é um fator crítico no processo de dobragem de chapa metálica, particularmente para materiais como o alumínio. É responsável pelo estiramento do material que ocorre durante a dobragem, garantindo dimensões finais precisas. Aqui, discutiremos a fórmula específica usada para chapas de alumínio e sua aplicação.
A tolerância à flexão para uma placa de alumínio pode ser calculada utilizando a seguinte fórmula:
𝐿=𝐿1+𝐿2-1.6𝑇
Onde:
O valor 1,6𝑇 é derivado empiricamente, o que significa que foi estabelecido através da experimentação prática e da experiência de produção. Este fator tem em conta o comportamento do material durante a flexão, garantindo que as dimensões finais são precisas.
É fundamental notar que esta fórmula é especificamente aplicável em determinadas condições:
Para determinar o tamanho expandido da placa de alumínio, siga estes passos:
Este cálculo dar-lhe-á o comprimento do padrão plano necessário antes de dobrar, assegurando que a peça dobrada final tem as dimensões correctas.
A calculadora de tolerância de dobra fornecida abaixo simplifica o processo de cálculo do valor da tolerância de dobra, que é crucial para a fabricação precisa de chapas metálicas. A tolerância de dobragem é o comprimento do eixo neutro entre as linhas de dobragem, o que ajuda a determinar o tamanho correto da peça em bruto para uma peça dobrada.
O ângulo de curvatura, denotado como θ, é um parâmetro crucial na fórmula da tolerância à curvatura. Representa o ângulo através do qual a chapa metálica é dobrada. O ângulo de curvatura é normalmente medido em graus, mas pode ser convertido em radianos utilizando a fórmula:
O raio interior, representado por r, é o raio da curva interior da dobragem. Este raio influencia diretamente a quantidade de alongamento e compressão que ocorre no material durante a dobragem. Um raio interior mais pequeno resulta numa deformação mais significativa, que deve ser tida em conta no cálculo da tolerância de dobragem.
A espessura do material, indicada como T, é a espessura da chapa metálica que está a ser dobrada. Os materiais mais espessos sofrem um alongamento e uma compressão mais pronunciados, afectando a tolerância global de dobragem. A medição exacta da espessura do material é essencial para cálculos precisos da tolerância de dobragem.
O fator K é um valor adimensional que representa a posição do eixo neutro relativamente à espessura do material. O eixo neutro é a linha teórica dentro do material que permanece inalterada em comprimento durante a flexão. O fator K varia com base nas propriedades do material e nos métodos de flexão, variando normalmente entre 0,3 e 0,5 para a maioria dos materiais. A fórmula para a posição do eixo neutro é:
Posição do eixo neutro = K × T
O eixo neutro é a linha imaginária dentro do material que permanece inalterada em comprimento durante a dobragem. Compreender a sua posição é crucial para calcular a tolerância de dobragem correta.
A margem de curvatura, representada por BA, é o comprimento do eixo neutro necessário para formar uma curvatura. É calculado através da fórmula:
Esta fórmula utiliza o ângulo de curvatura, o raio interior, a espessura do material e o fator K para garantir cálculos precisos da tolerância de curvatura.
A tabela de tolerância de dobragem é um recurso essencial para os profissionais que trabalham com o fabrico de chapas metálicas. Fornece uma lista abrangente de parâmetros-chave, como a espessura do material, o raio de curvatura, o ângulo de curvatura, a tolerância de curvatura e os valores de dedução de curvatura para materiais comuns. Esta informação é crucial para calcular com exatidão o comprimento de desenvolvimento de uma peça de chapa metálica após a dobragem.
Ler mais:
| TV | Ângulo | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Tamanho mais pequeno |
| V4 | 90 | 0.9 | 1.4 | 2.8 | ||||||||||
| V4 | 120 | 0.7 | ||||||||||||
| V4 | 150 | 0.2 | ||||||||||||
| V6 | 90 | 1.5 | 1.7 | 2.15 | 4.5 | |||||||||
| V6 | 120 | 0.7 | 0.86 | 1 | ||||||||||
| V6 | 150 | 0.2 | 0.3 | 0.4 | ||||||||||
| V7 | 90 | 1.6 | 1.8 | 2.1 | 2.4 | 5 | ||||||||
| V7 | 120 | 0.8 | 0.9 | 1 | ||||||||||
| V7 | 150 | 0.3 | 0.3 | 0.3 | ||||||||||
| V8 | 90 | 1.6 | 1.9 | 2.2 | 2.5 | 5.5 | ||||||||
| V8 | 30 | 0.3 | 0.34 | 0.4 | 0.5 | |||||||||
| V8 | 45 | 0.6 | 0.7 | 0.8 | 1 | |||||||||
| V8 | 60 | 1 | 1.1 | 1.3 | 1.5 | |||||||||
| V8 | 120 | 0.8 | 0.9 | 1.1 | 1.3 | |||||||||
| V8 | 150 | 0.3 | 0.3 | 0.2 | 0.5 | |||||||||
| V10 | 90 | 2.7 | 3.2 | 7 | ||||||||||
| V10 | 120 | 1.3 | 1.6 | |||||||||||
| V10 | 150 | 0.5 | 0.5 | |||||||||||
| V12 | 90 | 2.8 | 3.65 | 4.5 | 8.5 | |||||||||
| V12 | 30 | 0.5 | 0.6 | 0.7 | ||||||||||
| V12 | 45 | 1 | 1.3 | 1.5 | ||||||||||
| V12 | 60 | 1.7 | 2 | 2.4 | ||||||||||
| V12 | 120 | 1.4 | 1.7 | 2 | ||||||||||
| V12 | 150 | 0.5 | 0.6 | 0.7 | ||||||||||
| V14 | 90 | 4.3 | 10 | |||||||||||
| V14 | 120 | 2.1 | ||||||||||||
| V14 | 150 | 0.7 | ||||||||||||
| V16 | 90 | 4.5 | 5 | 11 | ||||||||||
| V16 | 120 | 2.2 | ||||||||||||
| V16 | 150 | 0.8 | ||||||||||||
| V18 | 90 | 4.6 | 13 | |||||||||||
| V18 | 120 | 2.3 | ||||||||||||
| V18 | 150 | 0.8 | ||||||||||||
| V20 | 90 | 4.8 | 5.1 | 6.6 | 14 | |||||||||
| V20 | 120 | 2.3 | 3.3 | |||||||||||
| V20 | 150 | 0.8 | 1.1 | |||||||||||
| V25 | 90 | 5.7 | 6.4 | 7 | 17.5 | |||||||||
| V25 | 120 | 2.8 | 3.1 | 3.4 | ||||||||||
| V25 | 150 | 1 | 1 | 1.2 | ||||||||||
| V32 | 90 | 7.5 | 8.2 | 22 | ||||||||||
| V32 | 120 | 4 | ||||||||||||
| V32 | 150 | 1.4 | ||||||||||||
| V40 | 90 | 8.7 | 9.4 | 28 | ||||||||||
| V40 | 120 | 4.3 | 4.6 | |||||||||||
| V40 | 150 | 1.5 | 1.6 |
| TV | Ângulo | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Tamanho mais pequeno |
| V4 | 1.4 | 2.8 | ||||||||||||
| V6 | 1.6 | 4.5 | ||||||||||||
| V7 | 1.6 | 1.8 | 5 | |||||||||||
| V8 | 1.8 | 2.4 | 3.1 | 5.5 | ||||||||||
| V10 | 2.4 | 3.2 | 7 | |||||||||||
| V12 | 2.4 | 3.2 | 8.5 | |||||||||||
| V14 | 3.2 | 10 | ||||||||||||
| V16 | 3.2 | 4 | 4.8 | 11 | ||||||||||
| V18 | 4.8 | 13 | ||||||||||||
| V20 | 4.8 | 14 | ||||||||||||
| V25 | 4.8 | 5.4 | 6 | 17.5 | ||||||||||
| V32 | 6.3 | 6.9 | 22 |
| Ângulo | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Tamanho mais pequeno |
| 90 | 3.6 | 5.2 | 6.8 | 8.4 | 28 | ||||||||
| 120 | |||||||||||||
| 150 |
| MATERIAL | SPCC | SUS | Al （LY12） | CCEE | ||||
|---|---|---|---|---|---|---|---|---|
| T | ΔT | ΔK | ΔT | ΔK | ΔT | ΔK | ΔT | ΔK |
| T=0.6 | 1.25 | 1.26 | ||||||
| T=0.8 | 0.18 | 1.42 | 0.15 | 1.45 | 0.09 | 1.51 | ||
| T=1.0 | 0.25 | 1.75 | 0.20 | 1.80 | 0.30 | 1.70 | 0.38 | 1.62 |
| T=1.2 | 0.45 | 1.95 | 0.25 | 2.15 | 0.50 | 1.90 | 0.43 | 1.97 |
| T=1.4 | 0.64 | 2.16 | ||||||
| T=1.5 | 0.64 | 2.36 | 0.50 | 2.50 | 0.70 | 2.30 | ||
| T=1.6 | 0.69 | 2.51 | ||||||
| T=1.8 | 0.65 | 3.00 | ||||||
| T=1.9 | 0.60 | 3.20 | ||||||
| T=2.0 | 0.65 | 3.35 | 0.50 | 3.50 | 0.97 | 3.03 | 0.81 | 3.19 |
| T=2.5 | 0.80 | 4.20 | 0.85 | 4.15 | 1.38 | 3.62 | ||
| T=3.0 | 1.00 | 5.00 | 5.20 | 1.40 | 4.60 | |||
| T=3.2 | 1.29 | 5.11 | ||||||
| T=4.0 | 1.20 | 6.80 | 1.00 | 7.00 | ||||
| T=5.0 | 2.20 | 7.80 | 2.20 | 7.80 | ||||
| T=6.0 | 2.20 | 9.80 | ||||||
Nota:
Uma tabela de tolerância de dobragem bem mantida é uma ferramenta vital na indústria de fabrico de chapas metálicas. Garante precisão e eficiência no processo de dobragem, conduzindo, em última análise, a produtos acabados de maior qualidade e mais exactos. Ao compreender e utilizar os valores fornecidos na tabela, os engenheiros e fabricantes podem obter resultados óptimos nos seus projectos.
No fabrico de chapas metálicas, alcançar precisão e exatidão é crucial para criar peças de alta qualidade. Um dos factores-chave que desempenham um papel significativo neste processo é o Fator K. Compreender o Fator K e a sua aplicação nos cálculos da tolerância de dobragem é essencial para que os fabricantes produzam peças que cumpram as especificações exactas e tenham um desempenho fiável em várias indústrias.
O fator K é um valor adimensional que representa a relação entre a distância do eixo neutro e a espessura do material. É crucial para cálculos exactos da tolerância de dobragem, que determinam a quantidade de material necessária para obter uma dobragem pretendida. O eixo neutro é uma linha imaginária dentro do material que não muda de comprimento durante a dobragem. Ao compreender o Fator K, os fabricantes podem prever como o material se comportará quando dobrado, assegurando processos de fabrico precisos e eficientes.
O fator K é calculado utilizando a fórmula:
Onde:
A utilização do fator K na fórmula da tolerância de dobragem ajuda a prever o alongamento e a compressão do material durante a dobragem. A fórmula da tolerância à flexão é:
Para ilustrar este facto, vejamos um exemplo simples. Suponhamos que temos uma peça de chapa metálica com uma espessura (T) de 2 mm, dobrada num ângulo de 90 graus (θ), com um raio interior (r) de 5 mm e um fator K (K) de 0,4.
1. Converter o ângulo de curvatura em radianos:
2. Aplicar os valores à fórmula da margem de curvatura:
Este cálculo mostra que são necessários aproximadamente 9,11 mm de material ao longo do eixo neutro para obter a curvatura desejada, demonstrando a importância de um fator K preciso.
O fator K tem um impacto direto na precisão dos cálculos da tolerância de dobragem. Um fator K preciso garante que as dimensões finais da peça dobrada correspondem às especificações do projeto, reduzindo o desperdício de material e a necessidade de retrabalho. Esta precisão é vital para as indústrias onde as dimensões exactas são cruciais para a montagem e funcionalidade dos componentes.
Diferentes materiais têm propriedades mecânicas únicas, o que resulta em valores de fator K variáveis. Os materiais mais macios, como o alumínio, têm normalmente um fator K mais baixo, enquanto os materiais mais duros, como o aço inoxidável, têm um fator K mais elevado. Compreender estas variações permite aos fabricantes selecionar valores de fator K adequados para diferentes materiais, assegurando cálculos precisos e processos de fabrico eficientes.
Seguem-se as respostas a algumas perguntas frequentes:
A fórmula de tolerância de dobragem é utilizada para calcular o comprimento do eixo neutro de uma dobragem em chapa metálica, o que é crucial para determinar o comprimento correto do padrão plano antes de o metal ser dobrado. Este cálculo assegura que as dimensões finais da peça dobrada correspondem às especificações do projeto.
A fórmula tem em conta vários parâmetros fundamentais:
A fórmula geral para a tolerância à flexão (BA) é a seguinte
Utilizando esta fórmula, é possível calcular o comprimento exato de material necessário para formar uma dobra, assegurando que o material não se estique excessivamente nem se comprima demasiado. Esta margem de curvatura calculada é depois adicionada aos comprimentos das pernas da peça para desenvolver um padrão plano exato, que é essencial para produzir peças com dimensões precisas.
A fórmula da tolerância de dobragem também está relacionada com a dedução de dobragem, que é o comprimento que tem de ser subtraído do comprimento total da chapa metálica para obter o padrão plano correto. A dedução de dobragem é calculada utilizando a tolerância de dobragem e o recuo exterior, assegurando que as dimensões finais da peça são exactas após a dobragem.
Por exemplo, se estiver a dobrar uma chapa de aço inoxidável de 2 mm de espessura num ângulo de 90° com um raio de curvatura interior de 3 mm e um fator K de 0,44, a margem de curvatura pode ser calculada da seguinte forma:
Esta margem de curvatura é depois utilizada para garantir que o padrão plano é corretamente desenvolvido, resultando numa peça que cumpre as especificações do projeto. Em resumo, a fórmula de tolerância de dobragem é essencial para o fabrico preciso de chapas metálicas, assegurando que as peças finais são produzidas com as dimensões corretas.
Para calcular a margem de curvatura em chapas metálicas, é necessário determinar vários parâmetros-chave: espessura do material (T), ângulo de curvatura (θ), raio interior (r) e o fator K (K). A margem de curvatura (BA) é calculada utilizando a fórmula:
Aqui está um processo passo a passo:
Utilizando esta fórmula, para os mesmos parâmetros:
Seguindo estes passos e utilizando a fórmula adequada, pode calcular com precisão a margem de curvatura para as suas peças de chapa metálica, assegurando um fabrico preciso.
O fator K é importante na fórmula da tolerância de dobragem por várias razões, cada uma delas realçando o seu significado no fabrico de chapas metálicas de precisão. Em primeiro lugar, representa a relação entre o eixo neutro e a espessura do material. Durante a dobragem, o eixo neutro desloca-se da sua localização original em 50% da espessura do material para a superfície interior da dobragem. Esta deslocação é crítica porque determina a quantidade de alongamento que ocorre no material. O fator K ajuda a calcular esta nova localização, o que é essencial para cálculos de dobragem precisos.
Em segundo lugar, o fator K é fundamental no cálculo da margem de curvatura, que é o comprimento da fibra neutra desde o início até ao fim do arco gerado pela curvatura. Este cálculo é necessário para determinar a dimensão plana da chapa metálica necessária para obter a forma de dobra desejada. A tolerância de dobragem é diretamente influenciada pelo fator K, uma vez que este é responsável pelo alongamento do material durante o processo de dobragem.
Além disso, a utilização do fator K permite cálculos precisos de deduções de dobragem, recuos exteriores e a disposição plana geral da peça. Esta precisão é vital porque garante que as dimensões finais da peça dobrada correspondem às especificações do projeto, evitando erros que poderiam surgir da utilização de valores genéricos ou imprecisos do fator K.
O fator K varia com base em vários parâmetros, incluindo o tipo de material, a espessura, o método de conformação, as ferramentas e o ângulo de dobragem. Esta variabilidade significa que o fator K deve ser adaptado às condições específicas do processo de quinagem. Ao considerar estes factores, o fator K ajuda a personalizar a fórmula de compensação de dobragem para obter resultados mais precisos.
Finalmente, um valor correto do fator K é essencial para evitar erros nas dimensões finais da folha dobrada. Valores incorrectos do fator K podem levar a imprecisões nas tolerâncias de dobragem, resultando em peças que não cumprem as especificações exigidas. Por conseguinte, determinar e utilizar com precisão o fator K é fundamental para produzir componentes de elevada qualidade.
Em suma, o fator K é importante porque permite o cálculo preciso das tolerâncias de dobragem, tem em conta o deslocamento do eixo neutro e considera os parâmetros específicos do material e do processo, todos eles essenciais para obter resultados precisos e fiáveis na dobragem de chapas metálicas.
A fórmula da tolerância de dobragem na dobragem de chapas metálicas inclui normalmente diversas variáveis-chave:
A margem de curvatura (BA) pode ser calculada através da fórmula:
ou
em que (0,017453) é (π/180) e (0,0078) é (π /180) x K) - fator.
Estas variáveis são essenciais para determinar com exatidão a tolerância de dobragem, que é crítica para o fabrico preciso de chapas metálicas.
Sim, a fórmula da tolerância de dobragem pode variar significativamente com base no tipo de material, bem como noutros factores como a espessura do material, o ângulo de dobragem e o processo de dobragem específico.
O fator K, um componente crítico da fórmula da tolerância à flexão, representa a deslocação do eixo neutro teórico durante a flexão e varia consoante o material. Por exemplo, o aço macio laminado a frio utiliza normalmente um fator K de cerca de 0,446, enquanto outros materiais, como o aço inoxidável e o alumínio, têm factores K diferentes devido às suas propriedades e comportamentos de flexão únicos.
A fórmula da tolerância de curvatura também incorpora a espessura do material e o ângulo de curvatura, que podem diferir consoante os materiais. Uma forma geral da fórmula da tolerância de curvatura é:
onde:
Diferentes materiais têm propriedades distintas, tais como elasticidade, resistência à tração e direção do grão, que influenciam o seu comportamento de dobragem. Por exemplo, o alumínio dobra-se mais facilmente do que o aço, exigindo ajustes no cálculo da tolerância de dobragem. Além disso, dobrar um metal ao longo da sua direção de grão pode exigir mais força e uma tolerância de dobragem diferente em comparação com a dobragem ao longo do grão.
A tendência do material para recuar após a flexão, conhecida como recuo elástico, também deve ser considerada. Isto implica uma ligeira sobreflexão do material para ter em conta a recuperação elástica, influenciada pelo tipo de material e pelas suas propriedades.
Em resumo, a fórmula da tolerância de dobragem deve ser adaptada ao material específico que está a ser utilizado, considerando as suas propriedades únicas, a espessura e o processo de dobragem envolvido.
Como fundador da MachineMFG, dediquei mais de uma década da minha carreira à indústria metalúrgica. A minha vasta experiência permitiu-me tornar-me um especialista nos domínios do fabrico de chapas metálicas, maquinagem, engenharia mecânica e máquinas-ferramentas para metais. Estou constantemente a pensar, a ler e a escrever sobre estes assuntos, esforçando-me constantemente por me manter na vanguarda da minha área. Deixe que os meus conhecimentos e experiência sejam uma mais-valia para a sua empresa.
PT 
EN 
AR 
DE 
ES 
FR 
ID 
IT 
JA 
NL 
PT_BR 
RU 
KO 
TR