Como é que os engenheiros garantem a resistência e a durabilidade das vigas sob várias cargas? Este artigo analisa os princípios da tensão de corte por flexão e as condições necessárias para manter a resistência da viga. Aborda a distribuição de tensões em diferentes secções de vigas - rectangulares, circulares, em forma de I e anulares de parede fina - ao mesmo tempo que sugere formas de melhorar o desempenho das vigas através de um melhor design e utilização de materiais. Saiba como interagem as tensões de corte e de flexão e descubra dicas práticas para otimizar a construção e aplicação de vigas.
Existe um momento fletor e uma força de corte na secção transversal de uma viga sujeita a uma força transversal, resultando em tensões normais e tensões de corte na secção transversal. A tensão de corte à flexão de várias secções de vigas comuns será discutida a seguir.
Um pequeno segmento com um comprimento dx é cortado da viga sob flexão por força transversal. A viga não tem carga e as forças de corte em ambos os lados do segmento são iguais mas em direcções opostas. O momento fletor na secção direita é maior do que na secção esquerda, resultando em tensões normais diferentes nas duas secções.
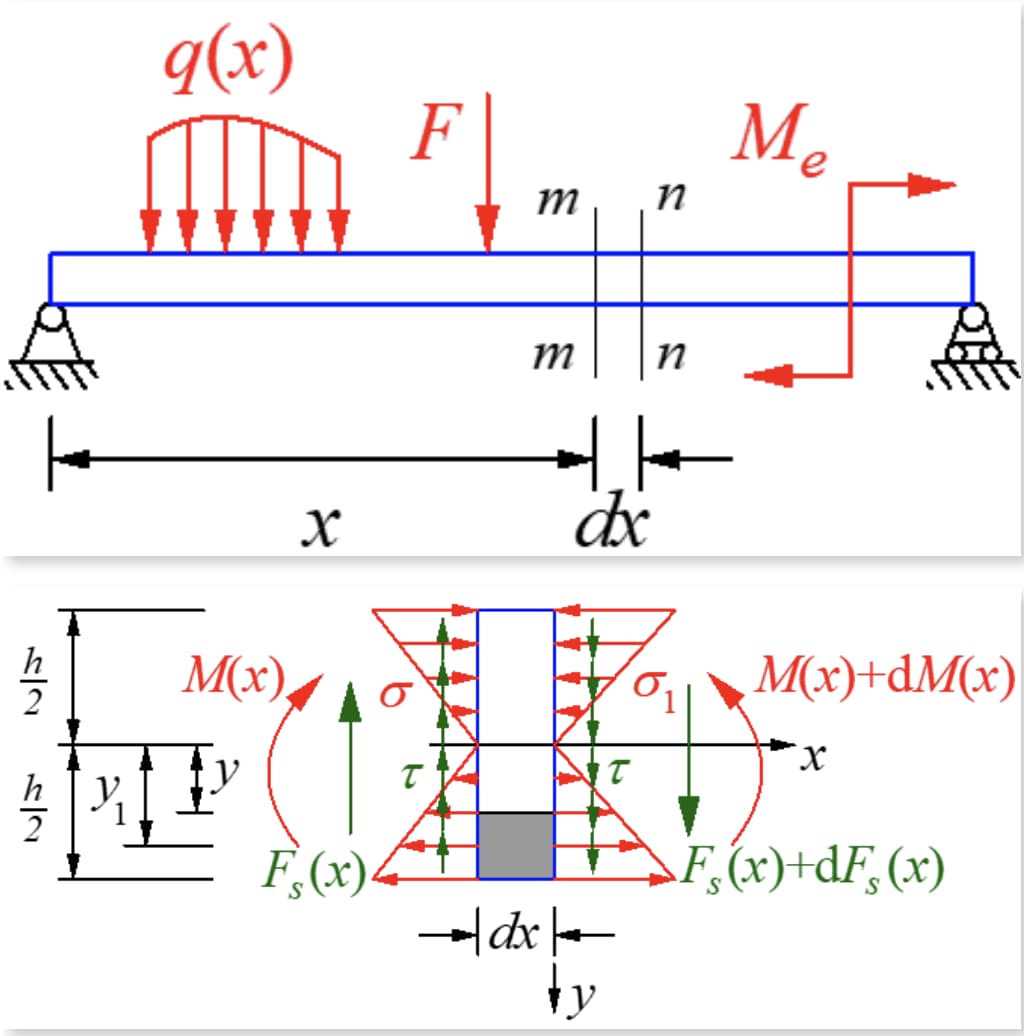
Para uma secção retangular estreita, a tensão de corte é tangente à fronteira em ambos os lados da viga devido à ausência de tensão de corte no lado. Isto significa que, como a viga está simetricamente dobrada e paralela à fronteira, a tensão de corte no eixo y do eixo de simetria deve estar na direção y e muda pouco ao longo da direção da largura.
Por conseguinte, são feitas as seguintes suposições sobre a lei de distribuição da tensão de corte na secção transversal:
Quando a relação altura/largura da secção é superior a 2, a solução baseada na hipótese acima é suficientemente precisa em comparação com a solução exacta da teoria elástica.
De acordo com o teorema da reciprocidade da tensão de corte, deve haver uma tensão de corte igual à dimensão da secção transversal na secção longitudinal perpendicular à secção transversal. Cortar um micro segmento ao longo do plano longitudinal com o eixo neutro do momento afastado de y, e tomar o micro elemento no lado inferior do plano longitudinal. As forças são as indicadas na figura abaixo.
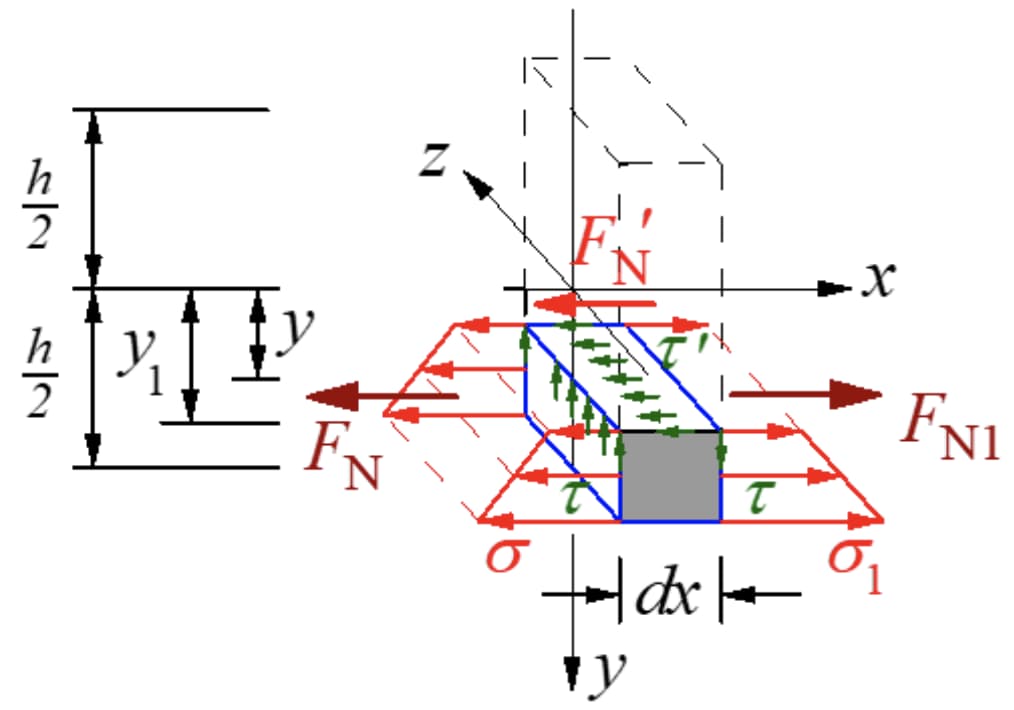
A força resultante da tensão normal na secção esquerda é:
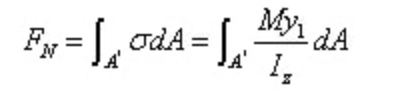
A força resultante da tensão normal na secção direita é：
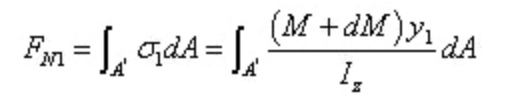
É evidente que as duas resultantes são de dimensões diferentes. Deve existir uma força ao longo da direção axial na secção longitudinal para manter o equilíbrio do micro segmento. Esta força é o resultado da tensão de cisalhamento, confirmando a presença de tensão de cisalhamento na secção longitudinal.
Como dx é uma quantidade pequena, deixe a tensão de cisalhamento no plano longitudinal ser distribuída uniformemente：
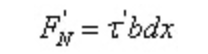
De acordo com as condições de equilíbrio：
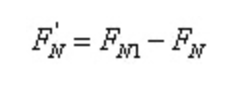
Isto é,
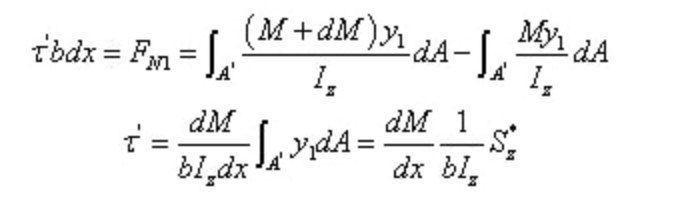
Entre,
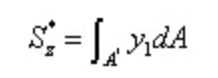
Do teorema recíproco da tensão de corte e da relação diferencial entre a força de corte e o momento fletor:
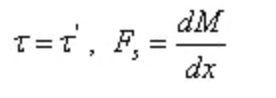
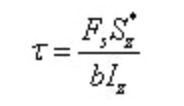
Dos quais:
Entre,
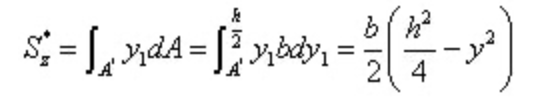
Substituir na fórmula de cálculo da tensão de cisalhamento
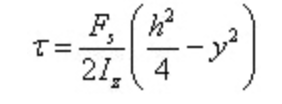
A tensão de corte é distribuída em parábola ao longo da altura da secção.
Quando y=0, existe a tensão de corte máxima na secção no eixo neutro
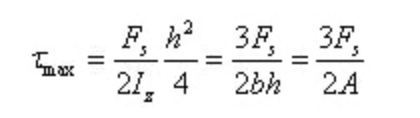
A deformação angular é
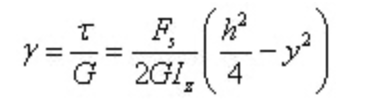
Pode ver-se que a deformação angular é também uma parábola distribuída ao longo da altura da secção.
Neste momento, a forma de deformação da secção transversal quando a força transversal se dobra é mostrada na figura abaixo, o que verifica que a deformação por flexão da força transversal não cumpre o pressuposto do plano.
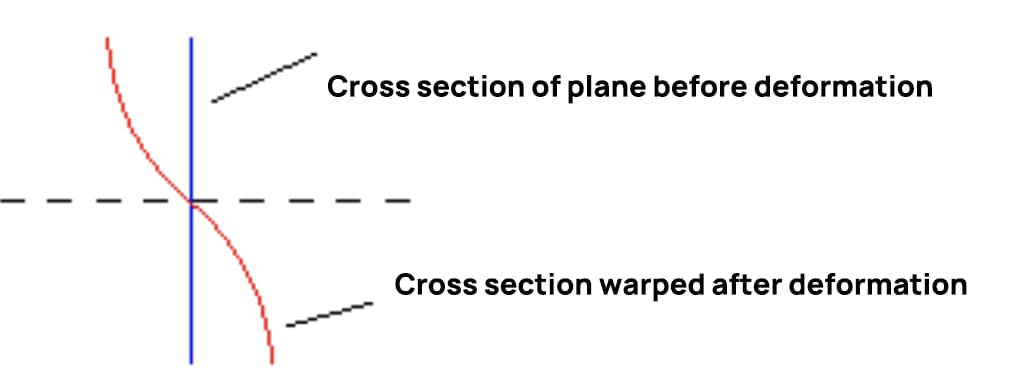
Quando a força de cisalhamento permanece constante, a tensão de cisalhamento em secções transversais consecutivas é igual e o grau de empenamento também é igual. O comprimento das fibras longitudinais não se altera devido ao empenamento da secção, pelo que não resultará em tensão normal adicional. Se a força de cisalhamento mudar com a posição da secção, o grau de empenamento em duas secções consecutivas será diferente, levando a uma tensão normal adicional na secção.
Para secções simétricas de outras formas, a solução aproximada da tensão de corte pode ser derivada utilizando o método acima.
Para uma secção retangular, na fórmula de cálculo da tensão, a largura da secção (b) é constante, e o momento estático de metade da área da secção transversal de um lado do eixo neutro para o eixo neutro é o maior. Como resultado, a tensão de corte em cada ponto do eixo neutro é a maior.
Para secções simétricas de outras formas, a tensão de corte máxima na secção transversal está normalmente localizada em vários pontos do eixo neutro, com exceção das secções com largura significativamente aumentada no eixo neutro (como secções transversais) ou algumas secções com largura variável (como secções de triângulo isósceles).
Por isso, para vigas de secção circular, anular e em forma de I, a tensão de corte máxima em cada ponto do eixo neutro será discutida mais adiante.
A tensão de cisalhamento em cada ponto da borda de uma secção circular é tangente à circunferência, de acordo com o teorema recíproco da tensão de cisalhamento. Em cada ponto do eixo de simetria, a tensão de corte deve estar na direção y. A distribuição da tensão de corte pode ser assumida como convergindo para um ponto no eixo de simetria para cada ponto ao longo da largura y a partir do eixo neutro, e os componentes da tensão de corte ao longo da direção Y em cada ponto ao longo da largura são iguais.
A tensão de corte máxima da secção circular está ainda no eixo neutro e a sua direção é paralela à força externa, com o mesmo valor em cada ponto do eixo neutro.
A tensão de corte máxima é
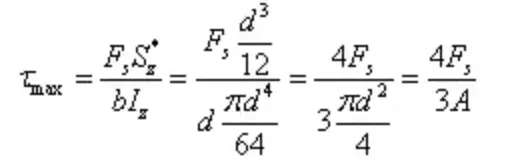
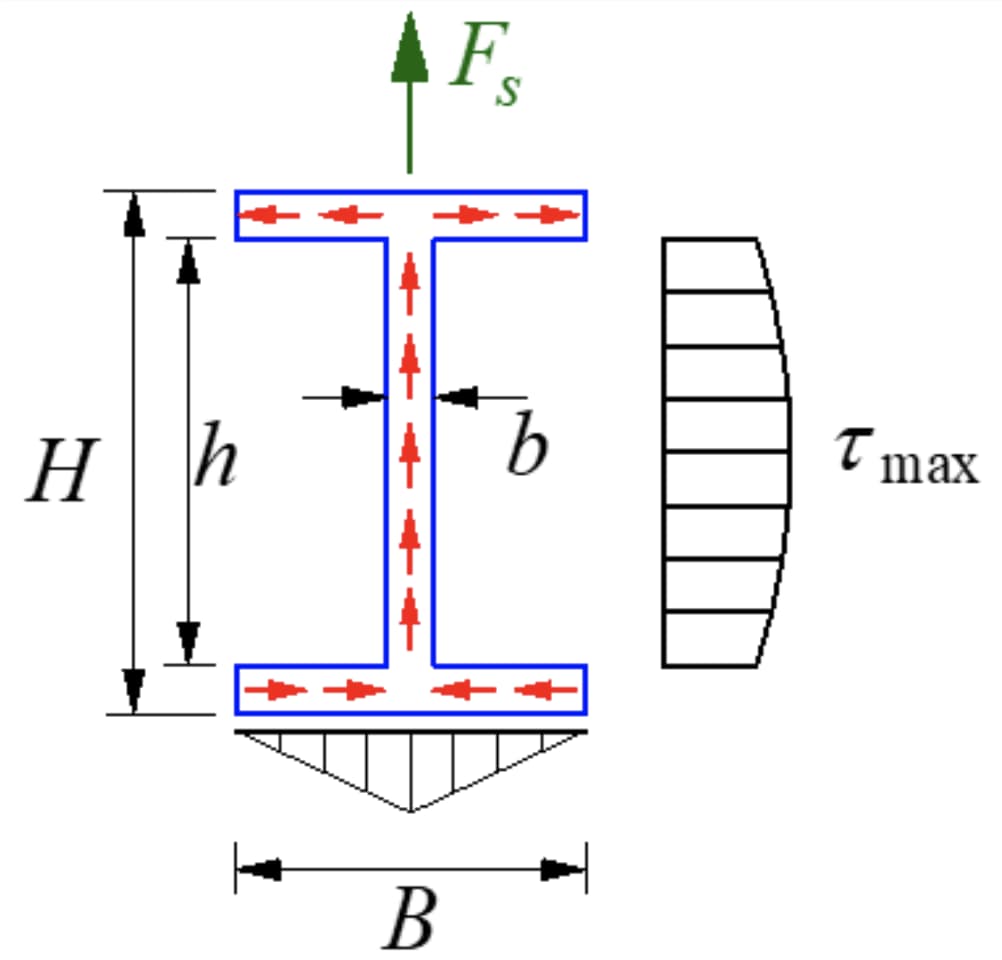
A secção em forma de I é uma secção aberta de paredes finas com uma distribuição de tensões como se mostra na figura. A magnitude da tensão de cisalhamento ao longo da espessura da parede é igual, conhecida como fluxo de tensão de cisalhamento, fluindo na direção do cisalhamento.
A componente da tensão de corte paralela ao eixo y no banzo é secundária e negligenciável, com o foco principal na componente paralela ao lado longo do banzo. A tensão de corte na alma tem uma distribuição parabólica, com o seu tamanho indicado na figura.
A tensão de corte máxima situa-se no eixo neutro.
Em caso de Aço em forma de I, a tensão de corte máxima:
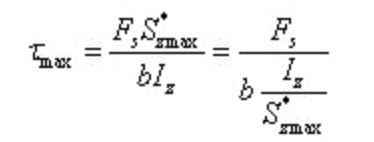
Em que, b é a espessura da teia e Iz/s*zmax pode ser obtido através da tabela de perfis de aço.
Se se tratar de uma secção em forma de I composta por três rectângulos longos e estreitos, as tensões de corte máximas e mínimas na alma podem ser obtidas da seguinte forma
A partir das duas fórmulas anteriores, pode verificar-se que a largura da alma é muito menor do que a largura do flange, pelo que a tensão de corte máxima na alma não é muito diferente da tensão de corte mínima.
Por conseguinte, pode considerar-se que a tensão de corte na alma está distribuída de forma aproximadamente uniforme.
A tensão de corte resultante na alma é responsável por 95-97% da força de corte total, e a força de corte na secção transversal é suportada principalmente pela alma.
Uma vez que a alma suporta quase toda a força de corte na secção e a tensão de corte na alma está distribuída de forma quase uniforme, a tensão de corte máxima pode ser calculada aproximadamente dividindo a força de corte pela área da secção transversal do pólo ventral:
Ao mesmo tempo, toda a área de Viga em I O flange está mais afastado do eixo neutro e a tensão normal em cada ponto é relativamente grande, pelo que o flange suporta a maior parte do momento fletor na secção.
A espessura da secção anular de parede fina é d, o raio médio do anel é r, e a espessura é muito inferior ao raio médio, pelo que se pode assumir que:
A tensão de corte na secção transversal é igual ao longo da espessura da parede;
A direção da tensão de corte é tangente à linha central da secção, e a direção do fluxo da tensão de corte é ao longo da direção de corte.
A tensão de corte máxima está localizada no eixo neutro:
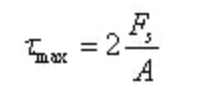
Em que, A é a área da secção anular.
Condição de resistência à tensão normal de flexão:
Para secções neutras axissimétricas, a tensão normal de tração máxima e a tensão normal de compressão máxima são iguais.
Os materiais plásticos são normalmente utilizados e as suas condições de resistência:
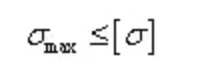
Quanto à secção com eixo neutro assimétrico, a tensão normal de tração máxima e a tensão normal de compressão máxima não são iguais.
Os materiais frágeis são normalmente utilizados e as suas condições de resistência:
A condição de resistência da tensão de cisalhamento de flexão é:
A tensão normal de flexão é o principal fator de controlo da viga.
Por conseguinte, a condição de resistência da tensão normal de flexão é frequentemente a principal base para o dimensionamento de vigas.
A partir da condição de resistência, para melhorar a capacidade de suporte da viga, devem ser considerados dois aspectos:
Por um lado, a tensão da viga deve ser razoavelmente organizada para reduzir o momento fletor máximo;
Por outro lado, é adoptada uma forma de secção razoável para melhorar o coeficiente de secção de flexão da secção e utilizar plenamente as propriedades do material.
Melhorar o estado de tensão da viga e tentar reduzir o momento fletor máximo da viga.
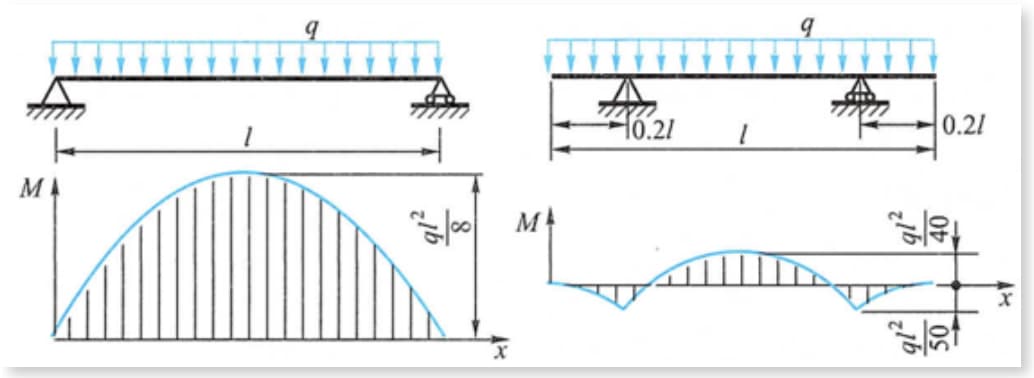
Como mostra a figura, o momento fletor máximo na viga sob carga uniforme é muito reduzido quando o apoio é deslocado para o interior a uma certa distância das posições de ambas as extremidades da viga.
Por exemplo, a viga e o contentor cilíndrico da grua de pórtico, cujo ponto de apoio se desloca ligeiramente para o meio, podem conseguir o efeito de reduzir o momento fletor máximo.
Quanto maior for o coeficiente de flexão da secção, menor será a tensão e maior será a capacidade de carga da viga.
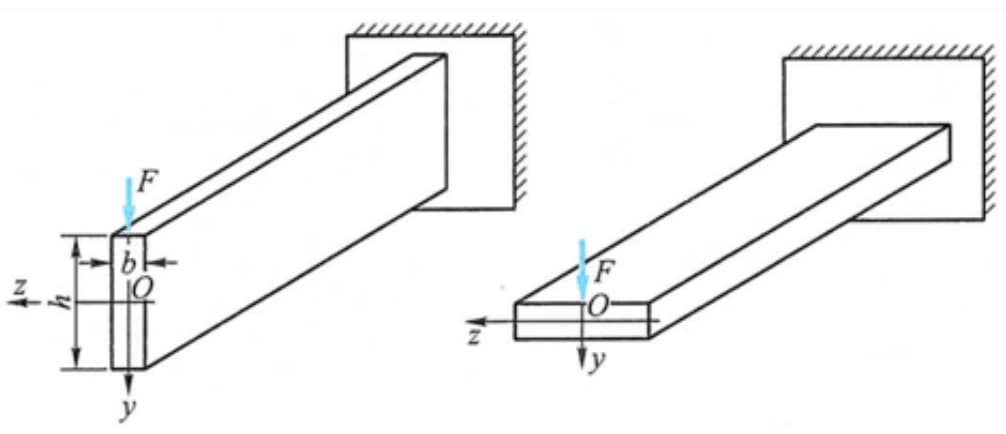
Por exemplo, quando a viga é carregada na direção vertical, o coeficiente de flexão da secção é maior quando a secção é colocada na vertical, pelo que é mais razoável colocá-la na vertical do que na horizontal.
Ao mesmo tempo que melhoramos o coeficiente de secção de flexão da secção, esperamos também utilizar menos materiais para conseguir uma maior economia.
Por conseguinte, a relação entre o coeficiente de flexão da secção e a área da secção é geralmente utilizada para medir a racionalidade da conceção da secção.
Para a mesma área de secção transversal, a secção retangular (altura superior à largura) é mais razoável do que a secção circular, enquanto a secção em forma de I ou a secção em caixa é mais razoável do que a secção retangular.
Por conseguinte, para tirar o máximo partido dos materiais, estes devem ser colocados o mais longe possível do eixo neutro.
Ao discutir a forma razoável da secção, o propriedades mecânicas do material também deve ser tida em conta.
Os materiais com a mesma resistência à tração e à compressão (como o aço de baixo teor de carbono) devem adotar secções neutras axissimétricas, tais como circulares, rectangulares, em forma de I, em caixa, etc.
Desta forma, a tensão máxima de tração e a tensão máxima de compressão nos bordos superior e inferior da secção podem ser iguais.
Para materiais com resistências desiguais à tração e à compressão (como o ferro fundido, o cimento, etc.), deve ser adoptada a forma de secção com o eixo neutro inclinado para o lado da tração.
As vigas acima referidas têm todas a mesma secção e o coeficiente de flexão da secção é constante, mas, em geral, o momento fletor de cada secção da viga varia com a posição da secção.
O dimensionamento da secção de uma viga reta igual deve ser efectuado de acordo com o momento fletor máximo, e a sua tensão máxima está próxima da tensão admissível.
O momento fletor nas outras secções é pequeno, pelo que a tensão é pequena e o material não é totalmente utilizado.
Para poupar materiais e reduzir o peso próprio, a dimensão da secção pode ser alterada de modo a que o coeficiente da secção de flexão se altere com o momento de flexão.
Uma secção maior é utilizada onde o momento fletor é maior, enquanto uma secção menor é utilizada onde o momento fletor é menor.
Este tipo de viga cuja secção muda ao longo do eixo é designado por viga de secção variável.
Se a tensão normal máxima em cada secção transversal de uma viga de secção variável for igual e igual à tensão admissível, designa-se por viga de igual resistência.
Como fundador da MachineMFG, dediquei mais de uma década da minha carreira à indústria metalúrgica. A minha vasta experiência permitiu-me tornar-me um especialista nos domínios do fabrico de chapas metálicas, maquinagem, engenharia mecânica e máquinas-ferramentas para metais. Estou constantemente a pensar, a ler e a escrever sobre estes assuntos, esforçando-me constantemente por me manter na vanguarda da minha área. Deixe que os meus conhecimentos e experiência sejam uma mais-valia para a sua empresa.
PT 
EN 
AR 
DE 
ES 
FR 
IT 
JA 
NL 
PT_BR 
RU 
KO