Como é que uma viga de aço suporta o peso de uma ponte ou a pressão de uma grua? Este artigo analisa os cálculos da resistência à flexão de secções de aço, explicando os conceitos de fases elásticas, elástico-plásticas e plásticas. Ao compreender a resistência e a rigidez das diferentes secções, os leitores ficarão a saber como garantir a segurança e a estabilidade das estruturas sob várias cargas. Mergulhe para compreender os princípios fundamentais que mantêm as nossas construções de pé e resistentes.
1. Conceito:
Suporta cargas laterais, tais como vigas de pavimentos, vigas de gruas, madres, pontes, etc.
2. Classificação:
(1) Teia sólida：
Secção de aço em forma de H: Fácil de processar, simples de fabricar e de baixo custo.
Secção composta: Quando o aço em forma de H não pode cumprir os requisitos de resistência e rigidez.
(2) Estrutura da rede:
Quando o vão é superior a 40 m, é preferível utilizar uma treliça treliçada.
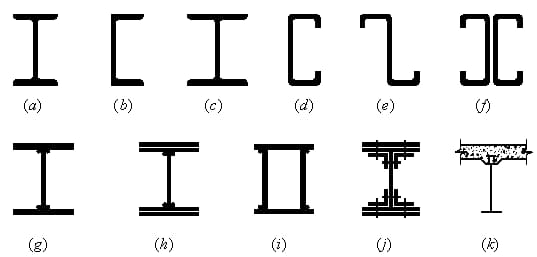
3. Grelha de vigas:
Um sistema plano composto por vigas principais e secundárias que se intersectam vertical e horizontalmente.
(1) Grelha de feixe simplificada: Feixe principal único.
(2) Grelha de vigas ordinárias: Dividida em vigas principais e secundárias.
(3) Grelha de vigas compostas: Dividida em vigas principais, vigas secundárias horizontais e verticais.
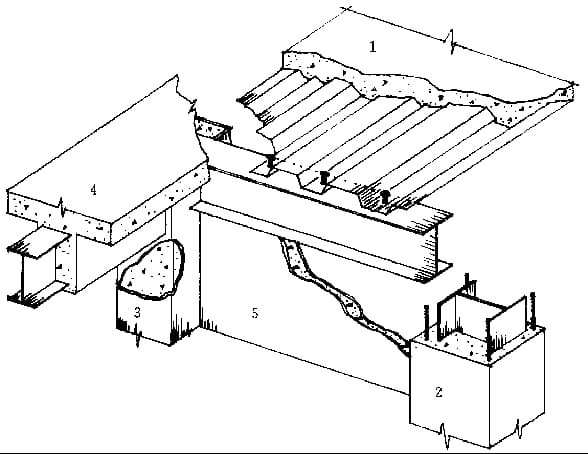
4. Interação entre vigas e placas:
(1) Co-working: Laje de pavimento composta.
(2) Trabalhos não cooperativos: Laje geral de betão armado.
O desenvolvimento da tensão normal na secção transversal pode ser dividido em três fases:
(1) Estágio elástico: Sob carga dinâmica.
(2) Estágio elástico-plástico: Sob carga estática ou carga dinâmica indireta.
(3) Fase plástica:
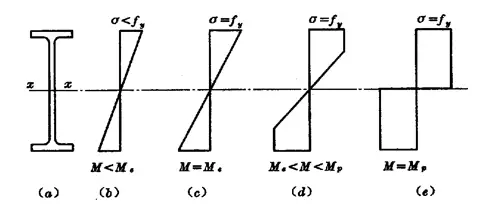
Capacidade de flexão durante a fase elástico-plástica de uma secção transversal:
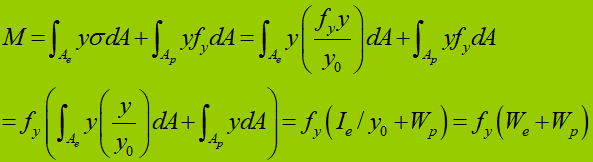
Para uma secção retangular:
(1) Fase elástica:
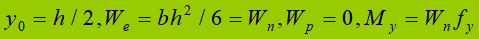
(2) Fase de plástico:
(3) Estágio elástico-plástico:
Fator de forma da secção:
Desenvolvimento plástico de secção parcial (1/4 de secção, a = h/8) como estado limite:
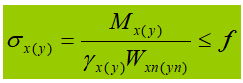
Na fórmula:
γ é o fator de segurança parcial para o momento, que pode ser determinado com base no Quadro 5.1 da Secção 5 do código de dimensionamento.
Há dois casos em que o fator de segurança parcial para o momento deve ser considerado como 1,0.
Método:
S:
A resistência ao cisalhamento pode ser calculada utilizando a teoria do fluxo de cisalhamento, assumindo que é uniformemente distribuída ao longo da direção da espessura da parede fina.
(1) Ao calcular a tensão de corte vertical em qualquer ponto da alma, é necessário calcular o momento de inércia da área da secção bruta acima ou abaixo desse ponto em relação ao eixo neutro x.
(2) Ao calcular a tensão de corte horizontal em qualquer ponto do verdugo, é necessário calcular o momento de inércia da área da secção bruta à esquerda ou à direita desse ponto em relação ao eixo neutro x.
Onde tw é a espessura da secção no local onde a tensão de corte está a ser calculada.
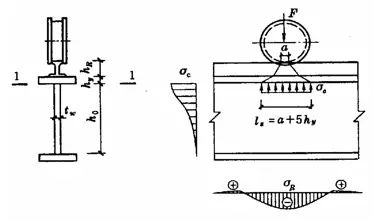
Quando o banzo de uma viga está sujeito a uma grande carga central fixa (incluindo as reacções de apoio) e não existem reforços, de acordo com a Figura 5-5 (a), ou quando está sujeito a uma carga concentrada móvel (como a pressão da roda da grua), de acordo com a Figura 5-5 (b), deve calcular-se a resistência à compressão local no bordo da altura da alma. Partindo do princípio de que a carga concentrada se estende desde o ponto de aplicação até um intervalo de altura hy numa proporção de 1:2,5, e espalha-se numa proporção de 1:1 numa gama de alturas de hRé uniformemente distribuído pela altura da teia cálculo do bordo. O σc é muito próximo da pressão local máxima teórica. A resistência local à compressão pode ser calculada pela seguinte fórmula:
Na fórmula,
Quando o cálculo não é satisfatório, a carga concentrada fixa ou o apoio podem ser reforçados através da colocação de reforços transversais ou da modificação da dimensão da secção. No entanto, quando suportam cargas concentradas móveis, apenas a dimensão da secção pode ser modificada.
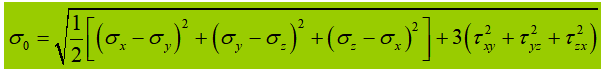
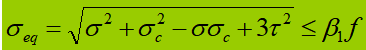
Quando o vibrador do abdómen é sujeito a uma tensão normal significativa, a uma tensão de corte ou a uma tensão de compressão local na altura calculada, é necessário calcular a tensão equivalente nesse local.
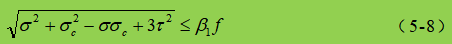
Na fórmula:
σ, τ, σc - tensão normal de flexão, tensão de corte e tensão de compressão local no mesmo ponto da altura de cálculo da placa do abdómen, positiva para a tensão de tração e negativa para a tensão de compressão;
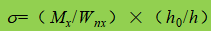
β1 - coeficiente para aumentar o valor de projeto da resistência à compressão num ponto local. Quando σ e σc têm o mesmo sinal ou σc=0, β1=1,1; quando σ e σc têm sinais opostos, β1=1.2.
Fenómeno de instabilidade global:
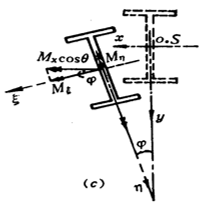
Análise do mecanismo:
Depois de a viga ser deformada por flexão, o banzo superior é sujeito a compressão. Devido à rigidez lateral insuficiente da viga, esta sofre uma deformação por encurvadura lateral. A deformação por flexão no plano causada pelo momento também ocorre juntamente com a deformação por torção devido à flexão desigual de cima para baixo da secção da viga.
Por conseguinte, a instabilidade global da viga assume a forma de encurvadura por flexão-torção ou, mais exatamente, de encurvadura por flexão lateral e por torção.
(1) C1, C2, C3 - Relacionado com o tipo de carga
(2) Iy, Iw, It - Momento de inércia da secção transversal
(3) L - Comprimento não apoiado na direção lateral
(4) a - Localização do ponto de ação na direção da altura.
(5) 
| Condição de carga | Coeficiente | ||
| G | C2 | G | |
| Carga concentrada a meio do vão | 1.35 | 0.55 | 0.41 |
| Carga uniformemente distribuída ao longo de todo o vão | 1.13 | 0.46 | 0.53 |
| Flexão pura | 1.00 | 0.00 | 1.00 |
Os principais factores que afectam a estabilidade global das vigas de aço são:
(1) O comprimento não apoiado na direção lateral ou a distância L1 entre o ponto de apoio lateral do banzo comprimido. Quanto mais pequeno for o valor de L1, melhor será a estabilidade global da viga e mais elevado será o momento fletor crítico.
(2) A dimensão da secção transversal, incluindo os diferentes momentos de inércia. Quanto maior for o momento de inércia, melhor será a estabilidade global da viga. Em particular, o aumento da largura do banzo comprimido b1 pode também aumentar o valor de βy na fórmula.
(3) Os constrangimentos da secção pelos apoios extremos da viga. Se os constrangimentos à rotação em torno do eixo y da secção puderem ser melhorados, a estabilidade global da viga será consideravelmente melhorada.
(4) Tipo de carga: Flexão pura, carga uniformemente distribuída, carga concentrada a meio do vão.
(5) A localização do ponto de ação da carga ao longo da direção da altura da secção transversal, um valor; negativo para o banzo superior e positivo para o banzo inferior.
Flexão num único plano:
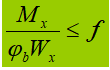
1. Secção transversal soldada em forma de I, biaxialmente simétrica, pura carga de flexão.
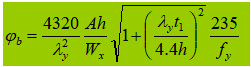
2. Secção transversal soldada em forma de I, uniaxialmente simétrica (efeitos da secção transversal assimétrica e de diferentes cargas)
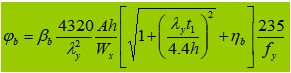
Se φb>0,6, o coeficiente de estabilidade é considerado como:
3. Viga laminada de aço ordinário em forma de I com apoio simples.
4. Viga de aço de canal laminado a quente com apoio simples.
5. Uma viga em consola simétrica de dois eixos em forma de I.
O banzo comprimido da viga é coberto por um tabuleiro (betão armado ou chapa de aço) e firmemente ligados para impedir a deslocação lateral da flange comprimida.
Para vigas H ou I simplesmente apoiadas, a relação entre o comprimento livre L1 e a largura b do banzo comprimido não excede o valor especificado no Quadro 5.4.
Quadro 5.4: Valor máximo de L1/b1 para o qual o cálculo da estabilidade global não é necessário para vigas H ou I simplesmente apoiadas.
| Grau de aço | Uma viga sem pontos de apoio laterais no meio do vão. | Uma viga com um banzo sujeito a compressão ao longo do vão e com pontos de apoio laterais, independentemente do local onde a carga é aplicada. | |
| A carga é aplicada à flange. | A carga é aplicada na flange inferior. | ||
| Q235 | 13.0 | 20.0 | 16.0 |
| Q345 | 10.5 | 16.5 | 13.0 |
| Q39 | 10.0 | 15.5 | 12.5 |
| Q420 | 9.5 | 15.0 | 12.0 |
1. Determinar se é necessária a verificação da estabilidade global.
2. Calcular os parâmetros da secção.
3) Obter o coeficiente do momento fletor crítico equivalente βb de acordo com as condições de carga.
4. Substituir os valores nas fórmulas para obter o coeficiente de estabilidade global ϕb e verificar a estabilidade global.
Exemplo: 5-2，5-3
Placa de flange: A carga é relativamente simples e a estabilidade local é assegurada pela limitação da relação largura/espessura da placa.
Placa Web: A carga é complexa e, para cumprir os requisitos de resistência, a altura da secção é frequentemente grande. Se continuarmos a limitar a relação entre a altura e a espessura da chapa de alma, o valor da chapa de alma será muito grande, o que não é económico. Por conseguinte, os reforços são geralmente utilizados para reduzir o tamanho da placa e melhorar a capacidade de suporte da estabilidade local.
1. Reforços transversais
2. Reforços longitudinais
3. Reforços curtos
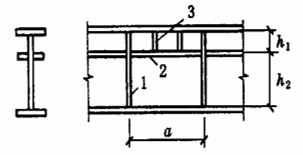
Princípio de conceção: Princípio da igualdade de forças.
De acordo com o dimensionamento elástico (com γ=1,0 para não considerar o desenvolvimento plástico), devido à influência de tensão residuala secção transversal real entrou na fase elástico-plástica. A "Especificação" toma Et=0.7E.
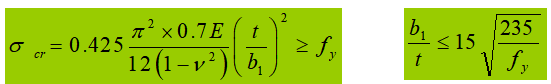
Se for considerado o desenvolvimento plástico (γ > 1,0), o desenvolvimento plástico será maior, e Et=0.5E.
| Não. | O estado da placa de rede. | Especificações da disposição dos reforços | |
| 1 | 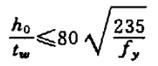 | στ=0 | Os reforços podem ser omitidos. |
| 2 | στ≠0 | Recomenda-se a instalação de reforços transversais que cumpram os requisitos estruturais e de cálculo. | |
| 3 |  | Recomenda-se a instalação de reforços transversais que cumpram os requisitos estruturais e de cálculo. | |
| 4 |  A flange comprimida está protegida contra a torção. | Os reforços longitudinais devem ser adicionados na zona de compressão da secção onde a tensão de flexão é elevada, cumprindo os requisitos estruturais e de cálculo. | |
| 5 | 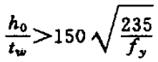 A flange comprimida pode torcer-se livremente. | ||
| 6 | Quando necessário para efeitos de cálculo. | ||
| 7 | Quando a tensão de compressão local é elevada. | Se necessário, devem ser colocados reforços curtos na zona de compressão para cumprir os requisitos estruturais e de cálculo. | |
| 8 | No apoio da viga | É aconselhável instalar reforços de suporte que cumpram os requisitos estruturais e de cálculo. | |
| 9 | Quando o banzo está sujeito a uma grande carga concentrada fixa. | ||
| 10 | Em todo o caso |  | |
1. Encurvadura de placas compostas sob tensão
Apenas a chapa de alma com reforços transversais está configurada.
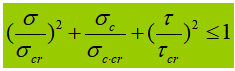
A chapa de alma é configurada com reforços transversais e longitudinais ao mesmo tempo.
(1) Entre o banzo comprimido e os reforços longitudinais.
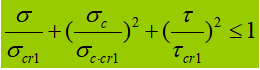
(2) Entre o banzo de tração e os reforços longitudinais.
Os reforços transversais curtos são instalados entre a flange comprimida e os reforços longitudinais.
2. Requisitos de construção dos reforços para a chapa de alma
(1) Reforços transversais em aço dispostos aos pares em ambos os lados da chapa da alma.
Largura saliente para o exterior:
Espessura:
(2) Reforços transversais de aço configurados num dos lados da chapa da alma.
Largura saliente para o exterior: deve ser superior a 1,2 vezes o valor calculado de acordo com a fórmula acima.
Espessura: não deve ser inferior a 1/15 da sua largura saliente para o exterior.
(3) Na chapa de alma reforçada com reforços transversais e longitudinais, os reforços longitudinais devem ser desligados nas suas intersecções enquanto os reforços transversais permanecem contínuos.
O momento de inércia em torno do eixo z também deve satisfazer:
(4) Tratamento da extremidade dos reforços transversais:
3. Reforços de suporte
(1) Cálculo da estabilidade:
A estabilidade dos reforços para apoio é calculada como um elemento de compressão sujeito a cargas concentradas fixas ou a reacções de apoio da viga ao longo do seu eixo. A área da secção transversal A deste elemento de compressão inclui tanto o reforço como a área da chapa de alma dentro de 15tw em cada lado do reforço. O comprimento de cálculo é considerado aproximadamente como h0.
(2) Cálculo da resistência à compressão:
A extremidade dos reforços de apoio da viga deve ser calculada em função da carga concentrada fixa ou da reação de apoio que suportam. Quando a extremidade dos reforços é aparada de forma plana e apertada, a tensão de compressão na face da extremidade deve ser calculada da seguinte forma
onde:
Etapas de projeto para reforços transversais de chapa de alma:
1. Determinar se é necessário instalar barras transversais;
2. Instalar as travessas e determinar o espaçamento a, bs, ts;
3. Verificar o estado de tensão composto da chapa de alma;
4. Verificar o reforço de apoio: incluindo a soldadura (ligação entre as travessas e a placa de alma), a verificação da estabilidade à compressão axial (estabilização fora do plano do eixo z) e a verificação da resistência.
Exemplo 5-3: Com base nas condições e nos resultados do Exemplo 5-2, verificar se a secção da viga principal apresentada na Figura 5-9(b) cumpre os requisitos. A viga principal é uma viga simplesmente apoiada em ambas as extremidades, feita de aço Q235 e soldada com eléctrodos de soldadura manual da série E43.
Solução:
1. Capacidade de carga da viga principal:
O diagrama de cálculo simplificado da viga principal é apresentado na figura 5-9(a). A pressão exercida na viga principal pelas vigas secundárias de ambos os lados é de 2×73,69+2×2,33=152,04 kN, e a pressão das vigas secundárias na extremidade da viga é metade da pressão da viga secundária do meio.
A reação de apoio da viga principal é R=2×152,04=304,08 kN.
O momento fletor máximo da viga é M=(304,08-76,02)x5-152,04×2,5=760,2 kN.m
2. Calcular as características da secção:
A=131,2 cm², Ix=145449 cm⁴, Wx=3513,3 cm³. O peso próprio da viga principal é 131,2×10²x7850x10-⁶x1,2=123,6 kg/m=1,211 kN/m. O fator de 1,2 é para considerar o aumento do coeficiente do reforço da viga principal. O valor de projeto do momento fletor após considerar o peso da viga principal é M=760.2+1.2×1.211×10²/8=760.2+18.2=778.4 kN-m.
Considerando que o valor de projeto da força de reação no apoio, depois de contabilizado o peso próprio da viga principal, é R=304,08+1,2×1,211×10/2=304,08+7,27=311,3kN.
3. Controlo da força
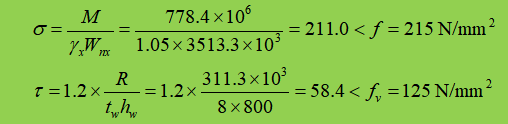
Os reforços de apoio são fornecidos na ligação da viga secundária e não existe tensão de compressão local. Além disso, uma vez que a tensão de corte é relativamente pequena, não é necessário verificar outras tensões convertidas na secção.
4. Existe uma placa rígida na viga secundária, que assegura a estabilidade da viga secundária e pode servir de ponto de apoio lateral para a viga principal.
Nesta altura, uma vez que l1/b1=2500/240=10,4<16, a estabilidade global pode ser assegurada sem cálculos.
5. Controlo da rigidez
O valor normalizado total da carga transmitida pela viga secundária é FT=(15.5+0.52)×7.5=120.2kN, therefore,
O valor normalizado total da carga transmitida pela viga secundária é FQ=2.5×4.2×7.5=78.75kN, therefore,
6. Estabilidade local
Flange: b/t=(120-4)/14=8,3<13, que cumpre o requisito de estabilidade local, e γx pode ser considerado como 1,05; Placa de rede: h0/tw=800/8=100, é necessário prever reforços transversais, os pormenores são omitidos.
Após a deformação da placa fina, são geradas tensões transversais de tração no centro da placa, o que restringe ainda mais a deformação longitudinal por flexão da placa, permitindo-lhe continuar a suportar o aumento da pressão.
1. Capacidade de suporte ao corte após a encurvadura: Fórmula (5-94)
2. A capacidade de suporte ao cisalhamento inclui duas partes: Força de corte de encurvadura (resistência à encurvadura) + força de corte do campo de tensão (resistência após a encurvadura).
3. Força de cisalhamento do campo de tensão:
(1) Método do campo de tensão (complexo);
(2) Especificação do código.
Considerando que a capacidade de suporte de flexão da chapa de alma diminui ligeiramente após a encurvadura.
Dois pressupostos:
(1) Altura efectiva;
(2) Simetria entre a zona de tração e a zona de compressão.
A fórmula para calcular a capacidade de suporte:
Na fórmula,
Isto indica que:
(1) Quando M na secção é inferior a Mf que o banzo pode suportar, a chapa de alma pode suportar a força de corte Vu;
(2) Quando V na secção for inferior a 0,5Vu, tomar M = Meu.
(1) Se os reforços de apoio por si só não puderem satisfazer a Equação (5.99), devem ser adicionados reforços transversais emparelhados em ambos os lados da alma para reduzir o comprimento da região de encurvadura.
(2) As dimensões da secção transversal dos reforços transversais devem cumprir os requisitos de construção para os reforços de alma, de acordo com a equação 5.85.
(3) De acordo com as especificações da estrutura de aço, o reforço transversal central deve ser tratado como um elemento de compressão axial e a sua estabilidade fora do plano da alma deve ser calculada com base na força axial utilizando a seguinte fórmula:
Quando o reforço é sujeito a uma carga transversal concentrada F, Ns deve ser aumentado em F.
Calcular o valor de projeto do momento fletor máximo Mmáximo para a viga com base nas condições reais.
Determinar o módulo de secção necessário com base na resistência à flexão e na estabilidade global:
Determinar a secção de aço com base nas tabelas de secções.
Verificação da secção:
(1) Verificação da resistência: flexão, cisalhamento, compressão local e tensão equivalente.
(2) Verificação da rigidez: verificar a relação entre a deformação e o vão da viga.
(3) Verificação da estabilidade global (a estabilidade local da secção de aço geralmente não requer verificação).
(4) Ajustar a secção com base nos resultados da verificação e efetuar novamente a verificação até que esta cumpra os requisitos de conceção.
1) Determinar o módulo de secção necessário com base nas condições de carga.
2) Determinar a altura do feixe:
Altura selecionada: hmin ≤ h ≤ hmáximo.
3). Determinar a espessura da alma (assumindo que todas as forças de corte são suportadas pela alma), então:
Em alternativa, a espessura da banda pode ser determinada através de fórmulas empíricas:
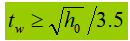
4). Determinar a largura do flange:
Após determinar a espessura da alma, a área do banzo Af pode ser determinado com base nos requisitos de resistência à flexão. Tomando como exemplo uma secção em forma de I:
Uma vez Af é determinado, pode selecionar-se b ou t para determinar o outro valor.
5). Verificação da secção:
6). Cálculo das soldaduras entre a alma e o flange
A soldadura de ligação é utilizada principalmente para resistir flexão-cisalhamentoe o cisalhamento por unidade de comprimento é:
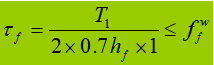
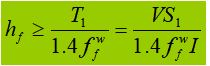
Quando a viga está sujeita a uma carga concentrada fixa sem reforços de apoio, a soldadura do banzo superior suporta a força de corte T1 e a força concentrada F. A força por unidade de comprimento gerada por F é V1:
Objetivo: Para poupar aço e lidar com as alterações do momento fletor.
Métodos de mudança de secção:
Pontos a registar:
1. Classificação:
2. Métodos de união de perfis de aço laminados:
3. Técnicas de união de vigas compósitas:
Principais considerações:
1. Ligações primárias e secundárias de vigas metálicas:
2. Tipos de suporte de vigas:
Principais considerações de conceção:
Como fundador da MachineMFG, dediquei mais de uma década da minha carreira à indústria metalúrgica. A minha vasta experiência permitiu-me tornar-me um especialista nos domínios do fabrico de chapas metálicas, maquinagem, engenharia mecânica e máquinas-ferramentas para metais. Estou constantemente a pensar, a ler e a escrever sobre estes assuntos, esforçando-me constantemente por me manter na vanguarda da minha área. Deixe que os meus conhecimentos e experiência sejam uma mais-valia para a sua empresa.
PT 
EN 
AR 
DE 
ES 
FR 
IT 
NL 
RU