Como calcular o retorno elástico de flexão?

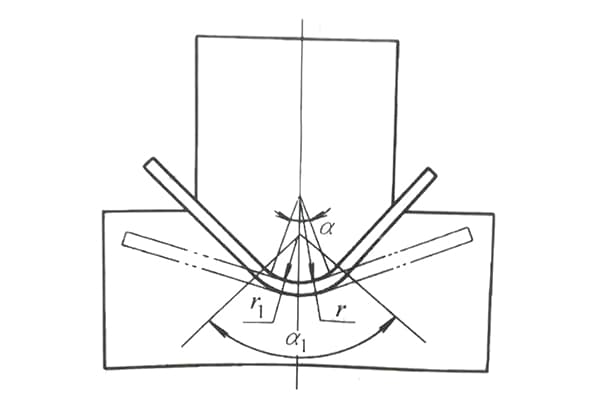
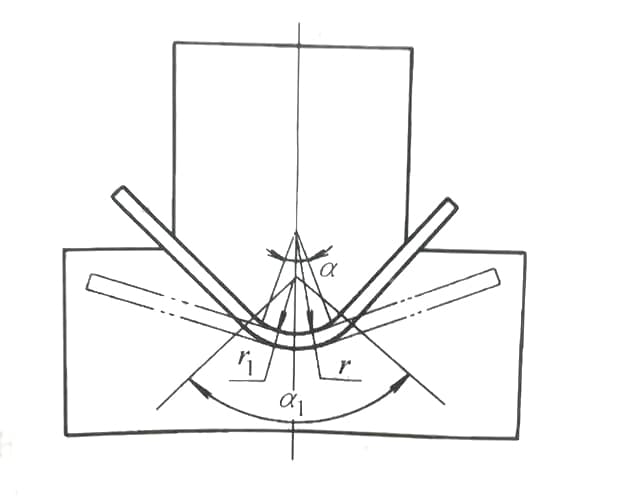
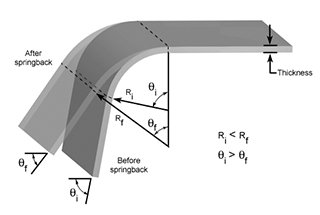
Ao conceber uma matriz de quinagem com um arco interno, a precisão e o comportamento do material são factores críticos frequentemente ignorados nas abordagens convencionais. Muitos projectistas negligenciam completamente o retorno elástico, utilizando o mesmo raio (R) que o produto acabado, ou aplicam um fator de redução rudimentar ao valor R, sem considerar as complexidades das propriedades e geometrias dos materiais.

Por exemplo, uma prática comum para um produto com um valor R original de 1 mm envolve a redução do raio do molde convexo por um fator de 0,8 para materiais mais duros ou 0,9 para materiais mais macios. Esta abordagem simplista, embora por vezes seja eficaz para aplicações básicas, não tem as nuances necessárias para especificações mais exigentes.

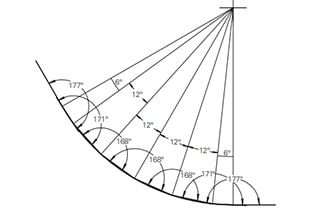
As limitações deste método tornam-se particularmente evidentes quando se trata de materiais finos e grandes raios. Considere-se um produto com uma espessura de 0,5 mm e um raio interno de 200 mm. Nestes casos, a previsão exacta do retorno elástico torna-se um desafio devido à complexa interação entre as propriedades do material, o rácio espessura/raio e o ângulo de flexão.

Para resolver estas limitações e melhorar a precisão no projeto de matrizes, é necessária uma abordagem mais sofisticada. A secção seguinte apresenta uma fórmula universal de retorno elástico que tem em conta vários parâmetros materiais e geométricos, permitindo cálculos mais precisos baseados em dados numéricos. Este método fornece uma base robusta para o projeto de matrizes numa vasta gama de aplicações e materiais.

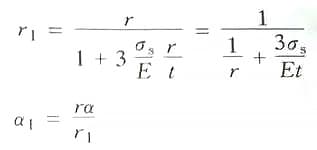
Na fórmula:

• r - raio de filete da peça de trabalho (mm):
• r1 - raio do punção (mm);
• a - o ângulo central do comprimento do arco do filete da peça de trabalho;
• a1 - o ângulo central do comprimento do arco do filete do punção;
• t - espessura do material;
• E - módulo de elasticidade do material;
• σ_s - ponto de escoamento do material.

Assumindo 3σ_s/E=A como coeficiente de simplificação, com valores listados na Tabela 2-27. A fórmula de cálculo para o raio do canto da matriz convexa durante a flexão de barras de secção circular é a seguinte

O valor de A é apresentado no quadro seguinte.

Se os materiais necessários não estiverem disponíveis acima, pode também consultar a tabela abaixo para encontrar os módulo de elasticidade e o limite de elasticidade do material e, em seguida, substituí-los na fórmula acima para cálculo.

É melhor estabelecer uma base de dados de materiais comummente utilizada e obter os parâmetros físicos em falta junto dos fornecedores. Se os parâmetros de módulo de elasticidade e limite de elasticidade estão correctas, a dobragem e o ressalto dos terminais de molas gerais, das peças de aparência e dos perfis são mais precisos.