Já alguma vez se interrogou sobre a forma como os diferentes materiais afectam a dobragem de chapas metálicas? Neste artigo perspicaz, um engenheiro mecânico experiente partilha os seus conhecimentos sobre o impacto dos tipos de materiais, espessura e outros factores nos cálculos de dobragem. Descubra informações valiosas que podem ajudá-lo a otimizar os seus processos de fabrico de chapas metálicas e a obter resultados precisos. Continue a ler para aprender com um especialista do sector e elevar os seus conhecimentos sobre dobragem ao próximo nível!
A nossa calculadora online para dobragem de chapa é uma ferramenta essencial para a metalurgia de precisão, permitindo-lhe determinar rapidamente e com precisão os parâmetros críticos para operações de dobragem de chapa. Esta calculadora avançada fornece informações importantes sobre:
Instruções para uma utilização óptima:
Tire partido desta poderosa calculadora para melhorar o seu processo de fabrico de chapas metálicas, melhorar a precisão, reduzir o desperdício de material e otimizar o seu fluxo de trabalho de produção.
Leitura relacionada:
A dobragem de chapa metálica é um processo fundamental no fabrico de metal que envolve a deformação de uma chapa metálica ao longo de um eixo reto. Este processo é essencial para criar uma vasta gama de produtos metálicos com diferentes formas e funcionalidades. Para conseguir dobras precisas e exactas, é necessário compreender e considerar vários conceitos-chave durante as fases de conceção e fabrico.
O processo de dobragem começa com um desenho detalhado da peça final. Isto implica a criação de modelos 3D utilizando software CAD como o AutoCAD ou o SolidWorks. O desenho deve ter em conta vários factores, incluindo a tolerância de dobragem, os relevos e as linhas de dobragem. Os ficheiros corretamente preparados garantem que o produto final cumpre as especificações e as normas de qualidade pretendidas.
A margem de curvatura representa o comprimento do eixo neutro desde o início até ao fim da curvatura. O fator K é um coeficiente que ajuda a determinar a posição do eixo neutro relativamente à espessura do material. Varia consoante as propriedades do material e o método de dobragem utilizado. Por exemplo, num estudo de caso envolvendo chapa de alumínio, foi utilizado um fator K de 0,3 para obter dobras precisas. Compreender e calcular com precisão a tolerância de dobragem e o fator K é essencial para obter dobras precisas e manter as dimensões gerais da peça.
O raio de curvatura é a curvatura da dobra e é vital para manter a integridade estrutural da chapa metálica. O raio de curvatura mínimo deve, normalmente, ser pelo menos igual à espessura da chapa metálica para evitar deformações ou fissuras. Assegurar raios de curvatura consistentes em todas as curvas também pode contribuir para projectos rentáveis e eficientes.
O retorno elástico é a tendência de uma peça de chapa metálica dobrada para regressar parcialmente à sua forma original após a remoção da força de dobragem. Este fenómeno pode levar a imprecisões nas dimensões finais da peça. Para compensar o retorno elástico, pode ser aplicada uma força adicional através de métodos como o bottoming e o coining. O bottoming comprime a chapa metálica para o fundo da matriz, eliminando efetivamente o retorno elástico. A cunhagem envolve a aplicação de alta pressão para criar uma deformação permanente, reduzindo ainda mais os efeitos do retorno elástico.
O eixo neutro é uma linha imaginária dentro da chapa metálica que não sofre estiramento ou compressão durante a dobragem. A zona de tensão está localizada no exterior da dobragem, onde o material se estica, enquanto a zona de compressão está localizada no interior, onde o material se comprime. A compreensão destas zonas é crucial para cálculos exactos de dobragem e para prever o comportamento do material durante o processo de dobragem.
A orientação da dobra refere-se à direção em que as dobras são feitas. Para uma produção rentável e eficiente, as dobras provenientes do mesmo plano devem ser orientadas na mesma direção. Esta abordagem reduz a necessidade de reorientar a peça, poupando tempo e recursos. A orientação consistente das dobras também ajuda a manter as ferramentas e a configuração uniformes ao longo do processo de fabrico.
Na indústria são utilizados vários métodos de dobragem, cada um com as suas vantagens e limitações:
Ao compreenderem estes conceitos-chave, os designers e engenheiros podem tomar decisões informadas durante o processo de quinagem, garantindo peças de chapa metálica precisas e de elevada qualidade.
Seguem-se as respostas a algumas perguntas frequentes:
O fator K na flexão de chapas metálicas é um parâmetro crucial que representa a relação entre a distância do eixo neutro e a espessura do material. O eixo neutro é uma linha imaginária dentro do metal que não sofre compressão ou alongamento durante a flexão. Esta posição desloca-se do ponto médio da espessura do material à medida que o metal é dobrado.
A determinação do fator K envolve medições e cálculos. Normalmente, dobra-se amostras do metal e mede-se as principais dimensões, incluindo o raio interior da dobra, a espessura do material e a tolerância da dobra. O fator K pode ser calculado utilizando a fórmula:
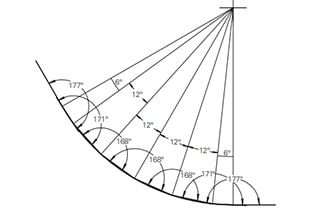
O ângulo de curvatura complementar é (180° - ângulo incluído)
Por conveniência, são frequentemente utilizados gráficos e tabelas de fator K. Estes fornecem valores típicos com base no tipo de material, espessura e método de dobragem. O fator K é influenciado por vários factores, incluindo as propriedades do material, o raio de curvatura, a espessura do material e o método de curvatura utilizado.
Os valores do fator K variam geralmente entre 0,3 e 0,5. Por exemplo, os materiais macios, como o cobre macio, têm um fator K de cerca de 0,35, os materiais semi-duros, como o aço macio e o alumínio, de cerca de 0,41, e os materiais duros, como o bronze e o aço laminado a frio, de cerca de 0,45.
Em aplicações práticas, o fator K é essencial para calcular as tolerâncias e deduções de dobragem, assegurar padrões planos precisos e evitar defeitos durante o processo de dobragem. É frequentemente utilizado em software de projeto e por travão de prensa operadores para o fabrico preciso de chapas metálicas.
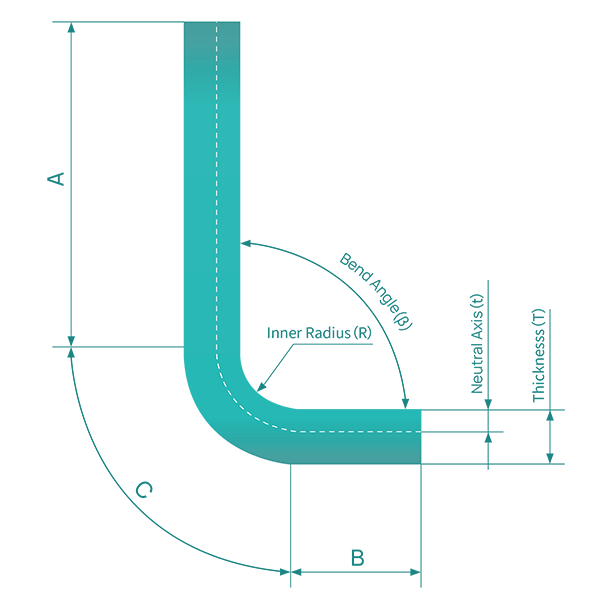
Para calcular a tolerância de dobragem para chapas metálicas, é necessário considerar vários parâmetros-chave e utilizar uma fórmula específica. Os parâmetros necessários são a espessura do material (T), o ângulo de curvatura (A), o raio interior (R) e o fator K (K). A margem de curvatura (BA) é o comprimento do arco da curvatura medido ao longo do eixo neutro da chapa metálica.
A fórmula para calcular o subsídio de curvatura é a seguinte
Onde:
Por exemplo, dado um ângulo de curvatura (A) de 120 graus, um raio interior (R) de 6,5 mm, uma espessura de material (T) de 2,5 mm e um fator K (K) de 0,5, pode calcular a tolerância de curvatura da seguinte forma:
1. Converter o ângulo de curvatura em radianos, se necessário:
2. Aplica os valores à fórmula:
A margem de curvatura (BA) calculada é de 16,23 mm. Este valor é então utilizado para determinar o comprimento plano da chapa metálica necessário para formar a peça de trabalho desejada. O comprimento plano pode ser calculado adicionando os comprimentos das pernas à margem de curvatura. Isto assegura um fabrico preciso e eficiente de peças de chapa metálica.
A tolerância de dobragem (BA) e a dedução de dobragem (BD) são dois conceitos essenciais na dobragem de chapas metálicas que servem diferentes objectivos no processo de fabrico. A tolerância de dobragem refere-se ao comprimento de material necessário para criar uma dobragem, medido ao longo do eixo neutro da chapa metálica. É responsável pelo material efetivamente utilizado na dobragem e é adicionado ao comprimento plano para garantir que as dimensões finais da peça de trabalho cumprem as especificações do projeto.
Por outro lado, a dedução de curvatura representa a quantidade de material que deve ser subtraída do comprimento total do plano para obter a curvatura desejada. Esta dedução é necessária para compensar o efeito de retorno elástico que ocorre quando a força de dobra é removida, assegurando que o ângulo de dobra final é exato e que as dimensões da peça são mantidas.
Em suma, enquanto a tolerância à curvatura é adicionada ao comprimento plano para uma utilização correta do material durante a curvatura, a dedução da curvatura é subtraída para ter em conta o comportamento do material após a curvatura, particularmente a tendência para se desdobrar ligeiramente. Ambos os cálculos são essenciais para obter componentes de chapa metálica precisos e exactos.
O cálculo exato do comprimento plano na dobragem de chapas metálicas é crucial por várias razões que afectam diretamente a qualidade, a eficiência e a relação custo-eficácia do processo de fabrico.
Em primeiro lugar, os cálculos precisos do comprimento plano asseguram que as dimensões finais da peça correspondem às especificações do projeto. Ao contabilizar corretamente a tolerância e a dedução de curvatura, as dimensões da peça acabada serão exactas, assegurando que esta se encaixa corretamente na montagem global e cumpre os requisitos de design pretendidos.
Em segundo lugar, os cálculos exactos do comprimento plano optimizam a utilização e a eficiência do material. Ao determinar o tamanho exato da chapa metálica necessária antes da dobragem, os fabricantes podem minimizar o desperdício e controlar os custos, tornando o processo de fabrico mais eficiente em termos de recursos.
Em terceiro lugar, garantir o comprimento plano correto é vital para o ajuste e montagem adequados das peças. Dimensões incorrectas podem levar a que as peças não se encaixem como pretendido, causando problemas de montagem e potencial retrabalho, o que pode ser dispendioso e demorado.
Em quarto lugar, os cálculos exactos ajudam a manter a distribuição de tensões e a integridade estrutural das peças dobradas. A contabilização correta da tolerância e da dedução de curvatura garante que as peças são curvadas de forma a manter a sua resistência e durabilidade, o que é essencial para a fiabilidade do produto final.
Em quinto lugar, a consistência no fabrico é conseguida através de cálculos precisos do comprimento do plano. Esta consistência reduz os erros e o retrabalho, conduzindo a um processo de fabrico mais eficiente e fiável. Também assegura que cada peça produzida cumpre os mesmos padrões elevados.
Em sexto lugar, os cálculos exactos compensam o efeito de retorno elástico do material, em que a peça dobrada tende a desdobrar-se parcialmente após a remoção da força de dobragem. Ao incorporar a dedução de dobragem correta, os fabricantes podem atingir o ângulo de dobragem pretendido e manter a precisão dimensional após o processo de dobragem.
Por último, o conhecimento das dimensões exactas necessárias para o padrão plano simplifica o processo de fabrico. Permite operações optimizadas, facilitando a produção de componentes dobrados de alta qualidade com o mínimo de esforço e erro.
Em resumo, o cálculo exato do comprimento plano na dobragem de chapas metálicas é essencial para garantir dimensões precisas, otimizar a utilização de materiais, obter um ajuste e montagem adequados, manter a integridade estrutural, garantir a consistência no fabrico, compensar o retorno elástico e simplificar o processo de fabrico.
Nos cálculos de dobragem de chapas metálicas, o impacto dos diferentes tipos de materiais no fator de dobragem é significativo e multifacetado, influenciando a precisão, a qualidade e a eficiência do processo de dobragem. As principais áreas afectadas incluem:
Propriedades do material:
Diferentes materiais apresentam propriedades mecânicas variáveis, como a tensão de cedência, a tensão de rotura e o módulo de elasticidade. Estas propriedades influenciam diretamente o comportamento do material durante a flexão, afectando o fenómeno de retorno elástico e a força de flexão necessária. Por exemplo, os aços de alta resistência requerem normalmente um fator de flexão maior em comparação com os aços macios, devido à sua maior resistência à deformação plástica.
Estrutura de grão e anisotropia:
A estrutura cristalina e a orientação do grão dos metais desempenham um papel crucial no comportamento de flexão. Os materiais com uma estrutura de grão pronunciada, como certas ligas de alumínio, podem apresentar propriedades anisotrópicas, levando a diferentes factores de flexão, dependendo da direção da flexão em relação à orientação do grão. Isto pode resultar num retorno de mola inconsistente e em potenciais defeitos se não for corretamente considerado nos cálculos.
Características de endurecimento por trabalho:
Os materiais com diferentes taxas de endurecimento por trabalho, tais como os aços inoxidáveis austeníticos versus os aços com baixo teor de carbono, requerem abordagens distintas para os cálculos do fator de flexão. O endurecimento por trabalho durante o processo de quinagem pode alterar significativamente as propriedades do material, afectando a forma final e a precisão dimensional.
Coeficientes de expansão térmica:
Para os processos que envolvem calor, como a dobragem a quente ou o tratamento térmico subsequente, o coeficiente de expansão térmica do material torna-se um fator crítico. Os materiais com coeficientes mais elevados podem exigir uma compensação no fator de flexão para ter em conta as alterações dimensionais durante o arrefecimento.
Estado da superfície e tratamentos:
Os tratamentos de superfície, como a anodização, a galvanização ou o endurecimento por cementação, podem alterar as propriedades da superfície do material, afectando o atrito durante a quinagem e alterando potencialmente o fator de quinagem necessário. A presença de camadas de óxido ou revestimentos deve ser considerada em cálculos de flexão precisos.
Variações de espessura:
Embora a espessura do material em si seja um fator chave, a consistência da espessura ao longo da chapa é igualmente importante. Os materiais propensos a variações de espessura, como certas ligas laminadas, podem exigir factores de curvatura adaptáveis ou cálculos mais conservadores para garantir resultados consistentes em toda a peça de trabalho.
Sensibilidade à taxa de deformação:
Alguns materiais, particularmente certas ligas de alumínio e aços de alta resistência, apresentam sensibilidade à taxa de deformação. Isto significa que o fator de flexão pode ter de ser ajustado com base na velocidade da operação de flexão, sendo que uma flexão mais rápida pode exigir cálculos diferentes dos processos mais lentos e controlados.
Estado de tensão residual:
A presença de tensões residuais no material, que podem variar com base no tipo de material e no historial de processamento anterior, pode afetar significativamente o comportamento de flexão. Os materiais com níveis elevados de tensão residual podem exigir tratamentos de alívio de tensão ou factores de flexão ajustados para obter resultados precisos.
Para otimizar as operações de dobragem para diferentes tipos de materiais, é crucial:
Ao considerar cuidadosamente estes impactos específicos do material no fator de dobragem, os fabricantes podem obter uma maior precisão, reduzir as taxas de desperdício e otimizar os seus processos de dobragem de chapa metálica numa vasta gama de materiais.
Como fundador da MachineMFG, dediquei mais de uma década da minha carreira à indústria metalúrgica. A minha vasta experiência permitiu-me tornar-me um especialista nos domínios do fabrico de chapas metálicas, maquinagem, engenharia mecânica e máquinas-ferramentas para metais. Estou constantemente a pensar, a ler e a escrever sobre estes assuntos, esforçando-me constantemente por me manter na vanguarda da minha área. Deixe que os meus conhecimentos e experiência sejam uma mais-valia para a sua empresa.
PT 
EN 
AR 
DE 
ES 
FR 
ID 
IT 
JA 
NL 
PT_BR 
RU 
KO 
TR