Já alguma vez se perguntou porque é que alguns metais dobram na perfeição enquanto outros racham ou deformam? Este artigo mergulha no fascinante mundo da dobragem de chapas metálicas, explorando os factores cruciais que determinam o raio de dobragem ideal. Aprenderá como a espessura do material, a força de dobragem e a seleção da matriz influenciam a dobragem final, garantindo que os seus projectos em metal são perfeitos.
Deverá existir um raio de curvatura para dobragem de chapaO valor do prémio não deve ser demasiado grande ou demasiado pequeno e deve ser escolhido de forma adequada.
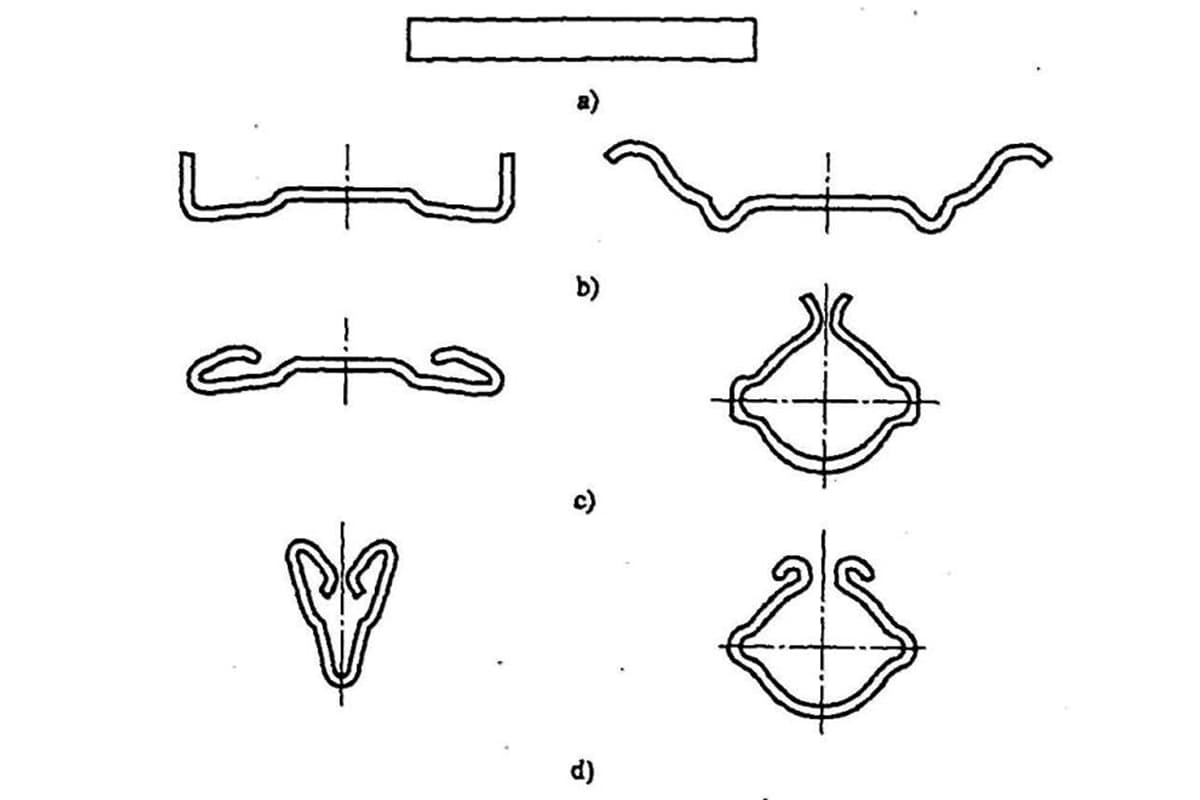
Se o raio de curvatura for demasiado pequeno, provocará fissuras na posição de curvatura;
Se o raio de curvatura for demasiado grande, é fácil rebentar.
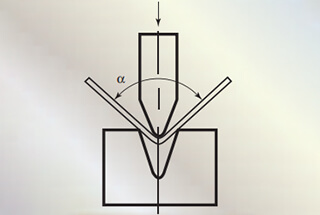
No entanto, é possível utilizar Máquina de ranhurar em V para entalhar primeiro e depois dobrar. Desta forma, obterá um raio de curvatura mais pequeno.
O raio de curvatura ótimo de diferentes espessuras de vários materiais (raio interno de curvatura) ver quadro abaixo:
| Metal | Recozimento Estado | Estado de endurecimento a frio | ||
| A posição correspondente da direção de flexão e da direção da fibra | ||||
| Vertical | Paralelo | Vertical | Paralelo | |
| 08, 10 | 0.1t | 0.4t | 0.4t | 0.8t |
| 15, 20 | 0.1t | 0.5t | 0.5t | 1.0t |
| 25, 30 | 0.2t | 0.6t | 0.6t | 1.2t |
| 45, 50 | 0.5t | 1.0t | 1.0t | 1.7t |
| 65Mn | 1.0t | 2.0t | 2.0t | 3.0t |
| Alumínio | 0.1t | 0.35t | 0.5t | 1.0t |
| Latão | 0.1t | 0.35t | 1.0t | 2.0t |
| Latão macio | 0.1t | 0.35t | 0.35t | 0.8t |
| Latão semirrígido | 0.1t | 0.35t | 0.5t | 1.2t |
| Bronze fosforoso | / | / | 1.0t | 3.0t |
Os dados do quadro acima são os dados preferidos apenas para referência. De facto, os cantos arredondados de travão de prensa são normalmente 0,3, e um pequeno número de cantos arredondados do punção do travão de prensa é 0,5.
Para chapas de aço de baixo carbono comuns, chapas de alumínio antiferrugem, cobre amarelo, cobre roxo, etc., o raio interno de 0,2 não é problema, mas para alguns aço de alto carbonoalumínio duro, alumínio superduro, a utilização de um raio de 0,2 conduzirá a uma fratura por flexão ou a uma fissura no raio exterior.
Quais são os factores que podem afetar o raio de curvatura do chapa metálica?
Existem vários factores que podem afetar o raio de curvatura da chapa metálica, incluindo a espessura do metal, o material de que é feito, o raio do punção superior, a matriz inferior, o força de flexão aplicada, e a temperatura de funcionamento.
Espero que este artigo, baseado na minha experiência pessoal, seja útil para os leitores.
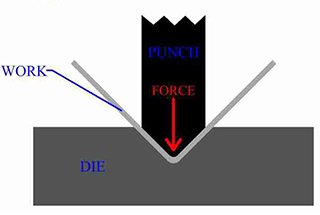
O ângulo de flexão da chapa metálica é o fator chave que afecta a tolerância à flexão.
Por exemplo, se dobrar a chapa metálica com grande raiose o ângulo de curvatura for agudo, será deduzida uma maior margem de curvatura; se o ângulo de curvatura for agudo, será deduzida uma menor margem de curvatura tolerância à flexão serão deduzidos.
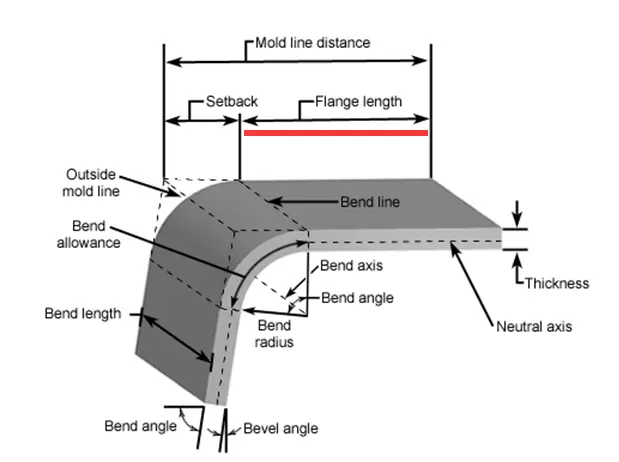
Em aplicações práticas, observou-se que o raio de curvatura aumenta à medida que a espessura do material aumenta.
Estamos cientes de que uma placa mais espessa requer mais força de flexão e uma maior abertura em véu na matriz inferior.
O que afecta então o ângulo de curvatura r?
A tolerância à flexão para chapas da mesma espessura pode variar ligeiramente, o que demonstra que propriedades dos materiais desempenham um papel importante na determinação do raio de curvatura.
A resistência do material à flexão pode influenciar diretamente o raio de flexão.
Embora o material tenha um impacto no raio de curvatura, este tem um efeito limitado na nossa utilização efectiva.
Podemos criar uma tabela de tolerância de dobragem personalizada para diferentes materiais.
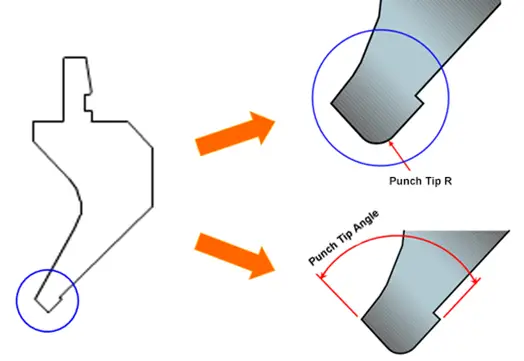
O raio padrão do molde de dobragem não deve exceder r1, e o raio mínimo do punção não deve ser inferior a 1.
Se não existirem requisitos específicos para o raio de curvatura, este terá um impacto limitado no processo de curvatura.
No entanto, para a dobragem de chapa metálica que requer um raio de dobragem específico que seja inferior a 1 ou significativamente superior a 1, não é apenas determinado pelo raio do punção superior.
Por conseguinte, o raio do punção superior afecta diretamente o raio de curvatura final.
É importante ter em conta que, quando o raio da ponta do punção é superior ao raio gerado pela matriz em véu utilizada na dobragem, isso afectará o raio interno do perfil.
Por exemplo:
O raio de curvatura interno será:
Um exemplo típico deste princípio é representado pelos porta-ferramentas de raio que podem ser utilizados para obter curvas de grande raio em pequenas matrizes. Neste caso, o raio interno necessário é produzido pela forma da ponta do punção.
Quando, em vez disso, se pretende reter o raio de curvatura interno produzido pelo
O diâmetro ideal da ponta do punção rdius pode ser calculado com a seguinte equação
Raio ideal da ponta do punção = (R produzido pela matriz) x (2/3)
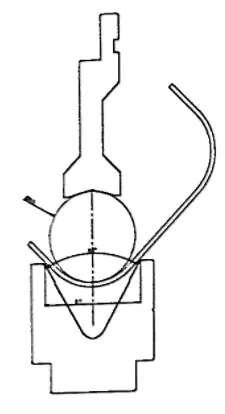
Utilizando esta relação, a superfície do punção é proporcional à força necessária para dobrar a chapa metálica, evitando que a ponta do punção penetre na chapa metálica. Isto evita problemas estéticos ou fissuras no material no interior da dobra.
Além disso, com um raio de ponta demasiado pequeno e com ângulos agudos, é possível que a chapa metálica seja quase cortada e que o perfil se feche sobre o punção, produzindo assim um ângulo diferente do pretendido.
Nem sempre é fácil cumprir a equação acima mencionada devido à falta de diferentes radiadores de ponta de flexão em muitas oficinas.
No entanto, operadores de prensa dobradeira deve utilizar o raio de ponta mais próximo do ideal. Especialmente no caso de chapas grossas, que requerem uma força elevada para serem dobradas, os operadores devem utilizar um raio de ponta de punção adequado para evitar deformações na chapa, problemas dimensionais ou problemas de aparência ou fissuração.
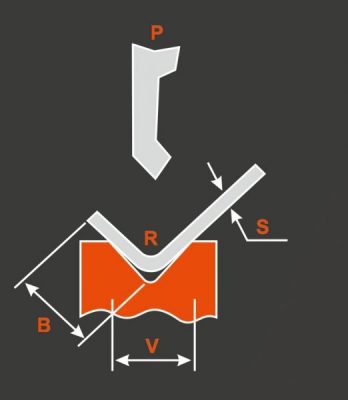
Quanto mais espessa for a chapa metálica, maior é a sua resistência à deformação por flexão.
Por conseguinte, a força de flexão deve ser ajustada em conformidade.
A força de flexão não pode ser aumentada constantemente e deve ser ajustada a um nível adequado.
A força de flexão é diretamente proporcional à espessura da chapa metálica e inversamente proporcional à largura da ranhura inferior da matriz.
Ao dobrar, a espessura da chapa metálica é fixa e a largura da ranhura inferior da matriz é selecionada com base na espessura do metal.
Como resultado, a força de flexão torna-se uma constante, determinada por outros factores.
O raio de curvatura não pode ser determinado com exatidão sem considerar a força de curvatura.
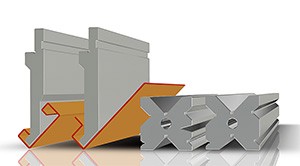
A largura da ranhura inferior da matriz tem uma correlação direta com a espessura da chapa metálica.
Nas aplicações do mundo real, o raio de curvatura aumenta à medida que a espessura do metal aumenta.
Para a mesma espessura de chapa, o raio de curvatura pode também variar em função da largura da abertura em véu.
Por conseguinte, é evidente que a largura da ranhura inferior da matriz desempenha um papel crucial na determinação do raio de curvatura.
Geralmente, a temperatura ambiente de trabalho é a temperatura ambiente, que pode ser ignorada.
A força de flexão contribui para as alterações do raio de flexão, mas é determinada pela espessura da chapa metálica e pela largura da ranhura inferior da matriz.
Todos os factores desempenham um papel na determinação do raio de curvatura e só podem ser limitados com base em requisitos específicos.
Por exemplo, se não existirem requisitos específicos para o raio de curvatura, é adequado limitar todos os factores e utilizar uma tabela de factores de curvatura normalizada.
Se for desejado um raio de curvatura muito maior do que 1, o raio da matriz superior pode ser modificado e pode ser utilizado um fator de curvatura personalizado.
No entanto, não é aconselhável alterar a largura da ranhura inferior da matriz, uma vez que isso terá um impacto tanto no raio de curvatura como na margem de curvatura.
A modificação da largura da ranhura inferior da matriz pode ser utilizada para alterar a margem de curvatura e o raio de curvatura.
Como fundador da MachineMFG, dediquei mais de uma década da minha carreira à indústria metalúrgica. A minha vasta experiência permitiu-me tornar-me um especialista nos domínios do fabrico de chapas metálicas, maquinagem, engenharia mecânica e máquinas-ferramentas para metais. Estou constantemente a pensar, a ler e a escrever sobre estes assuntos, esforçando-me constantemente por me manter na vanguarda da minha área. Deixe que os meus conhecimentos e experiência sejam uma mais-valia para a sua empresa.
PT 
EN 
ES 
FR 
RU 
DE 