Folga óptima entre a parede do orifício flangeado e o bordo de dobragem

Como é que a distância entre a parede de um orifício flangeado e uma aresta de dobragem afecta a integridade de uma peça metálica? Na metalomecânica, esta distância é crucial para evitar danos durante a conformação. Este artigo explora as distâncias mínimas recomendadas e os cálculos para garantir uma dobragem bem sucedida sem comprometer a qualidade da flange. Descubra como determinar o espaçamento ideal com base na espessura do material e noutros parâmetros para um fabrico de metal eficiente e seguro.

Shane
16 de novembro de 2023
Dobragem/dobragem

Índice

1. Peça dobrada com um orifício flangeado (roscado)

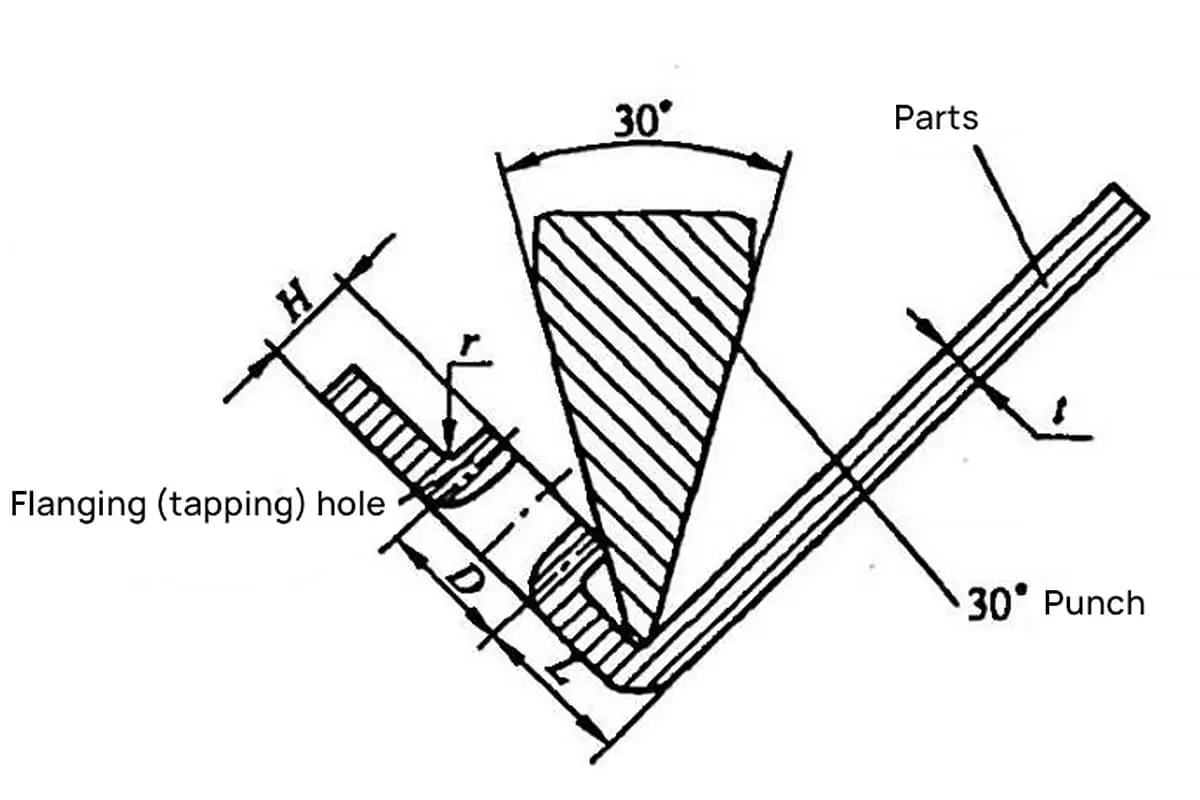
Como mostra a Figura 4-17. O seu orifício flangeado (de rosca)

A distância L entre a parede do furo e a borda da dobra não pode ser demasiado pequena, pois pode danificar o flange (ou mesmo impedir a sua formação).

Figura 4-17 Peça dobrada com um furo flangeado (roscado)

Geralmente, recomenda-se a seleção de L > (7~8)t com base na experiência. Quando o requisito estrutural da peça dobrada requer uma distância mais curta entre a parede do orifício flangeado (roscado) e a borda da dobra, a distância mínima deve ser calculada ou determinada graficamente com base em parâmetros como a espessura do material t, o tamanho do orifício (diâmetro D) do flange (rosca M), a altura do flange, a forma da dobra e raio de curvatura r.

Rosca métrica comum Dimensões da flange com orifício inferior

Consulte a Tabela 4-5 para obter as dimensões do flange do furo inferior da rosca métrica comum. Os exemplos de marcação de dimensões são apresentados na Figura 4-18.

Tabela 4-5 Dimensões comuns da flange de furo inferior com rosca métrica (unidade: mm)

Diâmetro da rosca d	Material Espessura t	Diâmetro interior da flange d₁	Diâmetro exterior da flange D	Altura da flange h	Diâmetro do furo de pré-perfuração d₀	Raio de curvatura r
M2	0. 6	1.6	2. 6 ^+0.16	1.3±0.2	0.8 ±0.1	0.2
	0. 8		2.7^+0.16	1.6±0.2	0.8 ±0.1	0.2
	1		2. 9 ^+0.16	1.8±0.2	1.2 ±0.1	0.4
M2.5	0. 6	2.1	2.9 ^+0.16	1.3±0.2		0.2
	0.8		3. 2^+0.16	1.7±0.2	1.0 ±0.1	0.2
	1.0		3. 5^+0.16	1.9±0.2		0.4
	1.2		3. 5 ^+0.16	2.0 ±0.2	1.2 ±0.1	0.4
M3	0. 8	2.5	3. 6^+0.16	2.0 ±0.2	1.2 ±0.1	0.2
	1.0		3. 6 ^+0.16	2.1 ±0.2		0.4
	1.2		4. 0 ^+0.16	2.2±0.2
	1. 5		4. 2 ^+0.16	2.4±0.2	1.6 ±0.1
M4	1.0	3.3	4.7^+0.16	2.6 ±0.2	1.6 ±0.1	0.4
	1.2		5 ^+0.16	2.8 ±0.2
	1.5		5. 4 ^+0.16	3.0±0.2
	2.0		6 +^0.16	3.2 ±0.2		0.6

Nota: Este quadro é aplicável a flangeamento furos de fundo de rosca de aço de baixo carbono, latão, puro e alumínio. Os dados da tabela são apenas para referência.

A Figura 4-18 mostra um exemplo de anotação de tamanho de flange de furo inferior de rosca métrica.

O Exemplo 4-1 ilustra uma peça dobrada, como mostra a Figura 4-17. A espessura da chapa é t=1,5mm, a rosca M4 é roscada no flange e a altura necessária do flange é H=3,3mm. Calcule a distância mínima entre a parede do furo do flange (rosca) e a borda da dobra.

Solução: Utilizar uma faca de dobragem de 30° para o processamento e o método gráfico para calcular a distância mínima entre a parede do orifício da flange (rosca) e a aresta de dobragem.

A partir do método gráfico, obtemos L=6mm.

2. Distância mínima sugerida entre a parede do orifício da flange (rosca) e o bordo de dobragem

Consulte a Tabela 4-6 para obter as distâncias mínimas geralmente sugeridas entre a parede do orifício da flange (rosca) e o bordo de dobragem.

Tabela 4-6 Distâncias mínimas sugeridas entre a parede do furo da flange (rosca) e o bordo de curvatura (unidade: mm)

Diâmetro da rosca d	Espessura do material t
Diâmetro da rosca d	1.0	1.2	1.5	2.0
M3	4.9	5.1	–	–
M4	–	5.7	6.0	–
M5	–	5.9	6.4	–

Nota: Os dados apresentados no quadro servem de referência. Os valores mínimos não são geralmente utilizados.

Não se esqueçam, partilhar é cuidar! : )

Autor

Shane

Fundador do MachineMFG

Como fundador da MachineMFG, dediquei mais de uma década da minha carreira à indústria metalúrgica. A minha vasta experiência permitiu-me tornar-me um especialista nos domínios do fabrico de chapas metálicas, maquinagem, engenharia mecânica e máquinas-ferramentas para metais. Estou constantemente a pensar, a ler e a escrever sobre estes assuntos, esforçando-me constantemente por me manter na vanguarda da minha área. Deixe que os meus conhecimentos e experiência sejam uma mais-valia para a sua empresa.