Já alguma vez pensou nas forças em jogo quando dobra um tubo? Neste artigo, vamos explorar o fascinante mundo da mecânica de dobragem de tubos. O nosso engenheiro mecânico especialista irá analisar os principais conceitos e cálculos envolvidos, fornecendo informações valiosas tanto para profissionais como para entusiastas. Prepare-se para descobrir a ciência por detrás da criação de curvas suaves e precisas em tubos!
O processo de curvatura de tubos evoluiu significativamente com o surgimento de várias indústrias, como a automóvel, a de motociclos, a de bicicletas e a petroquímica. Este processo é essencial para criar curvas precisas e duradouras nos tubos utilizados nestes sectores.
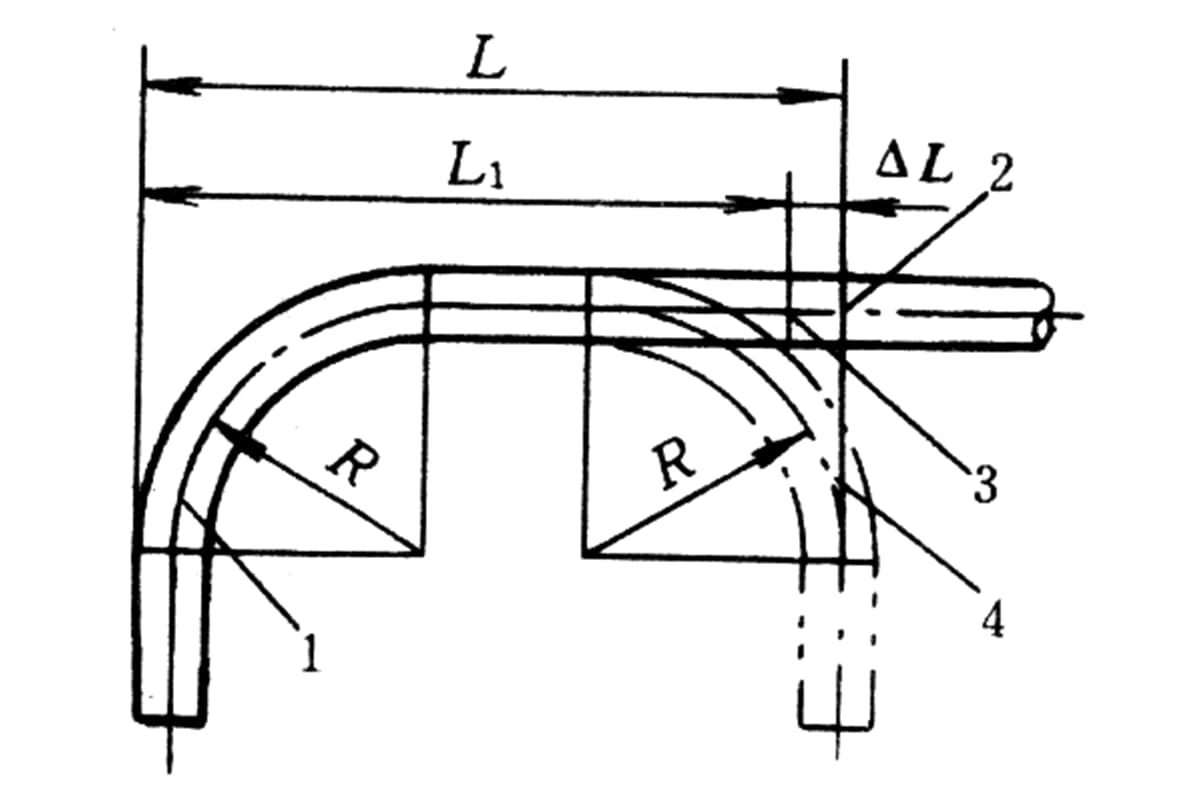
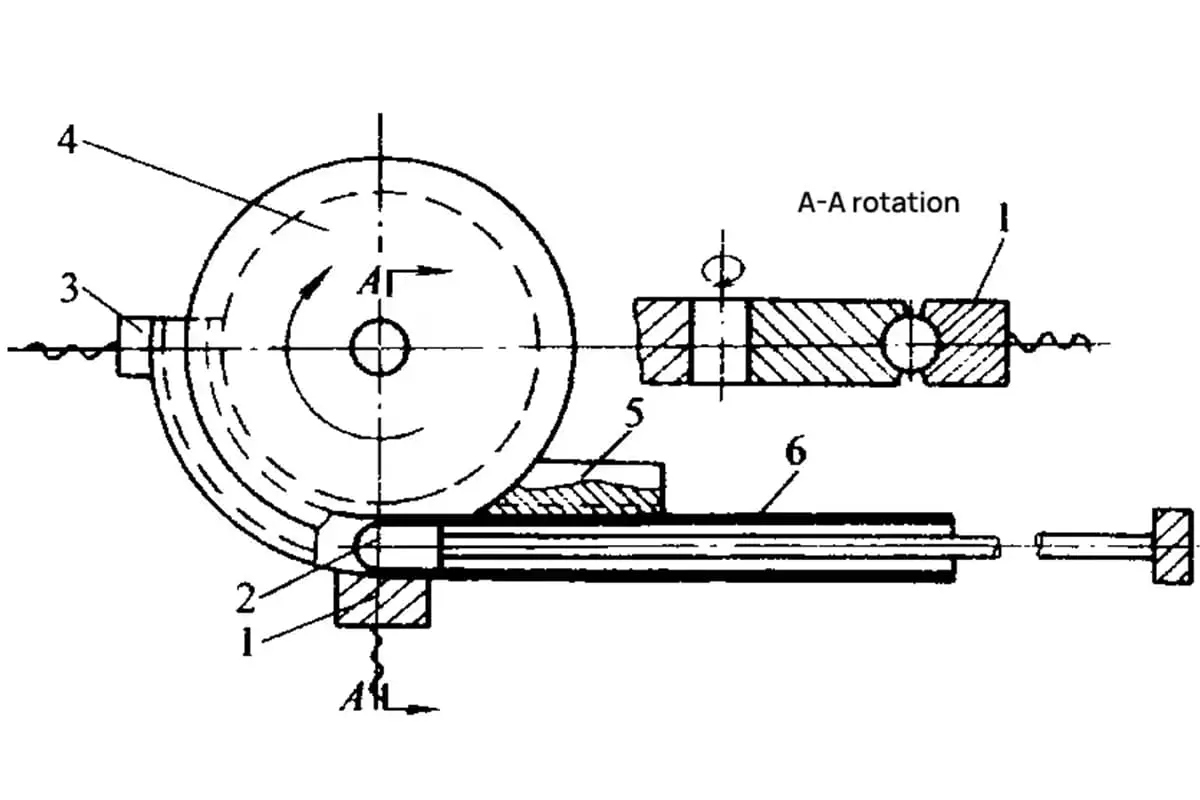
As Figuras 6-19, 6-20, 6-21 e 6-22 representam, respetivamente, os diagramas esquemáticos dos moldes para os dispositivos de enrolamento, empurramento, prensagem e laminagem. Estes diagramas ilustram a configuração específica e os componentes utilizados em cada método de dobragem, fornecendo uma referência visual para a compreensão do processo.
Ao categorizar os métodos de curvatura de tubos com base na técnica de curvatura, temperatura e utilização de enchimentos ou mandris, podemos compreender melhor as aplicações adequadas e as vantagens de cada método. Este conhecimento é crucial para selecionar o processo de curvatura correto para necessidades industriais específicas, garantindo eficiência e precisão no fabrico.

1- Bloco de pressão
2- Haste de núcleo
3- Bloco de fixação
4- Molde de dobragem
5- Bloco antirrugas
6- Tubo Em branco

Coluna de 1 pressão
Manga de 2 guias
3 tubos em branco
Molde de 4 dobras

1-Die
2-Tubo em branco
3-Soco giratório

1 eixo
2,4,6 rolos
Eixo 3-Ativo
5-Tubo de aço
Quando o material do tubo é dobrado, o material no lado exterior da zona de deformação é esticado e alongado pela tensão tangencial, enquanto o material no lado interior é comprimido e encurtado pela compressão tangencial.
Como a tensão tangencial σθ e a deformação εθ são continuamente distribuídos ao longo da secção transversal do material do tubo, podem ser imaginados como semelhantes à flexão do material da placa.
A zona de estiramento no lado exterior transita para a zona de compressão no lado interior, com uma camada neutra na junção.
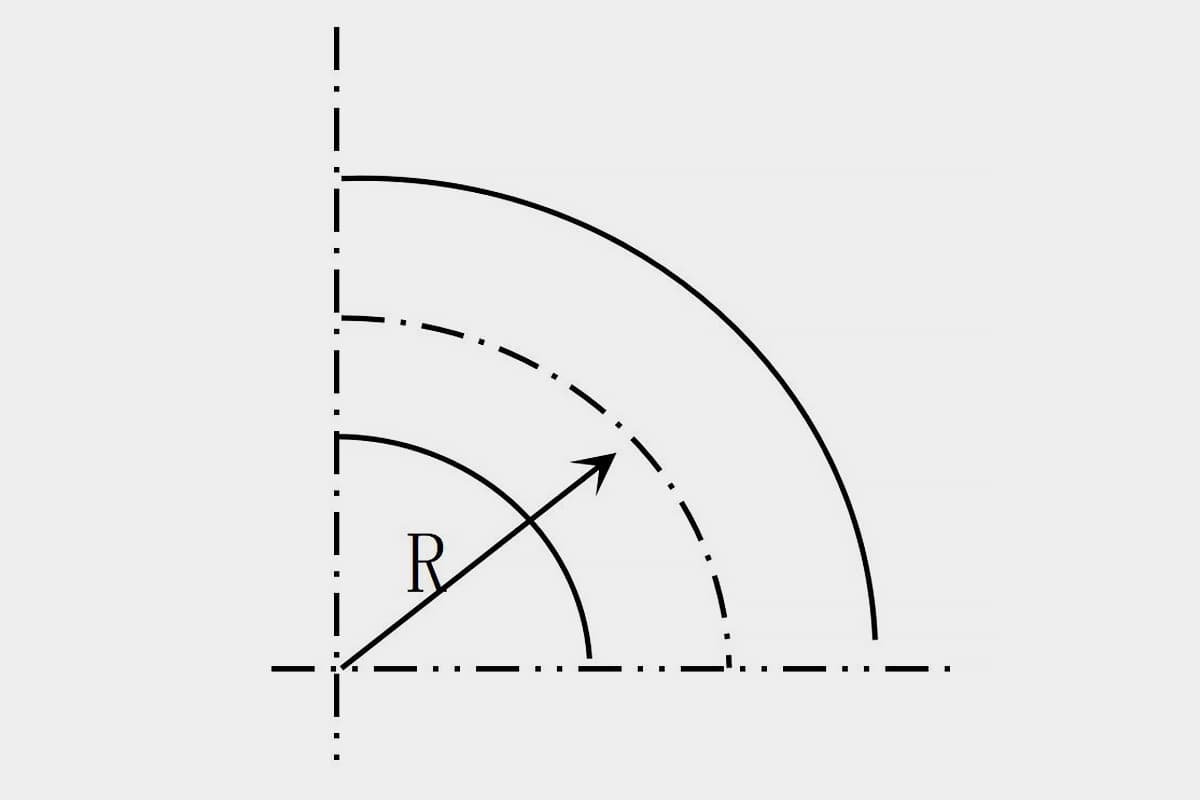
Para simplificar a análise e o cálculo, considera-se geralmente que a camada neutra coincide com a camada central da secção transversal do tubo, e a sua posição na secção transversal pode ser representada pelo raio de curvatura (Figura 6-23).
O grau de deformação por flexão do material do tubo depende da relação raio de curvatura R/D e espessura relativa t/D (R é o raio de curvatura da camada central da secção transversal do tubo, D é o diâmetro exterior do tubo, t é a espessura da parede do tubo).
Quanto mais pequenos forem os valores de R/D e t/D, maior será o grau de deformação por flexão (ou seja, R/D e t/D demasiado pequenos), a parede exterior da camada neutra de flexão tornar-se-á excessivamente fina, podendo mesmo levar à rutura; a parede mais interior do tubo ficará mais espessa, podendo mesmo tornar-se instável e enrugada.
Ao mesmo tempo, com o aumento do grau de deformação, a distorção da secção transversal (achatamento) torna-se mais grave.
Por conseguinte, para garantir a qualidade de conformação do material do tubo, o grau de deformação deve ser controlado dentro dos limites permitidos.
O grau de deformação permitido na flexão de tubos é designado por limite de formação de flexão. O limite de deformação por flexão do material do tubo não depende apenas das propriedades mecânicas do material e do método de flexão, mas também considera os requisitos de utilização dos acessórios para tubos.
Para peças dobradas de uso geral, a tensão máxima de alongamento εmáximo produzida na posição mais afastada da camada neutra no lado exterior da área de deformação por flexão do material do tubo não deve exceder o valor-limite permitido pela plasticidade do material como condição para a definição do limite de enformação.
Ou seja, o raio de curvatura limite rmin que pode ser dobrada no lado interior da peça, desde que a camada da superfície exterior do lado exterior da área de deformação por flexão da peça do tubo não apresente fissuras, é utilizada como limite de formação da flexão da peça do tubo.
rmin está relacionado com as propriedades mecânicas do material, a dimensão estrutural dos acessórios para tubos, o método de processamento da dobragem e outros factores.

a Condições da força
b Condições de tensão-deformação
O mínimo raio de curvatura para diferentes processos de flexão podem ser encontrados na Tabela 6-2.
Tabela 6-2 Raio de curvatura mínimo durante a curvatura do tubo (Unidade: mm)
| Métodos de dobragem | Raio de curvatura mínimo |
| Dobragem por prensa | (3~5)D |
| Dobragem de envoltórios | (2~2.5)D |
| Dobragem de rolos | 6D |
| Flexão por pressão | (2.5~3)D |
Nota: D representa o diâmetro exterior do tubo.
Para o raio de curvatura mínimo de aço e tubos de alumínio, consulte a Tabela 6-3.
Tabela 6-3 Raio de curvatura mínimo de tubos de aço e alumínio (Unidade: mm)
| Diâmetro exterior do tubo | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 |
| Raio de curvatura mínimo | 8 | 12 | 16 | 20 | 28 | 32 | 40 | 45 | 50 | 56 |
| Diâmetro exterior do tubo | 24 | 28 | 30 | 32 | 35 | 38 | 40 | 44 | 48 | 50 |
| Raio de curvatura mínimo | 68 | 84 | 90 | 96 | 105 | 114 | 120 | 132 | 144 | 150 |
Durante a curvatura do tubo, a distorção da forma da secção transversal é inevitável.
O material no lado exterior da camada neutra sofre uma tensão tangencial de tração, afinando a parede do tubo; o material no lado interior da camada neutra sofre uma tensão tangencial de compressão, engrossando a parede do tubo.
O material nos lados mais externo e interno da área de deformação por flexão sofre a maior tensão tangencial, portanto, as maiores mudanças na espessura da parede do tubo ocorrem lá (Fig. 6-24).
Na flexão com enchimentos ou hastes de núcleo, a secção transversal é basicamente capaz de manter uma forma circular, mas a espessura da parede muda. Na flexão sem suporte flexão livreSe a secção transversal do tubo for circular, a secção transversal do tubo torna-se elíptica (Fig. 6-24a, b).
Além disso, à medida que o grau de deformação por flexão aumenta (isto é, o raio de flexão diminui), a aresta interior torna-se instável e enruga-se. No caso de tubos quadrados em flexão suportada (Fig. 6-24c, d), a secção transversal muda para uma forma trapezoidal.

A elipticidade é frequentemente utilizada na produção para medir as alterações na secção transversal circular de um tubo.
Elipticidade= Dmáximo-Dmin/D ×100% (6-21)
Neste fórmulaDmax é a dimensão máxima do diâmetro exterior medida em qualquer direção da mesma secção transversal do tubo depois de dobrado, e Dmin é a dimensão mínima do diâmetro exterior medida em qualquer direção da mesma secção transversal do tubo depois de dobrado.
A Figura 6-25 é um gráfico de elipticidade, que representa a mudança de elipticidade correspondente à curvatura adimensional R0/R (R0 é o raio exterior do tubo, R é o raio de curvatura da camada central da secção de flexão) numa coordenada logarítmica, representada como uma família de linhas rectas com a relação t/R0 como variável de parâmetro.
Como se pode ver na figura, quanto maior for o grau de flexão, maior será a elipticidade da secção transversal.
Por isso, a elipticidade é frequentemente utilizada na produção como um índice importante para inspecionar a qualidade dos tubos dobrados. Dependendo dos diferentes desempenhos de utilização dos materiais dos tubos curvados, os requisitos para a sua elipticidade também variam.
Por exemplo, para componentes de tubos dobrados utilizados em projectos de condutas industriais, o tubo de alta pressão não excede 5%; os tubos de média e baixa pressão são 8%; os tubos de alumínio são 9%; e os tubos de liga de cobre e de liga de alumínio são 8%.

A distorção da forma da secção pode reduzir a área da secção transversal, aumentando a resistência ao fluxo de fluido, e pode também afetar o desempenho funcional do tubo na estrutura.
Por conseguinte, no processo de curvatura do tubo, devem ser tomadas medidas para controlar a distorção dentro dos limites exigidos.
Os métodos eficazes para evitar a distorção da forma da secção transversal são:
1) Apoiar a secção transversal com um mandril na zona de deformação por flexão para evitar a distorção da secção transversal.
Para diferentes processos de dobragem, devem ser utilizados diferentes tipos de mandris. Os mandris rígidos são frequentemente utilizados na dobragem e no enrolamento, e a cabeça do mandril é hemisférica ou tem outra forma de superfície curva.
A Figura 6-26 e a Figura 6-27 permitem determinar se é necessário um mandril durante a dobragem e qual o tipo de mandril a utilizar.

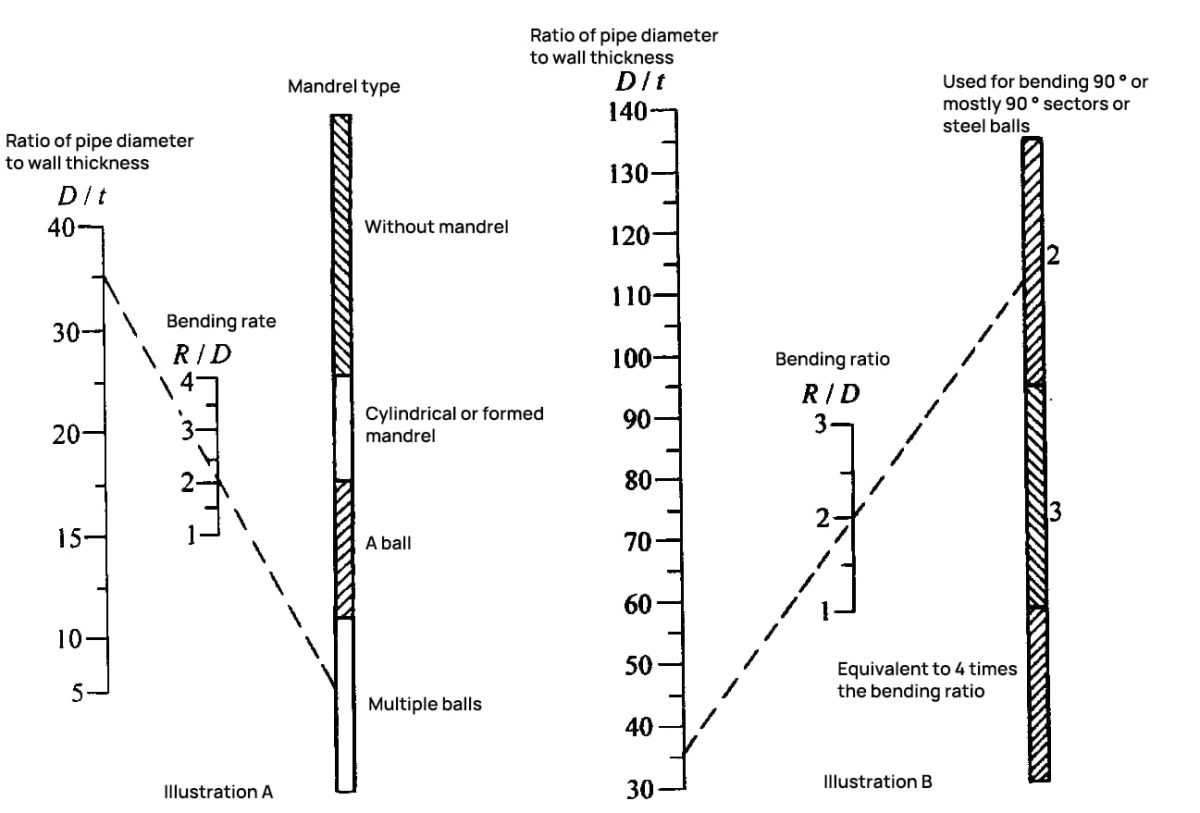
2) O enchimento do tubo curvo com meios granulares, meios fluidos, meios elásticos ou ligas de baixo ponto de fusão também pode substituir a haste central para evitar a distorção da forma da secção. Este método é relativamente fácil de aplicar e é amplamente utilizado, principalmente para produção em pequena e média escala.
3) Na superfície do molde em contacto com o material do tubo, uma ranhura é feita para corresponder à forma da secção do material do tubo, reduzindo a pressão na superfície de contacto e impedindo a distorção da secção. Esta é uma medida bastante eficaz para evitar a distorção da forma da secção.
4) O método de utilização do método de contra-deformação para controlar a alteração da secção do tubo (Figura 6-28) é frequentemente utilizado no processo de curvatura sem núcleo no dobrador de tubos. A caraterística deste método é a sua estrutura simples, pelo que é amplamente utilizado.
A utilização da contra-deformação para a dobragem sem núcleo significa que o tubo em branco recebe antecipadamente uma certa quantidade de deformação inversa. Depois, após a dobragem, a deformação em diferentes direcções anula-se mutuamente, mantendo basicamente a secção do tubo em branco circular para cumprir os requisitos de elipticidade, garantindo assim a qualidade do tubo dobrado.

1-Molde de dobragem
2-Bloco de aperto
3 rolos
Roda de 4 guias
5-Pipe Blank
A forma da secção transversal da ranhura anti-deformação, como mostra a Figura 6-29, o tamanho da ranhura anti-deformação está relacionado com o raio de curvatura relativo (o raio de curvatura da camada central, o diâmetro exterior do tubo). Ver Tabela 6-4.
Tabela 6-4 Dimensões da ranhura anti-deformação
| Raio de curvatura relativo R/D | R1 | R2 | R3 | H |
| 1.5~2 | 0.5D | 0.95D | 0.37D | 0.56D |
| >2~3.5 | 0.5D | 1.0D | 0.4D | 0.545D |
| ≥3.5 | 0.5D | - | 0.5D | 0.5D |

1-Molde de dobragem
2-Rolo anti-deformação
A alteração da espessura do tubo depende principalmente do raio de curvatura relativo R/D e da espessura relativa t/D. Na produção, a espessura mínima da parede tmin no exterior de flexão e a espessura máxima da parede tmáximo no interior pode normalmente ser estimado utilizando a seguinte fórmula:

Na fórmula,
O adelgaçamento do material do tubo reduz a resistência mecânica e a capacidade de utilização dos acessórios. Por conseguinte, na produção, a taxa de adelgaçamento da parede é frequentemente utilizada como um índice técnico para medir a alteração da espessura da parede, a fim de satisfazer a capacidade de utilização dos acessórios.
Taxa de adelgaçamento da parede do tubo = t-tmin/t×100%
Na fórmula:
O desempenho dos materiais dos tubos varia, e existem diferentes requisitos para a taxa de redução da espessura da parede.
Por exemplo, para os acessórios de tubagem utilizados na engenharia de tubagens industriais, o tubo de alta pressão não excede 10%; o tubo de média e baixa pressão não excede 15% e não é inferior à espessura de parede calculada no projeto.
As medidas para reduzir o afinamento da espessura dos tubos incluem:
1) Reduzir o valor numérico da tensão de tração gerada no exterior da camada neutra. Por exemplo, utilizando o método de aquecimento local por resistência para reduzir a resistência à deformação da material metálico dentro da camada neutra, fazendo com que a deformação se concentre mais na parte comprimida, atingindo o objetivo de reduzir o nível de tensão da parte em tração.
2) Alterar o estado de tensão da zona de deformação e aumentar a componente de tensão de compressão. Por exemplo, a mudança de flexão para empurrão pode superar fundamentalmente o defeito de desbaste excessivo da parede do tubo.
O cálculo do binário de flexão do material do tubo é a base para determinar os parâmetros de energia do curvador de tubos.
De acordo com a análise da teoria da mecânica dos plásticos, a expressão teórica do momento fletor quando o material do tubo é uniformemente dobrado é derivada da seguinte forma
Binário de flexão do material do tubo:
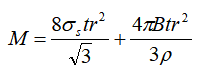
Na fórmula:
O momento de flexão real do material do tubo não só depende das propriedades do material do tubo, da forma e tamanho da secção transversal, do raio de flexão e de outros parâmetros, como também está muito relacionado com o método de flexão e a estrutura do molde utilizado.
Por conseguinte, é atualmente impossível representar todos estes factores através de uma fórmula de cálculo, sendo apenas possível fazer estimativas na produção.
O binário de flexão do material do tubo pode ser estimado com a seguinte fórmula:

Na equação,
O coeficiente µ não é o coeficiente de atrito; o seu valor depende do estado da superfície do tubo, do método de curvatura, especialmente se é utilizado um mandril, do tipo e da forma do mandril, e até de vários factores relacionados com a posição do mandril.
De um modo geral, quando um mandril rígido é utilizado sem lubrificação, pode ser adotado um valor de 5 a 8; quando é utilizado um mandril rígido articulado, pode ser adotado um valor de µ=3.
A forma da secção transversal da ranhura anti-deformação é mostrada na Figura 6-29.
As dimensões da ranhura anti-deformação estão relacionadas com o raio de curvatura relativo (o raio de curvatura da camada central, o diâmetro exterior do tubo).
Ver Quadro 6-4.
Tabela 6-4 Dimensões da ranhura anti-deformação
| Raio de curvatura relativo R/D | R1 | R2 | R3 | H |
| 1.5~2 | 0.5D | 0.95D | 0.37D | 0.56D |
| >2~3.5 | 0.5D | 1.0D | 0.4D | 0.545D |
| ≥3.5 | 0.5D | - | 0.5D | 0.5D |

1-Molde de dobragem
2-Rolo anti-deformação
A alteração da espessura do tubo depende principalmente do raio de curvatura relativo R/D e da espessura relativa t/D.
Na produção, a espessura mínima da parede tmin no lado exterior da curva e a espessura máxima da parede tmáximo no lado interior pode geralmente ser estimado utilizando a seguinte fórmula:

Na fórmula:
O desbaste do material do tubo reduz a resistência mecânica e o desempenho dos acessórios para tubos. Por conseguinte, a taxa de desbaste é frequentemente utilizada na produção como um indicador técnico para medir a alteração da espessura da parede, de modo a cumprir os requisitos de desempenho dos acessórios para tubos.
Taxa de adelgaçamento da parede do tubo = (t-tmin)/t×100%
Na fórmula:
Diferentes desempenhos do material do tubo requerem diferentes taxas de desbaste. Por exemplo, para os acessórios de tubagem utilizados na engenharia de condutas industriais, o tubo de alta pressão não deve exceder 10%; os tubos de média e baixa pressão não devem exceder 15% e não devem ser inferiores à espessura da parede de cálculo do projeto.
As medidas para reduzir o afinamento da espessura do tubo incluem:
1) Reduzir o valor numérico da tensão de tração gerada no lado exterior da camada neutra, como a adoção do método de aquecimento local por resistência, reduzindo a resistência à deformação do material metálico no lado interior da camada neutra, tornando a deformação mais concentrada na parte comprimida, atingindo assim o objetivo de reduzir o nível de tensão da parte de tração.
2) Alterar o estado de tensão da zona de deformação e aumentar a componente de tensão de compressão. Por exemplo, a mudança da flexão para o empurrão pode ultrapassar fundamentalmente o defeito de desbaste excessivo da parede do tubo.
O cálculo do binário de flexão do tubo é a base para determinar os parâmetros de potência do curvador de tubos. De acordo com a análise da teoria da mecânica plástica, a expressão teórica do momento de flexão uniforme do tubo é derivada da seguinte forma:
Binário de flexão do tubo:

Na fórmula:
O momento de flexão real do material do tubo não só depende do desempenho do material do tubo, da forma e tamanho da secção transversal, do raio de flexão e de outros parâmetros, mas também tem muito a ver com o método de flexão e a estrutura do molde utilizado.
Por conseguinte, é atualmente impossível exprimir todos os factores numa fórmula de cálculo, sendo apenas possível fazer estimativas na produção.
O momento de flexão do material do tubo pode ser estimado com a seguinte fórmula:

Na fórmula:
O coeficiente não é o coeficiente de atrito µ, o seu valor depende do estado da superfície do tubo, do método de curvatura e, especialmente, da utilização ou não de um mandril, do tipo e da forma do mandril e até de vários factores relacionados com a posição do mandril.
De um modo geral, quando um mandril rígido é utilizado sem lubrificação, pode ser considerado como =5 a 8; se for utilizado um mandril rígido articulado, pode ser considerado como µ=3.
A conformação por laminagem de tubos é um processo de conformação especial desenvolvido a partir de estampagem processos de flangeamento e estrangulamento. É um processo de deformação em que o bordo da boca do tubo é dobrado localmente através da aplicação de pressão axial à peça de tubo através do molde.
A utilização desta tecnologia para o fabrico de peças apresenta uma série de vantagens, tais como uma tecnologia simples, menos processos, baixo custo e boa qualidade. Pode mesmo produzir peças que são difíceis de obter com outros métodos de estampagem.
Este processo tem sido amplamente utilizado em vários domínios industriais, como o automóvel e o aeroespacial.
Existem duas formas básicas de moldagem por torneamento de tubos, nomeadamente o rolo exterior e o rolo interior (Figura 6-30).

a, b rolo exterior;
c, d rolo para dentro
1-Tubo em branco
2-Anel guia de fluxo
Molde de 3 cones
4-Molde de bordo redondo
Rolo exterior: O tubo em bruto é virado de dentro para fora sob pressão axial, aumentando a sua circunferência após a conformação.
Rolo para dentro: O tubo em bruto é enrolado de fora para dentro, reduzindo a sua circunferência após a formação.
O processo de laminagem pode não só formar eficazmente vários tipos de peças tubulares de parede dupla ou multicamadas, mas também processar copos de fundo convexo, tubos escalonados, tubos de forma especial, bem como tubos semi-duplos, cilindros anulares de parede dupla, porcas ocas de parede dupla, permutadores de calor, silenciadores de automóveis, tubos de guia de ondas na indústria eletrónica, etc.
Atualmente, estas peças são geralmente processadas por estampagem em várias etapas e métodos de soldaduraque são difíceis, dispendiosas e de fraca qualidade visual.
A utilização do processo de laminagem garante a fiabilidade da peça, a leveza e a poupança de matérias-primas.

Atualmente, de acordo com os dados, muitos materiais metálicos podem ser formados no molde em vários métodos de laminagem diferentes, tais como liga de alumínio, cobre e ligas de cobre, aço de baixo carbono, aço inoxidável austenítico, etc. Os tubos em bruto de todas as especificações sonoras podem ser laminados com êxito em tubos de camada dupla.
A perfilagem, comparada com outras processos de conformaçãoO processo de deformação é mais complexo e inclui o alargamento, a ondulação, a laminagem e a sua conversão mútua.
Existem vários moldes para realizar este processo de conformação, entre os quais os mais simples e mais utilizados são os moldes cónicos e os moldes de filete.
1. Molde de laminação de tubo cónico
A estrutura do molde de laminação do tubo cónico é mostrada na Figura 6-32. Esta estrutura do molde é simples, e podem ser formados diferentes especificações de tubos num conjunto de moldes, o que é difícil de conseguir noutros moldes de formação de tubos.
Além disso, como um processo de pré-formação para a formação de rolos de tubos de precisão, a formação de moldes cónicos é amplamente utilizada.

uma estrutura de molde de inversão de tubo
b Parâmetros do processo de inversão do tubo cónico
1 - Cabeça de prensa
2 - Tubo de tarugo
3 - Molde de cone
Durante o processo de torneamento do tubo, uma extremidade do tubo em bruto é colocada numa matriz cónica, enquanto a outra extremidade é sujeita à pressão axial da prensa deslizante para conseguir o torneamento do tubo em bruto.
Ao conceber este tipo de matrizo ângulo de meio cone α da matriz é o parâmetro mais crítico.
A dimensão de α não só determina a viabilidade do torneamento do tubo, como também afecta as dimensões geométricas do torneamento do tubo, ou seja, o coeficiente de torneamento do tubo K (K=D/D1, em que D e D1 são o diâmetro exterior do tubo em bruto e o diâmetro exterior do tubo torneado, respetivamente).
Obviamente, existe um ângulo crítico de meio-cone α0, e a viragem só pode ser efectuada normalmente quando o ângulo de meio-cone α≥ α0.
µ, H, Golubnov derivado com base no princípio da tensão principal:

Tendo em conta a influência do reforço do material e a rigidez da extremidade alargada, a fórmula acima pode ser modificada do seguinte modo

Na fórmula:

Para um tubo de alumínio 3A21 de 42 mm, calculado pela fórmula acima, o ângulo é de 55° - 60°.
Os testes empíricos mostram que, quando o ângulo é α≥60° (α≈68°), a inversão do tubo pode ocorrer sem problemas. Neste momento, a pressão axial é a mais pequena.
Quando o ângulo é de 55° - 60°, a extremidade do tubo em branco enrola-se mas não entra na fase de inversão. Quando o ângulo é α<55°, a extremidade do tubo apenas se alarga na matriz cónica e não se enrola.
Durante a inversão do molde do cone, a extremidade do tubo desliza facilmente, fazendo com que a parte invertida do tubo fique fora do eixo com o molde original do tubo e causando uma flexão axial durante a inversão.
É difícil obter uma peça de tubo invertido de camada dupla que cumpra os requisitos de qualidade da montagem. Por isso, um redondo O molde de inversão de cantos foi desenvolvido com base no molde de cone.
2. Molde para virar com cantos redondos
A matriz de inversão de cantos redondos utiliza a parte de trabalho da matriz, que é um círculo de raio, para forçar a extremidade do tubo comprimido axialmente a deformar-se ao longo do seu arco para conseguir a inversão do tubo.
A Figura 6-33 mostra um diagrama esquemático de um tubo em bruto com uma espessura de t e um diâmetro médio de D, laminado num molde de canto redondo com um raio de r, sob carga axial, a extremidade do tubo enrola-se para cima ao longo do arco do molde para obter uma peça de tubo laminado com um diâmetro de D1.
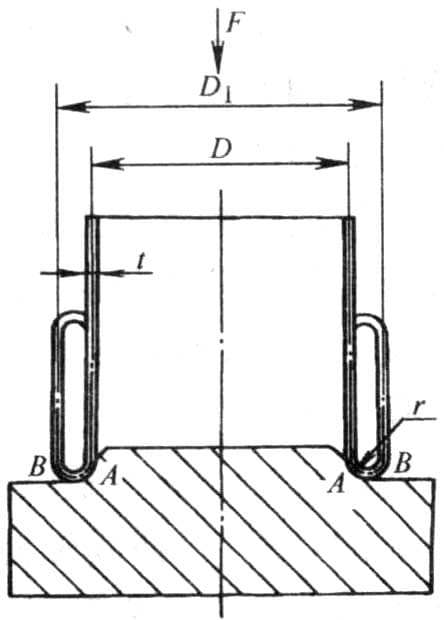
O parâmetro mais importante na conceção de uma matriz de flangeamento de canto redondo é o raio r do canto da matriz. Ele determina não só as dimensões geométricas da peça flangeada, mas também influencia a magnitude da força de flangeamento.
Para o 3A21 recozido tubo de alumínio do tipo Φ41×1, tanto a análise teórica como os resultados experimentais mostram que o raio crítico do filete da matriz (raio mínimo do filete) para a instabilidade da inversão do tubo é de cerca de 2 mm; o raio ótimo do filete é de aproximadamente 3 mm; o raio máximo do filete é de cerca de 4 mm.
Isto indica que a estabilidade e a qualidade da inversão do tubo sob carga axial dependem do raio de filete da matriz r. Se r for inferior a um determinado valor crítico, a extremidade do tubo não se enrola ao longo do arco da matriz; quando r é demasiado grande, a extremidade do tubo fracturase e não pode ser invertida com êxito. Só quando r está dentro de um intervalo adequado é que a inversão do tubo pode ser efectuada.
Semelhante à curvatura para fora do material do tubo, a curvatura para dentro do tubo também pode ser efectuada no molde em cone e no molde de filete (Figura 6-34).
Em comparação com outros processos de conformação, é propenso à instabilidade. Porque durante a ondulação para dentro, o diâmetro do tubo diminui após a deformação, a parede do tubo engrossa, a força de inversão do tubo aumenta, o que traz dificuldades à formação da ondulação.
De acordo com cálculos teóricos e prática, quando o ângulo crítico do semi-cone β do molde do cone de inversão do tubo é ≥120°, o processo de enrolamento pode prosseguir suavemente. Na produção, o valor é geralmente tomado como β≥120°~125°, rp≈4mm.
O processo de enrolamento do tubo só pode ocorrer quando a carga necessária para o enrolamento é inferior ao limite de instabilidade axial. Uma vez que a carga de formação de enrolamento depende em grande parte dos parâmetros geométricos do molde, em termos de molde de filete, depende do raio de filete r.
Por conseguinte, é possível determinar uma região viável para a formação de enrolamentos (Figura 6-35).

um molde cónico
b Cunho arredondado

A partir da Figura 6-35, pode ver-se que a área de laminagem interna é bastante pequena e a carga de laminagem é numericamente superior à da laminagem externa, atingindo quase 50%.
Os dados existentes mostram que, tanto a nível nacional como internacional, os parâmetros óptimos do processo de laminagem externa foram estudados teórica e praticamente, e foi descoberta a relação entre a tensão de compressão axial mínima necessária para uma laminagem completa e o diâmetro interior, o diâmetro exterior e a espessura da parede do material tubular.
Durante a laminagem externa de materiais tubulares, a alteração da espessura da parede não é significativa.
No entanto, durante a laminagem interna, a tensão de compressão circunferencial faz com que a espessura da parede no filete do molde aumente continuamente até atingir um valor constante, que pode ser 1,5 vezes a espessura original. Portanto, para completar a laminação interna, é necessária uma carga axial maior.
Nos dois tipos de laminagem acima referidos (laminagem tradicional), existem algumas deficiências:
1. O início da segunda camada da parede do tubo não é paralelo à parede original do tubo, mas vira sempre na direção da cavidade interior do tubo de parede dupla;
2. Existe uma certa distância entre a parede do novo tubo e a parede do tubo original, que depende do diâmetro relativo (D/t) do material do tubo original;
3. Na laminagem interna, a segunda camada da parede do tubo é consideravelmente mais espessa, o que, por sua vez, conduz a um aumento da pressão axial durante a laminagem.
Os problemas que surgem nos processos acima mencionados devem-se ao mecanismo de conformação, que limita a forma geométrica dos tubos obtidos, especialmente a fraca estabilidade e a elevada dificuldade do processo de laminagem interna, que precisa de ser melhorado.
Por conseguinte, surgiu o método de formação de rolos de tensão de tração para a laminagem interna de materiais tubulares.
A caraterística do método de formação por laminagem sob tensão de tração é que interrompe a laminagem na primeira fase de laminagem interna do material tubular e confere à extremidade laminada uma curvatura inversa, direccionando-a para o exterior da cavidade.
Em seguida, através da ação do molde convexo, a força de tração que actua na aresta de curvatura inversa na parede interior faz com que o tubo em bruto sofra um rolamento interno, em vez de rolar pela pressão axial que actua na parede exterior, reduzindo assim a sua pressão axial.
Este processo permite obter uma maior altura da parede interior, uma espessura de parede constante e uma maior precisão do produto.
O método de perfilagem por tensão de tração expandiu a gama de aplicações do processo de perfilagem interna, como a produção de juntas de tubos, assentos de rolamentos e outros (Figura 6-36).

O método de perfilagem por tensão de tração pode ser dividido em três etapas, como se mostra na Figura 6-37.
Na primeira etapa (Figura 6-37a), a laminação interna tradicional termina quando a borda do tubo deixa um quarto da matriz de filete.
Neste momento, a distância entre a borda do tubo e a parede interna da matriz formará o suporte radial do produto final e deve ser igual à largura necessária.
Na segunda etapa (Figura 6-37b), a matriz convexa de fundo plano desce, forçando o bordo do tubo a flangear (semelhante à flangeamento de furos da placa). A distância entre a matriz convexa e a matriz do rolo interior é determinada pela espessura da parede do tubo (a espessura da parede do rolo interior do tubo é ligeiramente aumentada).
Na terceira etapa (Figura 6-37c, d), a matriz convexa de formação sobe, fazendo com que a borda do tubo role para dentro, gerando assim a segunda camada de parede do tubo sob o impulso da matriz convexa de formação.
Como se pode ver na figura, a matriz convexa de formação actua no bordo do tubo com tensão de tração e não com tensão de compressão que actua em todo o tubo.
Não há deslizamento relativo entre a matriz e o material deformado, e é mantida uma distância entre as cargas de formação, reduzindo assim a tensão de compressão axial na área de transmissão do tubo, evitando assim a instabilidade.
Por conseguinte, a laminagem por tração tem maior liberdade na escolha do raio de laminagem, enquanto o raio da matriz é um parâmetro de processo importante nos processos de maquinagem tradicionais (Figura 6-35).

Condições para a execução bem sucedida deste processo:
FFuro de perfuração≥FRolamento (6-22)
A força de perfuração inclui três componentes (símbolo na Figura 6-37d): a carga que causa a deformação plástica do material no raio rP; a carga necessária para superar o atrito no canto ra entre o punção e a borda do tubo; a carga necessária para dobrar e desdobrar o material da borda da posição radial para a axial.
Na expressão analítica, σ1 é utilizado para representar a tensão de deformação da parede interna.
Então,

A perfilagem inclui dois aspectos: a carga necessária para a laminagem do material para diferentes posições de raios de curvatura e a carga necessária para a flexão e o ressalto desde o início até ao fim da zona de deformação.
Na análise, σ0 é utilizado para representar a tensão de deformação da parede exterior, e σm representa a tensão média de deformação plástica na zona de deformação.

Conclusão:
O método de formação do tubo por laminagem sob tensão de tração foi comprovado através de experiências.
Embora sejam necessárias duas fases de preparação antes do início da laminagem e o recozimento de recristalização seja necessário quando necessário, tem as seguintes vantagens em comparação com o processo de laminagem tradicional:
1) O bordo laminado vira para o centro da cavidade, facilitando a coordenação com outras peças, como a bola rolamento assentos.
2) A carga de rolamento é significativamente reduzida.
3) O limite de conformação é muito melhorado, e os produtos com um raio de rolamento mais pequeno pode ser obtido.
4) Não há fricção e não há necessidade de lubrificação.
5) A espessura da parede interna é aproximadamente igual à espessura da parede externa, e apenas a borda sob carga é ligeiramente mais espessa (Figura 6-38).
As condições experimentais da peça mostrada na Figura 6-38 são as seguintes:
O tubo é fabricado em aço de baixo carbono, Dfora = 90mm, t0= 2,4mm, H =150mm.
O diâmetro do molde côncavo (Figura 6-37d) é Dd = 97mm.
O diâmetro da matriz convexa (Figura 6-37d) é Dp =72mm.
6) Devido à ausência de fricção e ao duplo constrangimento das matrizes convexas e côncavas na parede da peça, a peça tem uma elevada precisão dimensional (Figura 6-37d).
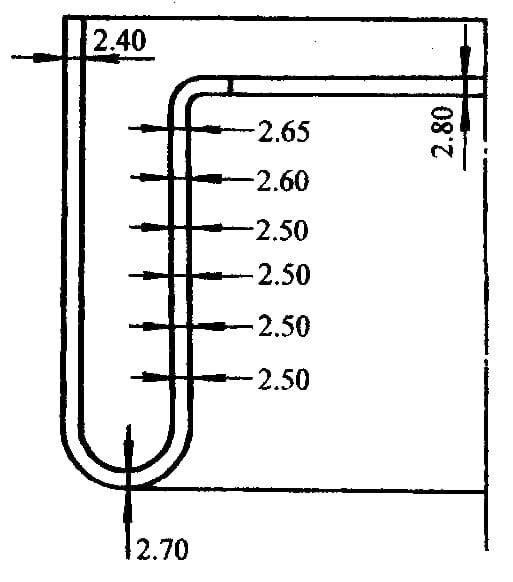
Figura 6-37 Processo de enformação por rolo com tensão de tração (processo de enformação interior melhorado)
Condições para o êxito da aplicação deste processo:
FFuro de perfuração≥FRolamento (6-22)
O força de perfuração inclui três itens (símbolo na Figura 6-37d): a carga que causa a deformação plástica do material no raio rp; a carga necessária para superar a força de atrito entre o canto do punção em ra e a borda do tubo; a carga necessária para a flexão e flexão reversa do material da borda da posição radial para a posição axial.
Na expressão analítica, σ1 representa a tensão de deformação da parede interior.

A perfilagem inclui dois aspectos: a carga necessária para o material rolar para diferentes posições de raio (curvatura) e a carga necessária para dobrar e reverter a dobragem do início ao fim da área de deformação.
Na análise, σ0 é utilizado para representar a tensão de deformação da parede exterior, e σm é utilizado para representar a tensão média de deformação plástica na área de deformação.

Conclusão:
O método de formação de materiais para tubos por laminagem sob tensão foi comprovado por experiências. Embora sejam necessárias duas fases de preparação antes do início da laminagem e o recozimento de recristalização seja necessário quando necessário, apresenta as seguintes vantagens em relação aos processos de laminagem tradicionais:
1) O bordo laminado gira em direção ao centro da cavidade, facilitando a cooperação com outras peças, tais como assentos de rolamentos de esferas.
2) A carga de rolamento é muito reduzida.
3) O limite de conformação é muito melhorado, e os produtos com raios de laminação mais pequenos pode ser obtido.
4) Não há fricção e não há necessidade de lubrificação.
5) A espessura da parede interior é aproximadamente igual à da parede exterior, e apenas os bordos sob carga são ligeiramente mais espessos (Figura 6-38).
As condições experimentais das peças mostradas na Figura 6-38 são as seguintes:
O material do tubo é aço de baixo carbono, Dfora = 90mm, t0 = 2,4mm, e o raio H é de 150mm.
O diâmetro da matriz Dd (Figura 6-37d) é de 97 mm.
O diâmetro do punção (Figura 6-37d) é Dp =72mm.
6) Devido à ausência de fricção e às duplas restrições do punção e da matriz na parede da peça, a peça tem uma maior precisão dimensional (Figura 6-37d).