Já alguma vez se perguntou como funcionam os pequenos rebites que unem estruturas maciças? Neste artigo, vamos desvendar o fascinante mundo das ligações de rebites, explorando os seus tipos, cálculos de resistência e aplicações no mundo real. No final, compreenderá o papel crucial que estes pequenos componentes desempenham nas maravilhas da engenharia. Fique atento para saber como os rebites mantêm o nosso mundo bem preso!
As uniões por rebites são um método fundamental para unir duas ou mais peças de material, particularmente metal, e são amplamente utilizadas em várias aplicações de engenharia e construção. Os rebites, que são fixadores mecânicos permanentes, são constituídos por um eixo cilíndrico liso com uma cabeça numa das extremidades. O processo de instalação consiste em inserir o rebite num orifício pré-perfurado e, em seguida, deformar a extremidade traseira para criar uma segunda cabeça, fixando assim os materiais entre si.
Historicamente, as ligações rebitadas têm sido essenciais na construção de estruturas significativas. Exemplos notáveis incluem a Torre Eiffel em Paris e a Ponte Golden Gate em São Francisco. Estas estruturas demonstram a durabilidade e a resistência das juntas rebitadas, que resistiram ao teste do tempo e continuam a funcionar de forma fiável.
A disposição dos rebites em padrões como corrente, ziguezague ou escalonado influencia o desempenho da junta.
Os rebites podem ser feitos de vários materiais, incluindo alumínio, aço, latão e cobre. A escolha do material depende de requisitos específicos como a força, a resistência à corrosão e a ductilidade.
As juntas rebitadas são preferidas em cenários onde a junta tem de suportar cargas dinâmicas e onde é necessário unir materiais diferentes. São também escolhidas pelo seu significado histórico e fiabilidade comprovada em estruturas críticas.
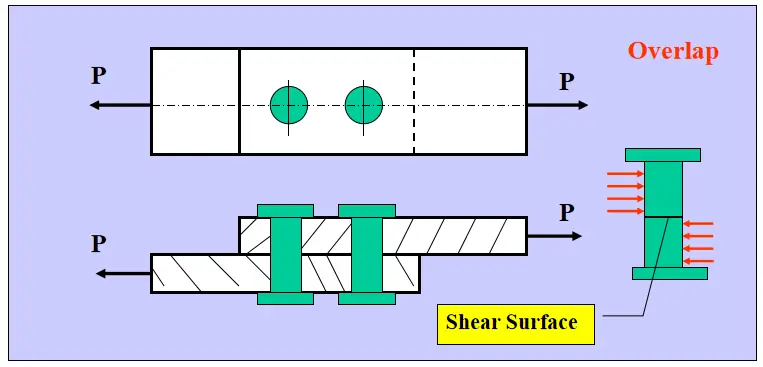
Junta de topo de tampa simples
Junta de topo de cobertura dupla
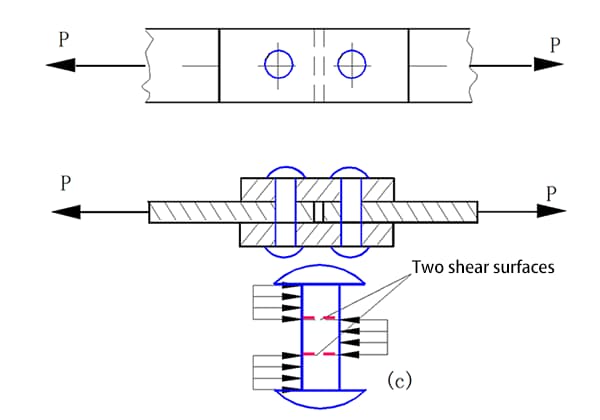
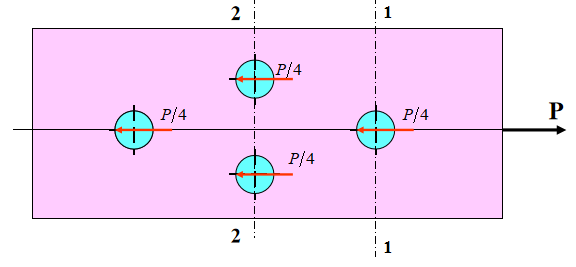
Suporte de carga lateral do grupo de rebites
Na junta rebitada (como mostrado na figura acima), para simplificar os cálculos, assuma que:
A fórmula para calcular a força que actua em cada rebite é
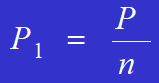
Exemplo:
Uma junta com quatro rebites é utilizada para ligar duas placas de aço. O material das chapas de aço e dos rebites é o mesmo. O diâmetro dos rebites é d=16mm, o tamanho da placa de aço é chapa de aço é b=100mm, t=10mm, P=90KN, a tensão admissível dos rebites é [τ]=120MPa, a tensão de cedência admissível é [σjy]=120MPa, e a tensão de tração admissível da chapa de aço é [σ]=160MPa. Calcular e verificar a resistência da junta rebitada.
(1) Resistência ao cisalhamento dos rebites:
A força que actua em cada rebite é P/4.
A força de corte que actua em cada rebite é dada por:
(2) Resistência ao esmagamento dos rebites:
A força que actua em cada rebite devido ao esmagamento é:
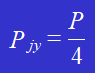
A área do rebite que está a ser esmagada é:
(3) Resistência à tração da chapa de aço
Pergunta de reflexão:
Área da superfície de corte da cavilha A.
Área da superfície de extrusão para a cavilha Ajy.
Pergunta adicional:
Fazer um furo com a forma indicada na figura num 5 mm de espessura chapa de aço. Se o limite de resistência ao cisalhamento do material da chapa de aço for 𝜏𝑏 = 300MPa, calcule a força de perfuração F necessária para o prensa de punção.
Solução: A área da superfície de cisalhamento é
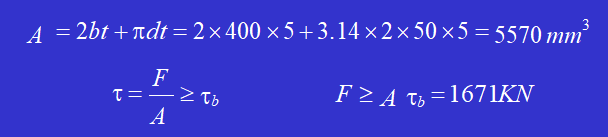
Pergunta adicional:
A força máxima de perfuração de um prensa de punção é P = 400KN, a tensão de compressão admissível [𝜎] do material de perfuração é 440MPa, e o limite de resistência ao cisalhamento da chapa de aço é 𝜏𝑏 = 360MPa. Determine o diâmetro mínimo d que o punção pode perfurar e a espessura máxima 𝜹 da placa de aço que pode ser perfurada.
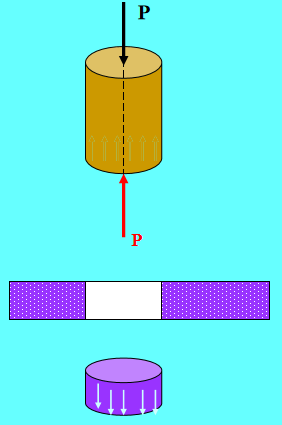
Solução: O punção sofre uma deformação axial por compressão.
De acordo com a condição de falha de cisalhamento da placa de aço:
Exemplo:
Utilizando duas calhas de aço para rebitar numa viga composta, a situação de ligação é mostrada nas figuras a e b.
A área da secção transversal de cada carril de aço A é de 8000mm, e o momento de inércia da área da secção transversal de cada carril de aço em relação ao seu próprio centroide é I = 1600 × 10mm. O espaçamento entre rebites s é de 150mm, o diâmetro é d = 20mm, e a tensão de cisalhamento admissível [τ] é de 95MPa. Se a força de corte interna Q da viga for 50kN, verificar a resistência ao corte dos rebites. O atrito entre as calhas de aço superior e inferior não é considerado.
Solução: Quando os dois carris de aço superior e inferior se dobram como um todo, a área da secção transversal do carril de aço superior está sob tensão de compressão e a área da secção transversal do carril de aço inferior está sob tensão de tração.
Devido aos diferentes momentos de flexão em secções transversais adjacentes, a tensão normal nos pontos correspondentes é diferente e, por conseguinte, há uma tendência para o deslocamento longitudinal ao longo da superfície de contacto entre os carris de aço superiores e inferiores, fazendo com que os rebites suportem forças de corte.
A força de corte suportada por cada fila de rebites é igual à diferença de força de compressão (tração) em duas secções transversais de um carril de aço a uma distância longitudinal de S.
Assumindo que os carris de aço transmitem tensão de corte em toda a superfície de contacto, a largura da superfície de contacto é b.
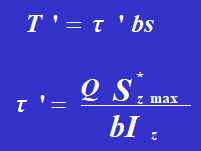
Szmax representa o momento estático da secção transversal de um carril de aço em relação ao eixo neutro.
Iz é o momento de inércia de toda a área da secção transversal em relação ao eixo neutro.
A tensão de cisalhamento do rebite é:
A tensão de cisalhamento do rebite satisfaz os critérios de resistência.
Conjunto de rebites sujeito a cargas de torção (ver figura).
Seja o centróide da secção transversal do conjunto de rebites o ponto 0.
Assumindo que qualquer linha reta na chapa de aço (tal como OA ou OB) permanece reta após a rotação, a tensão de corte média de cada rebite é proporcional à distância do centro da secção transversal do rebite ao ponto O.
Se o diâmetro de cada rebite for o mesmo, a força em cada rebite é proporcional à distância do centro da secção transversal do rebite ao centro do centro seccional O da montagem do rebite, com a direção perpendicular à linha que liga o ponto ao centro O.
Pi representa a força que actua em cada rebite, e ai representa a distância do centro da secção transversal de um determinado rebite ao centróide da secção transversal do conjunto de rebites, denotado como O.
O conjunto de rebites sujeito a cargas laterais excêntricas (ver Figura a).
Simplificando a carga excêntrica P que actua no conjunto de rebites para o ponto central O, obtém-se uma força P que passa pelo ponto O e um momento m = Pe que gira em torno do ponto O.
Se o diâmetro de cada rebite no mesmo conjunto de rebites for o mesmo, a força P1′ causada pela força lateral P e a força P1" causada pelo momento m podem ser calculadas. A força que actua sobre cada rebite é a soma vetorial de P1′ e P1". Depois de determinar a força P1 em cada rebite, a resistência ao cisalhamento e à compressão do rebite com a força máxima pode ser verificada separadamente.
Exemplo:
Um suporte ligado por um único rebite está sujeito a uma força concentrada P, como se mostra na Figura a. Sabe-se que a força externa P é de 12 kN. O diâmetro do rebite é de 20 mm, e cada rebite está sujeito a um único cisalhamento. Calcule a tensão de cisalhamento máxima na secção transversal do rebite sob a força máxima.
Solução:
O conjunto de rebites é simétrico em relação ao eixo x, e o centro de rotação está no ponto O, que é o ponto de intersecção da linha que liga o rebite 2 e o rebite 5 com o eixo x.
1. Simplificando a força P para o ponto O, temos:
P = 12 kN.
m=12 0,12=1,44KN.m
2. Sob a ação da força P que passa pelo centro de rotação, e considerando que cada rebite tem o mesmo diâmetro e material, a força em cada rebite é igual.
3. Sob a ação do momento m, a força que cada rebite suporta é proporcional à distância do rebite ao centro de rotação.
De acordo com a equação de equilíbrio:
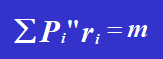
Resolvendo a equação, obtemos:
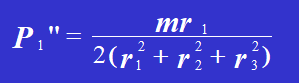
Por conseguinte,
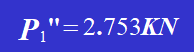
4. Desenhe o diagrama de forças de cada rebite e combine os vectores Pi' e Pi" para obter a força de corte total que actua em cada rebite, incluindo a sua magnitude e direção. Pode concluir-se que o rebite 1 e o rebite 6 suportam a força máxima, sendo o valor da força máxima:
A tensão de cisalhamento na secção transversal do rebite é:
Seguem-se as respostas a algumas perguntas frequentes:
Na construção, são utilizados vários tipos de rebites devido às suas propriedades e aplicações únicas. Os rebites sólidos, também conhecidos como rebites redondos, são o tipo mais comum e mais antigo, consistindo num eixo sólido e numa cabeça. São instalados deformando a cauda com um martelo ou uma ferramenta de cravar e são amplamente utilizados devido à sua elevada resistência e fiabilidade. Os rebites de aço estrutural são semelhantes aos rebites sólidos, mas são concebidos para aplicações de alta tensão na construção comercial, como pontes e edifícios altos.
Os rebites cegos, ou rebites pop, são rebites tubulares com um mandril no centro, instalados com um rebitador. São ideais para aplicações em que o acesso à parte traseira da junta é limitado. Os rebites de acionamento, semelhantes aos rebites cegos, não necessitam de uma ferramenta especial para a instalação e são colocados no lugar com um martelo, sendo adequados para aplicações em que os orifícios não penetram em todo o painel ou bloco.
Os rebites de embutir, ou rebites escareados, têm cabeças e orifícios escareados, o que lhes permite ficarem nivelados com a superfície, reduzindo a resistência aerodinâmica e proporcionando um acabamento de superfície suave. Os rebites divididos, ou rebites bifurcados, apresentam extremidades afiadas que se dividem em direcções opostas quando inseridas num material, sendo ideais para unir materiais macios como a madeira, o plástico e o couro. Os rebites tubulares são ocos, com uma cabeça numa extremidade e uma cauda na outra, exigindo menos força para serem instalados e utilizados em aplicações em que os materiais a fixar são macios.
Os rebites são feitos de vários materiais, incluindo aço inoxidável, aço, alumínio, latão e cobre, cada um escolhido com base nos requisitos específicos do projeto. Estes materiais oferecem diferentes forças, resistência à corrosão e caraterísticas de peso, tornando os rebites versáteis para uma série de aplicações de construção.
Ao comparar ligações rebitadas com ligações soldadas, surgem várias diferenças e considerações importantes. As juntas soldadas oferecem geralmente maior resistência e capacidade de carga em comparação com as juntas rebitadas. Uma boa junta soldada pode atingir 100% da resistência do material de base, enquanto que as juntas rebitadas têm uma resistência inferior devido à redução da área da secção transversal causada pelos furos feitos para os rebites.
Em termos de conceção e instalação, a soldadura é muitas vezes mais simples e rápida, uma vez que não requer furos pré-perfurados ou peças adicionais como rebites. A rebitagem, no entanto, envolve a perfuração, a fixação e o achatamento dos rebites, o que a torna mais demorada e trabalhosa.
O desempenho sob vibração e fadiga difere entre os dois métodos. As juntas rebitadas resistem melhor às cargas cíclicas e às vibrações porque a deformação e a expansão dos rebites podem reforçar a ligação ao longo do tempo. As juntas soldadas, embora fortes, podem ser mais susceptíveis à degradação sob ciclos de carga repetidos.
No que diz respeito aos materiais e à compatibilidade, a rebitagem é mais versátil para unir materiais diferentes, uma vez que não requer a consideração dos pontos de fusão. A soldadura, no entanto, requer materiais com pontos de fusão e propriedades térmicas compatíveis.
Esteticamente, as juntas soldadas podem proporcionar um acabamento de superfície mais suave após o pós-processamento, que é frequentemente mais agradável em comparação com as cabeças de rebite visíveis das juntas rebitadas.
No que respeita à manutenção e desmontagem, as juntas rebitadas são mais fáceis de desmontar e reparar, uma vez que os rebites podem ser perfurados e substituídos. As juntas soldadas são mais permanentes e requerem um corte e uma nova soldadura para a desmontagem, o que é mais moroso e dispendioso.
Em termos de peso e integridade estrutural, as estruturas soldadas são normalmente mais leves porque não requerem materiais adicionais como rebites e cintas. As estruturas rebitadas podem ser mais pesadas devido a estes componentes adicionais.
O custo e a eficiência também desempenham um papel importante na escolha entre os dois métodos. A rebitagem tende a ser mais cara em geral, apesar do baixo custo dos rebites individuais, devido à acumulação de custos de material, operacionais e de mão de obra. A soldadura, especialmente com processos automatizados, pode ser mais económica e rápida.
Em resumo, a escolha entre rebitagem e soldadura depende dos requisitos específicos da aplicação, incluindo necessidades de resistência, compatibilidade de materiais, considerações estéticas e requisitos de manutenção. A soldadura oferece uma maior resistência, uma conceção mais simples e uma produção mais rápida, mas pode introduzir distorção térmica e é menos flexível para a desmontagem. A rebitagem proporciona uma melhor resistência à vibração, uma desmontagem mais fácil e a capacidade de unir materiais diferentes, mas é geralmente mais fraca e mais trabalhosa.
As juntas rebitadas são amplamente utilizadas na engenharia moderna devido à sua durabilidade, fiabilidade e vantagens específicas em relação a outros métodos de união. Na indústria aeroespacial, as juntas rebitadas são cruciais para a ligação de componentes como os painéis da fuselagem e as asas, onde as suas caraterísticas de leveza e elevada resistência são essenciais para manter a integridade estrutural, minimizando o peso. Na construção naval, as juntas rebitadas são indispensáveis para a montagem de cascos e outras peças-chave de navios, oferecendo resistência à pressão da água e à corrosão, o que é fundamental para garantir a integridade estanque e a segurança em águas agitadas.
Nos sectores da construção e das infra-estruturas, as juntas rebitadas são utilizadas em estruturas como pontes, torres e edifícios. Estas juntas são valorizadas pela sua capacidade de distribuir uniformemente as cargas e proporcionar estabilidade a grandes estruturas, tornando-as ideais para aplicações que requerem um suporte robusto, como em vigas de pontes e treliças. Para vasos de pressão e caldeiras, as juntas rebitadas são preferidas quando os processos térmicos, como a soldadura, podem ser impraticáveis ou quando as juntas têm de suportar flutuações de temperatura e vibrações.
As indústrias automóvel e dos transportes públicos também beneficiam das juntas rebitadas, nomeadamente no fabrico de carroçarias de autocarros e tróleis. Estas juntas asseguram ligações fortes e fiáveis, capazes de suportar as tensões e vibrações associadas a estes veículos. Além disso, as juntas rebitadas são encontradas em produtos de consumo, como utensílios de cozinha e canivetes, onde a sua força, leveza e resistência à corrosão são vantajosas.
Em geral, as juntas rebitadas são preferidas em ambientes sujeitos a vibrações ou cargas dinâmicas devido à sua resistência ao afrouxamento ao longo do tempo. São também adequadas para as indústrias sujeitas a flutuações de temperatura, uma vez que não necessitam de calor para a instalação e são resistentes à expansão térmica. Além disso, as juntas rebitadas são mais fáceis de inspecionar e desmontar do que as juntas soldadas, com menos danos para as peças envolvidas. Estas caraterísticas tornam as juntas rebitadas um método preferido em várias indústrias críticas e de alto desempenho.
As ligações rebitadas oferecem várias vantagens e desvantagens, tornando-as adequadas para aplicações específicas e apresentando desafios noutras.
As vantagens da utilização de ligações rebitadas incluem a relação custo-eficácia, uma vez que os rebites são baratos e não requerem eletricidade ou materiais especiais, poupando nos custos de material e energia. A rebitagem também aumenta o rendimento da produção, uma vez que geralmente requer menos equipamento e preparação em comparação com a soldadura, reduzindo assim o tempo e os recursos necessários. O processo gera um mínimo de resíduos, aumentando a eficiência. As ligações rebitadas proporcionam flexibilidade no design e são mais fáceis de inspecionar e manter; os rebites gastos podem ser rapidamente substituídos com o mínimo de equipamento. São versáteis, capazes de unir metais ferrosos e não ferrosos, bem como materiais não metálicos como madeira, plástico e folhas de amianto. A rebitagem é amiga do ambiente e do utilizador, não produzindo fumos ou gases, o que a torna mais segura para os trabalhadores. Além disso, as juntas rebitadas oferecem uma elevada resistência ao cisalhamento e uma boa resistência à fadiga, adequadas para aplicações sujeitas a vibrações e forças de impacto.
No entanto, as ligações rebitadas também têm desvantagens. Requerem um maior esforço de mão de obra, envolvendo várias etapas, como a perfuração de furos e a instalação dos rebites, o que pode aumentar os custos de mão de obra. Os rebites aumentam o peso da estrutura, o que pode ser significativo em estruturas de grandes dimensões e pode afetar a eficiência estrutural. Os furos necessários para os rebites podem enfraquecer as chapas metálicas, levando a uma concentração de tensões à volta dos furos, exigindo potencialmente uma espessura adicional ou a sobreposição de chapas para manter a integridade estrutural. Esteticamente, as ligações rebitadas são mais visíveis e podem sobressair da estrutura, reduzindo a atração visual em comparação com as juntas soldadas. A rebitagem pode ser ruidosa durante a instalação e pode ser propensa à corrosão se não for corretamente selada, aumentando os custos de manutenção ao longo do tempo. As juntas rebitadas podem não proporcionar uma vedação estanque ou à prova de fugas, a menos que sejam utilizados rebites quentes ou vedantes, o que pode ser uma desvantagem em determinadas aplicações. Finalmente, embora os rebites possam ser substituídos, o processo pode ser incómodo e ruidoso, e a substituição de rebites durante a manutenção pode ser mais difícil em comparação com outros métodos de fixação, como os parafusos.
Em resumo, as ligações rebitadas são rentáveis e flexíveis, mas implicam maiores requisitos de mão de obra, peso estrutural acrescido, problemas de concentração de tensões e limitações estéticas. A escolha entre a rebitagem e outros métodos de união depende dos requisitos específicos do projeto.
Manter e reparar eficazmente as ligações rebitadas envolve vários passos cruciais para garantir a integridade e a longevidade da estrutura. A inspeção regular é fundamental; verifique se as juntas rebitadas apresentam sinais de desgaste, corrosão e fadiga. Limpe as ligações periodicamente para remover quaisquer detritos, sujidade ou substâncias corrosivas que possam comprometer a junta. Para limpar as pistolas de rebites pneumáticas utilizadas na manutenção, assegure uma limpeza, lubrificação e inspeção minuciosas das mangueiras de ar e dos acessórios para evitar avarias.
Quando se trata de reparações, comece por identificar quaisquer falhas, tais como tamanhos incorrectos de rebites ou preparação inadequada dos furos. Se os rebites tiverem de ser substituídos, remova-os cuidadosamente, perfurando a cabeça e utilizando um punção para retirar a haste sem danificar o material circundante. Substitua sempre os rebites com o tamanho e tipo corretos, assegurando técnicas de instalação adequadas para evitar problemas como cabeças inclinadas ou fissuras.
Para reparações mais extensas, podem ser utilizadas técnicas especializadas, tais como a soldadura por fricção e por anel, particularmente em rebites mais antigos ou muito danificados. É também crucial abordar qualquer potencial corrosão selando corretamente as juntas, especialmente quando estão envolvidos metais diferentes, para evitar a corrosão galvânica.
Assegurar que as juntas rebitadas não são sujeitas a fadiga e vibração excessivas, que podem conduzir a falhas. Evitar a compressão excessiva durante a instalação para evitar vazios ou o endurecimento do metal. Após as reparações, realize testes e inspecções minuciosos para confirmar a integridade estrutural e a estanquidade das juntas. Resolva imediatamente quaisquer fugas com calafetagem adicional ou ajustes de rebites.
Se seguir estas diretrizes de manutenção e reparação, pode manter a resistência, fiabilidade e segurança das suas ligações rebitadas ao longo do tempo.
Como fundador da MachineMFG, dediquei mais de uma década da minha carreira à indústria metalúrgica. A minha vasta experiência permitiu-me tornar-me um especialista nos domínios do fabrico de chapas metálicas, maquinagem, engenharia mecânica e máquinas-ferramentas para metais. Estou constantemente a pensar, a ler e a escrever sobre estes assuntos, esforçando-me constantemente por me manter na vanguarda da minha área. Deixe que os meus conhecimentos e experiência sejam uma mais-valia para a sua empresa.
PT 
EN 
AR 
DE 
ES 
FR 
ID 
IT 
JA 
NL 
PT_BR 
RU 
KO 
TR