Alguma vez teve dificuldade em desdobrar com exatidão peças de chapa metálica? Este artigo explora a arte e a ciência por trás dos cálculos de desdobramento de chapas metálicas. Descubra os principais conceitos, fórmulas e técnicas utilizados por engenheiros experientes para desdobrar com precisão geometrias complexas. Saiba como aplicar estes princípios aos seus próprios projectos e simplificar o seu processo de fabrico.
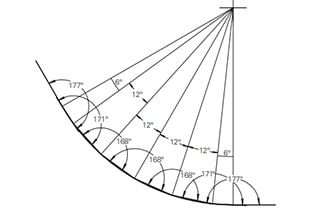
O primeiro passo no processo de fabrico de chapas metálicas é o desdobramento das geometrias e do corpo coerente. A precisão e a correção do desdobramento da amostra têm um impacto direto na qualidade da peça final.
No passado, devido às limitações das ferramentas de cálculo, as pessoas utilizavam o método de projeção para ampliar a amostra num plano com uma relação 1:1 e medir o comprimento real da linha de plano necessária.
No entanto, este método é complicado e ineficaz e não pode satisfazer as actuais exigências da produção.
Com os avanços nos instrumentos de cálculo, como as calculadoras electrónicas e a utilização generalizada de computadores, chapa metálica pode agora ser efectuado através de métodos de cálculo.
Para normalizar o método de cálculo do coeficiente de desdobramento de chapas metálicas pelos técnicos, minimizar os desvios dimensionais dos produtos após a dobragem e facilitar a auto-inspeção pelo pessoal da oficina e a reinspecção pelos inspectores de qualidade, existe uma norma e uma base unificadas para o coeficiente de desdobramento.
Como resultado, a norma de cálculo para o coeficiente de desdobramento de chapa metálica tornou-se cada vez mais normalizada.
Método de desdobramento da camada neutra
No processo de flexão, a camada exterior sofre tensão de tração, enquanto a camada interior sofre tensão de compressão. A camada de transição entre a tensão de tração e a tensão de compressão é designada por camada neutra. O comprimento da camada neutra durante a dobragem permanece o mesmo que antes da dobragem, o que a torna a referência para determinar o comprimento desdobrado da peça dobrada.
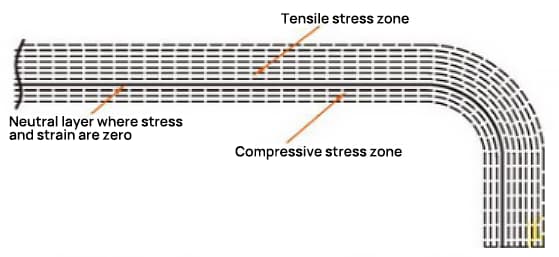
A localização da camada neutra depende do grau de deformação.
A posição da camada neutra não está apenas relacionada com o raio de curvatura, a espessura da chapa, o coeficiente de deslocamento para o interior, etc., mas também com factores como o método de processamento, a forma e o tamanho da chapa metálica.
Por conseguinte, a posição da camada neutra só pode ser determinada de forma aproximada e, em aplicações práticas, são geralmente utilizados valores aproximados para o cálculo.
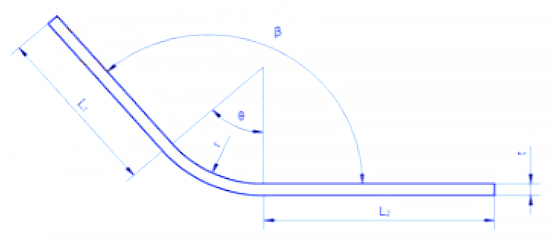
A fórmula de cálculo para a dimensão do comprimento L da camada neutra é a seguinte
Entre eles,
Utilizando software 3D para realizar simulações e cálculos de várias espessuras, ângulos e raios, juntamente com práticas de fabrico no local, compilámos um conjunto de valores de fator K. Consulte a Tabela 1 para obter os valores específicos.
Tabela 1: Valores K do coeficiente da camada neutra
| r/t | ≤05 | 0.6 | 0.8 | 1 | 1.2 | 1.3 | 1.5 | 2 | 2.5 | 3.0 | 4.0 | 5.0 | 6.0 | ≥8 |
| k | 026 | 0.28 | 0.30 | 0.32 | 0.33 | 0.34 | 0.36 | 0.38 | 0.39 | 0.4 | 0.42 | 0.44 | 0.46 | 0.5 |
Cálculo de desdobramento rápido para curvas de 90°
O diagrama de desdobramento para uma curva de 90° é apresentado na Figura 9. Nos últimos anos, utilizámos software 3D como o CATIA e o SOLIDWORKS para modelação de chapas metálicas para calcular as dimensões de desdobramento.
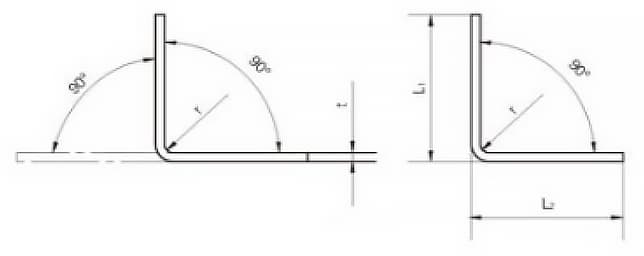
Através de verificações repetidas, observou-se que, quando o ângulo de flexão a frio dos produtos planos de aço é de 90°, a fórmula para calcular o comprimento desdobrado L é
L = L1 + L2 - A
Onde,
Tabela 2 Tabela de parâmetros de flexão a 90
| Espessura t/mm | Raio de assentamento r/mm | |||||||||||
| 1 | 1.2 | 16 | 2 | 25 | 3 | 4 | 5 | 6 | 8 | 10 | 12 | |
| Valor de compensação A mm | ||||||||||||
| 1 | -1.92 | -1.97 | -2.10 | -2.23 | -2.41 | -2.59 | -2.97 | -3.36 | -3.79 | -4.65 | -5.51 | -6.37 |
| 1.5 | -2.90 | -3.02 | -3.18 | -3.34 | -3.70 | -4.07 | -4.45 | -5.26 | -6.11 | -6.97 | ||
| 2 | -3.84 | -3.98 | -4.13 | -4.46 | -4.81 | -5.18 | -5.94 | -6.72 | -7.58 | |||
| 2.5 | -4.80 | -4.93 | -5.24 | -5.57 | -5.93 | -6.66 | -7.42 | -8.21 | ||||
| 3 | -5.76 | 6.04 | -6.35 | -6.69 | -7.40 | -8.14 | -8.91 | |||||
| 4 | -7.7 | -7.95 | -8.26 | -8.92 | -9.62 | -10.36 | ||||||
| 5 | -9.6 | -9.87 | -10.48 | -11.15 | -11.85 | |||||||
| 6 | -11.5 | -12.08 | -12.71 | -13.38 | ||||||||
| 8 | -15.4 | -15.9 | -16.51 | |||||||||
| 10 | -19.2 | -19.73 | ||||||||||
| 12 | 23.01 | |||||||||||
Quando o raio de curvatura é grande e o ângulo de flexão é pequeno, o grau de deformação é baixo e a camada neutra está próxima do centro da espessura da chapa.
No entanto, quando o raio de curvatura (R) se torna mais pequeno e o ângulo de flexão (θ) aumenta, o grau de deformação também aumenta e a camada neutra desloca-se para o lado interior do centro de flexão. A distância entre a camada neutra e o lado interior da chapa é designada por λ e a espessura do material é designada por T.
A fórmula básica para calcular o comprimento de desdobramento:
Comprimento de desdobramento = dimensão interior do material + dimensão interior do material + montante da compensação.
Também pode utilizar a seguinte calculadora para calcular o comprimento de desdobramento da chapa metálica:

De seguida, descrevem-se, um a um, os algoritmos de desdobramento de várias características de curvatura.
R = 0mm, θ = 90° (Nota: Quando R ≤ 1,0mm, é tratado como R = 0mm).
L = A + B + K
Na produção real, a matriz superior de dobragem pode usar um ângulo R, ou pode haver um ângulo R inferior a 1 mm, ou a escolha do matriz inferiorpode ser grande, entre outras razões, resultando num coeficiente de flexão pequeno. Consequentemente, o coeficiente de flexão de cada espessura de placa de material é apresentado no Quadro 1 com base em valores empíricos actuais.
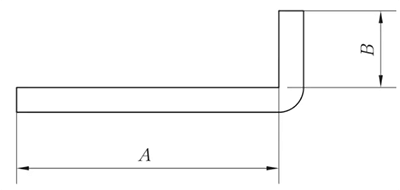
Fig. 1 Diagrama esquemático da flexão geral I
R ≠ 0mm e θ = 90°
L = A + B + K (K é o comprimento do arco da camada neutra)
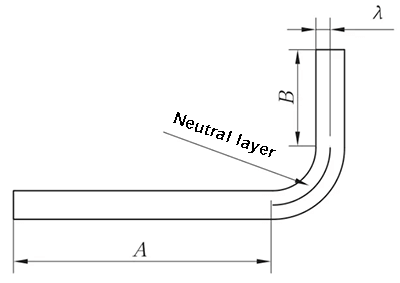
Fig. 2 Diagrama esquemático da flexão geral II
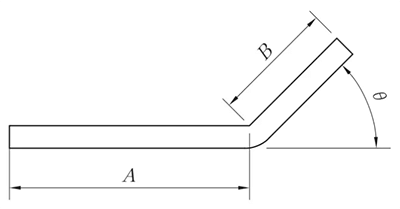
R = 0mm, θ ≠ 90°
L = A + B + K'
Nota: K é o montante de compensação a 90°.
R ≠ 0mm, θ ≠ 90°
L = A + B + K
(K é o comprimento do arco da camada neutra)
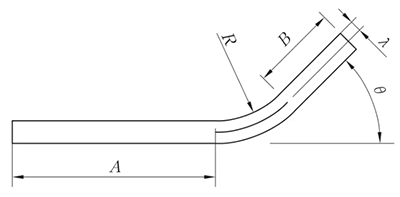
Fig. 4 Flexão geral IV diagrama de curvatura
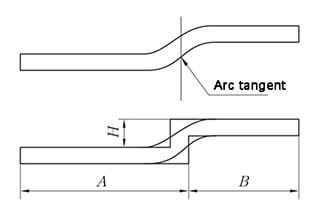
O método de desdobramento é equivalente ao método de dobragem em Z com aresta reta paralela, e a medição da altura é demonstrada na Figura 6.
O ângulo θ é considerado um desdobramento de 90°.
Para 0 < T ≤ 1,6mm, λ é igual a 0,5T.
Quando T é superior a 1,6mm, λ é igual a 0,4T.
Z-Fold, também designado por Dobragem de desvioA curvatura por deslocamento de borda reta e a curvatura por deslocamento de borda biselada são diferenciadas com base no ângulo de formação e o método de processamento é determinado pela altura de deslocamento.
Quando a altura de desvio, h, é inferior a 3,5 vezes a espessura do material, matrizes offset ou matrizes amovíveis são utilizadas para a enformação.
Se a altura de desvio exceder 3,5 vezes a espessura do material, é utilizada a formação normal positiva e negativa.
Quando o comprimento da aresta chanfrada é inferior a 3,5 vezes a espessura do material, são utilizadas matrizes de offset ou matrizes modificáveis para a conformação.
Se o comprimento da aresta biselada exceder 3,5 vezes a espessura do material, é aplicada a dobragem normal de um positivo e um negativo.
(1) Quando H < 3,5T, só então pode ser processado por dobragem por deslocamento.
L = A + B + H
(se H ≤ T, então compensar 0,2 mm)
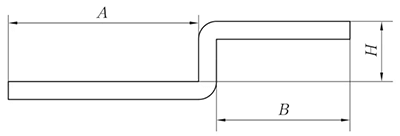
Fig. 5 Diagrama esquemático do desvio da régua
(2) Desvio não paralelo da vara
O método de expansão é o mesmo que o método de dobragem em Z com régua paralela, e o valor da altura é apresentado na Figura 6.
O ângulo θ pode ser considerado como um desdobramento de 90°.
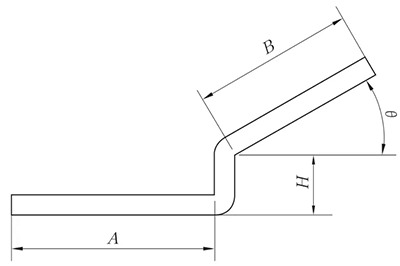
Fig. 6 Diagrama esquemático do desvio não paralelo da vara
(3) Desvio de reta - o segmento de transição é tangente a dois arcos
Quando o Straight-Edge Offset é desdobrado no ponto tangente de dois arcos de círculo, é criada uma linha vertical no ponto tangente dos dois arcos de círculo na superfície exterior do substrato. O material é então deslocado por uma espessura de material para dentro, como ilustrado na Figura 7, para processamento e desdobrado utilizando o método Z-Fold 1 (Straight-Edge Offset).
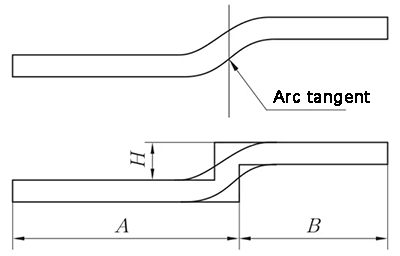
Fig. 7 Diagrama de desvio de aresta reta - o segmento de transição é tangente a dois arcos de círculo
Quando H < 2T, o algoritmo de desdobramento é o seguinte, de acordo com o processamento de deslocamento.
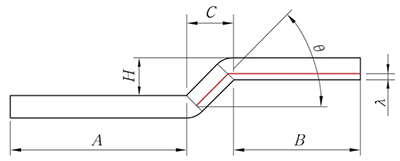
Fig. 8 Diagrama da deslocação da aresta biselada
L = A + B - K
(1) Ao aplanar, considerar a possibilidade de pressionar a linha antes de a dobrar, com base nas condições reais.
A localização da linha de prensagem é no centro da área de deformação por flexão.
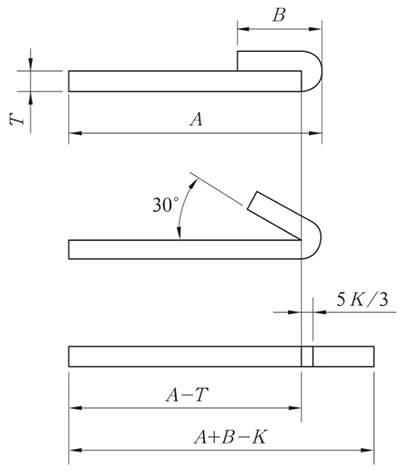
Fig. 9 Diagrama esquemático da dobragem inversa e do achatamento
Os processos de dobragem inversa e de aplanamento são normalmente efectuados em duas etapas: primeiro, o material é dobrado a 30° utilizando a matriz de inserção, seguido de aplanamento.
Por conseguinte, ao criar o linha de dobragem no desenho ampliado, é essencial ilustrar a linha de curvatura com base na curvatura de 150°, como demonstrado na Figura 9.
Tabela 1 Coeficiente de flexão de placas com diferentes espessuras sob diferentes ângulos de flexão
| Ângulo | Espessura/mm | ||||
|---|---|---|---|---|---|
| 1 | 1.2 | 1.5 | 1.8 | 2.5 | |
| 45° | 5.3 | 6.3 | 7.8 | 9.5 | 13 |
| 50° | 4.5 | 5.4 | 6.8 | 8.1 | 11.25 |
| 55° | 4 | 4.7 | 5.8 | 7.05 | 9.75 |
| 60° | 3.4 | 4.1 | 5.1 | 6.15 | 8.5 |
| 65° | 3 | 3.6 | 4.5 | 5.4 | 7.5 |
| 70° | 2.65 | 3.2 | 4 | 4.75 | 6.6 |
| 75° | 2.35 | 2.8 | 3.5 | 4.25 | 5.9 |
| 80° | 2.1 | 2.5 | 3.1 | 3.75 | 5.25 |
| 85° | 1.9 | 2.25 | 2.8 | 3.35 | 4.65 |
| 90° | 1.7 | 2 | 2.5 | 3 | 4.15 |
| 95° | 1.5 | 1.8 | 2.2 | 2.7 | 3.75 |
| 100° | 1.35 | 1.6 | 2 | 2.4 | 3.35 |
| 105° | 1.2 | 1.4 | 1.75 | 2.15 | 3 |
| 110° | 1.1 | 1.3 | 1.6 | 2 | 2.65 |
| 115° | 1 | 1.25 | 1.4 | 1.7 | 2.35 |
| 120° | 0.85 | 1 | 1.25 | 1.5 | 2.1 |
| 125° | 0.75 | 0.9 | 1.1 | 1.35 | 1.85 |
| 130° | 0.65 | 0.8 | 1 | 1.18 | 1.65 |
| 135° | 0.55 | 0.7 | 0.85 | 1.05 | 1.45 |
| 140° | 0.5 | 0.6 | 0.75 | 0.9 | 1.25 |
| 145° | 0.43 | 0.5 | 0.65 | 0.77 | 1.05 |
| 150° | 0.35 | 0.43 | 0.55 | 0.65 | 0.9 |
| 155° | 0.3 | 0.35 | 0.45 | 0.53 | 0.75 |
| 160° | 0.23 | 0.27 | 0.35 | 0.4 | 0.6 |
| 165° | 0.17 | 0.2 | 0.25 | 0.3 | 0.45 |
O método de processamento N-fold envolve tanto a remodelação como o achatamento, e o algoritmo de desdobramento é:
L = A + B + K
(K é o comprimento do arco da camada neutra).
λ = 0,5T
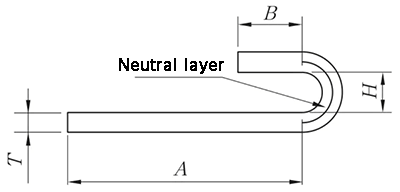
Fig.10 Diagrama N-fold
(1) A expansão do arco é diretamente K, e o comprimento do arco da camada neutra é tomado. λ= 0.5T
(2) Expansão com a borda reta de um lado.
L = A + K
(k é o comprimento do arco da camada neutra)
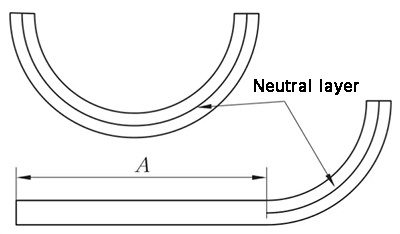
Fig. 11 Diagrama esquemático da flexão em arco
Na produção real, o controlo preciso do comprimento desdobrado da chapa metálica através de software 3D pode ser conseguido principalmente através dos seguintes passos e métodos:
Escolha o software de desenho 3D correto: Em primeiro lugar, é necessário escolher um software CAD 3D adequado para o desenho de chapas metálicas. SolidEdge, Creo, FreeCAD, UG, etc. são todos softwares que podem ser utilizados para o desenho de chapas metálicas. Estes softwares fornecem módulos de chapa metálica ou funções relacionadas que podem ajudar os projectistas na conceção e nos cálculos de desdobramento de peças de chapa metálica.
Utilizar o módulo de chapa metálica ou as ferramentas do software: A maior parte do software CAD 3D fornece ferramentas e funções relacionadas com o desenho de chapas metálicas. Por exemplo, o Creo oferece uma variedade de métodos para controlar as dimensões desdobradas da chapa metálica, incluindo os métodos de modelação e desdobramento de peças de chapa metálica de grande arco, o método de dedução de dobras, etc. O FreeCAD, enquanto software de modelação 3D de código aberto, também dispõe de um módulo de chapa metálica.
Aplicaçãométodos de cálculo de desdobramento: Para garantir a exatidão do comprimento após o desdobramento da chapa metálica, podem ser utilizados diferentes métodos de cálculo de desdobramento. Os métodos mais comuns incluem o método de compensação de dobragem, o método de dedução de dobragem e o método de cálculo do fator K. Estes métodos podem ajudar os projectistas a calcular o comprimento real do material no estado desdobrado, garantindo assim o tamanho esperado das peças após a dobragem e conformação finais.
Preste atenção ao manuseamento de arestas e cantos e ao ajuste de pormenores: No processo de conceção de chapas metálicas, os pormenores do manuseamento de arestas e cantos são muito importantes. Alguns softwares, como o SW, fornecem uma variedade de soluções de manuseamento de arestas e cantos e métodos de dobragem, o que ajuda a melhorar a precisão do desdobramento.
Para curvas que não sejam de 90 graus, os ângulos de curvatura comuns incluem, mas não se limitam a, 45 graus e 135 graus. O método de cálculo do fator K baseia-se na relação entre a espessura do material e o raio de curvatura.
Especificamente, o fator K = δ / T, em que δ representa a espessura do material e T representa o raio de curvatura. Este método é aplicável para calcular o coeficiente de curvatura de qualquer ângulo que não seja de 90 graus.
Em aplicações práticas, devido às possíveis diferenças e grandes erros nos valores de dedução de curvas em diferentes ângulos, o fator K é geralmente utilizado como coeficiente de curvatura.
Além disso, para orientar com precisão o valor do fator K de diferentes espessuras de chapa, são necessários ajustes. Algumas referências sugerem que o valor do fator K para qualquer raio de curvatura pode ser calculado através de técnicas de interpolação específicas, que se revelaram eficazes para aplicações industriais de chapas metálicas.
A fórmula de cálculo para o comprimento expandido da chapa de prensa-travão biselada é [L = A + B + C + 0,2], onde (A), (B) e (C) representam as dimensões internas, e 0,2 serve como valor de compensação.
Com base nos princípios e práticas gerais dos cálculos de expansão de chapas metálicas, este valor de compensação tem em conta as discrepâncias entre os comprimentos reais e os calculados teoricamente, devido a factores como a dobragem do material e os erros de precisão do molde durante as operações reais.
No processamento de chapas metálicas, este valor de compensação ajuda a garantir a precisão dimensional e a qualidade do produto final.
As peças de chapa metálica são amplamente utilizadas na indústria eletromecânica, na indústria ligeira e na indústria automóvel.
A forma desdobrada das peças de chapa metálica é o principal fator determinante do tamanho da peça em bruto, o que, por sua vez, afecta o tamanho e a forma da peça em bruto.
No entanto, os métodos tradicionais de desdobramento de peças de chapa metálica tornaram-se cada vez mais inadequados para satisfazer as necessidades dos projectos modernos devido aos seus longos ciclos, baixa eficiência e má qualidade.
Para colmatar estas lacunas, a utilização de sistemas CAD avançados tem-se tornado cada vez mais frequente nos últimos anos.
Estes sistemas especializados de conceção de peças em chapa metálica possuem uma funcionalidade robusta e podem reduzir significativamente o tempo e o esforço necessários para a conceção preliminar e a implementação de peças em chapa metálica.