Já alguma vez se interrogou sobre como calcular com exatidão o peso de uma malha de arame? Nesta publicação do blogue, vamos explorar vários métodos e factores a considerar ao determinar o peso da malha de arame. O nosso especialista em engenharia mecânica residente guiá-lo-á ao longo do processo, fornecendo informações e exemplos práticos. No final deste artigo, terá uma compreensão clara de como estimar o peso da malha de arame para as suas necessidades específicas.
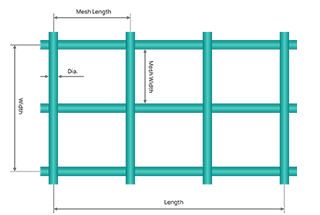
O cálculo do peso da malha de arame é crucial em várias aplicações, desde a construção até ao fabrico industrial. Saber como calcular com precisão o peso da malha de arame garante que os projectos são realizados de forma eficiente, segura e dentro do orçamento. O peso da rede metálica pode ser influenciado por vários factores, incluindo o tipo de material, o diâmetro do fio, o número de malhas e as dimensões gerais.

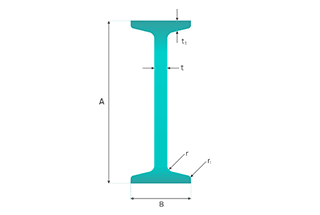
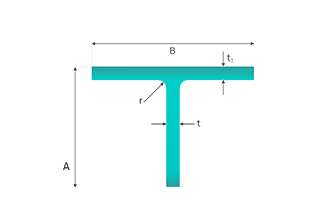
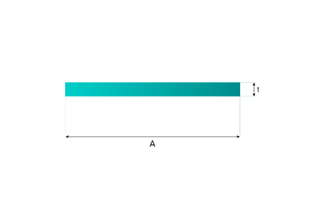
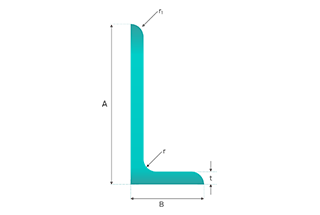
Diâmetro do fio: A espessura do fio utilizado na malha é um fator primordial. É medida em milímetros (mm) ou polegadas. Os fios mais grossos dão origem a uma malha mais pesada. Por exemplo, um diâmetro de fio de 2 mm produzirá uma malha mais pesada do que um diâmetro de fio de 1 mm, assumindo que todos os outros factores são constantes. Isto deve-se ao facto de o volume do fio aumentar com o quadrado do diâmetro, o que tem um impacto significativo no peso.
Número da malha: Refere-se ao número de aberturas por polegada linear da malha. Um número de malhas mais elevado significa mais fios e, consequentemente, mais peso por unidade de superfície. Por exemplo, uma malha com 10 aberturas por polegada (malha 10) será mais leve do que uma malha com 20 aberturas por polegada (malha 20) se o diâmetro do fio permanecer o mesmo. Este facto deve-se ao aumento da densidade dos fios no número de malhas mais elevado.
Abertura/abertura da malha: O tamanho das aberturas entre os fios, medido de centro a centro para a malha e de interior a interior para as aberturas, também afecta o peso. As aberturas mais pequenas dão origem a uma malha mais densa e mais pesada. Por exemplo, uma malha com uma abertura de 1 mm será mais pesada do que uma malha com uma abertura de 5 mm, partindo do princípio de que o diâmetro dos fios e o número de malhas são os mesmos.
Tipo de material: Diferentes materiais têm diferentes densidades, o que afecta diretamente o peso. Os materiais mais comuns incluem o aço inoxidável, o aço macio, o alumínio, o latão e o cobre. Por exemplo, o aço inoxidável tem uma densidade de aproximadamente 7,93 g/cm³, enquanto o alumínio tem uma densidade de cerca de 2,70 g/cm³. Isto significa que, para o mesmo volume, o aço inoxidável será significativamente mais pesado do que o alumínio.
Dimensões: A largura e o comprimento do rolo ou do painel de rede metálica também têm impacto no peso total. Estes são normalmente medidos em metros ou pés. Por exemplo, um painel de rede metálica com 10 metros por 1 metro pesará mais do que um painel com 5 metros por 1 metro, se todos os outros factores forem idênticos.
Basta introduzir a largura, o comprimento, a largura da malha, o comprimento da malha, o diâmetro da malha de arame na calculadora abaixo e obterá o resultado do peso da malha de arame em kg e libras.
O cálculo do peso da rede metálica é essencial. Garante um planeamento preciso em vários projectos industriais e de construção. O cálculo do peso depende do diâmetro do fio, do número de malhas, da densidade do material e das dimensões.
O método de cálculo do peso da rede de arame pode ser determinado de várias formas, dependendo do material, da estrutura da rede de arame e dos parâmetros específicos necessários para o cálculo. Podemos resumir vários métodos de cálculo diferentes e factores a considerar.
Em primeiro lugar, um método básico de cálculo do peso consiste em efetuar uma estimativa dividindo o produto do diâmetro do fio, da contagem de malhas, do comprimento da malha e da largura da malha por 2. Este método é aplicável aos cálculos gerais do peso da malha de arame, em que a unidade do diâmetro do fio é o milímetro (mm) e as unidades do comprimento e da largura da malha são o metro (m).
Além disso, para tipos específicos de rede de arame, como a rede de arame galvanizado, podem ser utilizados métodos de cálculo mais pormenorizados. Por exemplo, o peso da rede de arame galvanizado pode ser calculado medindo o comprimento do arame por metro quadrado (em metros) e o peso do arame por metro (em quilogramas). Este método proporciona uma forma direta de estimar o peso da rede de arame.
Outro método consiste em calcular o peso através da área da secção transversal e do comprimento do fio, bem como da densidade do material. Isto pode ser conseguido através da fórmula "Peso (kg) = Área da secção transversal (mm2) × Comprimento(m) × Densidade(g/cm3) × 1/1000″. Este método é adequado para situações em que é necessário um cálculo exato do peso da malha de arame, especialmente quando se considera a densidade de diferentes materiais.
A seguinte fórmula simplificada pode ser utilizada para calcular o peso da rede de arame de aço.
Peso (kg) = comprimento total das matérias-primas * diâmetro do fio² * coeficiente (0,00617)
Rede metálica de aço inoxidável
O aço inoxidável é normalmente utilizado pela sua resistência à corrosão e força. Para rede metálica de aço inoxidável:
Malha de arame de aço macio
O aço macio é conhecido pela sua durabilidade e acessibilidade. O cálculo da rede metálica de aço macio é semelhante ao do aço inoxidável, mas utiliza um fator de densidade diferente:
Rede de arame de alumínio
O alumínio é valorizado pelas suas propriedades de leveza e resistência à corrosão. Para redes de arame de alumínio:
Malha de arame de latão e cobre
O latão e o cobre são utilizados devido à sua excelente condutividade eléctrica e estética. Para estes materiais:
Para latão:
Para o cobre:
Para ilustrar, vamos calcular o peso de uma rede de arame de aço inoxidável com as seguintes especificações:
Utilizando a fórmula geral:
Para aço inoxidável:
Para o peso total:
Ao compreender estes factores e aplicar as fórmulas adequadas, é possível obter cálculos precisos do peso da rede metálica, garantindo um planeamento e uma execução precisos em vários projectos.
A tabela seguinte apresenta o peso teórico da rede de arame de aço em kg/m². Se a sua dimensão de aço não constar da tabela abaixo, pode utilizar o nosso calculadora de peso do aço para calcular em linha.
(1) Reforço longitudinal peso da barra gráfico
| Grau | Varão de reforço longitudinal | Peso teórico | ||
| Dia. | Distância | Área por metro linear | ||
| (mm) | (mm) | (mm²/m) | (kg/m²) | |
| A18 | 18 | 200 | 1273 | 14.43 |
| A16 | 16 | 200 | 1006 | 12.34 |
| A14 | 14 | 200 | 770 | 10.49 |
| A12 | 12 | 200 | 566 | 8.88 |
| A11 | 11 | 200 | 475 | 7.46 |
| A10 | 10 | 200 | 393 | 6.16 |
| A9 | 9 | 200 | 318 | 4.99 |
| A8 | 8 | 200 | 252 | 3.95 |
| A7 | 7 | 200 | 193 | 3.02 |
| A6 | 6 | 200 | 142 | 2.22 |
| A5 | 5 | 200 | 98 | 1.54 |
| B18 | 18 | 100 | 2545 | 24.42 |
| B16 | 16 | 100 | 2011 | 18.89 |
| B14 | 14 | 100 | 1539 | 15.19 |
| B12 | 12 | 100 | 1131 | 10.9 |
| B11 | 11 | 100 | 950 | 9.43 |
| B10 | 10 | 100 | 785 | 8.14 |
| B9 | 9 | 100 | 635 | 6.97 |
| B8 | 8 | 100 | 503 | 5.93 |
| B7 | 7 | 100 | 385 | 4.53 |
| B6 | 6 | 100 | 283 | 3.73 |
| B5 | 5 | 100 | 196 | 3.05 |
| C18 | 18 | 150 | 1697 | 17.77 |
| C16 | 16 | 150 | 1341 | 14.98 |
| C14 | 14 | 150 | 1027 | 12.51 |
| C12 | 12 | 150 | 754 | 10.36 |
| C11 | 11 | 150 | 634 | 8.7 |
| C10 | 10 | 150 | 523 | 7.19 |
| C9 | 9 | 150 | 423 | 5.82 |
| C8 | 8 | 150 | 335 | 4.61 |
| C7 | 7 | 150 | 257 | 3.53 |
| C6 | 6 | 150 | 189 | 2.6 |
| C5 | 5 | 150 | 131 | 1.8 |
| D18 | 18 | 100 | 1545 | 28.86 |
| D16 | 16 | 100 | 2011 | 24.68 |
| D14 | 14 | 100 | 1539 | 20.98 |
| D12 | 12 | 100 | 1131 | 17.75 |
| D11 | 11 | 100 | 950 | 14.92 |
| D10 | 10 | 100 | 785 | 12.33 |
| D9 | 9 | 100 | 635 | 9.98 |
| D8 | 8 | 100 | 503 | 7.9 |
| D7 | 7 | 100 | 385 | 6.04 |
| D6 | 6 | 100 | 283 | 4.44 |
| D5 | 5 | 100 | 196 | 3.08 |
| E18 | 18 | 150 | 1697 | 19.25 |
| E16 | 16 | 150 | 1341 | 16.46 |
| E14 | 14 | 150 | 1027 | 13.99 |
| E12 | 12 | 150 | 754 | 11.84 |
| E11 | 11 | 150 | 634 | 9.95 |
| E10 | 10 | 150 | 523 | 8.22 |
| E9 | 9 | 150 | 423 | 6.66 |
| E8 | 8 | 150 | 335 | 5.26 |
| E7 | 7 | 150 | 257 | 4.03 |
| E6 | 6 | 150 | 189 | 2.96 |
| E5 | 5 | 150 | 131 | 2.05 |
| F18 | 18 | 100 | 2545 | 25.9 |
| F16 | 16 | 100 | 2011 | 21.7 |
| F14 | 14 | 100 | 1539 | 18 |
| F12 | 12 | 100 | 1131 | 14.8 |
| F11 | 11 | 100 | 950 | 12.43 |
| F10 | 10 | 100 | 785 | 10.28 |
| F9 | 9 | 100 | 635 | 8.32 |
| F8 | 8 | 100 | 503 | 6.58 |
| F7 | 7 | 100 | 385 | 5.03 |
| F6 | 6 | 100 | 283 | 3.7 |
| F5 | 5 | 100 | 196 | 2.57 |
(2) Tabela de pesos dos varões de reforço transversais
| Grau | Varão de reforço transversal | Peso teórico | ||
| Dia. | Distância | Área por metro linear | ||
| (mm) | (mm) | (mm²/m) | (kg/m²) | |
| A18 | 12 | 200 | 566 | 14.43 |
| A16 | 12 | 200 | 566 | 12.34 |
| A14 | 12 | 200 | 566 | 10.49 |
| A12 | 12 | 200 | 566 | 8.88 |
| A11 | 11 | 200 | 475 | 7.46 |
| A10 | 10 | 200 | 393 | 6.16 |
| A9 | 9 | 200 | 318 | 4.99 |
| A8 | 8 | 200 | 252 | 3.95 |
| A7 | 7 | 200 | 193 | 3.02 |
| A6 | 6 | 200 | 142 | 2.22 |
| A5 | 5 | 200 | 98 | 1.54 |
| B18 | 12 | 200 | 566 | 24.42 |
| B16 | 10 | 200 | 393 | 18.89 |
| B14 | 10 | 200 | 393 | 15.19 |
| B12 | 8 | 200 | 252 | 10.9 |
| B11 | 8 | 200 | 252 | 9.43 |
| B10 | 8 | 200 | 252 | 8.14 |
| B9 | 8 | 200 | 252 | 6.97 |
| B8 | 8 | 200 | 252 | 5.93 |
| B7 | 7 | 200 | 193 | 4.53 |
| B6 | 7 | 200 | 193 | 3.73 |
| B5 | 7 | 200 | 193 | 3.05 |
| C18 | 12 | 200 | 566 | 17.77 |
| C16 | 12 | 200 | 566 | 14.98 |
| C14 | 12 | 200 | 566 | 12.51 |
| C12 | 12 | 200 | 566 | 10.36 |
| C11 | 11 | 200 | 475 | 8.7 |
| C10 | 10 | 200 | 393 | 7.19 |
| C9 | 9 | 200 | 318 | 5.82 |
| C8 | 8 | 200 | 252 | 4.61 |
| C7 | 7 | 200 | 193 | 3.53 |
| C6 | 6 | 200 | 142 | 2.6 |
| C5 | 5 | 200 | 98 | 1.8 |
| D18 | 12 | 100 | 1131 | 28.86 |
| D16 | 12 | 100 | 1131 | 24.68 |
| D14 | 12 | 100 | 1131 | 20.98 |
| D12 | 12 | 100 | 1131 | 17.75 |
| D11 | 11 | 100 | 950 | 14.92 |
| D10 | 10 | 100 | 785 | 12.33 |
| D9 | 9 | 100 | 635 | 9.98 |
| D8 | 8 | 100 | 503 | 7.9 |
| D7 | 7 | 100 | 385 | 6.04 |
| D6 | 6 | 100 | 283 | 4.44 |
| D5 | 5 | 100 | 196 | 3.08 |
| E18 | 12 | 150 | 754 | 19.25 |
| E16 | 12 | 150 | 754 | 16.46 |
| E14 | 12 | 150 | 754 | 13.99 |
| E12 | 12 | 150 | 754 | 11.84 |
| E11 | 11 | 150 | 634 | 9.95 |
| E10 | 10 | 150 | 523 | 8.22 |
| E9 | 9 | 150 | 423 | 6.66 |
| E8 | 8 | 150 | 335 | 5.26 |
| E7 | 7 | 150 | 257 | 4.03 |
| E6 | 6 | 150 | 189 | 2.96 |
| E5 | 5 | 150 | 131 | 2.05 |
| F18 | 12 | 150 | 754 | 25.9 |
| F16 | 12 | 150 | 754 | 21.7 |
| F14 | 12 | 150 | 754 | 18 |
| F12 | 12 | 150 | 754 | 14.8 |
| F11 | 11 | 150 | 634 | 12.43 |
| F10 | 10 | 150 | 523 | 10.28 |
| F9 | 9 | 150 | 423 | 8.32 |
| F8 | 8 | 150 | 335 | 6.58 |
| F7 | 7 | 150 | 257 | 5.03 |
| F6 | 6 | 150 | 189 | 3.7 |
| F5 | 5 | 150 | 131 | 2.57 |
Os cálculos exactos do peso da malha de arame são essenciais para várias aplicações, desde a construção até ao fabrico. Compreender os factores que influenciam estes cálculos garante precisão e fiabilidade, que são cruciais para um planeamento eficaz e uma estimativa de custos.
O diâmetro do fio, medido em milímetros (mm), tem um impacto significativo no peso da rede de arame. O peso aumenta com o quadrado do diâmetro do fio. Por exemplo, se um fio com um diâmetro de 2 mm pesa 1 kg por metro, um fio com um diâmetro de 4 mm pesará 4 kg por metro, assumindo que os outros factores se mantêm constantes. Esta relação exponencial sublinha a importância de medições precisas do diâmetro do fio.
A contagem de malhas refere-se ao número de aberturas por polegada na malha de arame. Um maior número de malhas significa mais fios numa determinada área, aumentando o peso total. Por exemplo, uma malha de arame de 20 malhas (20 aberturas por polegada) pesará mais do que uma malha de arame de 10 malhas (10 aberturas por polegada) com o mesmo diâmetro de arame. A contagem das malhas influencia diretamente a densidade e o peso da malha.
As dimensões do rolo de rede metálica, incluindo o comprimento e a largura, têm um impacto significativo no peso total. Estas dimensões são normalmente medidas em metros ou pés. Por exemplo, um rolo de rede de arame com 10 metros de comprimento e 1 metro de largura pesará mais do que um rolo com 5 metros por 1 metro, assumindo o mesmo diâmetro de arame e número de malhas. As medições exactas das dimensões do rolo são essenciais para calcular o peso total.
As tolerâncias de fabrico podem introduzir variações no diâmetro do fio, no número de malhas e nas dimensões do rolo. Estas variações podem afetar os cálculos de peso, conduzindo a discrepâncias entre os pesos calculados e os pesos reais. Tenha em conta as potenciais variações e tolerâncias de fabrico para garantir a exatidão.
Os diferentes materiais têm densidades distintas, afectando diretamente o peso da rede metálica. Os materiais mais comuns incluem o aço inoxidável, o aço macio, o alumínio, o latão e o cobre, cada um com a sua densidade específica. Por exemplo, o aço inoxidável tem uma densidade de aproximadamente 7,93 g/cm³, enquanto o alumínio tem uma densidade de cerca de 2,70 g/cm³. Ajustar a fórmula do peso geral para incorporar a densidade específica do material para obter cálculos precisos.
A rede de arame pode ser revestida com materiais como o zinco (galvanizado), PVC ou outros revestimentos de proteção para aumentar a durabilidade e a resistência à corrosão. Estes revestimentos aumentam o peso total da malha de arame. Por exemplo, a malha de arame galvanizado pesará mais do que a malha de arame sem revestimento devido à camada adicional de zinco. Considere o peso dos revestimentos ao efetuar os cálculos.
Os tratamentos térmicos, como o recozimento ou o endurecimento, podem alterar as propriedades físicas da malha de arame, afectando potencialmente o seu peso. Embora o impacto no peso possa ser mínimo, continua a ser importante ter em conta quaisquer alterações nas propriedades do material resultantes de tratamentos térmicos.
As variações de temperatura podem provocar a expansão ou contração térmica da rede metálica, afectando as suas dimensões e peso. Por exemplo, as temperaturas elevadas podem provocar a expansão da rede metálica, levando a um ligeiro aumento do peso por unidade de área. Considerar as condições de temperatura de funcionamento ao calcular o peso para aplicações específicas.
A humidade pode afetar o peso de certos materiais de rede metálica, particularmente os que são propensos à corrosão ou à oxidação. Por exemplo, a rede de arame de aço macio não revestido pode absorver a humidade do ambiente, aumentando o seu peso ao longo do tempo. A consideração da humidade ambiental é crucial para aplicações em que a rede metálica está exposta a níveis de humidade variáveis.
Compreender e ter em conta estes factores garante cálculos precisos do peso da rede metálica, ajudando a um planeamento preciso, a uma estimativa de custos e a uma execução eficiente do projeto.
Seguem-se as respostas a algumas perguntas frequentes:
Para calcular o peso da rede metálica de aço inoxidável, é necessário ter em conta o diâmetro do fio, o número da malha (número de malhas por polegada) e as dimensões do painel de malha. Eis os passos e as fórmulas para os diferentes tipos de malha:
Para a rede de arame soldado de aço inoxidável com furo quadrado, a fórmula é:
Em alternativa, pode utilizar:
Por exemplo, se tiver uma rede de arame de aço inoxidável com um diâmetro de fio de 0,12 mm, um número de malha de 80 por polegada e dimensões de 1 metro por 30 metros:
Para a rede de arame soldado de aço inoxidável com orifício retangular, a fórmula é:
Uma fórmula geral aplicável a qualquer forma é:
Por exemplo, para uma rede de arame soldado galvanizado com um diâmetro de fio de 0,9 mm, um tamanho de malha de 1/2 polegada x 1/2 polegada e dimensões de 3 pés por 100 pés:
Pontos-chave a reter:
Utilizando estas fórmulas e assegurando que todas as medidas estão nas unidades corretas, pode calcular com precisão o peso da rede metálica de aço inoxidável para as suas necessidades específicas.
A precisão dos cálculos do peso da malha de arame é influenciada por vários factores-chave. Em primeiro lugar, o diâmetro do fio é crucial, uma vez que quaisquer imprecisões na sua medição podem afetar significativamente o peso total. É essencial uma medição exacta utilizando ferramentas como um paquímetro ou um micrómetro. Em segundo lugar, a contagem da malha, que indica o número de orifícios por polegada, e o tamanho da abertura, ou o espaço entre os fios, são parâmetros críticos. Estes factores determinam a densidade e a área aberta da malha, afectando assim o seu peso. São necessárias medições precisas destes parâmetros para efetuar cálculos exactos.
Além disso, o comprimento e a largura da malha devem ser medidos com precisão, uma vez que têm um impacto direto no cálculo do peso. A densidade do material também desempenha um papel importante; diferentes materiais, como o aço inoxidável ou o cobre, têm densidades diferentes que devem ser tidas em conta no cálculo. A utilização da fórmula correta para o cálculo do peso é vital, sendo necessárias fórmulas diferentes para a malha de arame liso/tecido sarjado e para a malha de arame holandesa.
A precisão da medição em todos os parâmetros - diâmetro do fio, contagem de malhas, comprimento e largura - é crucial para evitar erros que possam levar a imprecisões. Por último, os factores ambientais e de manuseamento, tais como deformações ou danos devidos a armazenamento ou manuseamento inadequados, podem afetar indiretamente os cálculos do peso, alterando as dimensões da malha. Tendo em conta estes factores e utilizando medições exactas e fórmulas adequadas, o peso da malha de arame pode ser calculado com elevada precisão.
O diâmetro do fio influencia significativamente o peso da malha de arame através de vários factores-chave. Em primeiro lugar, o peso da malha de arame é diretamente proporcional ao quadrado do diâmetro do arame. Isto significa que, à medida que o diâmetro do fio aumenta, o peso da malha aumenta exponencialmente. A relação pode ser representada pela fórmula: Peso = (diâmetro do fio)² x malha x comprimento x largura. Esta fórmula evidencia que o peso é uma função do diâmetro do fio ao quadrado, indicando um aumento substancial do peso mesmo com pequenos aumentos de diâmetro.
Um diâmetro de fio mais grosso resulta numa malha mais forte e mais durável, mas também reduz o tamanho das aberturas entre os fios. Este aumento do volume de material contribui para um peso total mais elevado. A medição exacta do diâmetro do fio, normalmente utilizando um micrómetro ou um paquímetro, é crucial, uma vez que afecta diretamente o cálculo do peso.
O tamanho da abertura, que é a distância entre dois fios adjacentes, é determinado subtraindo o diâmetro do fio do passo (a distância entre os centros de dois fios adjacentes). Embora o tamanho da abertura em si não calcule o peso, é influenciado pelo diâmetro do fio, que por sua vez afecta o peso.
Em termos práticos, os fios mais grossos requerem mais material, o que leva a um aumento do peso total da malha. Isto é particularmente importante em aplicações em que o peso é um fator crítico, como nas indústrias aeroespacial ou da construção. Além disso, as tolerâncias padrão para os diâmetros dos fios podem causar variações no peso final da malha. Por exemplo, os intervalos de tolerância específicos para a malha de arame de aço inoxidável podem afetar o peso final.
Em conclusão, o diâmetro do fio é um parâmetro crucial que tem um impacto direto no peso da malha de arame. À medida que o diâmetro do fio aumenta, o peso da rede também aumenta devido ao maior volume de material utilizado, aumentando a resistência e a durabilidade da rede.
Sim, é possível calcular o peso da malha de arame para diferentes materiais utilizando uma fórmula geral, mas é necessário efetuar ajustes específicos ao material para garantir a precisão. A fórmula geral para calcular o peso da malha de arame envolve normalmente parâmetros como o diâmetro do arame, o número da malha (número de malhas por polegada), a largura e o comprimento da malha.
A fórmula básica é:
Esta fórmula é geralmente aplicável a materiais como o aço inoxidável, o ferro e o aço. No entanto, para outros metais como o alumínio, o latão, o cobre, o aço macio, o níquel e o bronze fosforoso, é necessário ajustar o peso calculado multiplicando-o por factores específicos de cada material. Por exemplo, o peso do alumínio é ajustado multiplicando-o por 0,364 e o do latão por 1,094.
Além disso, o tipo de malha pode afetar o cálculo. Para malhas com furos quadrados, o cálculo é simples, utilizando a fórmula acima. Para a malha de orifícios rectangulares, é necessário ter em conta os números da malha de urdidura e da trama e os diâmetros dos fios.
Para ilustrar, se calcular o peso da malha de aço inoxidável como 17,28 kg, para o alumínio, seria:
17,28 kg x 0,364=6,29 kg
Em resumo, embora a fórmula principal para calcular o peso da malha de arame seja semelhante em diferentes materiais, é necessário ter em conta as densidades específicas do material e os factores de ajustamento necessários. Além disso, o tipo de malha (furos quadrados ou rectangulares) pode influenciar o cálculo. Por conseguinte, os ajustamentos específicos do material e as considerações sobre o tipo de malha são essenciais para cálculos de peso exactos.
A influência do material de uma rede de arame no seu peso manifesta-se principalmente na densidade dos diferentes materiais. Os materiais dos cabos e das redes de arame podem ser divididos em arame de aço, aço de níquel-crómio, aço de liga, aço inoxidável, etc. Estes materiais têm densidades diferentes, afectando assim o seu peso.
Por exemplo, uma rede de arame feita de arame de aço, que apresenta uma excelente resistência e durabilidade, é adequada para suportar tensões e pressões consideráveis, sendo amplamente aplicada na indústria da construção.
Além disso, os materiais das malhas de proteção incluem geralmente fio de aço, liga de alumínio, aço inoxidável, etc. A diferença de densidade destes materiais resultaria também em pesos diferentes. Assim, pode concluir-se que o impacto do material de uma rede de proteção no seu peso se deve principalmente às diferenças de densidade dos vários materiais.
A seleção do método de cálculo adequado depende do tipo de malha de arame, como a malha de arame galvanizado, a malha de arame de aço inoxidável, etc. Podemos resumir OS seguintes pontos:
Para os diferentes tipos de malhas de arame, as fórmulas de cálculo do peso podem variar. Este facto indica que é necessário ter em conta nos cálculos as propriedades específicas dos diferentes materiais das malhas de arame.
O cálculo das peças de malha de arame pode ser efectuado por um software que calcula automaticamente o comprimento de acordo com o material, multiplicando-o depois pela largura especificada no projeto. Este método é aplicável a redes de arame de vários materiais, incluindo, mas não se limitando a, redes de arame galvanizado e redes de arame de aço inoxidável.
Em termos de soldadura de construção, o método de cálculo das especificações das peças de malha de arame reflecte-se na produção de vários modelos, tamanhos e tipos de estilo. Isto significa que, ao selecionar o método de cálculo, é necessário ter em conta as especificações específicas e os requisitos de aplicação da rede de arame.
A escolha do método de cálculo adequado requer, em primeiro lugar, a compreensão do tipo e das características da rede de arame. Para a rede de arame galvanizado e a rede de arame de aço inoxidável, etc., o método de software que calcula automaticamente o comprimento e multiplica pela largura pode ser utilizado para o cálculo. Isto assegura a exatidão e a aplicabilidade dos resultados do cálculo.
Nas aplicações do mundo real, a escolha do método mais adequado para calcular o peso da malha de arame exige que se considere primeiro o tipo específico de malha e a sua utilização. Podemos verificar que os diferentes tipos de malha têm fórmulas de cálculo diferentes. Por exemplo, as fórmulas de cálculo do peso da malha de cobre e da malha de aço inoxidável são as seguintes:
Fórmula de cálculo do peso da rede de cobre: Diâmetro do fio × diâmetro do fio × número de malhas × comprimento × largura ÷ 2 × 1,07 = kg.
Fórmula de cálculo do peso da rede de aço inoxidável: Diâmetro do fio × Diâmetro do fio × Número de malhas × Comprimento × Largura ÷ 2 × 1,07 = kg.
Isto mostra que os métodos de cálculo para a malha de cobre e a malha de aço inoxidável são semelhantes, sendo a principal diferença a diferença de densidade (1,07) causada pelos diferentes materiais.
Para a malha de chapa de alumínio e aço, a fórmula de cálculo do peso é a seguinte
Peso da malha (kg): Comprimento da malha ÷ 1/2 retângulo de secção curta × Espessura do caule × Largura do caule × Largura da malha × 7,85.
Esta fórmula envolve vários parâmetros, tais como o comprimento da malha, o retângulo de secção curta (largura do orifício), a espessura da haste, a largura da haste e a largura da malha, e é adequada para calcular com precisão áreas maiores ou estruturas complexas de malhas de arame.
Por conseguinte, ao escolher o método de cálculo de peso mais adequado, deve ser decidido de acordo com o tipo específico de malha de arame e a sua utilização. Se se tratar de uma rede de cobre ou de uma rede de aço inoxidável, pode ser utilizada a fórmula geral de cálculo acima referida. Para tipos especiais de malha, como a malha de chapa de alumínio e aço, deve ser utilizada uma fórmula de cálculo especificamente concebida para esse tipo de malha. Além disso, as considerações relativas ao cálculo dos custos, tais como o custo:= peso da malha × preço da placa + custo da mão de obra + custo da circulação, são também um dos factores a ter em conta na escolha de um método de cálculo.