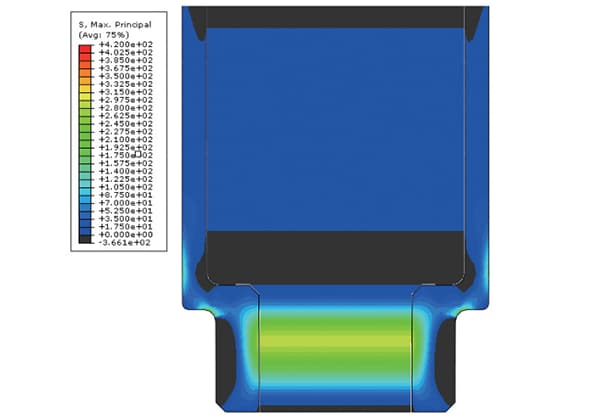
Imagine saber exatamente quanta tensão os seus componentes metálicos podem suportar sem os cortar. A medição de tensões residuais por raios X oferece este conhecimento através da utilização de métodos de ensaio não destrutivos. Este artigo explora como as técnicas de difração de raios X medem com precisão as tensões internas, aumentando a fiabilidade e a longevidade do produto. Saiba como diferentes métodos, como as técnicas sin²ψ e cosα, fornecem dados de tensão precisos, garantindo que a sua metalurgia cumpre os mais elevados padrões. Mergulhe nessas técnicas avançadas de medição para entender seus princípios, aplicações e benefícios para a engenharia industrial.
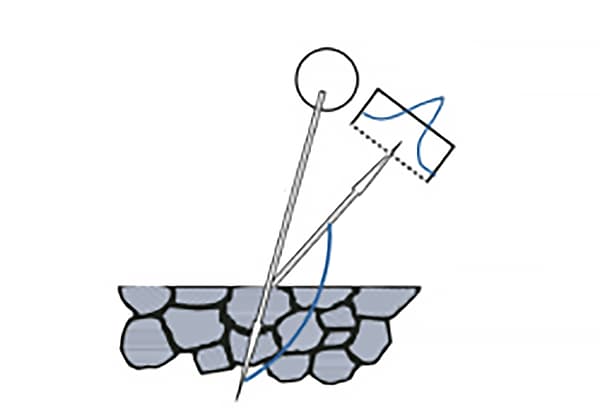
A tensão residual é um tipo de tensão interna referida como tal na engenharia. A distribuição da tensão residual numa peça de trabalho é frequentemente irregular, o que pode afetar significativamente a sua resistência estática, resistência à fadiga, estabilidade da forma e resistência à corrosão. Como resultado, a medição da tensão residual é crucial.
Existem dois métodos principais de medição tensão residualO método de ensaio é o seguinte: ensaio destrutivo e ensaio não destrutivo. O método de ensaio destrutivo consiste em remover uma porção da peça e calcular o tensão residual com base na deformação e no deslocamento correspondentes. Os métodos comuns de ensaio destrutivo incluem perfuração e método do núcleo em anel.
O método de ensaio não destrutivo envolve o estabelecimento de uma relação entre a tensão residual e uma quantidade física que pode causar uma alteração no material (como o espaçamento do plano cristalino, a taxa de propagação de ondas ultra-sónicas ou a permeabilidade magnética) para calcular a tensão residual. Os métodos de ensaio não destrutivos incluem a difração de raios X, a difração de neutrões, os métodos magnéticos e ultra-sónicos.
A difração de raios X é o método mais utilizado para a medição de tensões residuais, devido aos seus princípios maduros e métodos bem estabelecidos, bem como à disponibilidade de equipamento de ensaio cada vez mais sofisticado, incluindo instrumentos de laboratório, instrumentos portáteis para medição no terreno e dispositivos especializados para circunstâncias especiais.
O método de difração de raios X para medir a tensão residual foi proposto pela primeira vez pelo académico russo Akchenov em 1929 e equiparou a tensão macroscópica à tensão da rede. Em 1961, o académico alemão Macherauch desenvolveu ainda mais o método de sin2ψ baseado na ideia de Akchenov, tornando a medição da tensão residual por difração de raios X uma tecnologia fiável e amplamente utilizada.
Ao longo dos últimos 60 anos, a difração de raios X desenvolveu-se em vários métodos de medição diferentes, com sin2O método ψ e o método cosα são os dois principais métodos atualmente utilizados.
Para dominar a tecnologia de difração de raios X para medir a tensão residual, é importante compreender os seus vários métodos.
(1) Os métodos de medição das tensões residuais por difração de raios X podem ser classificados em duas abordagens principais: a sin2método ψ e o método cosα.
(2) O pecado2O método ψ pode ainda ser classificado com base no método de cálculo da tensão residual, no método 2θ, no método do valor d e no método da deformação.
(3) Com base na relação geométrica entre ψ e 2θ, o sen2O método ψ pode ser dividido em dois tipos: o método de co-tilt e o método de roll.
(4) O método de medição pode também ser diferenciado com base no modo de varrimento do tubo de raios X e do contra-tubo, no método do ψ0 fixo e no método do ψ fixo.
(5) No âmbito do método do rolo, existem três subcategorias: o método do rolo normal, o método do rolo modificado e o método de fixação do rolo ψ.
(6) O método de medição ψ positivo e negativo é utilizado para determinar a tensão de cisalhamento τφ.
(7) A difração de raios X é normalmente utilizada para medir a tensão numa direção específica num determinado ponto, mas também existem métodos para medir a tensão principal num ponto.
(8) O método de oscilação pode ser dividido em várias subcategorias: o método de oscilação ψ0, o método de oscilação ψ, o método de oscilação do anel de Debye, o método de oscilação do ângulo φ e o método de translação recíproca X/Y.
(9) Em termos de geometria de difração, existem três abordagens: o método de focalização, o método de quase-focalização e o método do feixe paralelo.
A tensão é determinada pela deformação. No caso de materiais policristalinos, a tensão residual é estimada pelo resultado estatístico da deformação da rede na região relevante.
Assim, a tensão residual pode ser determinada medindo a deformação da rede através da técnica de difração de raios X.
A tensão residual do material reflecte a macro deformação.
A macro deformação é equivalente à deformação da rede.
A deformação da rede representa a alteração relativa do espaçamento entre os planos cristalinos, que pode ser calculada utilizando um dispositivo de difração baseado na lei de Bragg.
Isto resume o método de difração de raios X para medir a tensão residual.
Quando um policristal é exposto a um feixe de raios X com um comprimento de onda específico (λ), a intensidade máxima dos raios X reflectidos (ou seja, o pico de difração) será observada num ângulo de difração específico (2θ), como ilustrado na Figura 1. Este fenómeno é conhecido como difração de raios X.
A relação entre o comprimento de onda dos raios X (λ), o espaçamento entre planos cristalinos (d) e o ângulo de Bragg (θ) é descrita pela seguinte equação (1).

Na análise de difração de raios X da tensão residual, o material alvo apropriado para o tubo de raios X é selecionado para determinar o comprimento de onda adequado (λ). O ângulo de difração (2θ) é então medido utilizando um dispositivo de difração. Com base na medição, pode ser calculado o espaçamento do plano cristalino (d) do plano cristalino relevante.

Fig. 1 Geometria da difração de raios X
De acordo com a lei da reflexão da ótica, a normal do plano cristalino envolvida na difração tem de se situar na bissetriz entre os raios recebidos e reflectidos, como ilustrado na Figura 2.
O ângulo entre a normal do plano do cristal de difração e a normal da superfície da amostra é conhecido como o ângulo azimutal da normal do plano do cristal de difração, que é normalmente representado por ψ.

Fig. 2 Diagrama esquemático do plano cristalino de difração de raios X Azimute ψ
A lei de Bragg permite a determinação do espaçamento (dψ) dos planos cristalinos numa orientação específica (ψ).
Se o espaçamento (d0) dos planos cristalinos no estado livre de tensão for conhecido, a deformação da rede (εψ) na orientação designada pode ser calculada.
S1, S2 e S3 são os eixos da superfície do provete e S1 é definido pelo investigador.
A Figura 3 ilustra o sistema de coordenadas utilizado para medir a tensão residual através da difração de raios X.

Fig. 3 Sistema de coordenadas para a medição de tensões por difração de raios X
De acordo com a lei de Hooke generalizada, as deformações desses planos cristalinos são influenciadas pelo tensor de tensão no ponto O e estão intimamente ligadas ao seno e cosseno de φ e ψ, ao módulo de Young do material e ao coeficiente de Poisson.
Assim, é possível determinar a tensão tridimensional no ponto O, incluindo a tensão (σφ).
A expressão para a deformação na direção OP pode ser derivada da teoria da elasticidade.
Para a maioria dos materiais e componentes, a profundidade de penetração dos raios X é apenas de alguns microns a dezenas de microns, pelo que se assume normalmente que σ33=0.
Por conseguinte, a deformação na direção OP é representada pela equação (2).


O pecado2A fórmula do método ψ é derivada com base na lei de Bragg e na teoria elástica.
Os objectos considerados na teoria da elasticidade são assumidos como meios homogéneos, contínuos e isotrópicos.
No entanto, este pressuposto só é válido para os materiais policristalinos materiais metálicos se a granulometria for fina e não houver textura.
A Fig. 4 mostra a curva da relação funcional de εn e o pecado2ψ para materiais isotrópicos, materiais com gradiente de tensão ou gradiente de composição, materiais com tensão de cisalhamento e materiais anisotrópicos com textura.

Como mostra a Fig. 4c), se a tensão de cisalhamento τ13≠ 0, τ23≠0 e sin2A curva ψ tem ± ψ bifurcação, σφ e τφ pode ser obtido utilizando os dados de deformação medidos ε﹢ψ e ε-ψ numa série de ângulos de ± ψ, como indicado nas Fórmulas (4) e (5).

É importante notar que o pecado2ψ mostrada na Figura 4c) não é suscetível de ter uma bifurcação ±ψ.
Isto deve-se ao facto de os raios X utilizados para a difração terem uma profundidade de penetração limitada no material testado, normalmente apenas alguns microns a dezenas de microns.
Consequentemente, as componentes de tensão perpendiculares à superfície do material podem ser consideradas como zero.
Somente quando o plano de tensão principal se desvia da superfície do espécime sob a condição de usinagem especial (como retificação poderosa e de grande quantidade de corte) pode τ13≠0 e τ23≠0 ocorrem.
A bifurcação ±ψ não é uma ocorrência comum, e a curva de ajuste carece frequentemente do atributo de elipse. Isto deve-se em grande parte ao erro sistemático no mecanismo ±ψ do goniómetro. Por conseguinte, não é necessário realçar demasiado a importância da adaptação da elipse.
Em conclusão, o processo prático e implementável de determinar a tensão residual através da difração de raios X envolve a seleção de alguns ângulos ψ (ou vários pares de ângulos ±ψ) e a medição do ângulo de difração correspondente (2θφψ), seguido de cálculo.
Os estudiosos desenvolveram vários métodos para organizar a relação geométrica espacial entre o plano ψ e o plano 2θ, determinar a curva de difração e efetuar cálculos.
O ângulo de difração 2θφψ é medido pelo dispositivo de difração de raios X, e o correspondente espaçamento do plano cristalino é calculado como dφψ de acordo com a lei de Bragg, então a deformação da rede εφψ pode ser expressa pelo espaçamento do plano cristalino, como se mostra na Fórmula (6).

A deformação verdadeira é diretamente substituída na Equação (3), na Equação (4) e na Equação (5) para calcular a tensão, que é a expressão do método da deformação verdadeira.
É adotado o método da deformação real, e os valores exactos de d0 e θ0 não são necessárias.
Na maioria dos casos, o método da deformação real tem vantagens significativas.
Também podem ser utilizadas equações aproximadas para calcular a deformação, como mostram as Eq. (7) e Eq. (8).

A fórmula de cálculo do método 2θ é apresentada na equação (9).

Onde, K é a constante de tensão, e a sua fórmula de cálculo é apresentada na equação (10).

Onde: ν é o coeficiente de Poisson do material.
Para alguns materiais, θ0 varia muito com a composição química, e os resultados terão um grande desvio se for utilizada a constante de tensão.
O método de deformação real foi incluído na norma da União Europeia EN 15305-2008 Ensaios não destrutivos - Método de ensaio para análise de tensões residuais por difração de raios X e GB/T 7704-2017 Ensaios não destrutivos - Método de medição de tensões por raios X.
O medidor de tensão doméstico XL-640 lista o método de deformação verdadeira como o método de cálculo de tensão predefinido e o método 2θ pode ser selecionado para cálculo.
O método coplanar é um método de medição em que o plano 2θ coincide com o plano ψ (plano da direção da tensão), como se mostra na Fig. 5.

Fig. 5 Diagrama geométrico do mesmo método de inclinação
Com o mesmo método de inclinação, o ângulo de incidência dos raios X ψ0 é dominante, enquanto o ângulo ψ pode ser calculado, como mostram as Eq. (11) e Eq. (12).

No ensaio de esforço da peça de trabalho real, quando o ponto de ensaio está localizado numa ranhura pouco profunda semelhante, o espaço de ensaio do goniómetro é limitado, pelo que o mesmo método de inclinação é mais adequado.
O método do rolo é um método de medição em que o plano 2θ e o plano ψ (plano da direção da tensão) são perpendiculares um ao outro, como se mostra na Fig. 6.

Fig. 6 Diagrama geométrico do método do rolo
A principal caraterística do método Roll (método χ) é o seu pequeno fator de absorção do pico de difração, que contribui para uma maior precisão da medição.
As gamas 2θ e ψ podem ser totalmente alargadas conforme necessário. Para determinados materiais, os raios difractivos com posições de pico baixas (tais como picos abaixo de 145°) podem ser utilizados para a medição de tensões.
No entanto, o plano 2θ e o plano ψ deste método são perpendiculares entre si, exigindo um espaço tridimensional, o que torna difícil a sua aplicação à medição de espaços estreitos.
Um instrumento de medição de tensões de uma empresa estrangeira utiliza um método Roll modificado com detectores duplos, como se mostra na figura 7. A sua disposição geométrica está representada na figura.

Fig. 7 Diagrama geométrico do método do rolo modificado
Já em janeiro de 1977, Li Jiabao, do Instituto de Metais da Academia Chinesa de Ciências, propôs este método de ensaio e a fórmula de cálculo, como se mostra na Eq. (13) e na Eq. (14).
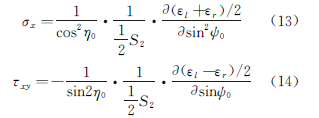
O método do rolo pode ser dividido em duas categorias: o método do ψ0 fixo e o método do ψ fixo.
O método ψ fixo é considerado superior ao método ψ0 fixo devido aos seus princípios mais exactos e resultados eficazes na prática.
Ao combinar estes dois métodos, o método do rolo fixo ψ, o fator de absorção pode ser igual a 1.
Isto significa que o pico de difração não se inclinará na parte inferior posterior, a forma do pico permanecerá simétrica e a forma e intensidade do pico permanecerão inalteradas, mesmo que o ângulo ψ mude, desde que não haja textura.
Esta caraterística aumenta consideravelmente a precisão da medição, tornando o método do rolo fixo ψ uma técnica de medição ideal.
O método de oscilação envolve a utilização de cada ângulo definido ψ (ou ângulo ψ0) como ponto central e a oscilação da ampola de raios X e do detetor para a esquerda e para a direita num ângulo específico (±Δψ ou ±Δψ0).
Este método aumenta o número de grãos que participam na difração, tornando-o um método eficaz para medir a tensão em materiais de grão grosseiro.
Podem também ser utilizados outros métodos de oscilação, como o método de oscilação do ângulo φ e o método de oscilação da translação X/Y, e podem mesmo ser combinados diferentes métodos de oscilação para efeitos de teste.
Em 2012, a PULSTEC, uma empresa sediada no Japão, introduziu um instrumento de stress que utiliza pela primeira vez a tecnologia de detetor bidimensional.
Este instrumento funciona utilizando um único modo de incidência e um detetor bidimensional para recolher informações de difração de raios X, permitindo-lhe recolher rapidamente dados do anel de Debye no ponto de ensaio.
Uma vez que o ângulo ψ formado pela normal à face do cristal e pela normal à superfície da amostra não se situa no mesmo plano para cada ponto do anel de Debye, o sin2O método ψ não pode ser utilizado para calcular a tensão. Em vez disso, é utilizado o método do ângulo α, ou cosα (como se mostra na Figura 8).
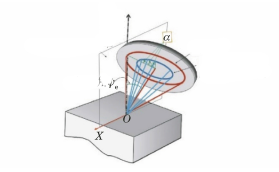
Fig. 8 Diagrama geométrico do método cosα
Este método de ensaio é ideal para medir a tensão superficial em grandes estruturas de aço.
No entanto, tem limitações quando se testam materiais de grão grosso ou materiais com textura.
O método cosα baseia-se nos princípios da elasticidade, como demonstrado pelas Equações (15) e (16).

A Figura 9 mostra a gama máxima de ângulos ψ que podem ser adquiridos utilizando um "detetor completo de duas posições" (com um ângulo de incidência de 45°).
O ângulo α encontra-se no plano do anel de Debye, que é o ângulo central de cada ponto do anel de Debye.

Fig. 9 Localização dos pontos de dados do método sin2ψ na curva s
Ambos os métodos de medição da tensão residual através da difração de raios X baseiam-se no mesmo princípio mecânico.
O tensor de deformação pode ser transformado no ângulo espacial, e o ângulo α utilizado no método cosα pode ser totalmente convertido para o ângulo ψ.
Na sua essência, o método cosα é essencialmente uma aproximação do método sin2Método ψ.
Normalmente, as chapas de aço laminadas a quente são consideradas isentas de textura. No entanto, algumas partes da chapa de aço podem apresentar textura devido a vários factores.
Apesar disto, muitos utilizadores ainda optam por utilizar a difração de raios X para medir a tensão residual nestes casos.
Por exemplo, se for selecionada uma chapa de aço laminada a quente com textura, as condições de ensaio e os resultados podem ser vistos no Quadro 1 e no Quadro 2. O relatório de ensaio para a medição da tensão residual no ponto Z (0) por cada instrumento é apresentado nas Figuras 10-13.
Quadro 1 Parâmetros de ensaio para a medição da tensão residual de materiais quentes Aço laminado Placa com diferentes instrumentos de tensão
| Tipo de equipamento | μ-X360S | PROTO LXRD | X-RAYBOT | XL-640 |
| método de ensaio | cosα | pecado2ψ | pecado2ψ | pecado2ψ |
| Tensão/kV | 20 | 30 | 20 | 25 |
| Corrente/mA | 1 | 25 | 1 | 6 |
| Ponto iluminado/mm | 1 | 1 | 1 | 1 |
| ψ Gama/(°) | – | -35~35 | -40~40 | 0~45 |
| Método de cálculo da deformação | – | Método do valor D | Método de deformação | Método de deformação |
| Método de determinação do pico | – | PessoaVII | Ponto médio | Método de correlação cruzada |
| Tensão residual/MPa | 78 | 213.6 | 144 | 113 |
Quadro 2 Tensões residuais de chapas de aço laminadas a quente medidas por diferentes instrumentos de medição de tensões
| Ponto de controlo | μ-X360S | PROTO LXRD | X-RAYBOT | XL-640 |
| Z(5) | 29,47 | 122 | 107 | 77 |
| Z(4) | 37,52 | 135 | 112 | 70 |
| Z(3) | 74,70 | 104 | 95 | 67 |
| Z(2) | 38,28 | 153 | 99 | 134 |
| Z(1) | 37,64 | 166 | 122 | 101 |
| Z(0) | 64,78 | 144 | 213 | 113 |
| Z(-1) | 72,71 | 138 | 97 | 139 |
| Z(-2) | 62,52 | 134 | 83 | 145 |
| Z(-3) | 75,70 | 120 | 93 | 153 |
| Z(-4) | 63,56 | 114 | 80 | 148 |
| Z(-5) | 79,27 | 94 | 93 | 152 |

Fig. 10 Anel de Debye no ponto Z (0) medido com um medidor de tensões do tipo μ-X360S

Fig. 11 2θ-sin2Curva ψ de Z (0) medida pelo medidor de tensão PROTO LXRD

Fig. 12 2θ-sin2Curva ψ do ponto de medição Z (0) com o medidor de tensão X-RAYBOT

Fig. 13 ε-sin2Curva ψ de Z (0) medida com o medidor de tensão XL-640
A tensão residual medida pelo método c é menor do que a medida pelo método s.
Para o ponto de ensaio Z (0), é utilizado o medidor de tensão. De acordo com o princípio do espaçamento igual de sin2ψ, são seleccionados 8 ângulos ψ dentro do intervalo de 0 °~45 °.
Os resultados são apresentados nas Fig. 14-15. Verifica-se que o sin2A curva ψ do material apresenta um tipo de "choque" devido à textura.
A ordenada do pecado2A curva ψ na Fig. 13 é a deformação ε. Depois de alterar a ordenada para 2θ, efetuar o ajuste linear. Os resultados são apresentados na Fig. 14.
O declive M da linha de ajuste é -0,355, e a tensão residual σ é 113MPa.

Fig. 14 Resultados do ajustamento de 2θ-sin2Curva ψ medida pelo medidor de tensão XL-640 no ponto Z (0)
O intervalo ψ selecionado pelo medidor de tensão μ-X360S é equivalente aos dois primeiros valores 2θ da blindagem e, em seguida, é efectuado o ajuste da linha reta. Os resultados são apresentados na Fig. 15.

Fig. 15 Resultados do ajuste de 2θ-sin2Curva ψ de Z (0) medida por um instrumento de tensão do tipo μ-X360S
Utilizar o medidor de tensão PROTO LXRD para testar o intervalo ψ selecionado, proteger os últimos três valores 2θ na Fig. 14 e, em seguida, efetuar o ajuste linear. Os resultados são apresentados na Fig.16.

Fig. 16 Resultados do ajustamento de 2θ-sin2Curva ψ medida pelo medidor de tensão PROTO LXRD no ponto Z (0)
Pode ver-se na Figura 12 que o valor máximo de sin2O valor ψ do ponto Z (0) é 0,4 utilizando o medidor de tensão X-RAYBOT.
De acordo com o intervalo ψ selecionado, proteja os dois últimos valores 2θ na Fig. 14 e, em seguida, efectue o ajuste linear. Os resultados são apresentados na Fig. 17.

Fig. 17 Resultados do ajuste de 2θ-sin2Curva ψ de Z (0) medida pelo verificador de tensões X-RAYBOT
Devido à textura do material, a sua sin2A curva ψ é oscilatória.
A gama de ângulos ψ selecionada é diferente, o que resulta em diferenças no declive e nos valores de tensão residual obtidos a partir da linha de ajuste.
Para materiais com textura desconhecida e grão grosseiro, não é aconselhável escolher um intervalo ψ estreito e um pequeno número de estações ψ para a medição da tensão residual, uma vez que isso pode levar a erros de medição significativos.
O encaixe linear pode não ser adequado para materiais com pele texturizada2curvas ψ que são oscilatórias.
Durante o processo de medição, o ajuste linear é frequentemente utilizado para mitigar as flutuações causadas por vibrações e erros de medição.
Pode não ser viável atingir um ângulo ψ de 45°, uma vez que este poderia ser influenciado pela profundidade de penetração. É mais provável que um ângulo maior produza resultados mais exactos, desde que a profundidade de penetração possa ser ignorada.
Para materiais com grão ou textura grosseiros, a gama de ângulos ψ deve ser alargada tanto quanto possível para eliminar os efeitos de ε-sin2distribuição ψ. Isto pode ser conseguido medindo ambos os ângulos ±ψ.
A precisão das linhas rectas ajustadas pode ser melhorada utilizando o método dos mínimos quadrados para ajustar a regressão e aumentando tanto o intervalo ψ como o número de estações ψ. Isto resultará em valores de teste mais fiáveis.
A precisão da medição pode também ser melhorada aumentando a área de exposição aos raios X ou aumentando o número de grãos de difração que participam no método de oscilação.
(1) O pecado2O método ψ pode ser utilizado para determinar a tensão residual com maior precisão, aumentando o intervalo de ψ e seleccionando mais estações ψ. No entanto, este método tem limitações, uma vez que envolve uma única exposição, o que pode resultar em grandes erros de medição se o intervalo de ψ não for suficiente.
(2) Nos métodos de medição que utilizam o sin2ψ princípio, o método do rolo é superior ao método da inclinação. Recomenda-se a utilização do método do rolo sempre que as condições de espaço no ponto de medição o permitam. Para medir a tensão residual em ranhuras de certos componentes, o método de co-inclinação é normalmente utilizado.
(3) O método da deformação real é o método preferido para calcular a tensão residual.
(4) O método sin2ψ é considerado um método padrão para este fim. Para obter os resultados mais exactos, o ângulo ψ deve ser definido utilizando o método sin2Método da bissecção de valor ψ e deve ser medido o maior número possível de ângulos ψ.