Você já se perguntou como calcular com precisão a tolerância de dobra para seus projetos de fabricação de metal? Nesta postagem do blog, exploraremos o fascinante mundo das fórmulas e cálculos de tolerância à flexão. Como engenheiro mecânico experiente, eu o guiarei pelos principais conceitos e fornecerei insights práticos para ajudá-lo a dominar esse aspecto crucial do projeto de chapas metálicas. Prepare-se para mergulhar de cabeça e desvendar os segredos da criação de dobras precisas e eficientes em seus projetos!
A tolerância de dobra é um conceito crítico no campo da fabricação de chapas metálicas, principalmente quando se trabalha com operações de dobra. Ele se refere ao comprimento adicional de material necessário para acomodar a dobra na chapa metálica. Compreender e calcular com precisão a tolerância de dobra é essencial para garantir que as dimensões finais da peça dobrada atendam às especificações do projeto.
Cálculos precisos de tolerância de dobra são vitais no processo de fabricação. Quando uma folha plana de metal é dobrada, o material na parte externa da dobra se estica, enquanto o material na parte interna se comprime. Sem levar em conta essa deformação, o produto final não corresponderia ao projeto pretendido, levando a imprecisões e possíveis falhas. A tolerância de dobra ajuda os fabricantes a ajustar as dimensões do padrão plano, garantindo que a peça dobrada atenda a requisitos precisos.
Vários parâmetros críticos influenciam os cálculos de tolerância de dobra:
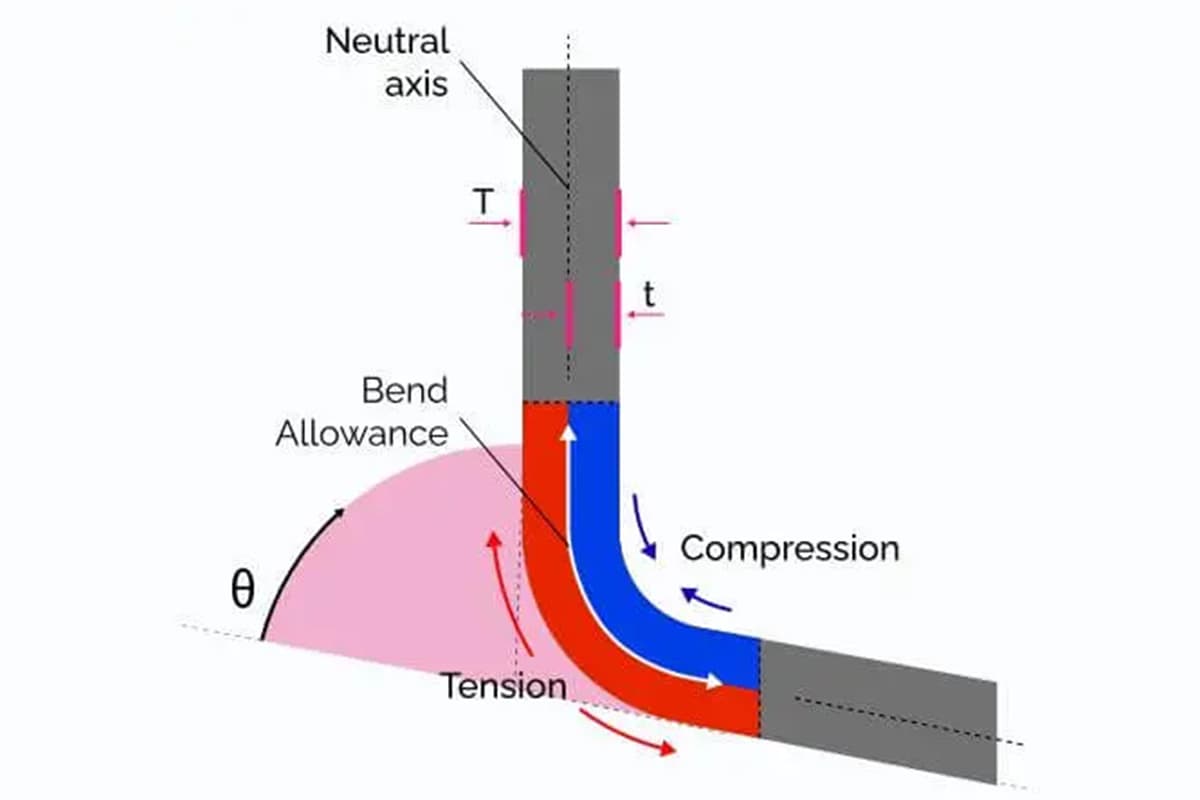
O conceito de subsídio de flexão é o seguinte: quando uma folha de metal é dobrada, ela tem três dimensões - duas dimensões externas (L1 e L2) e uma dimensão de espessura (T).
É importante observar que a soma de L1 e L2 é maior do que o comprimento desdobrado (L), e a diferença entre os dois é conhecida como tolerância de flexão (K).
Portanto, o comprimento desdobrado de uma curva pode ser calculado como L = L1 + L2 - K.
Leitura relacionada:
Como foi a fórmula para tolerância a dobras criado? E como você calcula tolerância a dobras?
A tolerância de dobra depende do raio interno formado. A abertura inferior da matriz em V determina o raio interno (I.R.) de uma peça formada. O raio interno do aço doce é 5/32 x abertura inferior da matriz em V (W) quando o raio do punção é menor que 5/32 x W.
Se I.R.< Espessura do material (t)
Se I.R.> 2 x Espessura do material (t)
Onde A= (180 - ângulo de inclusão da dobra)
Se o raio interno for igual a t ou 2t, ou entre t e 2t, a tolerância de dobra é calculada interpolando os valores de tolerância de dobra das duas fórmulas mencionadas acima.
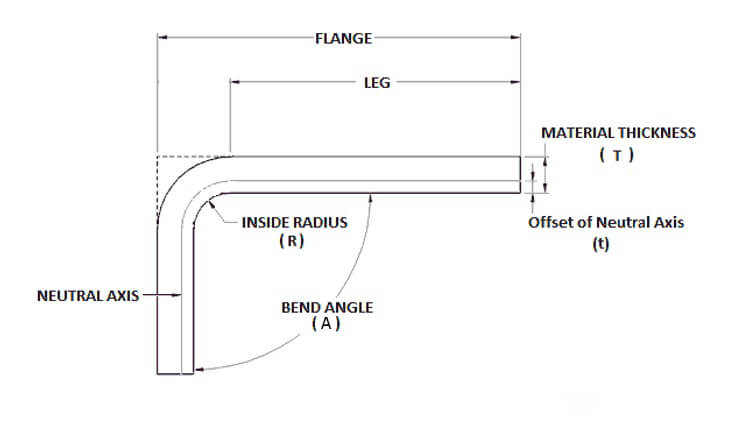
Além disso, para calcular essa tolerância à flexão, você também pode usar a seguinte fórmula:
Essa fórmula considera as diversas geometrias e propriedades das peças a serem formadas.
A espessura do material (T), o ângulo de curvatura (A), a raio de curvatura (R) e o fator K do material a ser dobrado são os fatores mais importantes nesse cálculo.
Como fica evidente na fórmula acima, o cálculo da tolerância à flexão é um processo simples.
Você pode determinar a tolerância à flexão substituindo os valores mencionados acima na fórmula.
Quando o ângulo de flexão é de 90°, a fórmula da tolerância de flexão pode ser simplificada da seguinte forma:
Observação: O fator K para a maioria dos materiais e espessuras padrão geralmente fica entre 0 e 0,5.
Você pode calcular com precisão o valor do fator K usando o seguinte Calculadora do fator K:
A fórmula de tolerância de dobra (BA) é essencial para calcular o comprimento do material necessário para formar uma dobra. Essa fórmula geral é amplamente aplicável em diferentes materiais e métodos de dobra:
Onde:
O fator K é fundamental, pois indica a posição do eixo neutro, que não muda de comprimento durante a flexão. Normalmente, o fator K varia entre 0,3 e 0,5 e depende do tipo de material, da espessura, do raio e do método de flexão.
Materiais diferentes têm propriedades exclusivas que exigem ajustes nos cálculos de tolerância de dobra. Esses ajustes garantem a precisão, especialmente em curvas de 90°:
Para materiais mais macios, como latão macio ou cobre, a tolerância de dobra é calculada da seguinte forma:
BA = (0,55 × T) + (1,57 × R
Esse ajuste leva em conta a ductilidade do material e a menor resistência à deformação.
Para cobre ou latão semiduro, aço macio e alumínio, a tolerância de dobra é:
BA = (0,64 x T) + (1,57 × R)
Esses materiais têm dureza moderada, exigindo uma tolerância um pouco maior do que os materiais mais macios.
Para materiais mais duros, como bronze, cobre duro, aço laminado a frio e aço para molas, a fórmula é:
BA = (0,71 x T) + (1,57 × R)
Esses materiais são mais resistentes à flexão, o que exige uma tolerância maior.
Para determinar o comprimento plano total da peça de chapa metálica, a tolerância de dobra é adicionada aos comprimentos das partes planas:
Comprimento plano = Comprimento da perna 1 + BA + Comprimento da perna 2
Essa abordagem garante que as dimensões finais da peça sejam precisas após a dobra.
Considere uma dobra de 90° em uma folha de alumínio com espessura de 2 mm e um raio de dobra interno de 5 mm. Usando a fórmula específica do material para cobre semiduro, latão, aço macio e alumínio:
BA = (0,64 × 2) + (1,57 × 5)
BA = 1,28 + 7,85=9,13
Se a peça tiver duas seções planas de 50 mm cada, o comprimento plano total será:
Comprimento plano = 50 + 9,13 + 50 = 109,13 mm
Além da tolerância de curvatura, a dedução de curvatura (BD) e o recuo externo (OSSB) são importantes para medições precisas:
Dedução de dobra (BD) = OSSB - BA
Onde:
Essas formulações e considerações são essenciais para calcular com precisão as tolerâncias de dobra, garantindo que as peças de chapa metálica sejam fabricadas com as dimensões e o ajuste corretos.
A tolerância de dobra é um fator crítico no processo de dobra de chapas metálicas, especialmente para materiais como o alumínio. Ela é responsável pelo estiramento do material que ocorre durante a dobra, garantindo dimensões finais precisas. Aqui, discutiremos a fórmula específica usada para chapas de alumínio e sua aplicação.
A tolerância de flexão para uma placa de alumínio pode ser calculada usando a seguinte fórmula:
𝐿=𝐿1+𝐿2-1.6𝑇
Onde:
O valor 1,6𝑇 é derivado empiricamente, o que significa que foi estabelecido por meio de experimentos práticos e experiência de produção. Esse fator leva em conta o comportamento do material durante a flexão, garantindo que as dimensões finais sejam precisas.
É fundamental observar que essa fórmula é aplicável especificamente sob determinadas condições:
Para determinar o tamanho expandido da placa de alumínio, siga estas etapas:
Esse cálculo lhe dará o comprimento do padrão plano necessário antes da dobra, garantindo que a peça dobrada final tenha as dimensões corretas.
A calculadora de tolerância de dobra fornecida abaixo simplifica o processo de cálculo do valor da tolerância de dobra, que é crucial para a fabricação precisa de chapas metálicas. A tolerância de dobra é o comprimento do eixo neutro entre as linhas de dobra, o que ajuda a determinar o tamanho correto do blank para uma peça dobrada.
O ângulo de dobra, denotado como θ, é um parâmetro crucial na fórmula de tolerância de dobra. Ele representa o ângulo pelo qual a chapa metálica é dobrada. Normalmente, o ângulo de dobra é medido em graus, mas pode ser convertido em radianos por meio da fórmula:
O raio interno, representado como r, é o raio da curva interna da dobra. Esse raio influencia diretamente a quantidade de alongamento e compressão que ocorre dentro do material durante a dobra. Um raio interno menor resulta em uma deformação mais significativa, que deve ser considerada no cálculo da tolerância de dobra.
A espessura do material, indicada como T, é a espessura da chapa metálica que está sendo dobrada. Materiais mais espessos sofrem alongamento e compressão mais pronunciados, afetando a tolerância geral de dobra. A medição precisa da espessura do material é essencial para cálculos precisos da tolerância de dobra.
O fator K é um valor sem dimensão que representa a posição do eixo neutro em relação à espessura do material. O eixo neutro é a linha teórica dentro do material que permanece inalterada em comprimento durante a flexão. O fator K varia de acordo com as propriedades do material e os métodos de flexão, normalmente entre 0,3 e 0,5 para a maioria dos materiais. A fórmula para a posição do eixo neutro é:
Posição do eixo neutro = K × T
O eixo neutro é a linha imaginária dentro do material que permanece inalterada em seu comprimento durante a dobra. Compreender sua posição é fundamental para calcular a tolerância de dobra correta.
A tolerância de dobra, representada como BA, é o comprimento do eixo neutro necessário para formar uma dobra. Ele é calculado por meio da fórmula:
Essa fórmula usa o ângulo de curvatura, o raio interno, a espessura do material e o fator K para garantir cálculos precisos de tolerância de curvatura.
A tabela de tolerância de dobra é um recurso essencial para profissionais que trabalham com fabricação de chapas metálicas. Ela fornece uma listagem abrangente dos principais parâmetros, como espessura do material, raio de curvatura, ângulo de curvatura, tolerância de curvatura e valores de dedução de curvatura para materiais comuns. Essas informações são cruciais para calcular com precisão o comprimento de desenvolvimento de uma peça de chapa metálica após a dobra.
Leia mais:
| TV | Ângulo | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Tamanho mais curto |
| V4 | 90 | 0.9 | 1.4 | 2.8 | ||||||||||
| V4 | 120 | 0.7 | ||||||||||||
| V4 | 150 | 0.2 | ||||||||||||
| V6 | 90 | 1.5 | 1.7 | 2.15 | 4.5 | |||||||||
| V6 | 120 | 0.7 | 0.86 | 1 | ||||||||||
| V6 | 150 | 0.2 | 0.3 | 0.4 | ||||||||||
| V7 | 90 | 1.6 | 1.8 | 2.1 | 2.4 | 5 | ||||||||
| V7 | 120 | 0.8 | 0.9 | 1 | ||||||||||
| V7 | 150 | 0.3 | 0.3 | 0.3 | ||||||||||
| V8 | 90 | 1.6 | 1.9 | 2.2 | 2.5 | 5.5 | ||||||||
| V8 | 30 | 0.3 | 0.34 | 0.4 | 0.5 | |||||||||
| V8 | 45 | 0.6 | 0.7 | 0.8 | 1 | |||||||||
| V8 | 60 | 1 | 1.1 | 1.3 | 1.5 | |||||||||
| V8 | 120 | 0.8 | 0.9 | 1.1 | 1.3 | |||||||||
| V8 | 150 | 0.3 | 0.3 | 0.2 | 0.5 | |||||||||
| V10 | 90 | 2.7 | 3.2 | 7 | ||||||||||
| V10 | 120 | 1.3 | 1.6 | |||||||||||
| V10 | 150 | 0.5 | 0.5 | |||||||||||
| V12 | 90 | 2.8 | 3.65 | 4.5 | 8.5 | |||||||||
| V12 | 30 | 0.5 | 0.6 | 0.7 | ||||||||||
| V12 | 45 | 1 | 1.3 | 1.5 | ||||||||||
| V12 | 60 | 1.7 | 2 | 2.4 | ||||||||||
| V12 | 120 | 1.4 | 1.7 | 2 | ||||||||||
| V12 | 150 | 0.5 | 0.6 | 0.7 | ||||||||||
| V14 | 90 | 4.3 | 10 | |||||||||||
| V14 | 120 | 2.1 | ||||||||||||
| V14 | 150 | 0.7 | ||||||||||||
| V16 | 90 | 4.5 | 5 | 11 | ||||||||||
| V16 | 120 | 2.2 | ||||||||||||
| V16 | 150 | 0.8 | ||||||||||||
| V18 | 90 | 4.6 | 13 | |||||||||||
| V18 | 120 | 2.3 | ||||||||||||
| V18 | 150 | 0.8 | ||||||||||||
| V20 | 90 | 4.8 | 5.1 | 6.6 | 14 | |||||||||
| V20 | 120 | 2.3 | 3.3 | |||||||||||
| V20 | 150 | 0.8 | 1.1 | |||||||||||
| V25 | 90 | 5.7 | 6.4 | 7 | 17.5 | |||||||||
| V25 | 120 | 2.8 | 3.1 | 3.4 | ||||||||||
| V25 | 150 | 1 | 1 | 1.2 | ||||||||||
| V32 | 90 | 7.5 | 8.2 | 22 | ||||||||||
| V32 | 120 | 4 | ||||||||||||
| V32 | 150 | 1.4 | ||||||||||||
| V40 | 90 | 8.7 | 9.4 | 28 | ||||||||||
| V40 | 120 | 4.3 | 4.6 | |||||||||||
| V40 | 150 | 1.5 | 1.6 |
| TV | Ângulo | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Tamanho mais curto |
| V4 | 1.4 | 2.8 | ||||||||||||
| V6 | 1.6 | 4.5 | ||||||||||||
| V7 | 1.6 | 1.8 | 5 | |||||||||||
| V8 | 1.8 | 2.4 | 3.1 | 5.5 | ||||||||||
| V10 | 2.4 | 3.2 | 7 | |||||||||||
| V12 | 2.4 | 3.2 | 8.5 | |||||||||||
| V14 | 3.2 | 10 | ||||||||||||
| V16 | 3.2 | 4 | 4.8 | 11 | ||||||||||
| V18 | 4.8 | 13 | ||||||||||||
| V20 | 4.8 | 14 | ||||||||||||
| V25 | 4.8 | 5.4 | 6 | 17.5 | ||||||||||
| V32 | 6.3 | 6.9 | 22 |
| Ângulo | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Tamanho mais curto |
| 90 | 3.6 | 5.2 | 6.8 | 8.4 | 28 | ||||||||
| 120 | |||||||||||||
| 150 |
| MATERIAL | SPCC | SUS | Al （LY12） | CCEE | ||||
|---|---|---|---|---|---|---|---|---|
| T | ΔT | ΔK | ΔT | ΔK | ΔT | ΔK | ΔT | ΔK |
| T=0.6 | 1.25 | 1.26 | ||||||
| T=0.8 | 0.18 | 1.42 | 0.15 | 1.45 | 0.09 | 1.51 | ||
| T=1.0 | 0.25 | 1.75 | 0.20 | 1.80 | 0.30 | 1.70 | 0.38 | 1.62 |
| T=1.2 | 0.45 | 1.95 | 0.25 | 2.15 | 0.50 | 1.90 | 0.43 | 1.97 |
| T=1.4 | 0.64 | 2.16 | ||||||
| T=1.5 | 0.64 | 2.36 | 0.50 | 2.50 | 0.70 | 2.30 | ||
| T=1.6 | 0.69 | 2.51 | ||||||
| T=1.8 | 0.65 | 3.00 | ||||||
| T=1.9 | 0.60 | 3.20 | ||||||
| T=2.0 | 0.65 | 3.35 | 0.50 | 3.50 | 0.97 | 3.03 | 0.81 | 3.19 |
| T=2.5 | 0.80 | 4.20 | 0.85 | 4.15 | 1.38 | 3.62 | ||
| T=3.0 | 1.00 | 5.00 | 5.20 | 1.40 | 4.60 | |||
| T=3.2 | 1.29 | 5.11 | ||||||
| T=4.0 | 1.20 | 6.80 | 1.00 | 7.00 | ||||
| T=5.0 | 2.20 | 7.80 | 2.20 | 7.80 | ||||
| T=6.0 | 2.20 | 9.80 | ||||||
Observação:
Uma tabela de tolerância de dobra bem mantida é uma ferramenta vital no setor de fabricação de chapas metálicas. Ela garante precisão e eficiência no processo de dobra, levando a produtos acabados de maior qualidade e mais precisos. Ao compreender e utilizar os valores fornecidos na tabela, os engenheiros e fabricantes podem obter os melhores resultados em seus projetos.
Na fabricação de chapas metálicas, obter precisão e exatidão é fundamental para criar peças de alta qualidade. Um dos principais fatores que desempenham um papel significativo nesse processo é o fator K. Compreender o fator K e sua aplicação nos cálculos de tolerância de dobra é essencial para que os fabricantes produzam peças que atendam às especificações exatas e tenham um desempenho confiável em vários setores.
O fator K é um valor sem dimensão que representa a relação entre a distância do eixo neutro e a espessura do material. Ele é crucial para cálculos precisos de tolerância de dobra, que determinam a quantidade de material necessária para obter uma dobra desejada. O eixo neutro é uma linha imaginária dentro do material que não muda de comprimento durante a flexão. Ao compreender o fator K, os fabricantes podem prever como o material se comportará quando dobrado, garantindo processos de fabricação precisos e eficientes.
O fator K é calculado usando a fórmula:
Onde:
O uso do fator K na fórmula de tolerância à flexão ajuda a prever o alongamento e a compressão do material durante a flexão. A fórmula da tolerância de dobra é:
Para ilustrar isso, vamos ver um exemplo simples. Suponha que tenhamos uma peça de chapa metálica com espessura (T) de 2 mm, dobrada em um ângulo de 90 graus (θ), com um raio interno (r) de 5 mm e um fator K (K) de 0,4.
1. Converta o ângulo de curvatura em radianos:
2. Aplique os valores à fórmula de tolerância de dobra:
Esse cálculo mostra que são necessários aproximadamente 9,11 mm de material ao longo do eixo neutro para obter a curvatura desejada, demonstrando a importância de um fator K preciso.
O fator K afeta diretamente a precisão dos cálculos de tolerância de dobra. Um fator K preciso garante que as dimensões finais da peça dobrada correspondam às especificações do projeto, reduzindo o desperdício de material e a necessidade de retrabalho. Essa precisão é vital para os setores em que as dimensões exatas são cruciais para a montagem e a funcionalidade dos componentes.
Diferentes materiais têm propriedades mecânicas exclusivas, o que resulta em valores variáveis de fator K. Materiais mais macios, como o alumínio, normalmente têm um fator K menor, enquanto materiais mais duros, como o aço inoxidável, têm um fator K maior. A compreensão dessas variações permite que os fabricantes selecionem valores de fator K apropriados para diferentes materiais, garantindo cálculos precisos e processos de fabricação eficientes.
Veja abaixo as respostas para algumas perguntas frequentes:
A fórmula de tolerância de dobra é usada para calcular o comprimento do eixo neutro de uma dobra em chapa metálica, o que é crucial para determinar o comprimento correto do padrão plano antes de o metal ser dobrado. Esse cálculo garante que as dimensões finais da peça dobrada correspondam às especificações do projeto.
A fórmula leva em conta vários parâmetros importantes:
A fórmula geral para a tolerância de curvatura (BA) é:
Usando essa fórmula, você pode calcular o comprimento exato do material necessário para formar uma dobra, garantindo que o material não se estique excessivamente nem se comprima demais. Essa margem de dobra calculada é então adicionada aos comprimentos das pernas da peça para desenvolver um padrão plano preciso, o que é essencial para a produção de peças com dimensões precisas.
A fórmula de tolerância de dobra também está relacionada à dedução de dobra, que é o comprimento que precisa ser subtraído do comprimento total da chapa metálica para obter o padrão plano correto. A dedução de dobra é calculada usando a tolerância de dobra e o recuo externo, garantindo que as dimensões finais da peça sejam precisas após a dobra.
Por exemplo, se você estiver dobrando uma chapa de aço inoxidável de 2 mm de espessura em um ângulo de 90° com um raio de curvatura interno de 3 mm e um fator K de 0,44, a tolerância de curvatura poderá ser calculada da seguinte forma:
Essa tolerância de dobra é então usada para garantir que o padrão plano seja desenvolvido corretamente, resultando em uma peça que atenda às especificações do projeto. Em resumo, a fórmula de tolerância de dobra é essencial para a fabricação precisa de chapas metálicas, garantindo que as peças finais sejam produzidas com as dimensões corretas.
Para calcular a tolerância de dobra em chapas metálicas, é necessário determinar vários parâmetros-chave: espessura do material (T), ângulo de dobra (θ), raio interno (r) e o fator K (K). A tolerância de dobra (BA) é calculada por meio da fórmula:
Aqui está um processo passo a passo:
Usando essa fórmula, para os mesmos parâmetros:
Seguindo essas etapas e usando a fórmula apropriada, você pode calcular com precisão a tolerância de dobra para suas peças de chapa metálica, garantindo uma fabricação precisa.
O fator K é importante na fórmula de tolerância de dobra por vários motivos, cada um deles destacando sua importância na fabricação de chapas metálicas de precisão. Em primeiro lugar, ele representa a relação entre o eixo neutro e a espessura do material. Durante a dobra, o eixo neutro se desloca de sua localização original em 50% da espessura do material em direção à superfície interna da dobra. Esse deslocamento é fundamental porque determina a quantidade de alongamento que ocorre no material. O fator K ajuda a calcular esse novo local, o que é essencial para cálculos precisos de dobra.
Em segundo lugar, o fator K é fundamental para calcular a tolerância de dobra, que é o comprimento da fibra neutra do início ao fim do arco gerado pela dobra. Esse cálculo é necessário para determinar o tamanho plano da chapa metálica necessária para obter a forma de dobra desejada. A margem de curvatura é diretamente influenciada pelo fator K, pois ele considera o alongamento do material durante o processo de curvatura.
Além disso, o uso do fator K permite cálculos precisos de deduções de dobras, recuos externos e o layout plano geral da peça. Essa precisão é vital, pois garante que as dimensões finais da peça dobrada correspondam às especificações do projeto, evitando erros que poderiam surgir do uso de valores genéricos ou imprecisos do fator K.
O fator K varia com base em vários parâmetros, incluindo o tipo de material, a espessura, o método de formação, as ferramentas e o ângulo de dobra. Essa variabilidade significa que o fator K deve ser adaptado às condições específicas do processo de dobra. Ao considerar esses fatores, o fator K ajuda a personalizar a fórmula de compensação de dobra para obter resultados mais precisos.
Por fim, um valor correto do fator K é essencial para evitar erros nas dimensões finais da chapa dobrada. Valores incorretos do fator K podem levar a imprecisões nas tolerâncias de dobra, resultando em peças que não atendem às especificações exigidas. Portanto, determinar e usar com precisão o fator K é fundamental para a produção de componentes de alta qualidade.
Em resumo, o fator K é importante porque permite o cálculo preciso das tolerâncias de dobra, leva em conta o deslocamento do eixo neutro e considera os parâmetros específicos do material e do processo, todos essenciais para obter resultados precisos e confiáveis na dobra de chapas metálicas.
A fórmula de tolerância de dobra na dobra de chapas metálicas geralmente inclui diversas variáveis importantes:
A tolerância de curvatura (BA) pode ser calculada usando a fórmula:
ou
em que (0,017453) é (π/180) e (0,0078) é (π /180) x K) - fator.
Essas variáveis são essenciais para determinar com precisão a tolerância de dobra, o que é fundamental para a fabricação precisa de chapas metálicas.
Sim, a fórmula de tolerância de dobra pode variar significativamente com base no tipo de material, bem como em outros fatores, como a espessura do material, o ângulo de dobra e o processo de dobra específico.
O fator K, um componente essencial da fórmula de tolerância à flexão, representa o deslocamento do eixo neutro teórico durante a flexão e varia de acordo com o material. Por exemplo, o aço macio laminado a frio normalmente usa um fator K em torno de 0,446, enquanto outros materiais, como aço inoxidável e alumínio, têm fatores K diferentes devido às suas propriedades e comportamentos de flexão exclusivos.
A fórmula de tolerância de dobra também incorpora a espessura do material e o ângulo de dobra, que podem diferir entre os materiais. Uma forma geral da fórmula de tolerância de dobra é:
onde:
Diferentes materiais têm propriedades distintas, como elasticidade, resistência à tração e direção do grão, que influenciam seu comportamento de flexão. Por exemplo, o alumínio se dobra mais facilmente do que o aço, exigindo ajustes no cálculo da tolerância de dobra. Além disso, dobrar um metal ao longo de sua direção de grão pode exigir mais força e uma tolerância de dobra diferente em comparação com a dobra ao longo do grão.
A tendência do material de se recuperar após a flexão, conhecida como retorno elástico, também deve ser considerada. Isso envolve dobrar ligeiramente o material para levar em conta a recuperação elástica, influenciada pelo tipo de material e suas propriedades.
Em resumo, a fórmula da tolerância de dobra deve ser adaptada ao material específico que está sendo usado, considerando suas propriedades exclusivas, sua espessura e o processo de dobra envolvido.
Como fundador do MachineMFG, dediquei mais de uma década de minha carreira ao setor de metalurgia. Minha vasta experiência permitiu que eu me tornasse um especialista nas áreas de fabricação de chapas metálicas, usinagem, engenharia mecânica e máquinas-ferramentas para metais. Estou sempre pensando, lendo e escrevendo sobre esses assuntos, esforçando-me constantemente para permanecer na vanguarda do meu campo. Permita que meu conhecimento e experiência sejam um trunfo para sua empresa.
PT_BR 
EN 
AR 
DE 
ES 
FR 
ID 
IT 
JA 
NL 
PT 
RU 
KO 
TR