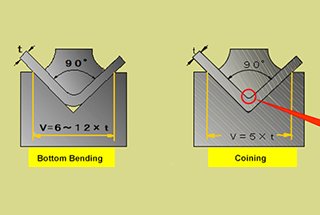
Você já se perguntou como as chapas metálicas são transformadas em formas complexas? A dedução de dobras, um conceito crucial na fabricação de chapas metálicas, é a chave. Nesta postagem do blog, vamos nos aprofundar nos meandros da dedução de dobras, explorando suas fórmulas, calculadoras e aplicações práticas. Junte-se a nós para desvendar os segredos por trás da criação de componentes de chapa metálica precisos e bonitos.


Calculadoras relacionadas:
A dedução de dobra é um conceito crucial no campo da fabricação de chapas metálicas, especialmente no processo de dobra. Ela é comumente chamada de "quantidade de recuo" e desempenha um papel significativo na determinação das dimensões precisas de uma peça dobrada.
A dedução de dobra (BD) é o valor subtraído do comprimento total da chapa metálica plana para atingir as dimensões finais desejadas após a dobra. Ela é responsável pelo material que é deslocado durante o processo de dobra.
Importância na dobragem de chapas metálicas
A dedução de dobra é essencial para calcular com precisão o padrão plano de uma peça de chapa metálica antes de ser dobrada. Ela garante que as dimensões finais da peça dobrada correspondam às especificações do projeto. Sem levar em conta a dedução de dobra, a peça pode acabar com dimensões incorretas, levando a possíveis problemas de montagem e funcionalidade.
Vários fatores podem influenciar o valor da dedução de dobra, inclusive:
Na prática, a dedução de dobra é determinada por meio de dados empíricos, diretrizes do fabricante ou software especializado que leva em conta as propriedades específicas do material e o processo de dobra. Cálculos precisos de dedução de dobra são essenciais para garantir que o produto final atenda aos requisitos do projeto e funcione corretamente na aplicação pretendida.
A dedução de dobra (BD) é um fator crítico na fabricação de chapas metálicas, usado para calcular o comprimento do padrão plano de uma peça de chapa metálica. Ele considera o material que é deslocado durante o processo de dobra. Esse valor é essencial para garantir que as dimensões finais da peça dobrada sejam precisas.
A fórmula de dedução de dobra é usada para determinar o comprimento plano de uma peça de chapa metálica antes de ser dobrada. A fórmula é a seguinte:
Lt=A+B-BD
Onde:
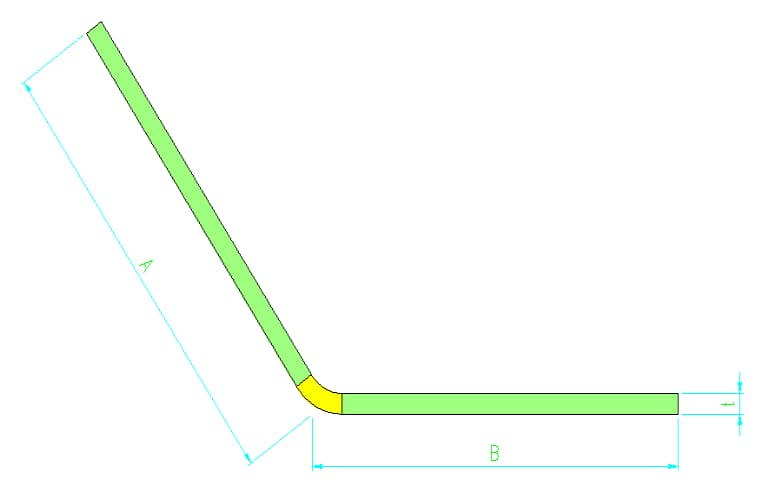
A dedução de dobra no Solidworks é usada somente para o cálculo de dobras de 90 graus em chapas metálicas.
No entanto, ele também pode ser usado para o cálculo de desdobramento de chapas metálicas sem 90 graus, mas o valor de dedução de dobra para dobra sem 90 graus precisa ser usado de acordo com a tabela de coeficiente de dobra.
Cada fabricante tem uma tabela diferente, e pode haver erros. Algumas fábricas de chapas metálicas podem não usar frequentemente dobras que não sejam de 90 graus.
Hoje, compartilharei o método de cálculo para a dedução de flexão de 90 graus que conheço.
A dedução de dobra é um fator crucial na fabricação de chapas metálicas, principalmente quando se usam máquinas como freios de prensa. Ela representa a quantidade de material consumido durante o processo de dobra. O cálculo preciso das deduções de dobra é essencial para obter dimensões precisas da peça e uso eficiente do material. Este artigo discute três métodos comuns para calcular as deduções de dobra.
O método mais simples usa um fator de multiplicação baseado na espessura do material:
Esse método é rápido e fácil, mas carece de precisão. É adequado para aplicações com requisitos de precisão menores ou para estimativas iniciais.
Uma abordagem mais refinada desenvolvida pelo setor de chapas metálicas:
Dedução de flexão = 2 × espessura do material + 1/3 × espessura do material
Essa fórmula leva em conta o alongamento do material durante a flexão. Ela é derivada de: Comprimento não dobrado = Comprimento A + Comprimento B - Dedução de flexão
Quando a dedução de flexão considera tanto a espessura quanto o alongamento do material.
Uma fórmula mais sofisticada derivada de estudos empíricos:
Dedução de flexão = 2 × t - (0,72t - 0,075V - 0,01)
Onde:
Essa fórmula leva em conta a influência da largura inferior da matriz na dedução da dobra. Ela é particularmente precisa para chapas de aço-carbono, mas tem mostrado bons resultados com outros materiais, como o alumínio, quando a largura da matriz é cerca de 4 vezes a espessura do material.
Considerações importantes
Conclusão
A escolha do método adequado de cálculo da dedução de dobra depende da precisão necessária, do tipo de material e das informações disponíveis sobre as ferramentas. Para trabalhos de alta precisão, recomenda-se a fórmula avançada (Método 3), enquanto os métodos mais simples podem ser úteis para estimativas rápidas ou aplicações menos críticas.
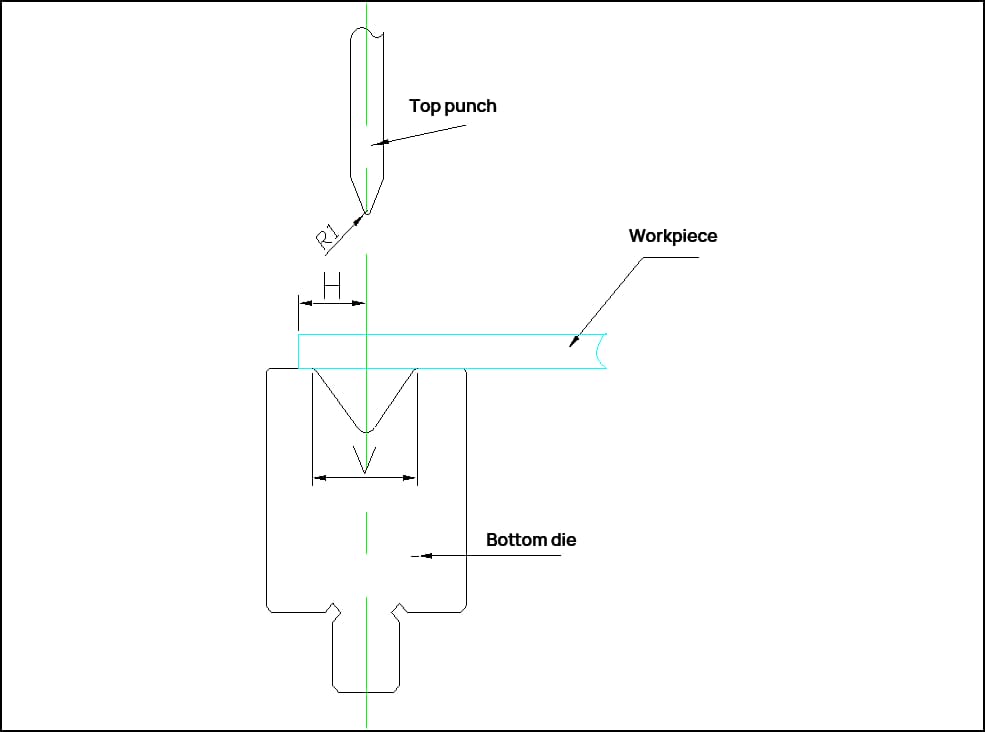
| V | Largura da matriz w | Raio de curvatura | T | 30° | 45° | 60° | 90° | 120° | 150° | 180° | Camada externa com dobra dupla de 90° | Tamanho mínimo de curvatura H | Tamanho mínimo da curva em Z (Z) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8.0 | 12.0 | R1 | 0.6 | 0.2 | 0.5 | 0.9 | 1.0 | 0.7 | 0.2 | 0.3 | 1.9 | 6.0 | 10.0 |
| 0.8 | 0.3 | 0.6 | 1.0 | 1.6 | 0.8 | 0.3 | 0.4 | 2.2 | |||||
| 1 | 0.3 | 0.7 | 1.1 | 1.7 | 0.9 | 0.3 | 0.5 | 2.5 | |||||
| 1.2 | 0.4 | 0.8 | 1.3 | 2.2 | 1.1 | 0.4 | 0.6 | 2.8 | |||||
| R2 | 0.6 | 0.2 | 0.5 | 0.9 | 1.6 | 0.7 | 0.2 | 0.3 | 1.9 | ||||
| 0.8 | 0.3 | 0.6 | 1.2 | 1.8 | 0.8 | 0.3 | 0.4 | 2.2 | |||||
| 1 | 0.3 | 0.7 | 1.2 | 2.0 | 0.9 | 0.3 | 0.5 | 2.5 | |||||
| 1.2 | 0.4 | 0.8 | 1.4 | 2.3 | 1.1 | 0.4 | 0.6 | 2.8 | |||||
| 10.0 | 14.0 | R1 | 1.5 | 0.7 | 1.2 | 1.6 | 2.5 | 1.3 | 0.5 | 0.7 | 3.2 | 7.0 | 11.0 |
| R2 | 1.5 | 0.6 | 1.0 | 1.5 | 2.7 | 1.3 | 0.5 | 0.7 | 3.5 | ||||
| 12.0 | 16.0 | R1 | 2 | 0.6 | 1.3 | 2.0 | 3.4 | 1.7 | 0.6 | 0.9 | 4.4 | 8.5 | 13.0 |
| R2 | 2 | 0.9 | 1.4 | 2.0 | 3.6 | 1.7 | 0.6 | 0.9 | 4.5 | ||||
| 16.0 | 26.0 | R1 | 2.5 | 0.7 | 1.5 | 2.4 | 4.3 | 2.2 | 0.8 | 1.1 | 5.6 | 12.0 | 20.0 |
| 3 | 0.8 | 1.7 | 2.8 | 5.1 | 2.8 | 0.8 | 1.3 | 5.8 | |||||
| R2 | 2.5 | 0.8 | 1.6 | 2.5 | 4.8 | 2.3 | 0.9 | 1.1 | 6.2 | ||||
| 3 | 1.0 | 2.0 | 3.0 | 5.2 | 2.8 | 1.0 | 1.3 | 6.4 | |||||
| 22.0 | 32.5 | R1 | 4 | 1.0 | 2.4 | 3.5 | 6.5 | 3.3 | 1.1 | 16.0 | 26.0 | ||
| R2 | 4 | 1.2 | 2.6 | 4.0 | 6.8 | 3.5 | 1.1 | ||||||
| 32.0 | 50.0 | R1 | 5 | 1.2 | 3.2 | 4.8 | 8.6 | 4.6 | 1.4 | 24.0 | 38.0 | ||
| 6 | 1.5 | 3.5 | 4.5 | 9.5 | 5.0 | 1.8 | |||||||
| R2 | 5 | 1.5 | 3.4 | 5.0 | 8.8 | 4.5 | 1.6 | ||||||
| 6 | 1.8 | 3.8 | 5.5 | 9.8 | 5.2 | 2.0 |

Explicação:
| Fórmula | 0.2t | 0.4t | 0.6t | 0.8t | 1.0t | 1.2t | 1.4t | 1.6t |
| Ângulo | 155-165° | 145-155° | 135-145° | 125-135° | 115-125° | 105-115° | 95-105° | 85-95° |
| Espessura (t) | 15-25° | 25-35° | 35-45° | 45-55° | 55-65° | 65-75° | 75-85° | |
| 0.5 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 |
| 0.6 | 0.12 | 0.24 | 0.36 | 0.48 | 0.60 | 0.72 | 0.84 | 0.96 |
| 0.8 | 0.16 | 0.32 | 0.48 | 0.64 | 0.80 | 0.96 | 1.12 | 1.28 |
| 1.0 | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 | 1.20 | 1.40 | 1.60 |
| 1.2 | 0.24 | 0.48 | 0.72 | 0.96 | 1.20 | 1.44 | 1.68 | 1.92 |
| 1.5 | 0.30 | 0.60 | 0.90 | 1.20 | 1.50 | 1.80 | 2.10 | 2.40 |
| 2.0 | 0.40 | 0.80 | 1.20 | 1.60 | 2.00 | 2.40 | 2.80 | 3.20 |
| 2.5 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 | 4.00 |
| 3.0 | 0.60 | 1.20 | 1.80 | 2.40 | 3.00 | 3.60 | 4.20 | 4.80 |
| 4.0 | 0.80 | 1.60 | 2.40 | 3.20 | 4.00 | 4.80 | 5.60 | 6.40 |
| 4.5 | 0.90 | 1.80 | 2.70 | 3.60 | 4.50 | 5.40 | 6.30 | 7.20 |
| 5.0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 | 7.00 | 8.00 |
| 6.0 | 1.20 | 2.40 | 3.60 | 4.80 | 6.00 | 7.20 | 8.40 | 9.60 |
| Fórmula | 0.3t | 0.5t | 0.7t | 0.9t | 1.1t | 1.3t | 1.5t | 1.7t |
| Ângulo | 155-165° | 145-155° | 135-145° | 125-135° | 115-125° | 105-115° | 95-105° | 85-95° |
| Espessura (t) | 15-25° | 25-35° | 35-45° | 45-55° | 55-65° | 65-75° | 75-85° | |
| 0.5 | 0.15 | 0.25 | 0.35 | 0.45 | 0.55 | 0.65 | 0.75 | 0.85 |
| 0.6 | 0.18 | 0.30 | 0.42 | 0.54 | 0.66 | 0.78 | 0.90 | 1.02 |
| 0.8 | 0.24 | 0.40 | 0.56 | 0.72 | 0.88 | 1.04 | 1.20 | 1.36 |
| 1.0 | 0.30 | 0.50 | 0.70 | 0.90 | 1.10 | 1.30 | 1.50 | 1.70 |
| 1.2 | 0.36 | 0.60 | 0.84 | 1.08 | 1.32 | 1.56 | 1.80 | 2.04 |
| 1.5 | 0.45 | 0.75 | 1.05 | 1.35 | 1.65 | 1.95 | 2.25 | 2.55 |
| 2.0 | 0.60 | 1.00 | 1.40 | 1.80 | 2.20 | 2.60 | 3.00 | 3.40 |
| 2.5 | 0.75 | 1.25 | 1.75 | 2.25 | 2.75 | 3.25 | 3.75 | 4.25 |
| 3.0 | 0.90 | 1.50 | 2.10 | 2.70 | 3.30 | 3.90 | 4.50 | 5.10 |
| 4.0 | 1.20 | 2.00 | 2.80 | 3.60 | 4.40 | 5.20 | 6.00 | 6.80 |
| 4.5 | 1.35 | 2.25 | 3.15 | 4.05 | 4.95 | 5.85 | 6.75 | 7.65 |
| 5.0 | 1.50 | 2.50 | 3.50 | 4.50 | 5.50 | 6.50 | 7.50 | 8.50 |
| 6.0 | 1.80 | 3.00 | 4.20 | 5.40 | 6.60 | 7.80 | 9.00 | 10.20 |
| Não. | Ângulo /Espessura | 0.8 | 1.0 | 1.2 | 1.5 | 2.0 | 2.5 | 3.0 | 4.0 | 5.0 |
| 1 | 0 | 3.00 | 3.60 | 4.00 | 5.00 | 7.00 | 8.40 | 10.00 | 14.00 | 20.00 |
| 2 | 5 | 2.92 | 3.50 | 3.89 | 4.86 | 6.81 | 8.17 | 9.72 | 13.61 | 19.44 |
| 3 | 10 | 2.83 | 3.40 | 3.78 | 4.72 | 6.61 | 7.93 | 9.44 | 13.22 | 18.89 |
| 4 | 15 | 2.75 | 3.30 | 3.67 | 4.58 | 6.42 | 7.70 | 9.17 | 12.83 | 18.33 |
| 5 | 20 | 2.67 | 3.20 | 3.56 | 4.44 | 6.22 | 7.47 | 8.89 | 12.44 | 17.78 |
| 6 | 25 | 2.58 | 3.10 | 3.44 | 4.31 | 6.03 | 7.23 | 8.61 | 12.06 | 17.22 |
| 7 | 30 | 2.50 | 3.00 | 3.33 | 4.17 | 5.83 | 7.00 | 8.33 | 11.67 | 16.67 |
| 8 | 35 | 2.42 | 2.90 | 3.22 | 4.03 | 5.64 | 6.77 | 8.06 | 11.28 | 16.11 |
| 9 | 40 | 2.33 | 2.80 | 3.11 | 3.89 | 5.44 | 6.53 | 7.78 | 10.89 | 15.56 |
| 10 | 45 | 2.25 | 2.70 | 3.00 | 3.75 | 5.25 | 6.30 | 7.50 | 10.50 | 15.00 |
| 11 | 50 | 2.17 | 2.60 | 2.89 | 3.61 | 5.06 | 6.07 | 7.22 | 10.11 | 14.44 |
| 12 | 55 | 2.08 | 2.50 | 2.78 | 3.47 | 4.86 | 5.83 | 6.94 | 9.72 | 13.89 |
| 13 | 60 | 2.00 | 2.40 | 2.67 | 3.33 | 4.67 | 5.60 | 6.67 | 9.33 | 13.33 |
| 14 | 65 | 1.92 | 2.30 | 2.56 | 3.19 | 4.47 | 5.37 | 6.39 | 8.94 | 12.78 |
| 15 | 70 | 1.83 | 2.20 | 2.44 | 3.06 | 4.28 | 5.13 | 6.11 | 8.56 | 12.22 |
| 16 | 75 | 1.75 | 2.10 | 2.33 | 2.92 | 4.08 | 4.90 | 5.83 | 8.17 | 11.67 |
| 17 | 80 | 1.67 | 2.00 | 2.22 | 2.78 | 3.89 | 4.67 | 5.56 | 7.78 | 11.11 |
| 18 | 85 | 1.58 | 1.90 | 2.11 | 2.64 | 3.69 | 4.43 | 5.28 | 7.39 | 10.56 |
| 19 | 90 | 1.50 | 1.80 | 2.00 | 2.50 | 3.50 | 4.20 | 5.00 | 7.00 | 10.00 |
| 20 | 95 | 1.42 | 1.70 | 1.89 | 2.36 | 3.31 | 3.97 | 4.72 | 6.61 | 9.44 |
| 21 | 100 | 1.33 | 1.60 | 1.78 | 2.22 | 3.11 | 3.73 | 4.44 | 6.22 | 8.89 |
| 22 | 105 | 1.25 | 1.50 | 1.67 | 2.08 | 2.92 | 3.50 | 4.17 | 5.83 | 8.33 |
| 23 | 110 | 1.17 | 1.40 | 1.56 | 1.94 | 2.72 | 3.27 | 3.89 | 5.44 | 7.78 |
| 24 | 115 | 1.08 | 1.30 | 1.44 | 1.81 | 2.53 | 3.03 | 3.61 | 5.06 | 7.22 |
| 25 | 120 | 1.00 | 1.20 | 1.33 | 1.67 | 2.33 | 2.80 | 3.33 | 4.67 | 6.67 |
| 26 | 125 | 0.92 | 1.10 | 1.22 | 1.53 | 2.14 | 2.57 | 3.06 | 4.28 | 6.11 |
| 27 | 130 | 0.83 | 1.00 | 1.11 | 1.39 | 1.94 | 2.33 | 2.78 | 3.89 | 5.56 |
| 28 | 135 | 0.75 | 0.90 | 1.00 | 1.25 | 1.75 | 2.10 | 2.50 | 3.50 | 5.00 |
| 29 | 140 | 0.67 | 0.80 | 0.89 | 1.11 | 1.56 | 1.87 | 2.22 | 3.11 | 4.44 |
| 30 | 145 | 0.58 | 0.70 | 0.78 | 0.97 | 1.36 | 1.63 | 1.94 | 2.72 | 3.89 |
| 31 | 150 | 0.50 | 0.60 | 0.67 | 0.83 | 1.17 | 1.40 | 1.67 | 2.33 | 3.33 |
| 32 | 155 | 0.42 | 0.50 | 0.56 | 0.69 | 0.97 | 1.17 | 1.39 | 1.94 | 2.78 |
| 33 | 160 | 0.33 | 0.40 | 0.44 | 0.56 | 0.78 | 0.93 | 1.11 | 1.56 | 2.22 |
| 34 | 165 | 0.25 | 0.30 | 0.33 | 0.42 | 0.58 | 0.70 | 0.83 | 1.17 | 1.67 |
| 35 | 170 | 0.17 | 0.20 | 0.22 | 0.28 | 0.39 | 0.47 | 0.56 | 0.78 | 1.11 |
| 36 | 175 | 0.08 | 0.10 | 0.11 | 0.14 | 0.19 | 0.23 | 0.28 | 0.39 | 0.56 |
| 37 | 180 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |

1) A tabela de dedução de dobra é aplicável a processos de dobra de chapas metálicas em que não se usa placa de prensagem e a largura da chapa é superior a três vezes a espessura (t).
2) Ao dobrar na máquina de dobra, os cálculos podem ser feitos de acordo com esta tabela.
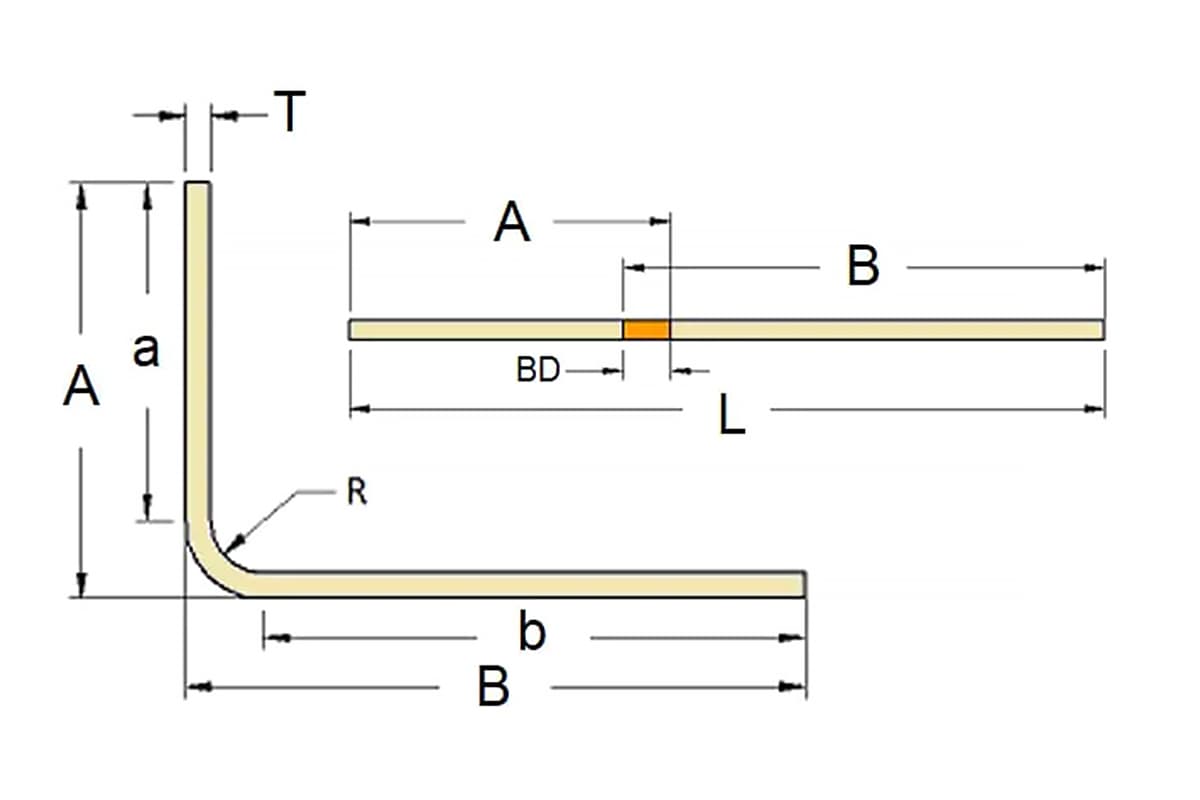
3) De acordo com as dimensões indicadas no diagrama, a fórmula de cálculo para o tamanho desdobrado da peça de trabalho dobrada é a seguinte:
L=a+b-y
Onde:
4) Devido aos inúmeros fatores que influenciam o dobramento de chapas metálicas, esta tabela de valores de dedução de dobramento de chapas metálicas é fornecida apenas como referência.
A precisão dimensional das peças dobradas está relacionada à precisão posicional do medidor traseiro da prensa dobradeira e à precisão da chapa máquina de corte de metal. A utilização de máquinas confiáveis para os processos de corte e dobra pode resolver esses problemas.
Um fator crítico que afeta a precisão dimensional das peças de trabalho dobradas é a precisão do desenvolvimento do padrão plano da chapa metálica. Quando uma chapa plana é dobrada em uma peça de trabalho com um ângulo específico, a medição das dimensões da peça de trabalho dobrada revela que elas não são iguais às dimensões da chapa plana, conforme mostrado na ilustração.
Essa discrepância é conhecida como dedução de flexão.
Se a dedução de dobra for imprecisa, o tamanho do padrão plano será impreciso e, independentemente da precisão das operações subsequentes, a peça final não atenderá à precisão dimensional necessária.

A dedução de flexão é complexa, e um método rudimentar é simplesmente usar o dobro da espessura do material.
Entretanto, essa abordagem é bastante rudimentar. Um método mais refinado é aplicar a teoria do eixo neutro da norma DIN 6935, que envolve o cálculo de um fator "k" e sua combinação com a espessura e o ângulo da chapa a ser dobrada.
Essa fórmula produz uma dedução de flexão mais precisa. No entanto, mesmo as deduções de flexão calculadas de acordo com a teoria do eixo neutro da norma DIN 6935 podem não ser suficientemente precisas, pois as deduções reais também dependem das características do material, da espessura, da ângulo de flexãoe as ferramentas utilizadas.
Diferentes materiais, espessuras e métodos de cálculo geram diferentes deduções de flexão, conforme mostrado na tabela abaixo.
Tabela Valor de dedução para dimensões de dobra correspondentes a diferentes materiais, espessuras e métodos
| Espessura da placa S/mm | Morrer | Material | -S × 2 | DIN6935 | Banco de dados |
| 1.5 | V12/78 | DC04 | -3.00 | -3.00 | -2.90 |
| 1.5 | V08/78 | DC04 | -3.00 | -2.80 | -2.70 |
| 1.5 | V1278 | X5CrNi1810 | -3.00 | -3.00 | -3.10 |
| 4 | V24/78 | S235JRG2 | -8.00 | -7.60 | -7.09 |
| 4 | V30/78 | S235JRG2 | -8.00 | -7.57 | -7.26 |
| 4 | V24/78 | X5CrNi1810 | -8.00 | -8.01 | -7.57 |
| 4 | V30/78 | X5CrNi1810 | -8.00 | -7.90 | -8.01 |
| 6 | V30/78 | S235JRG2 | -12.00 | -11.20 | -10.35 |
| 6 | V4078 | S235JRG2 | -12.00 | -11.60 | -10.62 |
| 6 | V30/78 | X5CrNi1810 | -12.00 | -11.20 | -10.89 |
| 6 | V4078 | X5CrNi1810 | -12.00 | -11.60 | -11.60 |
Por exemplo, para uma placa S235JRG2 de 4 mm de espessura usando uma matriz inferior V30, a dedução de flexão varia de acordo com o método: duas vezes a espessura do material resulta em 8 mm, a fórmula DIN 6935 produz 7,57 mm e o valor empírico do banco de dados fornece 7,26 mm.
Há discrepâncias entre os métodos, que se tornam ainda mais significativas quando as peças de trabalho exigem várias dobras, o que leva a desvios cumulativos maiores. Os valores empíricos do banco de dados são derivados de extensos testes práticos e são armazenados no banco de dados, proporcionando a máxima precisão.