Como uma viga de aço suporta o peso de uma ponte ou a pressão de um guindaste? Este artigo se aprofunda nos cálculos de resistência à flexão da seção de aço, explicando os conceitos de estágios elástico, elástico-plástico e plástico. Ao compreender a resistência e a rigidez de diferentes seções, os leitores aprenderão como garantir a segurança e a estabilidade das estruturas sob várias cargas. Mergulhe de cabeça para compreender os princípios fundamentais que mantêm nossas construções firmes e resistentes.
1. Conceito:
Suporta cargas laterais, como vigas de piso, vigas de guindaste, madres, pontes etc.
2. Classificação:
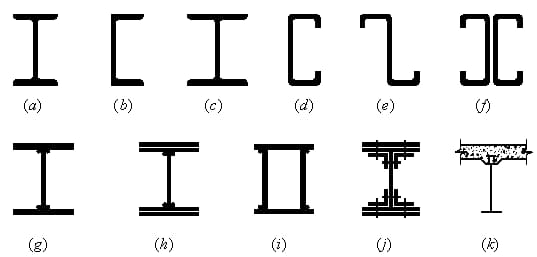
(1) Rede sólida：
Seção de aço em forma de H: Fácil de processar, simples de fabricar e de baixo custo.
Seção composta: Quando o aço em forma de H não puder atender aos requisitos de resistência e rigidez.
(2) Estrutura da rede:
Quando o vão exceder 40 m, é melhor usar uma treliça.
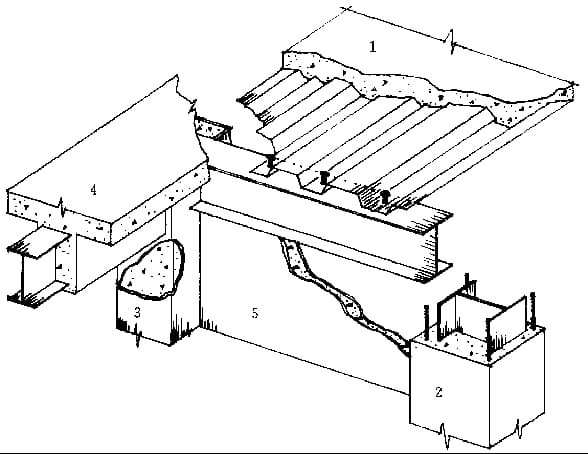
3. Grade de feixes:
Um sistema plano composto por vigas principais e secundárias que se cruzam vertical e horizontalmente.
(1) Grade de feixe simplificada: Feixe principal único.
(2) Grade de viga comum: Dividida em vigas principais e secundárias.
(3) Grade de vigas compostas: Dividida em vigas principais, vigas secundárias horizontais e verticais.
4. Interação entre vigas e placas:
(1) Co-working: Laje de piso composta.
(2) Trabalho não cooperativo: Laje de concreto reforçado geral.
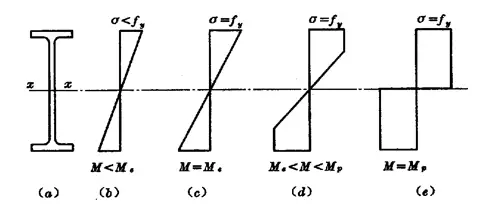
O desenvolvimento da tensão normal na seção transversal pode ser dividido em três estágios:
(1) Estágio elástico: Sob carga dinâmica.
(2) Estágio elástico-plástico: Sob carga estática ou carga dinâmica indireta.
(3) Estágio de plástico:
Capacidade de flexão durante o estágio elástico-plástico de uma seção transversal:
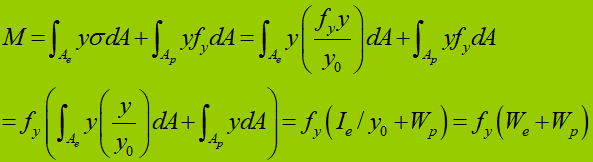
Para uma seção retangular:
(1) Estágio elástico:
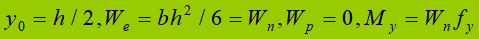
(2) Estágio de plástico:
(3) Estágio elástico-plástico:
Fator de forma da seção:
Desenvolvimento plástico de seção parcial (1/4 de seção, a = h/8) como estado limite:
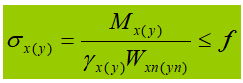
Na fórmula:
γ é o fator de segurança parcial para o momento, que pode ser determinado com base na Tabela 5.1 na Seção 5 do código de projeto.
Há dois casos em que o fator de segurança parcial para o momento deve ser considerado como 1,0.
Método:
S:
A resistência ao cisalhamento pode ser calculada usando a teoria do fluxo de cisalhamento, supondo que ela seja distribuída uniformemente ao longo da direção da espessura da parede fina.
(1) Ao calcular a tensão de cisalhamento vertical em qualquer ponto da trama, é necessário calcular o momento de inércia da área da seção bruta acima ou abaixo desse ponto em relação ao eixo neutro x.
(2) Ao calcular a tensão de cisalhamento horizontal em qualquer ponto do flange, é necessário calcular o momento de inércia da área da seção bruta à esquerda ou à direita desse ponto em relação ao eixo neutro x.
Onde tw é a espessura da seção no local em que a tensão de cisalhamento está sendo calculada.
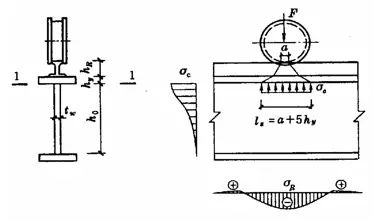
Quando o flange de uma viga é submetido a uma grande carga central fixa (incluindo reações de apoio) e não há reforços, de acordo com a Figura 5-5 (a), ou quando é submetido a uma carga concentrada móvel (como a pressão da roda do guindaste), de acordo com a Figura 5-5 (b), a resistência à compressão local na borda da altura da alma deve ser calculada. Supondo que a carga concentrada se espalhe do ponto de aplicação para uma faixa de altura de hy em uma proporção de 1:2,5, e se espalha em uma proporção de 1:1 em uma faixa de altura de hRe é distribuído uniformemente sobre a altura da teia cálculo da borda. O σc é muito próximo da pressão local teórica máxima. A resistência à compressão local pode ser calculada pela seguinte fórmula:
Na fórmula,
Quando o cálculo não for satisfatório, o suporte ou a carga concentrada fixa do rolamento pode ser reforçado com a instalação de reforços transversais ou com a modificação do tamanho da seção. Entretanto, ao suportar cargas concentradas móveis, somente o tamanho da seção pode ser modificado.
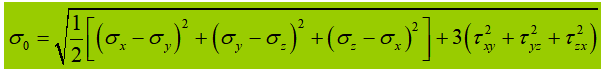
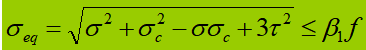
Quando o vibrador de abdômen é submetido a uma tensão normal significativa, tensão de cisalhamento ou tensão de compressão local na altura calculada, a tensão equivalente nesse local precisa ser calculada.
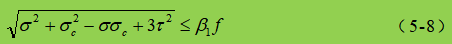
Na fórmula:
σ, τ, σc - tensão normal de flexão, tensão de cisalhamento e tensão de compressão local no mesmo ponto da altura de cálculo da placa do abdome, positiva para tensão de tração e negativa para tensão de compressão;
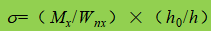
β1 - coeficiente para aumentar o valor de projeto da resistência à compressão em um ponto local. Quando σ e σc têm o mesmo sinal ou σc=0, β1=1,1; quando σ e σc têm sinais opostos, β1=1.2.
Fenômeno de instabilidade geral:
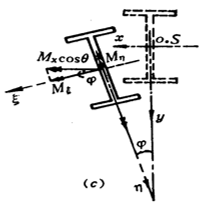
Análise do mecanismo:
Depois que a viga é deformada por flexão, o flange superior é submetido à compressão. Devido à rigidez lateral insuficiente da viga, a viga sofrerá uma deformação de flambagem lateral. A deformação de flexão no plano causada pelo momento também ocorre junto com a deformação de torção devido à flexão desigual de cima para baixo da seção da viga.
Portanto, a instabilidade geral da viga assume a forma de encurvadura por flexão-torção ou, mais precisamente, encurvadura por flexão lateral e torção.
(1) C1, C2, C3 - Relacionado ao tipo de carga
(2) Iy, Iw, It - Momento de inércia da seção transversal
(3) L - Comprimento sem suporte na direção lateral
(4) a - Localização do ponto de ação na direção da altura.
(5) 
| Condição de carga | Coeficiente | ||
| G | C2 | G | |
| Carga concentrada no meio do vão | 1.35 | 0.55 | 0.41 |
| Carga uniformemente distribuída em todo o vão | 1.13 | 0.46 | 0.53 |
| Flexão pura | 1.00 | 0.00 | 1.00 |
Os principais fatores que afetam a estabilidade geral das vigas de aço são:
(1) O comprimento sem contraventamento na direção lateral ou a distância L1 entre o ponto de apoio lateral do flange comprimido. Quanto menor for o valor de L1, melhor será a estabilidade geral da viga e maior será o momento de flexão crítico.
(2) O tamanho da seção transversal, incluindo vários momentos de inércia. Quanto maior for o momento de inércia, melhor será a estabilidade geral da viga. Em particular, o aumento da largura do flange comprimido b1 também pode aumentar o valor de βy na fórmula.
(3) As restrições na seção pelos suportes das extremidades da viga. Se as restrições sobre a rotação em torno do eixo y da seção puderem ser melhoradas, a estabilidade geral da viga será bastante aprimorada.
(4) Tipo de carregamento: Flexão pura, carga uniformemente distribuída, carga concentrada no meio do vão.
(5) A localização do ponto de ação da carga ao longo da direção da altura da seção transversal, um valor; negativo para o flange superior e positivo para o flange inferior.
Flexão em um único plano:
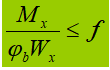
1. Seção transversal soldada em forma de I, biaxialmente simétrica, pura carga de flexão.
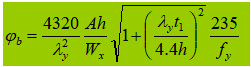
2. Seção transversal soldada em forma de I, uniaxialmente simétrica (efeitos da seção transversal assimétrica e cargas diferentes)
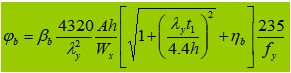
Se φb>0,6, o coeficiente de estabilidade é considerado como:
3. Viga laminada de aço comum em forma de I com suporte simples.
4. Viga com suporte simples de canal de aço laminado a quente.
5. Uma viga cantilever em forma de I simétrica de eixo duplo.
O flange comprimido da viga é coberto com um deck (concreto reforçado ou chapa de aço) e firmemente conectados para evitar o deslocamento lateral do flange comprimido.
Para vigas H ou I simplesmente apoiadas, a relação entre o comprimento livre L1 e a largura b do flange comprimido não excede o valor especificado na Tabela 5.4.
Tabela 5.4: Valor máximo de L1/b1 para o qual o cálculo de estabilidade geral não é necessário para vigas H ou I simplesmente apoiadas.
| Grau de aço | Uma viga sem pontos de apoio lateral no meio do vão. | Uma viga com um flange sujeito à compressão ao longo do vão e com pontos de apoio laterais, independentemente de onde a carga é aplicada. | |
| A carga é aplicada ao flange. | A carga é aplicada ao flange inferior. | ||
| Q235 | 13.0 | 20.0 | 16.0 |
| Q345 | 10.5 | 16.5 | 13.0 |
| Q39 | 10.0 | 15.5 | 12.5 |
| Q420 | 9.5 | 15.0 | 12.0 |
1. Determine se a verificação da estabilidade geral é necessária.
2. Calcule os parâmetros da seção.
3. obtenha o coeficiente de momento de flexão crítico equivalente βb de acordo com as condições de carga.
4. Substitua os valores nas fórmulas para obter o coeficiente de estabilidade geral ϕb e verifique a estabilidade geral.
Exemplo: 5-2，5-3
Placa de flange: A carga é relativamente simples, e a estabilidade local é garantida pela limitação da relação entre largura e espessura da placa.
Placa da Web: A carga é complexa e, para atender aos requisitos de resistência, a altura da seção geralmente é grande. Se continuarmos a limitar a relação altura/espessura da placa da alma, o valor da placa da alma será muito grande, o que não é econômico. Portanto, os reforços são geralmente usados para reduzir o tamanho da placa e melhorar a capacidade de suporte da estabilidade local.
1. Reforços transversais
2. Reforços longitudinais
3. Reforços curtos
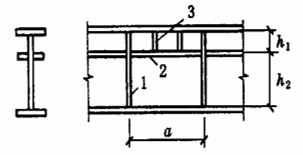
Princípio do projeto: princípio da força igual.
De acordo com o projeto elástico (com γ=1,0 para não considerar o desenvolvimento plástico), devido à influência de tensão residuala seção transversal real entrou no estágio elástico-plástico. A "Especificação" assume Et=0.7E.
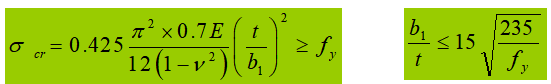
Se o desenvolvimento plástico for considerado (γ > 1,0), o desenvolvimento plástico será maior, e Et=0.5E.
| Não. | A condição da placa de rede. | Especificações do arranjo dos reforços | |
| 1 | 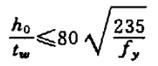 | στ=0 | Os reforços podem ser omitidos. |
| 2 | στ≠0 | Recomenda-se a instalação de reforços transversais que atendam aos requisitos estruturais e de cálculo. | |
| 3 |  | Recomenda-se a instalação de reforços transversais que atendam aos requisitos estruturais e de cálculo. | |
| 4 |  O flange comprimido é restringido contra torção. | Os reforços longitudinais devem ser adicionados na zona de compressão da seção, onde a tensão de flexão é alta, atendendo aos requisitos estruturais e de cálculo. | |
| 5 | 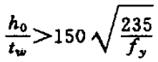 O flange comprimido está livre para torcer. | ||
| 6 | Quando necessário para fins de cálculo. | ||
| 7 | Quando a tensão compressiva local é alta. | Se necessário, reforços curtos devem ser dispostos na zona de compressão para atender aos requisitos estruturais e de cálculo. | |
| 8 | No suporte da viga | É recomendável instalar reforços de suporte que atendam aos requisitos estruturais e de cálculo. | |
| 9 | Quando o flange é submetido a uma grande carga concentrada fixa. | ||
| 10 | De qualquer forma |  | |
1. Encurvadura de placas compostas tensionadas
Somente a placa da alma com reforços transversais está configurada.
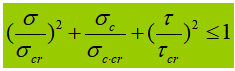
A placa da alma é configurada com reforços transversais e longitudinais ao mesmo tempo.
(1) Entre o flange comprimido e os reforços longitudinais.
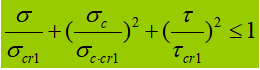
(2) Entre o flange de tensão e os reforços longitudinais.
Os reforços transversais curtos são instalados entre o flange comprimido e os reforços longitudinais.
2. Requisitos de construção de reforços para chapas de aço
(1) Reforços transversais de aço configurados em pares em ambos os lados da placa da alma.
Largura protuberante para fora:
Espessura:
(2) Reforços transversais de aço configurados em um lado da placa da alma.
Largura protuberante externa: deve ser maior que 1,2 vezes o valor calculado de acordo com a fórmula acima.
Espessura: não deve ser inferior a 1/15 de sua largura protuberante externa.
(3) Na placa da alma reforçada com reforços transversais e longitudinais, os reforços longitudinais devem ser desconectados em suas interseções, enquanto os reforços transversais permanecem contínuos.
O momento de inércia em torno do eixo z também deve satisfazer:
(4) Tratamento da extremidade dos reforços transversais:
3. Reforços para suporte
(1) Cálculo da estabilidade:
A estabilidade dos reforços para suporte é calculada como um membro de compressão sujeito a cargas concentradas fixas ou reações de suporte de viga ao longo de seu eixo. A área da seção transversal A desse membro de compressão inclui tanto o reforço quanto a área da placa da alma dentro de 15tw em cada lado do reforço. O comprimento de cálculo é considerado aproximadamente como h0.
(2) Cálculo da resistência à compressão:
A extremidade dos reforços de suporte da viga deve ser calculada de acordo com a carga concentrada fixa ou a reação de suporte que eles suportam. Quando a extremidade dos reforços é cortada de forma plana e firme, a tensão de compressão na face da extremidade deve ser calculada da seguinte forma:
onde:
Etapas de projeto para reforços transversais de chapas de aço:
1. Determine se é necessário instalar barras transversais;
2. Instale as barras transversais e determine o espaçamento a, bs, ts;
3. Verifique o estado de tensão composto da placa da alma;
4. Verifique o reforço de suporte: incluindo a solda (conexão entre as barras transversais e a placa da alma), verificação da estabilidade da compressão axial (estabilização fora do plano do eixo z) e verificação da resistência.
Exemplo 5-3: Com base nas condições e nos resultados do Exemplo 5-2, verifique se a seção da viga principal mostrada na Figura 5-9(b) atende aos requisitos. A viga principal é uma viga simplesmente apoiada em ambas as extremidades, feita de aço Q235 e soldada com eletrodos de solda manual da série E43.
Solução:
1. Capacidade de suporte de carga da viga principal:
O diagrama de cálculo simplificado da viga principal é mostrado na Figura 5-9(a). A pressão exercida na viga principal pelas vigas secundárias em ambos os lados é de 2×73,69+2×2,33=152,04 kN, e a pressão das vigas secundárias na extremidade da viga é a metade da pressão da viga secundária do meio.
A reação de apoio da viga principal é R=2×152,04=304,08 kN.
O momento de flexão máximo da viga é M=(304,08-76,02)x5-152,04×2,5=760,2 kN.m
2. Calcule as características da seção:
A=131,2 cm², Ix=145449 cm⁴, Wx=3513,3 cm³. O peso próprio da viga principal é 131,2×10²x7850x10-⁶x1,2=123,6 kg/m=1,211 kN/m. O fator de 1,2 é para considerar o aumento do coeficiente do reforço da viga principal. O valor de projeto do momento de flexão após considerar o peso da viga principal é M=760,2+1,2×1,211×10²/8=760,2+18,2=778,4 kN-m.
Considerando que o valor do projeto da força de reação no suporte após a contabilização do peso próprio da viga principal é R=304,08+1,2×1,211×10/2=304,08+7,27=311,3kN.
3. Verificação de força
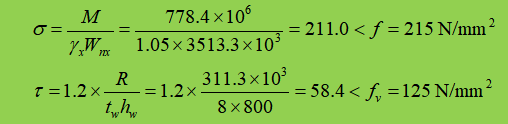
Os reforços de suporte são fornecidos na conexão da viga secundária, e não há tensão de compressão local. Além disso, como a tensão de cisalhamento é relativamente pequena, não há necessidade de verificar outras tensões convertidas em seção.
4. Há uma placa rígida na viga secundária, que garante a estabilidade da viga secundária e pode servir como um ponto de apoio lateral para a viga principal.
Nesse ponto, como l1/b1=2500/240=10,4<16, a estabilidade geral pode ser garantida sem cálculos.
5. Verificação da rigidez
O valor padrão total da carga transmitida pela viga secundária é FT=(15.5+0.52)×7.5=120.2kN, therefore,
O valor padrão total da carga transmitida pela viga secundária é FQ=2.5×4.2×7.5=78.75kN, therefore,
6. Estabilidade local
Flange: b/t=(120-4)/14=8,3<13, que atende ao requisito de estabilidade local, e γx pode ser considerado como 1,05; Placa da Web: h0/tw=800/8=100, os reforços transversais precisam ser fornecidos, os detalhes são omitidos.
Depois que a placa fina se dobra, são geradas tensões de tração transversais no meio da placa, o que restringe ainda mais a deformação de flexão longitudinal da placa, permitindo que ela continue a suportar o aumento da pressão.
1. Capacidade de suporte de cisalhamento após a flambagem: Fórmula (5-94)
2. A capacidade de suporte de cisalhamento inclui duas partes: Força de cisalhamento de flambagem (resistência à flambagem) + força de cisalhamento do campo de tensão (resistência após a flambagem).
3. Força de cisalhamento do campo de tensão:
(1) Método do campo de tensão (complexo);
(2) Especificação do código.
Considerando que a capacidade de suporte de flexão da placa da alma diminui ligeiramente após a flambagem.
Duas suposições:
(1) Altura efetiva;
(2) Simetria entre a zona de tensão e a zona de compressão.
A fórmula para calcular a capacidade de suporte:
Na fórmula,
Isso indica que:
(1) Quando M na seção for menor que Mf que o flange pode suportar, a placa da alma pode suportar a força de cisalhamento Vu;
(2) Quando V na seção for menor que 0,5Vu, considere M = Meu.
(1) Se os reforços de suporte sozinhos não puderem satisfazer a Equação (5.99), reforços transversais emparelhados devem ser adicionados em ambos os lados da alma para reduzir o comprimento da região de flambagem.
(2) As dimensões da seção transversal dos reforços transversais devem atender aos requisitos de construção para os reforços da alma, conforme a Equação 5.85.
(3) De acordo com as especificações da estrutura de aço, o reforço transversal central deve ser tratado como um membro de compressão axial e sua estabilidade fora do plano da alma deve ser calculada com base na força axial usando a seguinte fórmula:
Quando o reforço é submetido a uma carga transversal concentrada F, Ns deve ser aumentado em F.
Calcule o valor de projeto do momento de flexão máximo Mmáximo para a viga com base nas condições reais.
Determine o módulo de seção necessário com base na resistência à flexão e na estabilidade geral:
Determine a seção do aço com base nas tabelas de seção.
Verificação da seção:
(1) Verificação da resistência: flexão, cisalhamento, compressão local e tensão equivalente.
(2) Verificação da rigidez: verifique a relação entre a deflexão e o vão da viga.
(3) Verificação da estabilidade geral (a estabilidade local da seção de aço geralmente não requer verificação).
(4) Ajuste a seção com base nos resultados da verificação e faça a verificação novamente até que ela atenda aos requisitos do projeto.
1) Determine o módulo de seção necessário com base nas condições de carga.
2) Determine a altura do feixe:
Altura selecionada: hmin ≤ h ≤ hmáximo.
3). Determine a espessura da alma (supondo que todas as forças de cisalhamento sejam suportadas pela alma):
Como alternativa, a espessura da tela pode ser determinada por meio de fórmulas empíricas:
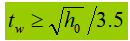
4). Determine a largura do flange:
Após determinar a espessura da alma, a área do flange Af pode ser determinado com base nos requisitos de resistência à flexão. Tomando como exemplo uma seção em forma de I:
Uma vez Af é determinado, b ou t pode ser selecionado para determinar o outro valor.
5). Verificação da seção:
6). Cálculo de soldas entre a alma e o flange
A solda de conexão é usada principalmente para resistir a flexão e cisalhamentoe o cisalhamento por unidade de comprimento é:
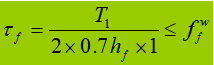
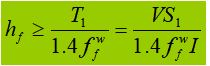
Quando a viga é submetida a uma carga concentrada fixa sem reforços de suporte, a solda do flange superior suporta a força de cisalhamento T1 e a força concentrada F. A força por unidade de comprimento gerada por F é V1:
Objetivo: Para economizar aço e lidar com as mudanças no momento de flexão.
Métodos de alteração de seção:
Pontos a serem observados:
1. Classificação:
2. Métodos de emenda para seções de aço laminadas:
3. Técnicas de emenda de vigas compostas:
Principais considerações:
1. Conexões primárias e secundárias de vigas de aço:
2. Tipos de suporte de viga:
Principais considerações sobre o projeto:
Como fundador do MachineMFG, dediquei mais de uma década de minha carreira ao setor de metalurgia. Minha vasta experiência permitiu que eu me tornasse um especialista nas áreas de fabricação de chapas metálicas, usinagem, engenharia mecânica e máquinas-ferramentas para metais. Estou sempre pensando, lendo e escrevendo sobre esses assuntos, esforçando-me constantemente para permanecer na vanguarda do meu campo. Permita que meu conhecimento e experiência sejam um trunfo para sua empresa.
PT_BR 
EN 
AR 
DE 
ES 
FR 
IT 
JA 
NL 
PT 
RU 
KO