Gráfico de força de flexão de ar (Amada)
Nesta postagem do blog, exploraremos o fascinante mundo da flexão de ar e os gráficos de força que tornam isso possível. Junte-se a nós enquanto nos aprofundamos na ciência por trás desse...
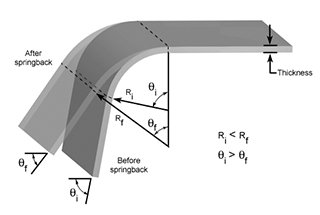
Você já se perguntou como calcular com precisão a força de flexão necessária para a fabricação de chapas metálicas? Nesta postagem perspicaz do blog, exploraremos os meandros do cálculo da força de flexão, com base na experiência de engenheiros mecânicos experientes. Descubra os principais fatores que influenciam a força de flexão e saiba como aplicar fórmulas comprovadas para otimizar seus processos de conformação de metal. Prepare-se para elevar seu conhecimento sobre dobragem de chapas metálicas a novos patamares!
Atualmente, as fórmulas para o cálculo da força de flexão que são amplamente utilizadas foram adotadas de fontes estrangeiras sem nenhuma informação sobre sua origem ou escopo de aplicação.
Este artigo apresenta uma análise sistemática do processo de derivação da fórmula para calcular a força de flexão, bem como os parâmetros necessários.
Além disso, uma nova abordagem para o cálculo da força de flexão é introduzida para ampliar seu escopo de aplicação.
O cálculo da força de dobra para chapas metálicas é essencial para obter processos de dobra precisos e eficientes. A compreensão desses cálculos ajuda a selecionar as ferramentas adequadas e a garantir a qualidade das dobras. Este capítulo apresenta uma visão geral dos principais conceitos, ferramentas e dicas práticas para o cálculo da força de flexão em trabalhos com chapas metálicas.
Os cálculos de força de dobra são cruciais no trabalho com chapas metálicas para garantir que a quantidade correta de força seja aplicada durante o processo de dobra. Isso evita o desperdício de material, danos à ferramenta e garante a qualidade de dobra desejada. Cálculos precisos ajudam a selecionar a prensa dobradeira e as ferramentas corretas, levando a uma produção eficiente e à redução de custos.
A força de flexão ( F ) necessária para dobrar uma chapa metálica pode ser calculada usando a fórmula:
onde:
O raio interno ( R ) da dobra é frequentemente aproximado com base na abertura da matriz ( V ):
A abertura da matriz ( V ) é selecionada com base na espessura da folha ( S ):
O comprimento mínimo do flange garante que o material não caia durante o processo de dobra e é calculado considerando a abertura da matriz e o ângulo de dobra.
Nos últimos anos, a máquina de freio de prensa ganhou uso generalizado em vários setores e expandiu seus recursos de processamento.
Apesar de sua popularidade, há uma falta de discussão sistemática sobre o cálculo da força de flexão.
Atualmente, há aproximadamente dois tipos de fórmulas de cálculo de força de flexão recomendadas pelos manuais de produtos de diferentes fabricantes. fabricantes de freios de prensa.
Na fórmula:
A fórmula recomendada pelo fabricante para calcular a força de flexão é baseada em uma fórmula mencionada anteriormente.
Ambas as fórmulas foram retiradas de vários folhetos de produtos, mas não há prova de sua exatidão.
Calculadora relacionada: Calculadora de tonelagem de prensa dobradeira
A Figura 1 é uma representação esquemática do processo de dobra de uma folha.
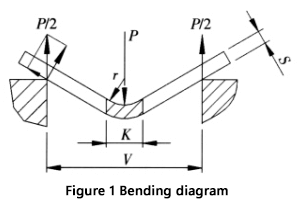
O cálculo da força de flexão e seus parâmetros são explicados a seguir:
A largura recomendada da abertura inferior da matriz (V) para flexão livre é de 8 a 10 vezes a espessura da folha (S), com uma relação largura/espessura de V/S = 9.
Os fabricantes de prensas dobradeiras fornecem os valores da largura da matriz (V) e do raio interno (r) da peça de trabalho dobrada em sua tabela de parâmetros de força de flexão. A relação entre o raio e a largura é geralmente r = (0,16 a 0,17) V e, neste caso, o valor de 0,16 é usado.
Durante o processo de flexão, o material na zona de deformação sofre uma deformação plástica significativa, fazendo com que ele se curve em torno da linha central.
Em alguns casos, pequenas rachaduras podem aparecer na superfície externa da área curva.
A tensão na zona de deformação, exceto perto da camada central, é próxima à resistência à tração do material, com a parte superior da camada neutra sendo comprimida e a parte inferior sendo tensionada.
A Figura 2 ilustra a seção transversal e o diagrama de tensão correspondente na zona de deformação.
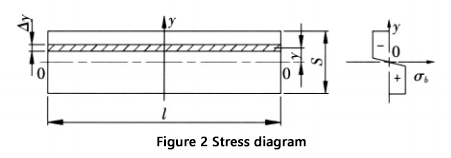
O momento de flexão na seção da zona de deformação é:
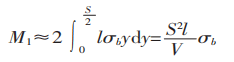
O momento de flexão produzido pela força de flexão na zona de deformação está representado na Figura 1.
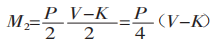
De M1 = M2, obtemos:
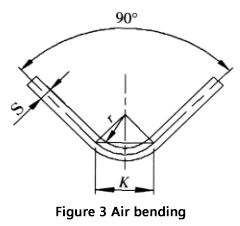
Ao dobrar uma chapa com um molde universal em uma máquina de dobra, como mostrado na Figura 3, a maioria das chapas é dobrada a 90°. Nesse caso, K é:
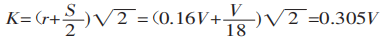
Substituindo K na equação (1), obtemos:
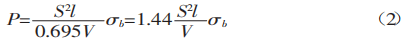
A resistência à tração de materiais comuns, σb, é de 450 N/mm². Esse valor pode ser usado na fórmula (2) para calcular o resultado.
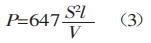
A fórmula para calcular a força de flexão obtida aqui está de acordo com as informações fornecidas em folhetos estrangeiros.
As variáveis na fórmula são:
Como pode ser visto no processo de derivação, ao usar as fórmulas (2) ou (3) para calcular a força de flexão, é importante garantir que duas condições adicionais sejam atendidas: a relação entre largura e espessura (V/S) deve ser igual a 9, e a relação entre raio e largura deve ser igual a 0,16.
Se essas condições não forem atendidas, podem ocorrer erros significativos.
O cálculo da força de flexão pode ser complicado quando não é possível atender aos dois requisitos adicionais (relação largura/espessura V/S = 9 e relação raio/largura = 0,16) devido a limitações do projeto ou do processo.
Nessas situações, é recomendável seguir estas etapas:
Essas etapas fornecerão um resultado mais preciso e confiável em comparação com o uso da fórmula comumente utilizada. Um exemplo para ilustrar esse processo é mostrado na Figura 4.
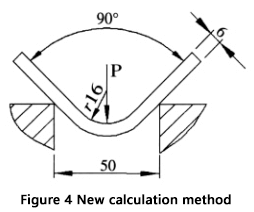
Dado: Espessura da chapa (S) = 6 mm, comprimento da chapa (l) = 4 m, raio de curvatura (r) = 16 mm, largura da abertura da matriz inferior (V) = 50 mm e resistência à tração do material (σb) = 450 N/mm².
Pergunta: Como podemos calcular a força de flexão necessária para a flexão de ar?
Aqui estão as etapas:
Primeiro, calcule a proporção entre a largura e a espessura e a proporção entre o raio e a largura:
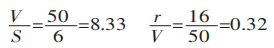
Em seguida, calcule a largura projetada da área de deformação:
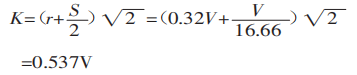
Por fim, use a fórmula (1) para calcular a força de flexão:
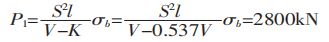
Se a fórmula normalmente recomendada for usada para calcular a força de flexão:
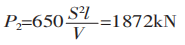
Pode-se deduzir de P1/P2 = 1,5 que a diferença entre P1 e P2 é 1,5 vezes.
O motivo dessa discrepância é que, neste exemplo, o raio de curvatura é relativamente grande, o que resulta em uma área deformada maior e, portanto, exige uma força de curvatura maior.
A proporção entre o raio e a largura nesse exemplo é de 0,32, o que supera os critérios mencionados anteriormente.
O uso da fórmula padrão para calcular a força de flexão não é adequado para esse cenário. As vantagens de usar o novo método de cálculo podem ser observadas neste exemplo.
Além disso, há uma calculadora on-line disponível para calcular a força de flexão usando o novo método.
Tabela de resistência à tração
| Material | Resistência à tração | ||
|---|---|---|---|
| Americano | Europeu | China | N/mm² |
| Alumínio 6061 | Alu50 | LD30 | 290 |
| Alumínio 5052 | Alu35 | LF2 | 303 |
| 1010 Aço macio | DC01 | 10/10F | 366 |
| A 536 -80 G 60-40-18 | GGG-40 | QT400-18 | 400 |
| A 351 G CF 8 | G-X 6CrNi 18 9 | Q235 | 450 |
| A 572 G50 | S 355 MC | Q345 | 550 |
| Aço inoxidável 304 | Inox V2A | 0Cr18Ni9 | 586 |
| Aço inoxidável 316 | Inox V4A | 0Cr17Ni12Mo2 | 600 |
| 4140 Baixa liga | 42 CrMo 4 | 42CrMo | 1000 |
As fórmulas para calcular os parâmetros de cunhagem são diferentes da dobra de ar.
1. Largura do veio da matriz:
V = chapa metálica espessura × 5
2. O raio interno é determinado pela ponta do punção, que deve ser escolhida de acordo com a fórmula a seguir:
Raio = espessura da chapa metálica × 0.43.
3. Força necessária para a cunhagem：
F(kn/m)=Espessura2×1,65×Resistência à tração (N/mm2)×4,5/Largura da matriz Vee
4. A fórmula para calcular a borda interna mínima permanece a mesma:
Borda interna mínima = Die vee × 0.67
Algumas ferramentas precisam de uma força específica para produzir a chapa metálica e gerenciar o retorno elástico a fim de obter o perfil necessário.
Como exemplo, consideraremos as ferramentas joggle, que fazem duas dobras de uma vez com uma distância curta entre a dobra e a contra-dobra.
Como essas ferramentas fazem duas dobras de uma só vez, springback deve ser completamente cancelado por meio de cunhagem.
A equação para calcular a força necessária é a seguinte:
As ferramentas de joggle geralmente consistem em um suporte de inserção no qual as ferramentas de joggle escolhidas de acordo com o joggle e o ângulo necessário são fixadas com parafusos de fixação.
É importante solicitar orientação técnica do fabricante antes da compra, pois esses sistemas só podem dobrar chapas metálicas finas, de no máximo 2 mm, mas a espessura máxima dependerá do tipo de inserção e poderá ser inferior a 2 mm.
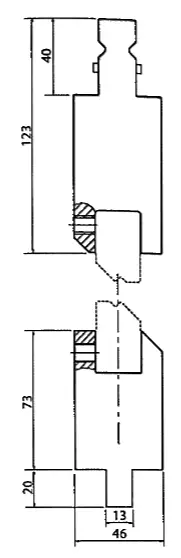
Veja abaixo as respostas para algumas perguntas frequentes:
A resistência à tração desempenha um papel fundamental na determinação da força de flexão necessária para a chapa metálica. A resistência à tração é a tensão máxima que um material pode suportar ao ser esticado antes de se romper. Quando a chapa metálica é dobrada, ela sofre tensões de tração e compressão. A superfície externa da dobra é submetida à tensão de tração, enquanto a superfície interna é submetida à tensão de compressão.
A força de flexão necessária é diretamente influenciada pela resistência à tração do material, pois uma maior resistência à tração significa que o material pode suportar uma tensão maior sem falhar. Isso implica que, para materiais com maior resistência à tração, é necessária uma força maior para atingir o mesmo grau de flexão em comparação com materiais com menor resistência à tração.
Para calcular a força de flexão, é considerada a tensão de flexão, que está relacionada à resistência à tração. A fórmula da tensão de flexão
envolve o momento de flexão (M), a distância do eixo neutro até a fibra mais externa (c) e o momento de inércia da seção transversal (I). O momento de flexão é influenciado pela força aplicada e pelo comprimento do braço de alavanca. Garantir que a tensão de flexão não exceda a resistência à tração do material é fundamental para evitar falhas durante a flexão.
Em resumo, a maior resistência à tração exige uma força de flexão maior para dobrar a chapa metálica sem causar falhas, destacando a importância de considerar as propriedades do material nos cálculos da força de flexão.
Ao calcular a força de flexão para chapas metálicas, vários fatores importantes precisam ser considerados para garantir resultados precisos e confiáveis. Os principais fatores que influenciam os cálculos da força de flexão incluem:
As propriedades do material desempenham um papel fundamental, principalmente a resistência à tração e a resistência ao escoamento. A resistência à tração é a tensão máxima que um material pode suportar antes de falhar, sendo que diferentes materiais têm resistências variadas. Por exemplo, o alumínio tem uma resistência à tração de 200 a 300 N/mm², o aço macio (Q235) varia de 370 a 500 N/mm² e o aço inoxidável tem cerca de 650 a 700 N/mm². A resistência ao escoamento determina a tensão na qual o material começa a se deformar plasticamente, sendo que uma resistência ao escoamento mais alta exige mais força de flexão.
A espessura do material afeta significativamente a força de flexão, pois materiais mais espessos resistem mais à deformação, exigindo maior força. As fórmulas de cálculo normalmente incluem a espessura do material como uma variável-chave.
O raio e o ângulo da dobra também são importantes. O raio de curvatura interno, ou o raio da curvatura, influencia a força necessária, sendo que raios menores precisam de mais força devido ao aumento da concentração de tensão. O ângulo da dobra afeta a força necessária, com a maioria dos cálculos baseados em uma dobra de 90 graus, mas exigindo ajustes para ângulos diferentes.
A configuração do ferramental e da matriz, especificamente a abertura em V da matriz inferior, afeta a força de dobra. A largura do canal inferior da matriz na máquina de dobra está relacionada à espessura do material, e a dobra de precisão pode exigir uma abertura em V mais estreita para materiais mais finos.
O fator K e a posição do eixo neutro também influenciam o processo de flexão. O fator K, embora esteja mais diretamente relacionado ao cálculo das concessões e deduções de dobra, afeta o comportamento geral da dobra e a força necessária ao determinar onde o material não é comprimido nem esticado.
Por fim, o cálculo da força de flexão normalmente envolve uma fórmula que incorpora a resistência à tração do material, a espessura e o comprimento da curva. Por exemplo, uma fórmula simplificada para aço com baixo teor de carbono é
em que ( t ) é a espessura em mm e ( l ) é o comprimento em metros, com o resultado em toneladas.
Ao considerar esses fatores, é possível calcular com precisão a força de dobra necessária para as operações de dobra de chapas metálicas, garantindo que a máquina de prensa dobradeira seja ajustada corretamente para obter a dobra desejada sem causar falha no material ou deformação excessiva.
Para determinar as configurações apropriadas para uma máquina de prensa dobradeira, é necessário considerar vários fatores-chave para garantir a dobra precisa e eficiente da chapa metálica. Primeiro, identifique o tipo e a espessura do material, pois eles influenciam significativamente a força de dobra necessária. Metais diferentes, como aço inoxidável e alumínio, têm resistência e elasticidade variadas, o que afeta a força necessária para dobrar.
Em seguida, calcule a tonelagem necessária usando a fórmula ( P=650S²L/V ), em que ( P ) é a força de dobra, ( S ) é a espessura da placa de metal e ( V ) é a abertura da matriz inferior. Leve em conta o comprimento e o ângulo da dobra, pois ângulos mais agudos exigem maior tonelagem. Garanta o suporte e o alinhamento adequados do material para evitar deflexões e imprecisões.
Diferentes métodos de dobra, como dobra a ar, dobra inferior e cunhagem, exigem diferentes tonelagens, sendo a dobra a ar a linha de base e a cunhagem exigindo cerca de oito vezes a tonelagem da dobra a ar. Verifique se a tonelagem não excede o limite de tonelagem central da prensa dobradeira para evitar sobrecarga e possíveis danos.
Selecione o ferramental adequado que corresponda ao material e aos requisitos de dobra, garantindo que o ferramental esteja devidamente alinhado e instalado. Calibre a máquina inspecionando-a e limpando-a, ajustando o backgauge e calibrando a posição e o ângulo do cilindro. Programe a prensa dobradeira de acordo com a tonelagem e os parâmetros de dobra calculados e faça um teste com material de sucata para ajustar as configurações e garantir os resultados desejados.
Seguindo essas etapas, é possível determinar com precisão as configurações apropriadas para a sua máquina de prensa dobradeira, o que resulta em operações de dobra de chapas metálicas precisas e eficientes.
As fórmulas e etapas fornecidas para o cálculo da força de flexão são adequadas não apenas para a flexão angular de uma chapa, mas também para a flexão em forma de arco (que tecnicamente deve ser chamada de flexão angular com um grande raio de flexão).
É fundamental ter em mente que a formação de uma forma de arco requer um projeto de molde exclusivo.
Ao projetar a área de deformação, o cálculo deve se basear nos parâmetros de processo estabelecidos durante o processo, que não podem ser determinados por meio de uma única fórmula.
Em uma fábrica de torres de ferro específica, dobramos com sucesso um cilindro com uma espessura de parede de 12 mm, um diâmetro de 800 mm e um comprimento de 16 m usando uma prensa de 28.000 kN máquina de freio e um molde circular.
O método descrito neste artigo foi utilizado para determinar a força de flexão e produziu resultados satisfatórios ao projetar um molde para uma forma de arco.
Leia mais:
Como fundador do MachineMFG, dediquei mais de uma década de minha carreira ao setor de metalurgia. Minha vasta experiência permitiu que eu me tornasse um especialista nas áreas de fabricação de chapas metálicas, usinagem, engenharia mecânica e máquinas-ferramentas para metais. Estou sempre pensando, lendo e escrevendo sobre esses assuntos, esforçando-me constantemente para permanecer na vanguarda do meu campo. Permita que meu conhecimento e experiência sejam um trunfo para sua empresa.
PT_BR 
EN 
AR 
DE 
ES 
FR 
ID 
IT 
JA 
NL 
PT 
RU 
KO 
TR