Você já se perguntou como os diferentes materiais afetam a dobragem de chapas metálicas? Neste artigo esclarecedor, um engenheiro mecânico experiente compartilha sua experiência sobre o impacto dos tipos de materiais, da espessura e de outros fatores nos cálculos de dobra. Descubra insights valiosos que podem ajudá-lo a otimizar seus processos de fabricação de chapas metálicas e a obter resultados precisos. Continue lendo para aprender com um especialista do setor e elevar seu conhecimento sobre dobragem ao próximo nível!
Nossa abrangente calculadora on-line de dobragem de chapas metálicas é uma ferramenta essencial para a metalurgia de precisão, permitindo que você determine com rapidez e precisão os parâmetros críticos para operações de dobragem de chapas metálicas. Essa calculadora avançada fornece informações importantes sobre:
Instruções para o uso ideal:
Aproveite essa poderosa calculadora para aprimorar seu processo de fabricação de chapas metálicas, melhorar a precisão, reduzir o desperdício de material e agilizar seu fluxo de trabalho de produção.
Leitura relacionada:
A dobra de chapas metálicas é um processo fundamental na fabricação de metais que envolve a deformação de uma chapa de metal ao longo de um eixo reto. Esse processo é essencial para a criação de uma ampla gama de produtos de metal com formas e funcionalidades variadas. Para obter curvas precisas e exatas, vários conceitos fundamentais precisam ser compreendidos e considerados durante as etapas de projeto e fabricação.
O processo de dobra começa com um projeto detalhado da peça final. Isso envolve a criação de modelos 3D usando software CAD, como o AutoCAD ou o SolidWorks. O projeto deve levar em conta vários fatores, inclusive a tolerância de dobra, os relevos e as linhas de dobra. Arquivos adequadamente preparados garantem que o produto final atenda às especificações e aos padrões de qualidade desejados.
A tolerância de dobra representa o comprimento do eixo neutro do início ao fim da dobra. O fator K é um coeficiente que ajuda a determinar a posição do eixo neutro em relação à espessura do material. Ele varia de acordo com as propriedades do material e o método de dobra utilizado. Por exemplo, em um estudo de caso envolvendo chapas metálicas de alumínio, foi usado um fator K de 0,3 para obter curvas precisas. Compreender e calcular com precisão a tolerância de dobra e o fator K é essencial para obter dobras precisas e manter as dimensões gerais da peça.
O raio da dobra é a curvatura da dobra e é vital para manter a integridade estrutural da chapa metálica. Normalmente, o raio mínimo de curvatura deve ser pelo menos igual à espessura da chapa metálica para evitar deformações ou rachaduras. A garantia de raios de curvatura consistentes em todas as curvas também pode contribuir para projetos econômicos e eficientes.
Springback é a tendência de uma peça de chapa metálica dobrada retornar parcialmente à sua forma original depois que a força de dobra é removida. Esse fenômeno pode levar a imprecisões nas dimensões finais da peça. Para compensar o retorno elástico, uma força adicional pode ser aplicada por meio de métodos como o bottoming e o coining. O bottoming comprime a chapa metálica na parte inferior da matriz, eliminando efetivamente o retorno elástico. A cunhagem envolve a aplicação de alta pressão para criar uma deformação permanente, reduzindo ainda mais os efeitos do retorno elástico.
O eixo neutro é uma linha imaginária dentro da chapa metálica que não sofre alongamento ou compressão durante a dobra. A zona de tensão está localizada na parte externa da dobra, onde o material se estica, enquanto a zona de compressão está localizada na parte interna, onde o material se comprime. Compreender essas zonas é fundamental para cálculos precisos de flexão e para prever o comportamento do material durante o processo de flexão.
A orientação da dobra refere-se à direção em que as dobras são feitas. Para uma produção econômica e eficiente, as dobras originadas do mesmo plano devem ser orientadas na mesma direção. Essa abordagem reduz a necessidade de reorientar a peça, economizando tempo e recursos. A orientação consistente das dobras também ajuda a manter as ferramentas e a configuração uniformes durante todo o processo de fabricação.
Vários métodos de dobra são empregados no setor, cada um com suas próprias vantagens e limitações:
Ao entender completamente esses conceitos-chave, os projetistas e engenheiros podem tomar decisões informadas durante o processo de dobra, garantindo peças de chapa metálica precisas e de alta qualidade.
Veja abaixo as respostas para algumas perguntas frequentes:
O fator K na flexão de chapas metálicas é um parâmetro crucial que representa a relação entre a distância do eixo neutro e a espessura do material. O eixo neutro é uma linha imaginária dentro do metal que não sofre compressão ou alongamento durante a flexão. Essa posição se desloca do ponto médio da espessura do material à medida que o metal é dobrado.
A determinação do fator K envolve medições e cálculos. Normalmente, você dobra peças de amostra do metal e mede as principais dimensões, incluindo o raio interno da dobra, a espessura do material e a margem de dobra. O fator K pode ser calculado usando a fórmula:
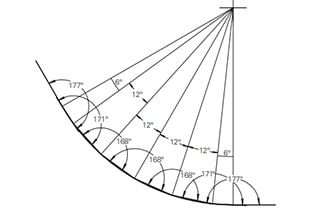
O ângulo de curvatura complementar é (180° - ângulo incluído)
Por conveniência, gráficos e tabelas de fator K são usados com frequência. Eles fornecem valores típicos com base no tipo de material, na espessura e no método de flexão. O fator K é influenciado por vários fatores, incluindo as propriedades do material, o raio de curvatura, a espessura do material e o método de curvatura usado.
Os valores do fator K geralmente variam entre 0,3 e 0,5. Por exemplo, materiais macios, como cobre macio, têm um fator K em torno de 0,35, materiais semiduros, como aço doce e alumínio, em torno de 0,41, e materiais duros, como bronze e aço laminado a frio, em torno de 0,45.
Em aplicações práticas, o fator K é essencial para o cálculo de concessões e deduções de dobras, garantindo padrões planos precisos e evitando defeitos durante o processo de dobra. Ele é usado com frequência em softwares de projeto e por freio de prensa operadores para a fabricação precisa de chapas metálicas.
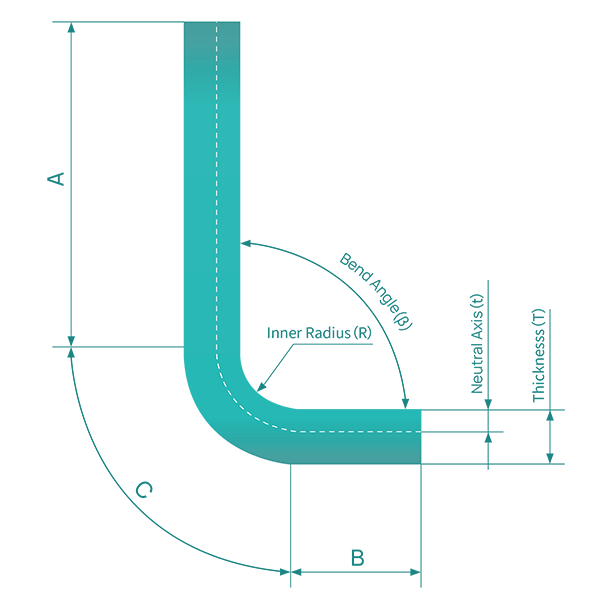
Para calcular a tolerância de dobra para chapas metálicas, você precisa considerar vários parâmetros-chave e usar uma fórmula específica. Os parâmetros de que você precisa são a espessura do material (T), o ângulo de dobra (A), o raio interno (R) e o fator K (K). A margem de curvatura (BA) é o comprimento do arco da curvatura medido ao longo do eixo neutro da chapa metálica.
A fórmula para calcular o subsídio de dobra é a seguinte:
Onde:
Por exemplo, considerando um ângulo de curvatura (A) de 120 graus, um raio interno (R) de 6,5 mm, uma espessura de material (T) de 2,5 mm e um fator K (K) de 0,5, você pode calcular a tolerância de curvatura da seguinte forma:
1. Converta o ângulo de curvatura em radianos, se necessário:
2. Aplique os valores à fórmula:
A tolerância de dobra calculada (BA) é de 16,23 mm. Esse valor é então usado para determinar o comprimento plano da chapa metálica necessária para formar a peça de trabalho desejada. O comprimento plano pode ser calculado adicionando-se os comprimentos das pernas à tolerância de dobra. Isso garante a fabricação precisa e eficiente de peças de chapa metálica.
A tolerância de dobra (BA) e a dedução de dobra (BD) são dois conceitos essenciais na dobra de chapas metálicas que têm finalidades diferentes no processo de fabricação. A tolerância de dobra refere-se ao comprimento do material necessário para criar uma dobra, medido ao longo do eixo neutro da chapa metálica. Ela é responsável pelo material real usado na dobra e é adicionada ao comprimento plano para garantir que as dimensões finais da peça de trabalho atendam às especificações do projeto.
Por outro lado, a dedução de dobra representa a quantidade de material que deve ser subtraída do comprimento total do plano para obter a dobra desejada. Essa dedução é necessária para compensar o efeito de retorno elástico que ocorre quando a força de dobra é removida, garantindo que o ângulo de dobra final seja preciso e que as dimensões da peça sejam mantidas.
Em resumo, enquanto a tolerância de dobra é adicionada ao comprimento plano para o uso adequado do material durante a dobra, a dedução de dobra é subtraída para levar em conta o comportamento do material após a dobra, especialmente a tendência de se desdobrar ligeiramente. Ambos os cálculos são essenciais para obter componentes de chapa metálica precisos e exatos.
O cálculo preciso do comprimento plano na dobra de chapas metálicas é crucial por vários motivos que afetam diretamente a qualidade, a eficiência e a relação custo-benefício do processo de fabricação.
Primeiro, os cálculos precisos do comprimento plano garantem que as dimensões da peça final correspondam às especificações do projeto. Ao contabilizar corretamente a tolerância e a dedução de dobras, as dimensões da peça acabada serão precisas, garantindo que ela se encaixe adequadamente na montagem geral e atenda aos requisitos de projeto pretendidos.
Em segundo lugar, cálculos precisos de comprimento plano otimizam a utilização e a eficiência do material. Ao determinar o tamanho exato da chapa metálica necessária antes da dobra, os fabricantes podem minimizar o desperdício e controlar os custos, tornando o processo de fabricação mais eficiente em termos de recursos.
Terceiro, garantir o comprimento plano correto é vital para o ajuste e a montagem adequados das peças. Dimensões incorretas podem fazer com que as peças não se encaixem como previsto, causando problemas de montagem e possível retrabalho, o que pode ser caro e demorado.
Quarto, cálculos precisos ajudam a manter a distribuição de tensão e a integridade estrutural das peças dobradas. A contabilização adequada da tolerância e da dedução de dobra garante que as peças sejam dobradas de forma a manter sua resistência e durabilidade, o que é essencial para a confiabilidade do produto final.
Em quinto lugar, a consistência na fabricação é obtida por meio de cálculos precisos do comprimento do plano. Essa consistência reduz os erros e o retrabalho, levando a um processo de fabricação mais eficiente e confiável. Ela também garante que cada peça produzida atenda aos mesmos altos padrões.
Em sexto lugar, cálculos precisos compensam o efeito de retorno elástico do material, em que a peça dobrada tende a se desdobrar parcialmente depois que a força de dobra é removida. Ao incorporar a dedução de dobra correta, os fabricantes podem obter o ângulo de dobra desejado e manter a precisão dimensional após o processo de dobra.
Por fim, saber as dimensões exatas necessárias para o padrão plano simplifica o processo de fabricação. Isso permite operações otimizadas, facilitando a produção de componentes dobrados de alta qualidade com o mínimo de esforço e erro.
Em resumo, calcular com precisão o comprimento plano na dobra de chapas metálicas é essencial para garantir dimensões precisas, otimizar o uso de materiais, obter ajuste e montagem adequados, manter a integridade estrutural, garantir a consistência na fabricação, compensar o retorno elástico e simplificar o processo de fabricação.
Nos cálculos de dobra de chapas metálicas, o impacto de diferentes tipos de materiais sobre o fator de dobra é significativo e multifacetado, influenciando a precisão, a qualidade e a eficiência do processo de dobra. As principais áreas afetadas incluem:
Propriedades do material:
Diferentes materiais apresentam propriedades mecânicas variadas, como resistência ao escoamento, resistência à tração e módulo de elasticidade. Essas propriedades influenciam diretamente o comportamento do material durante a flexão, afetando o fenômeno de retorno da mola e a força de flexão necessária. Por exemplo, os aços de alta resistência normalmente exigem um fator de flexão maior em comparação com os aços macios devido à sua maior resistência à deformação plástica.
Estrutura de grãos e anisotropia:
A estrutura cristalina e a orientação dos grãos dos metais desempenham um papel fundamental no comportamento de flexão. Materiais com uma estrutura de grão pronunciada, como certas ligas de alumínio, podem apresentar propriedades anisotrópicas, levando a diferentes fatores de flexão, dependendo da direção da flexão em relação à orientação do grão. Isso pode resultar em um retorno de mola inconsistente e possíveis defeitos se não for devidamente considerado nos cálculos.
Características de endurecimento por trabalho:
Os materiais com diferentes taxas de endurecimento por trabalho, como os aços inoxidáveis austeníticos e os aços de baixo carbono, exigem abordagens distintas para os cálculos do fator de flexão. O endurecimento por trabalho durante o processo de flexão pode alterar significativamente as propriedades do material, afetando a forma final e a precisão dimensional.
Coeficientes de expansão térmica:
Para processos que envolvem calor, como dobra a quente ou tratamento térmico subsequente, o coeficiente de expansão térmica do material torna-se um fator crítico. Os materiais com coeficientes mais altos podem exigir uma compensação no fator de flexão para levar em conta as alterações dimensionais durante o resfriamento.
Condição da superfície e tratamentos:
Os tratamentos de superfície, como anodização, galvanização ou endurecimento, podem alterar as propriedades da superfície do material, afetando o atrito durante a flexão e, possivelmente, alterando o fator de flexão necessário. A presença de camadas de óxido ou revestimentos deve ser considerada em cálculos precisos de flexão.
Variações de espessura:
Embora a espessura do material em si seja um fator fundamental, a consistência da espessura em toda a chapa é igualmente importante. Materiais propensos a variações de espessura, como certas ligas laminadas, podem exigir fatores de dobra adaptáveis ou cálculos mais conservadores para garantir resultados consistentes em toda a peça de trabalho.
Sensibilidade à taxa de deformação:
Alguns materiais, especialmente certas ligas de alumínio e aços de alta resistência, apresentam sensibilidade à taxa de deformação. Isso significa que o fator de flexão pode precisar ser ajustado com base na velocidade da operação de flexão, sendo que a flexão mais rápida pode exigir cálculos diferentes dos processos mais lentos e controlados.
Estado de tensão residual:
A presença de tensões residuais no material, que pode variar de acordo com o tipo de material e o histórico de processamento anterior, pode afetar significativamente o comportamento de flexão. Materiais com altos níveis de tensão residual podem exigir tratamentos de alívio de tensão ou fatores de flexão ajustados para obter resultados precisos.
Para otimizar as operações de dobra para diferentes tipos de materiais, é fundamental:
Ao considerar cuidadosamente esses impactos específicos do material sobre o fator de dobra, os fabricantes podem obter maior precisão, reduzir as taxas de refugo e otimizar seus processos de dobra de chapas metálicas em uma ampla variedade de materiais.
Como fundador do MachineMFG, dediquei mais de uma década de minha carreira ao setor de metalurgia. Minha vasta experiência permitiu que eu me tornasse um especialista nas áreas de fabricação de chapas metálicas, usinagem, engenharia mecânica e máquinas-ferramentas para metais. Estou sempre pensando, lendo e escrevendo sobre esses assuntos, esforçando-me constantemente para permanecer na vanguarda do meu campo. Permita que meu conhecimento e experiência sejam um trunfo para sua empresa.
PT_BR 
EN 
AR 
DE 
ES 
FR 
ID 
IT 
JA 
NL 
PT 
RU 
KO 
TR