Você já se perguntou como a precisão e a eficiência se unem no corte industrial? Este artigo explora o fascinante mundo das tesouras guilhotinas, detalhando suas vantagens e desafios. Saiba como a análise e a otimização mecânica podem melhorar o desempenho, garantindo que você fique à frente no campo da engenharia mecânica.
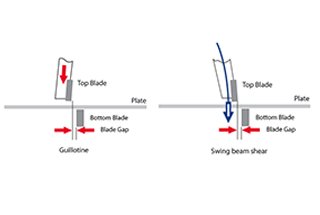
A guilhotina oferece maior eficiência, precisão e confiabilidade em comparação com a guilhotina de viga oscilante, pois elimina a folga na estrutura e permite o ajuste do ângulo de corte.
No entanto, ao cortar chapas largas e pesadas ou chapas finas de alta resistência, a guilhotina pode enfrentar desafios como a deformação da máquina, que afeta a precisão do corte.
A maioria das pesquisas nesse campo se concentra no impacto dos parâmetros de cisalhamento na precisão, no projeto e na automação do sistema de controle ou na simulação do processo de cisalhamento usando pontos discretos.
No entanto, há poucas pesquisas sobre a análise da propriedade mecânica e a otimização da estrutura das tesouras guilhotinas.
O objetivo deste artigo é abordar essa lacuna por meio da análise das características estáticas e dinâmicas da máquina-ferramenta e da simulação do processo de cisalhamento de chapas. Por meio dessa análise, são obtidos dados de cisalhamento contínuo e é proposto um esquema de otimização.
Um modelo estrutural de um NC 6 x 3200 tesoura guilhotina é mostrado na Figura 1. Durante a operação, o dispositivo de batente traseiro, acionado pelo parafuso do rolo, ajusta o comprimento de corte. O cilindro de prensagem é então comprimido pela placa de corte.
Depois que os parâmetros de corte, como a folga da lâmina e o ângulo de cisalhamento, são definidos, os cilindros hidráulicos em ambas as extremidades acionam as lâminas superior e inferior para mover e concluir o corte. corte de chapas processo.
Na análise de simulação, o filete de transição e o furo roscado são desconsiderados, e um modelo tridimensional simplificado é importado para um software de análise de elementos finitos. Os dois lados do suporte superior da ferramenta são fixados com restrições e o contato de ligação é estabelecido para simular a soldagem e a fixação da rosca das peças do suporte superior da ferramenta.
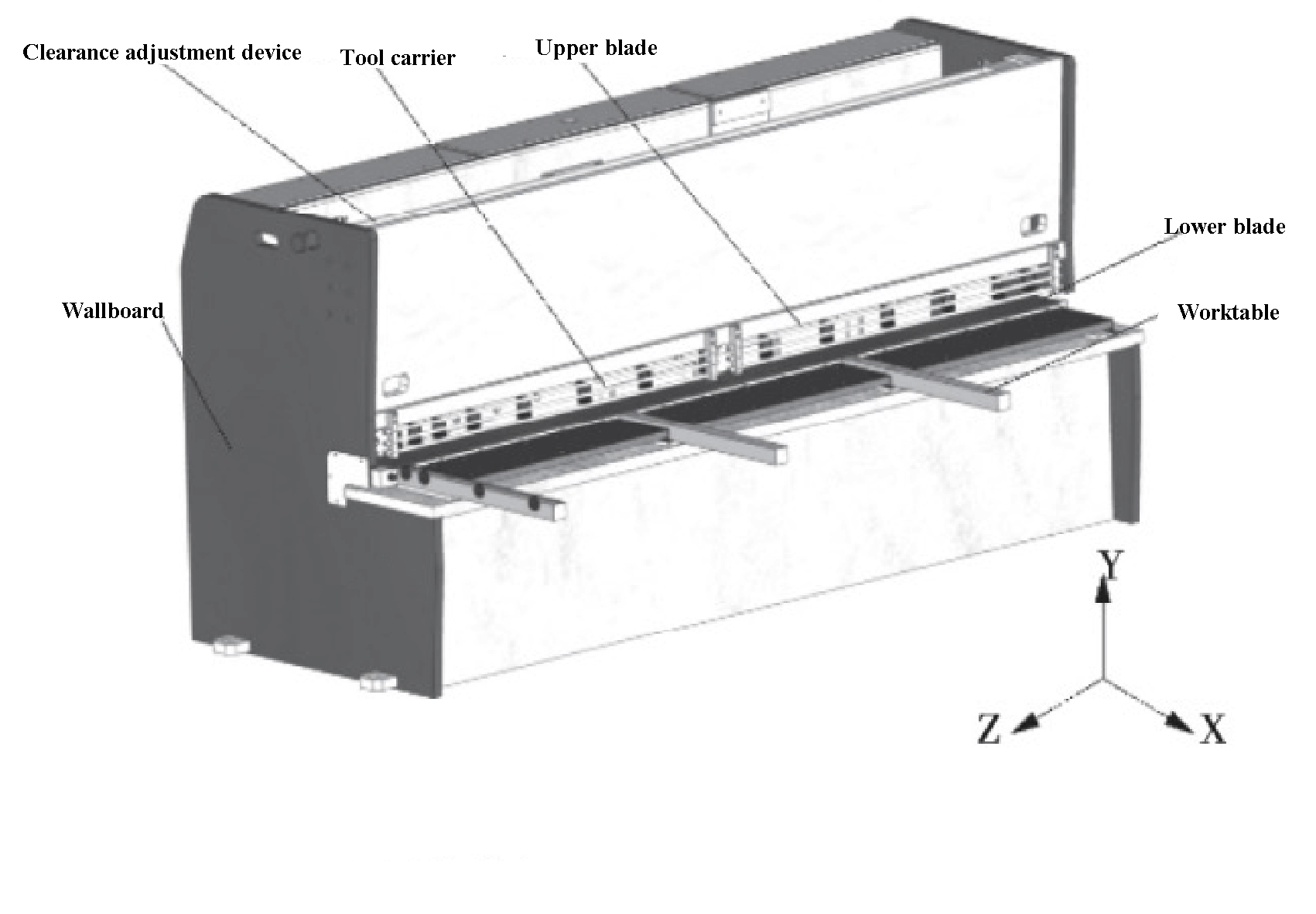
Fig. 1 Modelo estrutural da guilhotina de corte 6 × 3200 NC
De acordo com a fórmula de Norsali:

Na fórmula:
A força de cisalhamento vertical (P1) é calculada como 212,8 kN usando a fórmula (1), enquanto a força de cisalhamento horizontal (P2) é estimada como 30% da força de cisalhamento vertical, ou 63,8 kN. As forças de cisalhamento vertical e horizontal são aplicadas à torre superior e resolvidas usando o ANSYS Workbench.
A deformação em cada direção no início, no meio e no final do cisalhamento é comparada e analisada. Como visto na Tabela 1, a deformação do carro superior na direção Y é a maior, e a deformação nas direções X e Z pode ser considerada insignificante em comparação.
As posições inicial e final da deformação na direção Y são aproximadamente iguais e muito menores do que a posição intermediária. Durante o processo de cisalhamento, a deformação do porta-ferramenta superior apresenta uma tendência côncava.
Tabela 1 Tensão equivalente máxima e deformação máxima nas direções X, Y e Z do porta-ferramenta superior
| Posição de cisalhamento | Tensão máxima equivalente /MPa | Deformação máxima na direção X /mm | Deformação máxima na direção Y /mm | Deformação máxima na direção Z /mm |
| Início | 137.7 | 0.020 | 0.141 | 0.074 |
| Médio | 135.3 | 0.090 | 0.183 | 0.650 |
| Fim | 137.2 | 0.013 | 0.151 | 0.085 |
As Figuras 2 e 3 mostram a tensão equivalente máxima no meio e a deformação máxima na direção Y, respectivamente.

Fig. 2 Tensão equivalente máxima do suporte superior da ferramenta
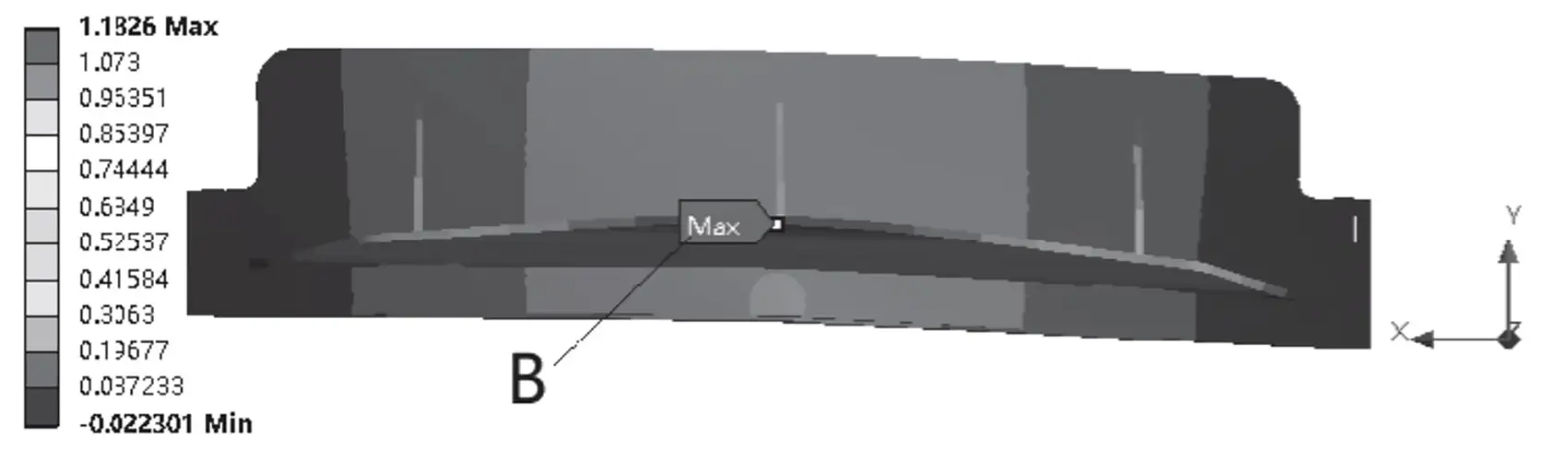
Fig. 3 Deformação máxima do porta-ferramentas superior na direção Y
Analisando a Tabela 1 e as Figuras 2 e 3, é possível determinar que a tensão equivalente do porta-ferramentas superior é a mais alta no início do processo de cisalhamento. Essa tensão está localizada na posição do cilindro hidráulico e tem um valor de 137,7 MPa, que é menor do que a tensão equivalente do suporte superior da ferramenta. resistência ao escoamento de 235 MPa para o descanso de ferramenta superior.
No meio do processo de cisalhamento, a deformação máxima do porta-ferramenta superior na direção Y é observada na placa de suporte traseiro B, com um tamanho de 1,183 mm. Enquanto isso, a deformação da lâmina na direção Y é de 0,346 mm, ou seja, menos de 1 mm e atende aos requisitos necessários.
Na simulação dinâmica, um controle deslizante é colocado na posição inicial da lâmina superior e é constantemente submetido à força de cisalhamento com uma velocidade especificada. O movimento do controle deslizante é usado para simular o processo de cisalhamento da placa.
Como a barra deslizante transmite apenas força de cisalhamento, ela foi configurada para ter contato sem atrito com a lâmina superior. Durante o corte do chapa metálicaNa Figura 4, o contato entre a lâmina superior e a chapa metálica a ser cortada é ilustrado. O comprimento de contato (s) é de 8:1.

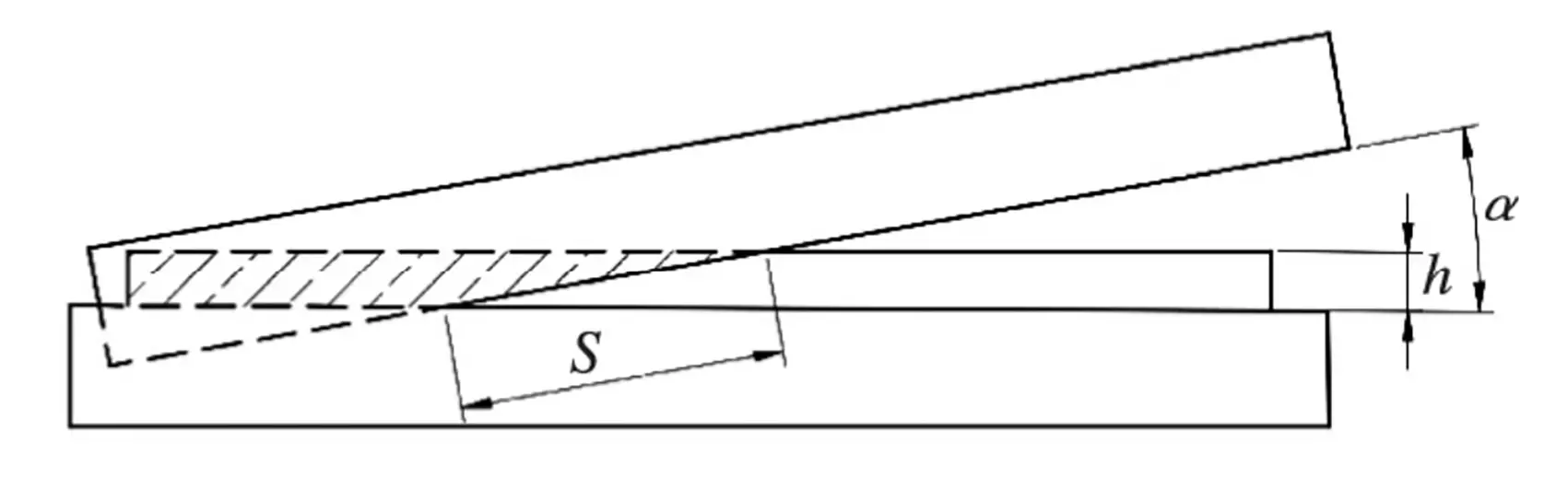
Fig. 4 Diagrama de corte
Para simplificar o cálculo, supõe-se que a força de cisalhamento seja distribuída uniformemente em uma área retangular com o comprimento (s) e a largura (t) da lâmina. Como resultado, o controle deslizante é modelado como um cuboide com o mesmo comprimento (s) e largura (t), conforme ilustrado na Figura 5.

Fig. 5 Diagrama esquemático da simulação do controle deslizante
Ao resolver a tensão equivalente máxima e a deformação máxima nas direções Y e Z em cada posição, os resultados são apresentados na Tabela 2. A tendência da deformação e da tensão do suporte superior da ferramenta durante o processo de cisalhamento é mostrada na Figura 6.
Tabela 2 Tensão equivalente máxima e deformação máxima nas direções Y e Z do porta-ferramentas superior em cada etapa de carga
| Etapa de carga | Tensão máxima equivalente /MPa | Deformação máxima na direção Y /mm | Deformação máxima na direção Z /mm |
| 1 | 138.1 | 0.265 | 0.181 |
| 2 | 153.2 | 0.380 | 0.330 |
| 3 | 158.4 | 0.403 | 0.386 |
| 4 | 159.2 | 0.469 | 0.426 |
| 5 | 157.5 | 0.592 | 0.463 |
| 6 | 153.8 | 0.571 | 0.454 |
| 7 | 148.1 | 0.580 | 0.461 |
| 8 | 150.3 | 0.635 | 0.478 |
| 9 | 153.7 | 0.543 | 0.458 |
| 10 | 154.9 | 0.477 | 0.446 |
| 11 | 153.2 | 0.482 | 0.425 |
| 12 | 141.8 | 0.358 | 0.336 |
| 13 | 136.4 | 0.250 | 0.175 |
Conforme observado na Tabela 2 e na Figura 6, a deformação do porta-ferramenta superior muda com a alteração da posição de cisalhamento. A deformação é significativa no meio e relativamente pequena e simétrica em ambos os lados, alinhando-se com os resultados da simulação estática.
A deformação máxima do porta-ferramenta superior nas direções Y e Z ocorre na etapa de carga 8, com valores de 0,635 mm e 0,478 mm, respectivamente, que são inferiores a 1 mm.
A tensão equivalente máxima é encontrada na etapa de carga 4 e tem um valor de 159,2 MPa, que é menor do que a resistência ao escoamento de 235 MPa para o porta-ferramenta superior.
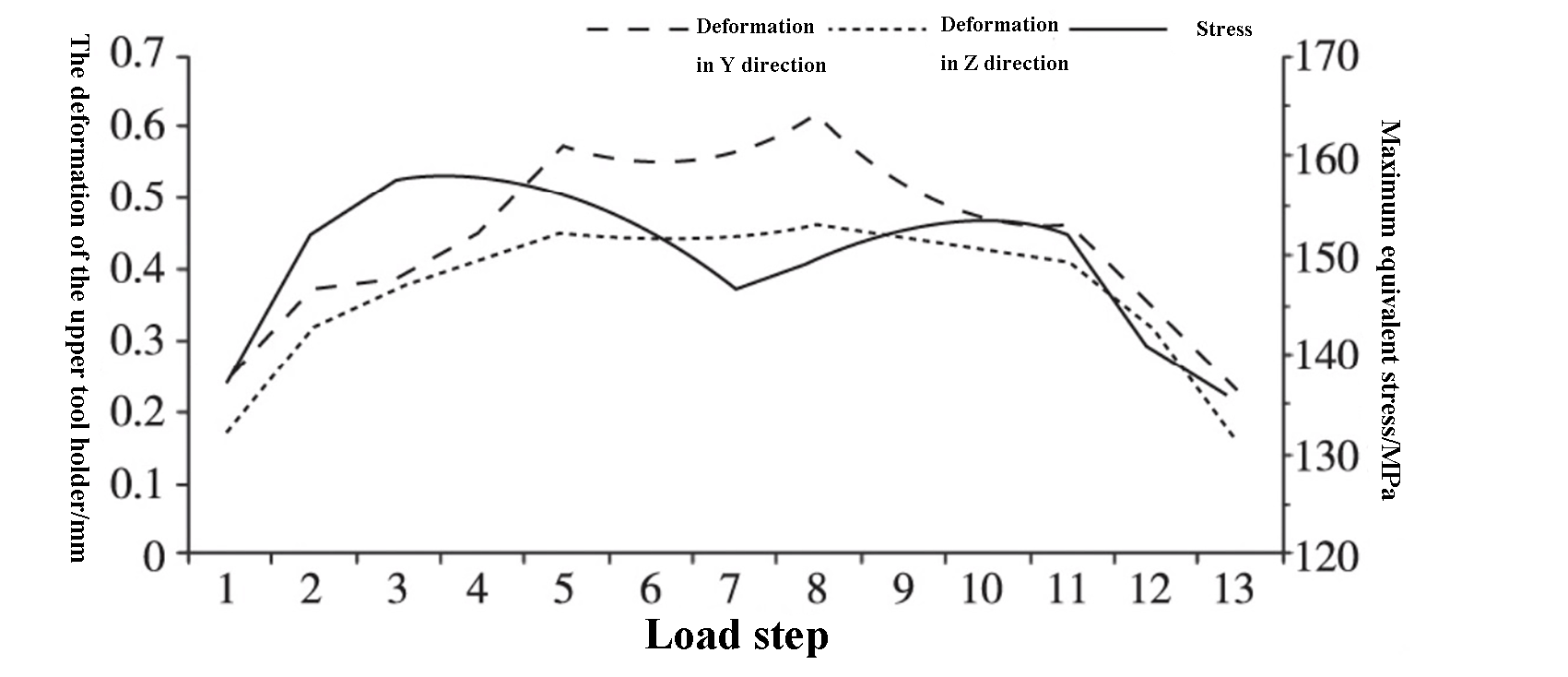
Fig. 6 Deformação e tensão equivalente máxima do suporte superior da ferramenta nas direções Y e Z
As Figuras 7, 8 e 9 mostram a deformação máxima e a tensão equivalente máxima nas direções Y e Z, respectivamente.

Fig. 7 Deformação máxima do porta-ferramentas superior na direção Y

Fig. 8 Deformação máxima do porta-ferramentas superior na direção Z

Fig. 9 Tensão equivalente máxima do suporte superior da ferramenta
Nas Figuras 7, 8 e 9, é possível observar que a deformação máxima do carro superior na direção Y ocorre na lâmina C, enquanto a deformação máxima na direção Z ocorre na lâmina D. Ambas as deformações são inferiores a 1 mm, atendendo aos requisitos do projeto.
A tensão equivalente máxima ocorre na posição E do suporte superior da ferramenta sob a influência do cilindro hidráulico. A tensão na lâmina é mínima e demonstra boa rigidez.
Na análise modal, as quatro bases da estrutura são fixas e mantidas no lugar com restrições. O método Block Lanczos é selecionado como o método de extração de modo e o número de modos expandidos é definido como 4 para resolver as quatro primeiras frequências naturais da estrutura do quadro.
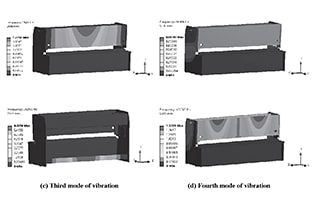
Os quatro modos de vibração são mostrados na Figura 10, e a Tabela 3 exibe as frequências naturais, as amplitudes e as formas modais dos quatro modos estruturais de vibração.
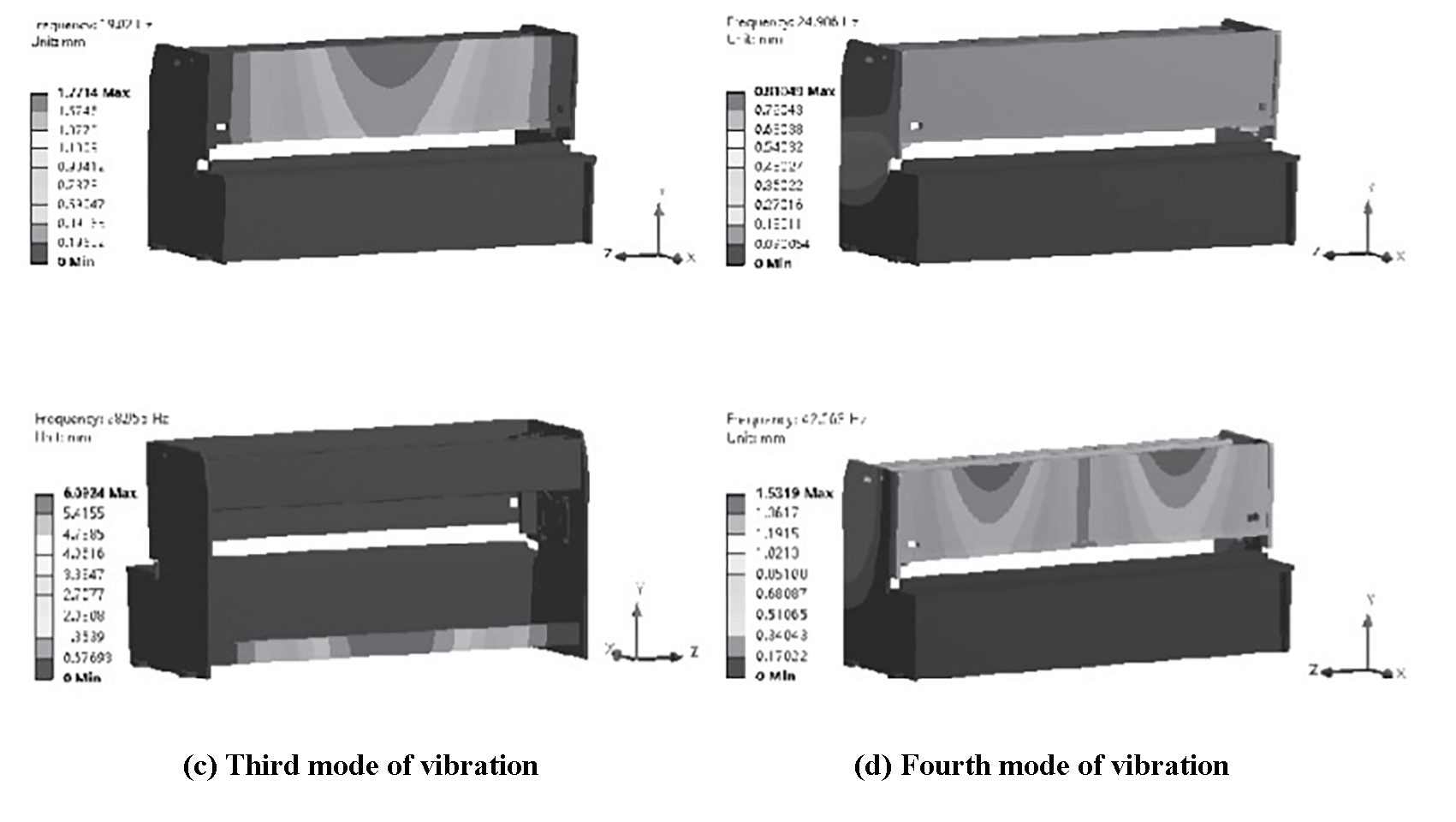
Fig. 10 Os quatro modos de vibração
Tabela 3 Tabela de dados de análise modal de cisalhamento de placas
| Pedido | Frequência /Hz | Amplitudes /mm | Modo de vibração |
| 1 | 19.02 | 1.77 | O painel frontal é dobrado para frente na direção X |
| 2 | 24.98 | 0.81 | A parte superior da estrutura se dobra e oscila na direção Z |
| 3 | 28.96 | 6.09 | A viga de suporte inferior é dobrada para frente ao longo da direção X |
| 4 | 42.66 | 1.53 | O painel frontal é dobrado para frente e para trás na direção X |
Com base na Figura 10 e na Tabela 3, pode-se observar que a deformação por vibração da estrutura afeta principalmente o painel frontal e a viga de suporte inferior, causando vibração e ruído significativos. Quando a frequência é de 19,02 Hz, a amplitude do painel frontal é maior, o que pode afetar negativamente o processo de corte e diminuir sua precisão.
No entanto, a frequência de corte da guilhotina NC é de 9 vezes por minuto, o que é significativamente menor do que a frequência natural de primeira ordem e atende aos requisitos de operação normal.
É importante minimizar a influência de fontes externas de vibração durante o processo de trabalho para evitar a deformação por vibração excessiva.
A análise das características estáticas e dinâmicas do processo de cisalhamento revela que a deformação da torre superior apresenta uma tendência côncava durante o cisalhamento, o que pode afetar a rebarba e a precisão dimensional do corte e reduzir a qualidade geral do cisalhamento.
Para melhorar a qualidade do corte, a folga da lâmina nos parâmetros de corte pode ser ajustada para aumentar a rigidez de posicionamento do suporte superior da ferramenta. Neste artigo, foi projetado um dispositivo de ajuste da folga da lâmina do tipo guia chanfrada dinâmica, conforme mostrado na Figura 11.

Fig. 11 Diagrama da estrutura da tesoura guilhotina de trilho-guia inclinado