Você já se perguntou como os projetistas de chapas metálicas garantem a precisão de seus projetos? Nesta postagem do blog, mergulharemos no fascinante mundo do design de chapas metálicas e exploraremos dois conceitos essenciais: tolerância de dobra e dedução de dobra. Também apresentaremos o fator K e sua função nos cálculos. Junte-se a nós para desvendarmos esses tópicos e fornecermos informações valiosas de especialistas do setor.
No campo do design de chapas metálicas, termos como tolerância de dobra, dedução de dobra e fator K são conceitos cruciais que afetam significativamente a precisão e a eficiência dos processos de fabricação. Esses parâmetros desempenham um papel fundamental na determinação das dimensões finais das peças de chapa metálica dobradas e na garantia de uma fabricação precisa. Vamos nos aprofundar nesses conceitos e explorar seus métodos de cálculo.
Os engenheiros e fabricantes envolvidos na fabricação de chapas metálicas utilizam algoritmos sofisticados para calcular com precisão as dimensões do padrão plano das peças, garantindo geometrias finais precisas após as operações de dobra e conformação.
O tradicional "método pinch" continua sendo uma abordagem empírica amplamente utilizada, incorporando fatores como propriedades do material, raio de curvatura, ângulo de curvatura, configurações de ferramentas e velocidades de formação. Esse método, embora eficaz, depende muito da experiência do operador e pode estar sujeito a inconsistências.
Com o advento de ferramentas computacionais avançadas, o projeto auxiliado por computador (CAD) e a análise de elementos finitos (FEA) revolucionaram a precisão e a eficiência do projeto de chapas metálicas. Essas tecnologias permitem a simulação precisa do comportamento do material durante os processos de conformação, levando em conta fenômenos complexos, como retorno elástico, tensões residuais e endurecimento por deformação.
Os sistemas CAD modernos empregam algoritmos avançados de compensação de curvatura que integram modelos teóricos com dados empíricos. Esses algoritmos normalmente utilizam uma das duas abordagens principais:
As principais plataformas de CAD, como SolidWorks, Autodesk Inventor e Siemens NX, oferecem módulos robustos de projeto de chapas metálicas com tabelas de dobras e bibliotecas de materiais personalizáveis. Esses sistemas permitem a integração de dados de dobra específicos da oficina, garantindo o alinhamento entre os projetos digitais e os processos reais de fabricação.
Além disso, tecnologias emergentes, como aprendizado de máquina e inteligência artificial, estão sendo aplicadas para otimizar os cálculos de curvatura, aproveitando vastos conjuntos de dados históricos de produção para refinar as previsões e se adaptar a combinações exclusivas de materiais e ferramentas.
Para aumentar a compreensão dos leitores sobre os conceitos básicos de projeto de chapas metálicas cálculo, os seguintes pontos serão resumidos e explicados:
Para uma compreensão mais clara de tolerância a dobrasConsulte a Figura 1, que ilustra uma única dobra em um componente de chapa metálica. A Figura 2 mostra a peça em seu estado desdobrado.
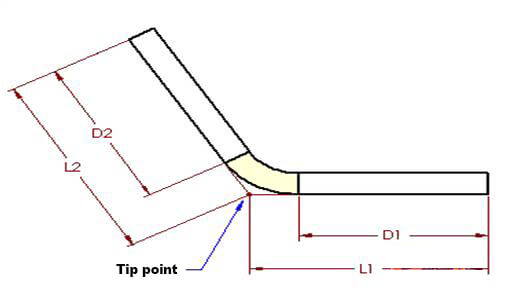
Figura 1
Figura 2
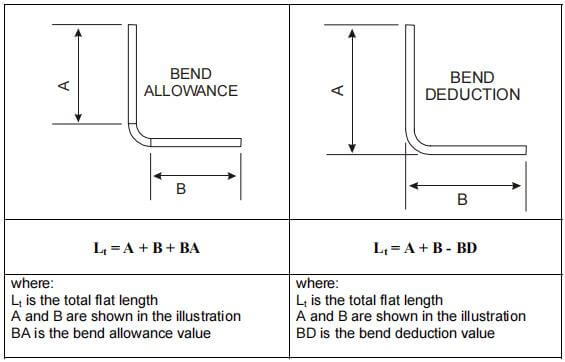
O algoritmo de tolerância de dobra descreve o comprimento desdobrado (LT) de uma peça de chapa metálica como a soma dos comprimentos de cada segmento depois que a peça é achatada, mais o comprimento da área de dobra achatada.
O tolerância a dobras (BA) representa o comprimento da área de dobra achatada. Assim, o comprimento total da peça pode ser expresso pela equação (1):
LT = D1 + D2 + BA (1)
A área de flexão (ilustrada em amarelo claro na ilustração) é a área que teoricamente sofre deformação durante o processo de flexão.
Para determinar a geometria da peça desdobrada, siga estas etapas:
A tarefa de determinar o comprimento da área de flexão achatada, representada por BA na figura, é um pouco mais desafiadora.
O valor de BA varia de acordo com fatores como tipo de material e espessura do material, raio de curvatura e ângulo, bem como o processo de dobra, o tipo de máquina e a velocidade da máquina.
O valor de BA pode ser obtido de várias fontes, incluindo fornecedores de materiais de chapa metálica, dados experimentais, experiência e manuais de engenharia.
No SolidWorks, é possível inserir diretamente os valores de BA ou usar o fator K (que será discutido posteriormente) para calcular os valores.
O mesa de dobra é a maneira mais precisa de especificar diferentes tolerâncias de flexão para diferentes situações com diferentes espessuras, raios e ângulos.
A criação da mesa de dobra inicial pode levar algum tempo, mas, uma vez formada, partes dela podem ser reutilizadas no futuro.
Podem ser inseridas informações iguais ou diferentes para cada dobra da peça.
1) Padrões para curvatura comum
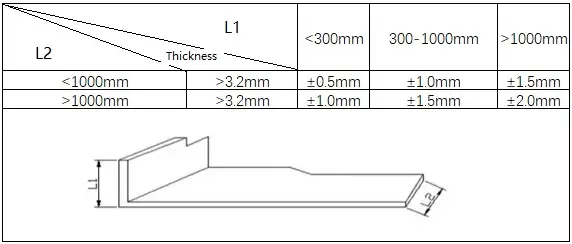
2) Padrões para dobragem em Z
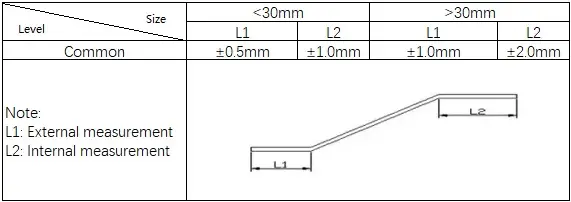
3) Padrões para curvatura em V
4) Padrões para Dobra em U
Leitura relacionada: Calculadora de força de curvatura em forma de V e U
Dedução de dobra é um termo usado para descrever a quantidade de retrocesso no processo de dobragem de chapas metálicas. Esse é outro algoritmo simples para descrever o processo.
As Figuras 1 e 2 também se aplicam a esse conceito. De acordo com o método de dedução de flexão, o comprimento achatado (LT) da peça é igual à soma dos comprimentos das duas seções planas que se estendem até o "ponto de ponta" (a interseção hipotética das duas seções planas), menos a dedução de flexão (BD).
Assim, o comprimento total da peça pode ser expresso conforme mostrado na equação (2):
LT = L1 + L2 - BD (2)
O valor da BD pode ser determinado ou obtido de várias fontes, como a planilha material metálico fornecedores, dados experimentais, experiência, manuais de engenharia com equações ou tabelas, etc.
Figura 3
É importante que os usuários familiarizados com o método de dedução de flexão entendam a relação com o método de permissão de flexão, que é comumente adotado no SolidWorks.
A relação entre os dois valores pode ser facilmente deduzida usando as duas geometrias de flexão e desdobramento de peças.
Ao comparar as equações (1) e (2), temos:
LT = D1 + D2 + BA (1) LT = L1 + L2 - BD (2)
E, portanto,
D1 + D2 + BA = L1 + L2 - BD (3)
Na Figura 3, o ângulo A representa o ângulo de flexãoque descreve o ângulo varrido pela peça durante a flexão e também o ângulo do arco formado pela área de flexão, que é mostrado em duas metades.
Usando as dimensões e os princípios dos triângulos retângulos, podemos derivar as seguintes equações:
D1 = L1 - (R + T)TAN(A/2) (4) D2 = L2 - (R + T)TAN(A/2) (5)
Substituindo as equações (4) e (5) na equação (3), podemos obter a relação entre BA e BD:
BA = 2(R + T)TAN(A/2) - BD (6)
E quando o ângulo de flexão é de 90 graus, essa equação se simplifica para:
BA = 2(R + T) - BD (7)
Essas equações (6) e (7) fornecem um método conveniente para a conversão de um algoritmo para outro, usando apenas a espessura do material, o ângulo/raio de curvatura etc. como parâmetros.
Para os usuários do SolidWorks, essas equações fornecem um método direto para converter a dedução de dobra em tolerância de dobra.
O valor da tolerância de dobra pode ser usado para toda a peça ou para cada dobra individual, ou pode ser incluído em uma tabela de dados de dobra.
O fator K é um valor autônomo que explica a flexão e o desdobramento da chapa metálica em vários cenários geométricos.
É também um valor autônomo usado para calcular a tolerância à flexão (BA) sob várias condições, como diferentes espessuras de material, ângulos de flexão e raios.
As Figuras 4 e 5 são fornecidas para ajudar a esclarecer a definição detalhada do fator K.
Figura 4
Figura 5
Podemos confirmar que há um eixo neutro na espessura da peça de chapa metálica. A chapa material metálico nesse eixo neutro na região de flexão não é esticado nem comprimido, o que significa que é a única área que não se deforma durante a flexão.
As Figuras 4 e 5 mostram o limite entre as regiões rosa e azul.
Durante a flexão, a região rosa se comprime e a região azul se estende. Se a camada neutra da chapa metálica não for deformada, o comprimento de seu arco na região de flexão permanecerá o mesmo, quer a peça seja dobrada ou achatada.
Como resultado, a margem de flexão (BA) deve ser igual ao comprimento do arco da camada neutra na região de flexão da peça de chapa metálica, que é mostrada em verde na Figura 4.
A posição da camada neutra da chapa metálica depende das propriedades de um material específico, como a ductilidade.
Supõe-se que a distância entre a camada de chapa metálica neutra e a superfície seja "t", ou seja, a profundidade da superfície da peça de chapa metálica para dentro do material na direção da espessura.
Como resultado, o raio do arco da camada neutra pode ser expresso como (R + t). Usando essa expressão e o ângulo de flexão, o comprimento do arco da camada neutra (BA) pode ser calculado.
BA = Pi(R+T)A/180
Para simplificar a definição da camada neutra da chapa metálica e torná-la aplicável a todos os materiais, foi introduzido o conceito do fator K.
A definição do fator K é: é a relação entre a espessura da camada neutra da chapa metálica e a espessura total do material da peça de chapa metálica. Em outras palavras, o fator K é definido como:
K = t/T
Portanto, o valor de K sempre estará dentro do intervalo de 0 a 1. Se o fator K for 0,25, isso indica que a camada neutra está situada a 25% da espessura total do material da chapa metálica.
Da mesma forma, se for 0,5, significa que a camada neutra está localizada a 50% de toda a espessura, e assim por diante.
Ao combinar as equações mencionadas acima, é possível obter a seguinte equação (8):
BA = Pi(R+K*T)A/180 (8)
Portanto, o valor de K sempre estará entre 0 e 1.
Se o fator K for 0,25, isso significa que a camada neutra está localizada a 25% da espessura do material da chapa metálica da peça.
Da mesma forma, se for 0,5, significa que a camada neutra está localizada a 50% de toda a espessura, e assim por diante.
A origem do fator K pode ser rastreada até fontes tradicionais, como fornecedores de materiais de chapa metálica, dados de teste, experiência, manuais etc.
Entretanto, em alguns casos, o valor fornecido pode não ser expresso como um fator K claro, mas ainda é possível encontrar a relação entre eles.
Por exemplo, se um manual ou literatura descreve o eixo neutro como "posicionado a 0,445x a espessura do material a partir da superfície da chapa metálica", isso pode ser interpretado como um fator K de 0,445, ou seja, k = 0,445.
Quando esse valor de K é substituído na equação (8), a seguinte fórmula pode ser obtida.
BA = A (0,01745R + 0,00778T)
Se a equação (8) for modificada por outro método, a constante na equação (8) for calculada e todas as variáveis forem mantidas, será possível obter o seguinte:
BA = A (0,01745 R + 0,01745 K*T)
Ao comparar as duas equações, é fácil determinar que 0,01745 * k = 0,00778 e, portanto, k pode ser calculado como 0,445.
Descobriu-se que o sistema SolidWorks também fornece um algoritmo de tolerância à flexão para materiais específicos quando o ângulo de flexão é de 90 graus. A fórmula de cálculo para cada material é a seguinte:
De fato, simplificando a equação (7) e definindo o ângulo de flexão para 90 graus, a constante pode ser calculada e a equação pode ser transformada da seguinte forma:
BA = (1,57 * K * T) + (1,57 *R)
Portanto, comparando a fórmula de cálculo acima, o valor de K para materiais de latão macio ou cobre macio pode ser obtido como 1,57xk = 0,55, ou K = 0,35.
Usando o mesmo método, é fácil calcular os valores do fator K para os diversos tipos de materiais listados acima.
Conforme discutido anteriormente, há várias fontes das quais o valor do fator K pode ser obtido, como fornecedores de materiais, dados de testes, experiência e manuais.
Para estabelecer um modelo preciso de chapa metálica usando o método do fator K, é fundamental encontrar a fonte apropriada de fator K que atenda aos seus requisitos de engenharia. Isso garantirá que os resultados da peça física sejam tão precisos quanto desejado.
Em algumas situações, pode não ser possível obter resultados precisos usando apenas um único valor de fator K, especialmente quando é necessário acomodar uma ampla gama de cenários de flexão.
Nesses casos, é aconselhável usar o valor da tolerância à flexão (BA) diretamente para uma única flexão de toda a peça ou usar uma tabela de flexão para descrever os diferentes valores de BA, dedução de flexão (BD) ou fator K correspondentes a diferentes valores de A, R e T em toda a faixa.
Além disso, as equações podem ser usadas para gerar dados como a tabela de curvatura de amostra fornecida pelo SolidWorks. Se necessário, as células da tabela de dobras também podem ser modificadas com base em dados experimentais ou empíricos.
O diretório de instalação do SolidWorks inclui tabelas de tolerância de dobra, tabelas de dedução de dobra e tabelas de fator K, que podem ser editadas e personalizadas conforme necessário.
Esta publicação fornece uma visão geral abrangente dos métodos de cálculo comuns e seus princípios subjacentes usados no projeto e na fabricação de peças de chapa metálica.
Ele abrange o cálculo de tolerâncias de flexão, deduções de flexão e fatores K, e explica as diferenças entre esses métodos e suas inter-relações.
Ele serve como uma referência útil para engenheiros e profissionais técnicos do setor.
Observação:
Como fundador do MachineMFG, dediquei mais de uma década de minha carreira ao setor de metalurgia. Minha vasta experiência permitiu que eu me tornasse um especialista nas áreas de fabricação de chapas metálicas, usinagem, engenharia mecânica e máquinas-ferramentas para metais. Estou sempre pensando, lendo e escrevendo sobre esses assuntos, esforçando-me constantemente para permanecer na vanguarda do meu campo. Permita que meu conhecimento e experiência sejam um trunfo para sua empresa.
PT_BR 
EN 
AR 
DE 
ES 
FR 
IT 
JA 
NL 
PT 
RU 
KO