Frequência natural vs. frequência ressonante: Explicação da diferença

Na análise diária, muitas vezes confundimos a frequência natural com a frequência de ressonância e achamos que são a mesma coisa.

De fato, isso não é rigoroso.

A frequência natural é o desempenho das características naturais da estrutura, enquanto a frequência de ressonância é o desempenho da resposta estrutural sob forças externas.

Vibração livre de um sistema de molas com um único grau de liberdade

Um sistema com um único grau de liberdade é um sistema em que a posição pode ser totalmente determinada por apenas uma coordenada generalizada em um determinado momento. Em termos mais simples, a força que atua em um corpo está em apenas uma direção. O movimento da boneca na figura abaixo pode ser representado como um sistema massa-mola.

Um modelo simplificado do sistema de massa da mola pode ser mostrado na figura a seguir.

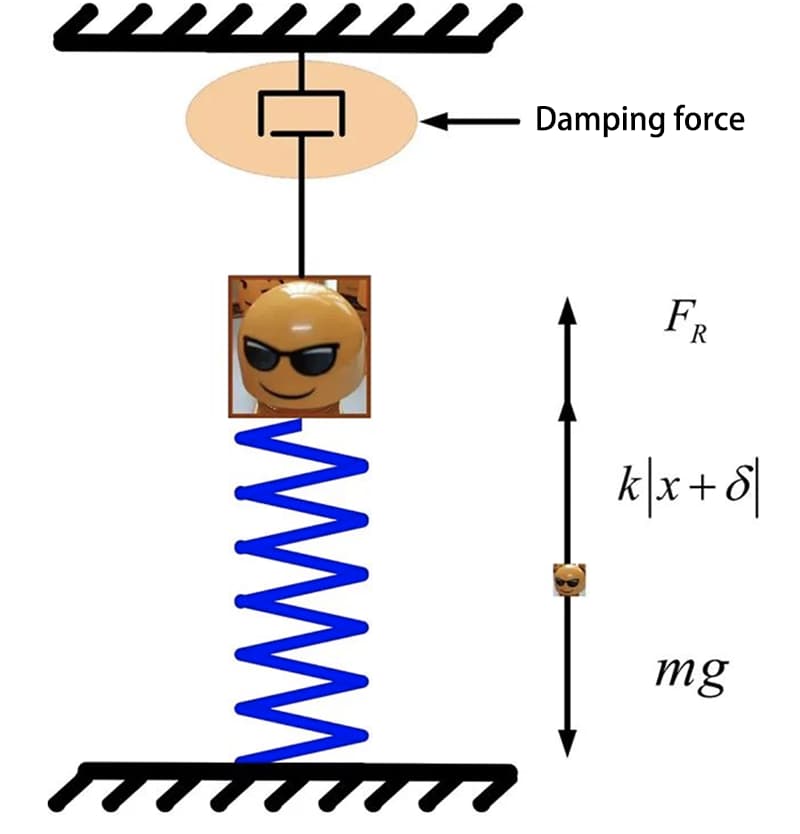
A posição de equilíbrio estático do bloco de captação é considerada a origem da coordenada e é considerada positiva quando se move verticalmente para baixo ao longo da direção da deformação da mola. A distância entre o bloco e a posição de equilíbrio pode ser representada como x, e a equação diferencial de movimento do bloco pode ser expressa como:

Onde m é a massa do bloco, k é a rigidez da mola, c é o coeficiente de viscosidade, 2n=c/m é o coeficiente de atenuação de amortecimento e, quando o coeficiente de amortecimento é zero, corresponde ao sistema de vibração sem amortecimento.

Frequência natural Pn:

A frequência natural depende apenas da massa e da rigidez e não é afetada por fatores como o amortecimento. Conexões estruturais de contorno, propriedades do materialO formato, a forma e outros fatores podem afetar a frequência natural, mas essas influências são refletidas na rigidez e na massa e não são os fatores determinantes finais.

Vibração forçada do sistema de molas sob excitação harmônica

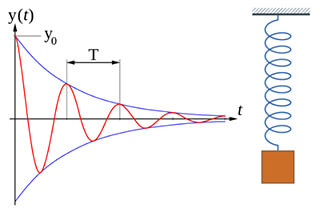
A vibração livre é a vibração do sistema sem excitação externa, e o rastro do movimento está relacionado ao estado inicial e às características naturais.

A vibração forçada refere-se à vibração gerada pelo sistema sob excitação externa.

A excitação externa é geralmente uma função periódica ou aperiódica do tempo, entre as quais a excitação harmônica simples é a mais simples.

Seja a força de excitação harmônica simples:

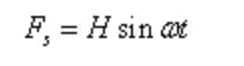
Onde, H é a amplitude da força de excitação, ω é a frequência angular da força de excitação.

Quando o bloco se desvia da posição de equilíbrio em uma distância x, a equação diferencial de movimento do bloco é

Onde, h=H/m, a equação acima é a equação diferencial da vibração forçada de grau único de liberdade com amortecimento viscoso, que é uma equação diferencial ordinária não homogênea linear de coeficiente constante de segunda ordem.

A equação acima é totalmente consistente com a expressão de resposta de tensão de carga capacitiva que aprendemos na teoria de circuitos, que é uma equação diferencial ordinária não homogênea linear de coeficiente constante de segunda ordem.

O amortecimento no circuito depende da resistência, porque a resistência apenas consome e não armazena energia.

Sob excitação harmônica simples, a solução total da equação diferencial de movimento de um sistema amortecido é definida como:

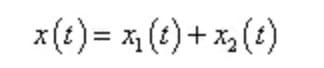
Onde x1 (t) é uma solução homogênea, que é uma vibração livre atenuada;

Devido à existência de amortecimento, a parte da vibração amortecida desaparecerá após um determinado período de tempo.

Sua solução é a mesma que a da vibração livre, portanto, não será repetida aqui.

Aqui estamos preocupados com a solução especial x₂ (t) gerado por vibração forçada, que pode ser expresso como:

Entre eles,

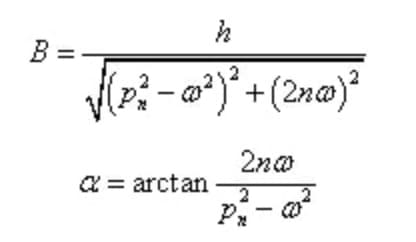
A amplitude e a defasagem de fase da vibração forçada em estado estável são independentes das condições iniciais, mas dependem apenas das características do sistema e da excitação.

Defina a taxa de frequência, a taxa de amortecimento e o coeficiente de amplificação de amplitude como:

A fórmula acima pode ser reescrita como:

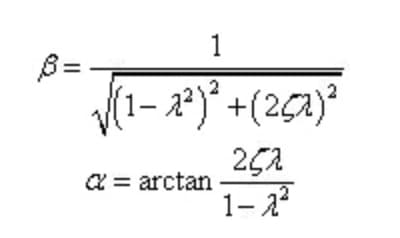
Com base nisso, podemos conhecer a resposta do sistema sob a vibração forçada.

Para melhor compreensão, a relação entre diferentes índices de amortecimento, índices de frequência e coeficientes de amplificação de amplitude pode ser ilustrada. A frequência é separada em três regiões: baixa frequência, média frequência e alta frequência. Como visto na figura, nas áreas de baixa e alta frequência, o amortecimento tem um impacto mínimo sobre o coeficiente de amplificação de amplitude. Assim, o sistema com amortecimento pode ser simplificado como um sistema sem amortecimento para facilitar o cálculo.

Frequência natural e frequência ressonante

A frequência natural é uma característica inerente das propriedades estruturais de um sistema, determinada exclusivamente por sua massa e rigidez, independentemente de fatores externos, como o amortecimento. Em um sistema com n graus de liberdade, existem n frequências naturais distintas, enquanto os sistemas contínuos possuem um número infinito de frequências naturais.

A ressonância ocorre quando uma frequência de excitação externa se aproxima ou coincide com a frequência natural de um sistema, fazendo com que a estrutura vibre com uma amplitude significativamente maior. Esse fenômeno é representado pelo círculo azul na figura ao lado. A frequência ressonante, embora muitas vezes se aproxime da frequência natural em sistemas levemente amortecidos, pode se desviar dela em estruturas altamente amortecidas, sendo normalmente menor que a frequência natural.

No projeto do sistema, é fundamental evitar não apenas a frequência de pico ressonante específica, mas também a banda ressonante circundante, correspondente à região de frequência intermediária na figura. Essa precaução é necessária porque a resposta do sistema permanece consideravelmente amplificada dentro dessa banda. Os engenheiros devem garantir que nem a operação normal do sistema nem as excitações externas de equipamentos próximos estejam dentro dessa faixa crítica.

A ressonância pode ter implicações profundas, tanto benéficas quanto prejudiciais. Os efeitos negativos podem incluir o colapso de vigas de elevação, ressonância do solo em helicópteros, danos ao maquinário e falhas estruturais induzidas por infrassom. Por outro lado, a ressonância é utilizada deliberadamente em instrumentos musicais para produzir tons e harmônicos desejados.

Para atenuar os riscos associados à ressonância, os projetistas empregam várias estratégias:

1. Ajuste de frequência: Ajuste da frequência natural do sistema para evitar faixas de frequência operacional.
2. Aumento do amortecimento: Incorporação de materiais ou mecanismos para dissipar a energia vibracional.
3. Reforço estrutural: Aumento da rigidez para alterar as frequências naturais e reduzir as amplitudes.
4. Isolamento de vibração: Implementação de sistemas para minimizar a transmissão de excitações externas.
5. Controle ativo: Utilização de sensores e atuadores para neutralizar vibrações ressonantes em tempo real.

Compreender e gerenciar a ressonância é essencial em campos que vão desde a engenharia civil e aeroespacial até a fabricação de precisão e o design de instrumentos musicais. Ferramentas analíticas avançadas, como a análise de elementos finitos e a análise modal experimental, desempenham papéis fundamentais na previsão e na caracterização do comportamento ressonante em sistemas complexos.