Você já se perguntou por que alguns materiais se dobram facilmente enquanto outros permanecem rígidos? Este blog mergulha no fascinante mundo do módulo de elasticidade e da rigidez, desvendando suas funções cruciais na engenharia. Ao final, você entenderá como essas propriedades influenciam a resistência e a flexibilidade dos materiais do cotidiano.
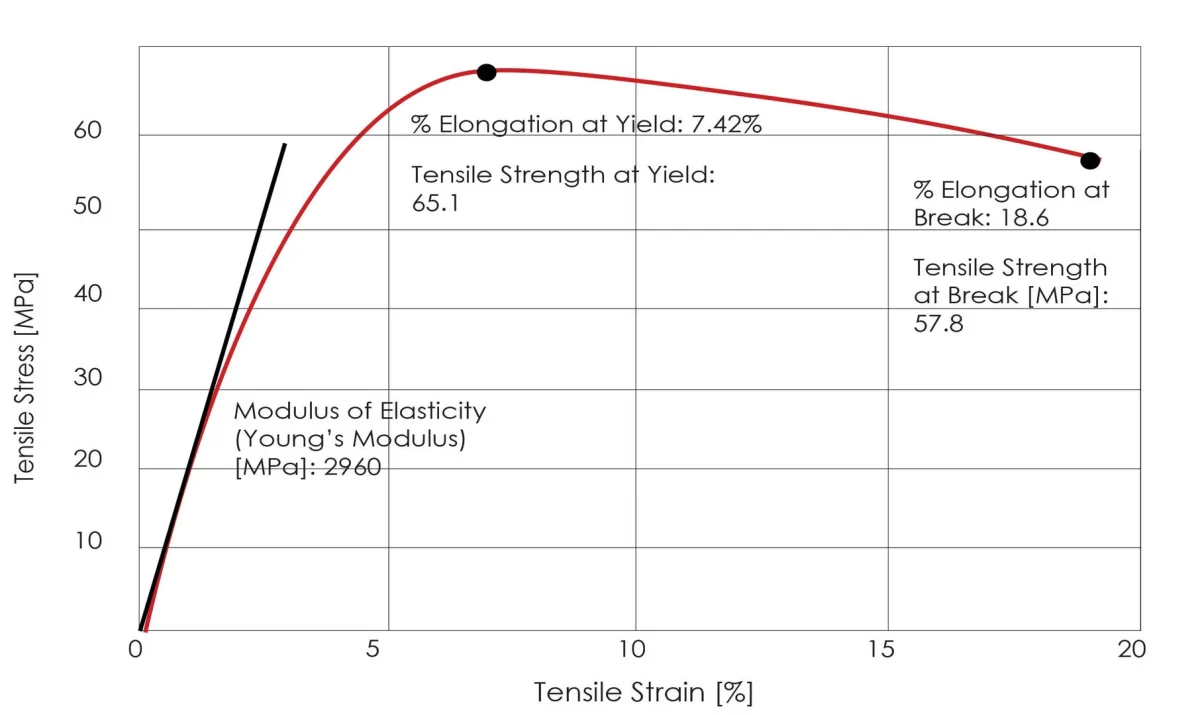
Módulo de elasticidade: A razão entre a tensão normal e a deformação normal correspondente no estágio de deformação elástica de um material.
No estágio de deformação elástica, a tensão e a deformação de um material são proporcionais, de acordo com a Lei de Hooke, e o coeficiente de proporcionalidade é chamado de módulo de elasticidade.
O termo "módulo de elasticidade" é uma descrição geral da elasticidade de um material. Ele engloba vários módulos específicos, incluindo o módulo de Young, o módulo de cisalhamento e o módulo de massa, entre outros.
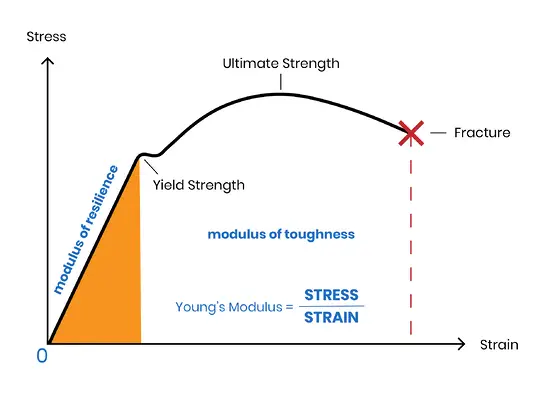
Portanto, "módulo de elasticidade" e "módulo de massa" são termos inclusivos.
Quando uma força externa (conhecida como "tensão") é aplicada a um elastômero, ele muda sua forma (conhecida como "deformação"). O módulo de elasticidade é definido como a razão entre a tensão e a deformação.
Por exemplo:
Deformação linear:
Quando uma força de tração F é aplicada a uma haste fina, a tensão linear é calculada como a força de tração dividida pela área da seção transversal S da haste.
A deformação linear é calculada como o alongamento da haste (dL) dividido por seu comprimento original (L).
A tensão linear dividida pela deformação linear é igual ao módulo de Young, E = (F / S) / (dL / L).
Deformação por cisalhamento:
Quando uma força lateral (geralmente uma força de atrito) f é aplicada a um elastômero, ele muda de um formato quadrado para um formato de diamante.
Esse ângulo de deformação é conhecido como "tensão de cisalhamento", e a força correspondente dividida pela área de tensão é chamada de "tensão de cisalhamento".
A tensão de cisalhamento dividida pela deformação de cisalhamento é igual ao módulo de cisalhamento, G = (f / S) / a.
Volume Strain:
Quando uma pressão geral P é aplicada ao elastômero, ela é conhecida como "tensão de volume".
A redução no volume do elastômero (-dV) dividida pelo seu volume original (V) é chamada de "tensão de volume".
A tensão de volume dividida pela deformação de volume é igual ao módulo de volume, K = P / (-dV / V).
Em geral, quando não há confusão, o módulo de elasticidade dos materiais metálicos se refere ao módulo de Young, também conhecido como módulo de elasticidade positivo.
Unidade: E (módulo de elasticidade) é medido em GPa.
O módulo elástico é um parâmetro de desempenho fundamental dos materiais de engenharia.
De uma perspectiva macro, ele mede a capacidade de um objeto de resistir à deformação elástica, enquanto de um ponto de vista micro, ele reflete a força de ligação entre átomos, íons ou moléculas.
Os fatores que afetam a força de ligação também podem afetar o módulo de elasticidade de um material, como o modo de ligação, a estrutura cristalina, a composição química, a microestrutura, a temperatura e outros.
O módulo de Young de materiais metálicos pode variar em mais de 5% devido a diferentes composições de liga, estados de tratamento térmico e deformações plásticas a frio.
Entretanto, de modo geral, o módulo de elasticidade de materiais metálicos é um índice de propriedade mecânica que não é sensível à estrutura.
A liga, o tratamento térmico (estrutura da fibra) e a deformação plástica a frio têm efeito limitado sobre o módulo de elasticidade, e fatores externos, como temperatura e taxa de carga, têm um impacto insignificante sobre ele.
Portanto, em aplicações gerais de engenharia, o módulo de elasticidade é considerado uma constante.
Unidade: GPa (gigapascal) para módulo de elasticidade.
O módulo elástico é uma medida da resistência de um material à deformação elástica.
Quanto mais alto for seu valor, maior será a tensão necessária para produzir uma certa quantidade de deformação elástica, o que significa que o material é mais rígido e sofre menos deformação elástica sob uma determinada tensão.
O módulo elástico, representado por E, é uma medida da quantidade de tensão necessária para que um material sofra uma deformação elástica unitária sob uma força externa.
Ela representa a capacidade do material de resistir à deformação elástica e pode ser comparada à rigidez de uma mola.
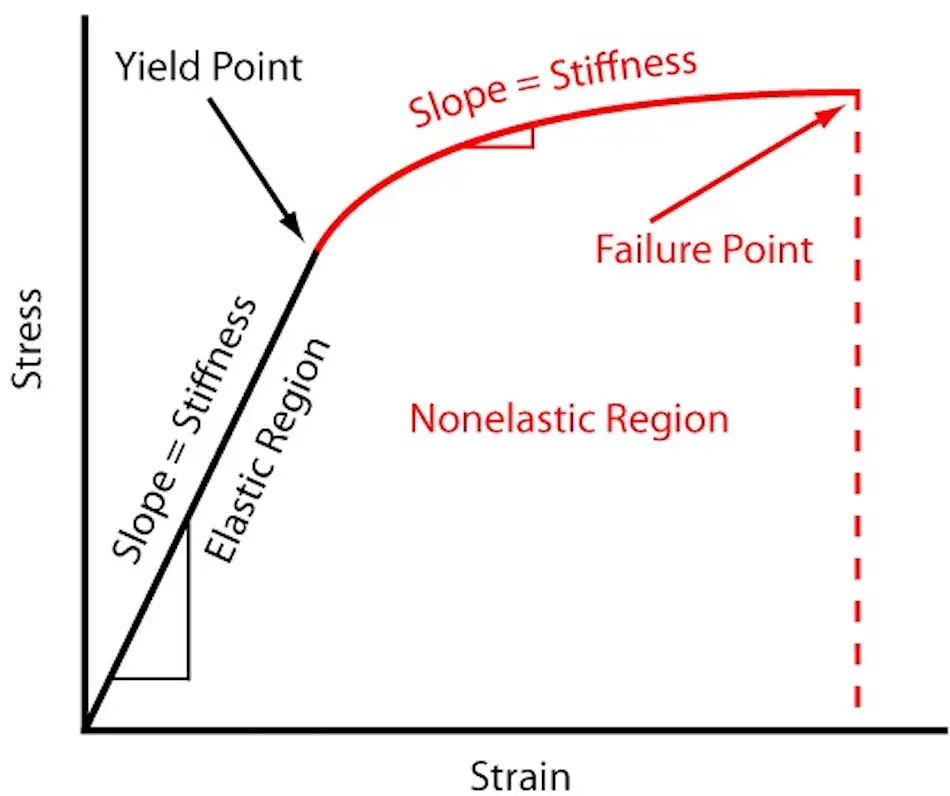
A "rigidez" refere-se à capacidade de uma estrutura ou componente de resistir à deformação elástica. Ela é determinada pela força ou momento necessário para produzir uma unidade de deformação.
Em termos de rigidez rotacional, ela é representada por "k" e pode ser calculada como "k = M / θ", em que "M" é o torque aplicado e "θ" é o ângulo de rotação.
Outras rigidezes incluem:
O método de cálculo da rigidez pode ser dividido em duas abordagens: a teoria do pequeno deslocamento e a teoria do grande deslocamento.
A teoria de grandes deslocamentos leva em conta a deformação da estrutura após o estresse e forma a equação de equilíbrio de acordo, fornecendo resultados precisos, mas com um processo de cálculo mais complexo.
Por outro lado, a teoria do pequeno deslocamento pressupõe que a estrutura não está significativamente deformada, de modo que a força interna pode ser obtida a partir da carga externa e, em seguida, usada para calcular a deformação.
Essa abordagem é amplamente usada na maioria dos aplicativos de projeto mecânico, pois é muito mais simples de resolver.
Por exemplo, no cálculo da deformação de flexão da viga, a teoria do pequeno deslocamento é frequentemente empregada porque a deformação real é muito pequena.
Essa teoria envolve ignorar a primeira derivada da deflexão na fórmula da curvatura e usar a segunda derivada da deflexão para aproximar a curvatura do eixo da viga, o que ajuda a simplificar o processo de solução ao linearizar a equação diferencial.
Quando várias cargas estão atuando simultaneamente, a deformação de flexão causada por cada carga pode ser calculada separadamente e depois combinada.
A resistência à deformação sob uma carga estática é conhecida como rigidez estática, enquanto a resistência à deformação sob uma carga dinâmica é conhecida como rigidez dinâmica, ou seja, a quantidade de força dinâmica necessária para a amplitude da unidade.
Quando a força de interferência muda lentamente (ou seja, a frequência da força de interferência é muito menor do que a frequência natural da estrutura), a rigidez dinâmica é essencialmente igual à rigidez estática.
Entretanto, se a força interferente mudar rapidamente (ou seja, a frequência da força interferente for muito maior do que a frequência natural da estrutura), a deformação estrutural será relativamente pequena e, portanto, a rigidez dinâmica será relativamente grande.
Se a frequência da força interferente estiver próxima da frequência natural da estrutura, ocorrerá a ressonância, e a rigidez dinâmica estará em seu mínimo, tornando a estrutura mais fácil de se deformar, com sua deformação dinâmica capaz de atingir várias vezes ou até mais de dez vezes a deformação da carga estática.
A deformação excessiva dos componentes pode afetar sua operação.
Por exemplo, a deformação excessiva de um eixo de engrenagem pode afetar a engrenagem, e a deformação excessiva de uma máquina-ferramenta pode reduzir a precisão da usinagem.
Os fatores que afetam a rigidez incluem o módulo de elasticidade dos materiais e a forma estrutural. A alteração da forma estrutural pode ter um impacto significativo na rigidez.
O cálculo da rigidez é a base da teoria de vibração e da análise de estabilidade estrutural. Quando a massa permanece constante, a alta rigidez resulta em uma alta frequência natural.
A distribuição de tensão em uma estrutura estaticamente indeterminada está relacionada à taxa de rigidez de cada peça.
Em mecânica da fratura o fator de intensidade de tensão de um membro rachado pode ser determinado com base em sua flexibilidade.
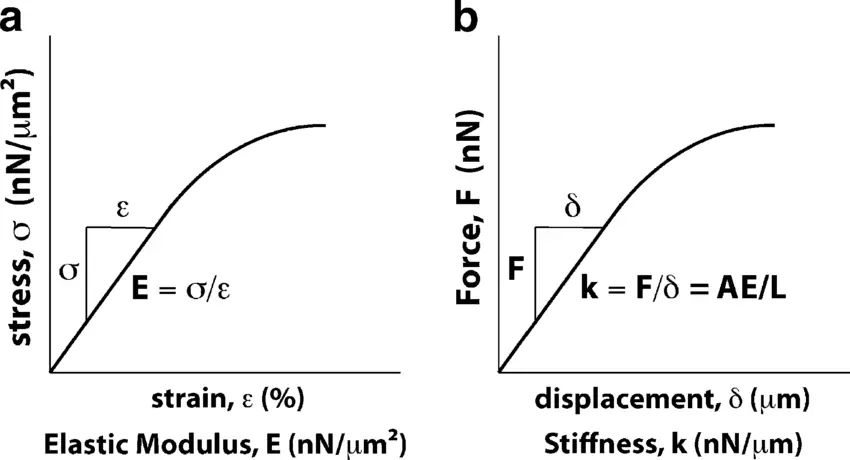
A rigidez e o módulo de elasticidade são conceitos fundamentais na ciência dos materiais, cada um descrevendo diferentes aspectos da resistência de um material à deformação. Embora estejam relacionados, eles desempenham funções distintas na análise e aplicação de materiais.
O módulo elástico, também conhecido como módulo de Young, é uma medida específica da capacidade inerente de um material de resistir à deformação sob tensão. Ele quantifica a relação entre a tensão (força por unidade de área) e a deformação (deformação proporcional) na região elástica linear da curva de tensão-deformação do material. O módulo de elasticidade é uma propriedade do material e independe da forma ou do tamanho do material. Ele é expresso em unidades de pressão, como Pascal (Pa).
A rigidez, por outro lado, é um termo mais amplo que se refere à resistência de uma estrutura à deformação elástica sob uma carga aplicada. Não se trata apenas de uma propriedade do material, mas também depende da geometria e das condições de contorno da estrutura. Em geral, a rigidez é expressa como a força necessária para atingir um deslocamento unitário (por exemplo, Newtons por metro, N/m).
A rigidez de um elemento estrutural pode ser derivada do módulo de elasticidade do material e da geometria do elemento. Por exemplo, a rigidez de flexão (EI) de uma viga é o produto do módulo de elasticidade (E) e o momento de inércia (I) da seção transversal da viga. Da mesma forma, a rigidez torcional (GI) é o produto do módulo de cisalhamento (G) e do momento polar de inércia (I).
A rigidez é fundamental no projeto de engenharia, principalmente para componentes que precisam manter sua forma sob carga, como fusos, trilhos-guia e parafusos de avanço. Ela também é essencial para estruturas que exigem controle rigoroso de deformação, como asas de aeronaves e montagens de alta precisão.
Resistência é a capacidade de um material de resistir à deformação permanente e à fratura sob forças externas. Ela abrange vários tipos de resistência, incluindo resistência ao escoamento, resistência à tração, resistência à compressão e resistência à flexão. Essas propriedades são essenciais para determinar a capacidade de suporte de carga e a durabilidade das peças mecânicas.
Compreender a distinção entre rigidez e módulo de elasticidade é essencial para projetar e analisar componentes e estruturas mecânicas. Enquanto o módulo de elasticidade fornece uma medida da resistência intrínseca de um material à deformação, a rigidez considera as propriedades do material e os fatores geométricos para descrever a resistência geral de uma estrutura à deformação. Ambos os conceitos são essenciais para garantir o desempenho e a confiabilidade dos projetos de engenharia.
Como fundador do MachineMFG, dediquei mais de uma década de minha carreira ao setor de metalurgia. Minha vasta experiência permitiu que eu me tornasse um especialista nas áreas de fabricação de chapas metálicas, usinagem, engenharia mecânica e máquinas-ferramentas para metais. Estou sempre pensando, lendo e escrevendo sobre esses assuntos, esforçando-me constantemente para permanecer na vanguarda do meu campo. Permita que meu conhecimento e experiência sejam um trunfo para sua empresa.
PT_BR 
EN 
AR 
DE 
ES 
FR 
IT 
JA 
NL 
PT 
RU 
KO