Você já se perguntou por que os eixos de transmissão são geralmente circulares? Este artigo analisa as razões mecânicas por trás desse formato, explicando como uma seção transversal circular otimiza o desempenho de torção e minimiza o estresse. Você conhecerá as vantagens desse design na resistência à deformação e na garantia de uma transmissão de potência eficiente. No final, você entenderá por que o design circular é fundamental para manter a integridade mecânica sob cargas variáveis. Continue lendo para descobrir os princípios de engenharia que tornam o eixo de transmissão circular a escolha preferida em sistemas mecânicos.
(1) Convenção sobre símbolos de torque
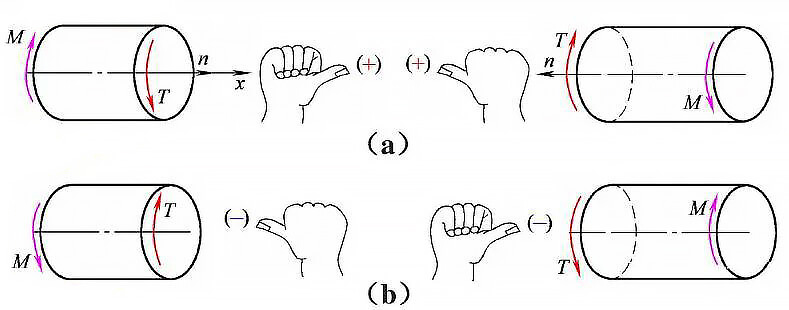
Fig. 1 Direção e símbolo do torque
(2) Deformação por torção da barra de seção circular
Após torcer um eixo com seção transversal circular, a forma e o tamanho da seção permanecem os mesmos e ela permanece plana. O raio da seção permanece como o eixo em torno do qual a seção é torcida, e cada seção gira apenas um pequeno ângulo γ em relação à outra.
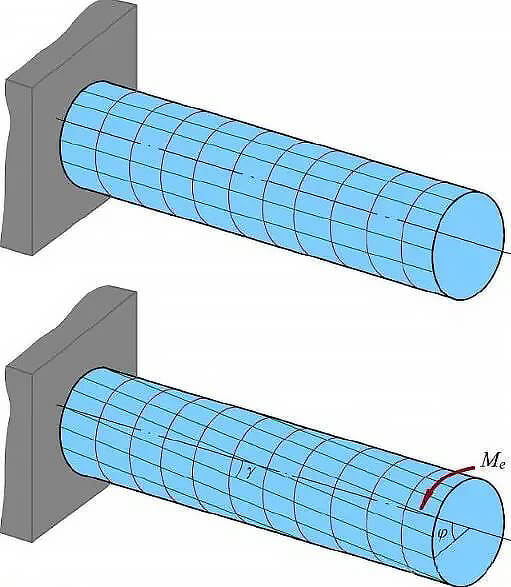
Fig. 2 Deformação por torção da barra de seção circular
(3) Torção de barra de seção não circular
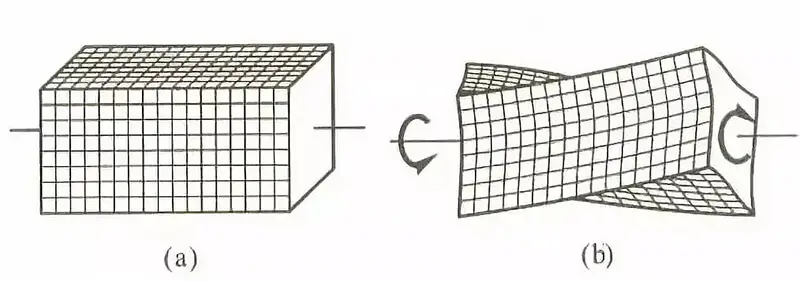
Fig. 3 Deformação por torção da barra quadrada
Torção livre:
Quando uma barra tiver uma seção transversal não circular, ela se deformará durante a deformação por torção. O grau de empenamento das seções transversais adjacentes será o mesmo, o que significa que o comprimento de todas as fibras longitudinais da barra não será alterado. Nesse cenário, não haverá tensão normal na seção transversal, apenas tensão de cisalhamento.
Para obter torção livre, as duas extremidades da barra reta devem ser submetidas a um torque externo, e o empenamento das seções adjacentes não deve ser restringido externamente.
Torção restrita:
Quando uma barra reta não uniforme é torcida, a quantidade de torque aplicada muda ao longo do comprimento da barra. Se uma extremidade da barra for fixa e não puder se mover, o grau de deformação das seções adjacentes da barra será diferente. Além da tensão de cisalhamento, também haverá tensão normal na seção transversal da barra.
Normalmente, a tensão normal causada pela torção restrita em uma barra sólida é pequena e pode ser desprezada. No entanto, em barras de paredes finas, essa tensão normal costuma ser muito grande para ser ignorada.
(1) Hipótese do plano
Após a torção, a seção circular permanece plana, e sua forma, tamanho e raio permanecem inalterados. As seções giram em relação umas às outras apenas por um pequeno ângulo γ. No entanto, essa suposição se aplica apenas ao eixo da seção circular e não ao eixo das seções não circulares.
O espaçamento entre as seções adjacentes permanece o mesmo, exceto quando τzx = τzy, o que indica que não há tensão normal.
σ x= σ y= σ z= τ xy=0.
O modelo de elasticidade é mostrado na Fig. 4.

Fig. 4 Modelo mecânico elástico de torção de uma barra reta
(2) Manalogia da embraiagem
Prandtl apontou que a curvatura de um filme líquido fino, também conhecido como membrana, sob pressão uniforme é matematicamente semelhante à função de tensão no problema de torção de uma barra reta com seção transversal igual.
A comparação da barra de torção com a membrana pode ser útil para resolver o problema de torção.
Na Figura 5, há um filme uniforme esticado em um limite horizontal, que tem a mesma forma e tamanho que o limite da seção transversal de uma barra de torção.
Quando uma pequena pressão uniforme é aplicada ao filme, cada ponto do filme sofrerá uma pequena queda.
Se o plano em que o limite está localizado for o plano xy, a inclinação pode ser representada por z.
Devido à natureza flexível do filme, supõe-se que ele não possa suportar momento de flexão, torque, força de cisalhamento ou pressão. Ele suporta apenas uma força de tração uniforme FT, que é semelhante à tensão superficial do filme líquido.
De acordo com essa análise, a tensão de cisalhamento em qualquer ponto da seção transversal da barra de torção, em qualquer direção, é igual à inclinação do filme na direção vertical naquele ponto.
Pode-se observar que a tensão de cisalhamento máxima na seção transversal da barra de torção é igual à inclinação máxima da membrana. No entanto, deve-se observar que a direção da tensão máxima de cisalhamento é perpendicular à direção da inclinação máxima.
Com essa suposição, é possível determinar a tensão máxima de cisalhamento e o ângulo de torção relativo da barra reta de seção não circular listada na Tabela 1 abaixo.

Fig. 5 Modelo de analogia de membrana
(1) Eixo circular sólido
De acordo com as premissas 1 e 2, as propriedades mecânicas dos materiais plásticos em cisalhamento puro quando os materiais componentes estão dentro da faixa elástica:
τ= G γ,γ É a deformação de cisalhamento;
γ=φ R/L( γ é o ângulo de torção relativo de duas seções a uma distância L;
φ é o canto da face da extremidade de torção, R é o raio externo do círculo e L é o espaçamento entre duas seções).

Fig. 6 Diagrama esquemático da torção da barra com seção circular sólida
A tensão de cisalhamento em ρ na seção circular é:

Sob a mesma condição de torque, a tensão de cisalhamento (τ) em uma barra de seção transversal circular é proporcional à distância do centro da seção (ρ). Isso significa que quanto maior for a distância do centro, maior será a tensão de cisalhamento.
Quando a distância do centro é igual ao raio (R) da seção circular, a tensão de cisalhamento máxima é obtida na borda.
O módulo de seção de torção (Wp) de um eixo circular pode ser expresso como IP/R, em que IP é o momento polar de inércia. Esse valor está relacionado apenas às dimensões geométricas da seção e não à área da seção transversal.
A tensão de cisalhamento máxima (τ max) pode ser calculada como T/WP, em que T é o torque aplicado.
Para um eixo sólido com uma seção circular, o módulo de seção de torção (WP) é aproximadamente igual a 0,2 vezes o cubo do diâmetro (D).
O ângulo de torção (φ) de uma barra redonda sob torção está relacionado à rigidez de torção (GIP) da seção circular, que reflete a capacidade do eixo de resistir à deformação.
Os ângulos de torção relativos de duas seções a uma distância de L podem ser calculados usando uma fórmula de torção.
Ângulo relativo de torção:
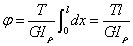
Condição de rigidez do eixo circular:

(2) Eixo circular oco
O coeficiente de torção da seção do eixo circular oco é aproximadamente: WP ≈ 0,2D3 (1- α 4),0< α= d/D<1.
Quando α= 0,8, o WP é 60% da seção circular sólida, ou seja, sob o mesmo torque, a resistência diminui em 40%, mas sob o mesmo material e comprimento, a diferença de peso é 2,8 vezes.
(3) Tubo fechado de parede fina
Um tubo redondo com uma espessura de parede (a) muito menor do que seu raio (R0) - normalmente considerado ≤ R0/10 - é conhecido como um tubo redondo de parede fina. Esse tipo de tubo pode ter qualquer formato e seção igual.
Como se trata de um tubo de parede fina, supõe-se que a tensão de cisalhamento seja uniformemente distribuída por toda a espessura da parede (t) para obter uma solução aproximada.
Aplicando a regra da tensão de cisalhamento recíproca, pode-se concluir que o produto da tensão de cisalhamento axial média de todos os pontos na seção do tubo e na parede do tubo é igual, ou seja, o fluxo de cisalhamento (q) é constante.
Como o valor de q é consistente em toda a seção, a tensão de cisalhamento máxima está na espessura mínima da parede.
Quando a seção do tubo é circular, sua área (Am) é igual a πR0². O aumento do diâmetro do cilindro pode reduzir significativamente a tensão de cisalhamento.

Fig. 6 Distribuição da tensão de cisalhamento de várias seções comuns
Durante o teste de torção, a distribuição de tensão na seção transversal do corpo de prova é desigual. A superfície sofre a maior quantidade de tensão e, à medida que nos movemos em direção ao centro, a tensão diminui.
Como resultado, quando o material é torcido, o dano começa na camada mais externa da haste redonda e progride em direção ao interior. A rachadura se inicia na camada superficial e se propaga para dentro.
Na engenharia, o teste de torção é comumente utilizado para examinar os defeitos de superfície e o desempenho de endurecimento de superfícies camadas em materiais.
Conforme mostrado na Fig. 7.

Fig. 7 Teste de torção da amostra de barra redonda
No processo de torção de um eixo circular feito de materiais plásticos, como o aço de baixo carbono, a superfície do eixo cederá primeiro e, em seguida, a circunferência será cortada ao longo da seção à medida que a deformação por torção aumentar.
Isso se deve ao fato de que a capacidade de cisalhamento do material é menor do que sua capacidade de tração, e a tensão máxima de cisalhamento ocorre na seção transversal, resultando em falha de cisalhamento.
Na engenharia, a tensão máxima de cisalhamento na borda externa da seção transversal geralmente é definida como o limite de escoamento de cisalhamento do material (τs) como o estado perigoso, e a condição de resistência é estabelecida com base nisso.
No entanto, mesmo quando a tensão de cisalhamento na borda atinge o limite de rendimento, as outras peças ainda estão no estado de trabalho elástico linear, e a haste redonda não sofrerá deformação plástica óbvia, permitindo que o torque continue a aumentar.
Levando em consideração a plasticidade do material, o torque final (torque plástico) de uma haste redonda sólida é 1/3 maior do que o torque de rendimento (que é o resultado de um cálculo de engenharia simplificado).
Quando a tensão de cisalhamento na borda da seção transversal do material atinge o limite de escoamento de cisalhamento do material τs, a região plástica se expande gradualmente para dentro com o aumento do momento de torção, e o material na borda da seção transversal começa a se fortalecer.
Se o momento de torção continuar a aumentar, a rachadura começará na camada mais externa da haste redonda e, por fim, será cortada ao longo da seção transversal.
Conforme mostrado na Fig. 8.

Fig. 8 Teste de torção de amostra de barra redonda de material plástico
No caso de um eixo redondo feito de materiais frágeis, como ferro fundido, com uma capacidade de tração menor do que a capacidade de cisalhamento, a deformação durante a falha de torção é mínima. O eixo tende a quebrar na superfície helicoidal em um ângulo de aproximadamente 45° em relação ao eixo.
Isso ocorre porque o plano inclinado a 135° em relação ao eixo sofre a tensão máxima de tração. Se a tensão máxima de tração nessa seção exceder o limite de resistência à tração do material, o eixo falhará devido à tensão nessa seção.
Conforme mostrado na Fig. 9.

Fig. 9 Teste de torção de amostra de barra redonda de material frágil
O torque interno T recebido pela barra de toras não apenas gera uma distribuição linear radial de tensão de cisalhamento na seção transversal, mas também induz uma tensão de cisalhamento correspondente ao longo do plano axial, o que pode levar a rachaduras ao longo do plano axial.
Como a madeira é um material anisotrópico, a força de cisalhamento paralela às fibras ao longo da direção axial é muito menor do que a força de cisalhamento perpendicular às fibras na seção transversal, resultando no padrão de rachaduras descrito na Figura 10.

Fig. 10 Falha de torção do tronco
A figura ilustra as fórmulas de cálculo da tensão máxima e do ângulo de torção de seções quadradas, triangulares e elípticas, de acordo com a análise da teoria da elasticidade.
Em todos os casos mencionados acima, a tensão de cisalhamento máxima ocorre na linha de limite da seção mais próxima do eixo central.
Em um tubo fechado de paredes finas, a posição com a espessura de parede mais fina em relação ao eixo central sofre a maior tensão de cisalhamento.

Fig. 11 Fórmula de cálculo da tensão de cisalhamento de torção e do ângulo de torção relativo de diferentes seções
Seja S a área de um círculo, quadrado, triângulo e elipse, todos submetidos ao mesmo torque T.
O comprimento do lado de um quadrado é a = √S, enquanto o comprimento do lado de um triângulo equilátero é aproximadamente a ≈ 2,3√S.
Usando a fórmula de cálculo de tensão máxima fornecida na figura, quando submetida à mesma área de seção transversal e torque, a tensão de cisalhamento máxima na seção transversal de um triângulo equilátero é cerca de 1,8 vezes maior que a de um quadrado.
Para uma elipse com a = b, o que a torna um círculo, a = 0,56√S, e a tensão de cisalhamento máxima em um quadrado é cerca de 1,32 vezes maior que a de um círculo.
Se a elipse tiver a ≠ b, com 1 > b/a = λ > 0, então a razão entre a tensão de cisalhamento máxima na elipse e a tensão de cisalhamento máxima no círculo é λ√S-2. Assim, quanto menor for o valor de λ, maior será a tensão de cisalhamento.
Por meio da comparação acima, pode-se concluir que:
Quando um eixo tem a mesma seção e suporta o mesmo torque, a tensão de cisalhamento máxima na seção circular é a menor em comparação com uma seção não circular. Além disso, o ângulo de torção também é menor. Portanto, um eixo de transmissão circular tem uma vantagem natural no desempenho mecânico de torção.
Ampliando essas descobertas para seções transversais arbitrárias, pode-se provar que o eixo de seção transversal circular tem a maior eficiência.
Quando um eixo tem a mesma seção e suporta o mesmo torque, a tensão de cisalhamento máxima na seção circular é a menor em comparação com uma seção não circular. Além disso, o ângulo de torção também é menor. Portanto, um eixo de transmissão circular tem uma vantagem natural no desempenho mecânico de torção.
Ampliando essas descobertas para seções transversais arbitrárias, pode-se provar que o eixo de seção transversal circular tem a maior eficiência.
Tabela 1: Fórmula de verificação de torque do diâmetro do eixo
|
Tipo de eixo |
fórmula |
instrução |
|
eixo sólido |
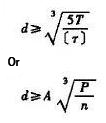 |
Onde: d - calcule o diâmetro do eixo na seção (mm) Torque de classificação T transmitido pelo eixo (N-mm) T=9550000P/n Potência nominal P transmitida pelo eixo (kW) Velocidade do eixo n (R / min) [T] - tensão de cisalhamento permitida do eixo (MPa) A - coeficiente determinado por [t], Relação V entre o diâmetro interno d0 e o diâmetro externo D do eixo circular oco |
|
eixo oco |
 |
A tensão de cisalhamento da superfície de um eixo de seção transversal circular é alta, e o centro é relativamente pequeno quando suporta carga de torção. Portanto, a remoção de parte do material que não desempenha uma função completa no centro pode reduzir efetivamente o peso do eixo e melhorar sua resistência à flexão.
No entanto, para decidir se as peças do eixo devem ou não ser ocas, é necessário considerar não apenas os fatores mecânicos, mas também os custos tecnológicos e de fabricação. É importante observar que a espessura da parede não deve ser muito fina, caso contrário, podem ocorrer dobras locais, levando a uma perda da capacidade de suporte.
Quando a espessura da parede (δ) do cilindro é muito menor do que o raio (R0), que geralmente é considerado ≤ R0/10, ele é chamado de cilindro de parede fina. Entretanto, se o tubo de parede fina tiver uma abertura longitudinal ao longo do eixo, sua resistência à torção diminuirá significativamente. Portanto, geralmente é adicionado um diafragma para melhorar sua resistência à torção. rigidez e resistência.
Normalmente, um eixo é composto de várias seções, e a concentração de tensão na posição de transição entre essas seções é uma causa comum de falha nas peças do eixo.
A literatura pode ser consultada para orientação sobre como selecionar e determinar o diâmetro maior de duas seções adjacentes e o filete de transição.
A mola helicoidal cilíndrica é um componente comum na engenharia mecânica, caracterizado por seu eixo em espiral e grande deformação elástica.
No projeto de uma mola Com uma mola com alta capacidade de carga, a resistência é normalmente a principal consideração. Entretanto, para uma mola com baixa capacidade de carga, a deformação é geralmente o principal fator a ser considerado.
Para molas menos críticas, a seleção pode se basear apenas nas dimensões e especificações estruturais.
Para obter informações sobre métodos de projeto e cálculo de molas, consulte a literatura pertinente, bem como as normas da série GB/T1239, GB/T2089, DIN2089 e outras normas aplicáveis.
Sob a ação da carga estática, há uma certa relação entre as propriedades mecânicas dos materiais em torção e tração, de modo que [σA tensão de cisalhamento permissível[ τ]: de materiais é usada para determinar a tensão de cisalhamento permissível[ τ]:
| Tipo de material | [σ] | [ τ] | [ τ] |
| material plástico | 1 | 0.5~0.7 [σ] | 0,55 ou 0,577 [σ] |
| Material frágil | 1 | 0.7~1.0 [σ] | 0.8~1.0 [σ] |
A tabela acima destaca que a relação entre a tensão de cisalhamento e a tensão normal fornecida na literatura é diferente.
Vários materiais plásticos mencionados na literatura mostram que a relação entre a tensão de cisalhamento e a tensão normal deve estar entre 0,5 e 0,7 [σ].
No entanto, essa relação é uma estimativa aproximada e só deve ser usada quando os dados exatos da tensão de cisalhamento não estiverem disponíveis.
Para uma verificação precisa, é necessário obter o valor específico da resistência à torção do material.