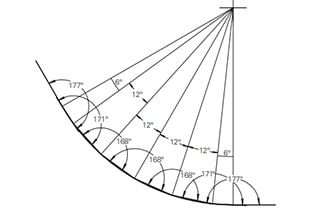
Você já teve dificuldades para desdobrar peças de chapa metálica com precisão? Este artigo explora a arte e a ciência por trás dos cálculos de desdobramento de chapas metálicas. Descubra os principais conceitos, fórmulas e técnicas usados por engenheiros experientes para desdobrar com precisão geometrias complexas. Saiba como aplicar esses princípios em seus próprios projetos e otimizar seu processo de fabricação.
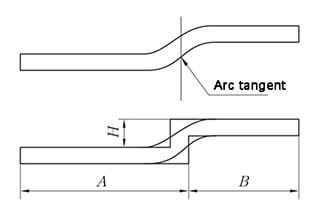
A primeira etapa do processo de fabricação de chapas metálicas é o desdobramento das geometrias e do corpo coerente. A precisão e a correção do desdobramento da amostra afetam diretamente a qualidade da peça final.
No passado, devido às limitações das ferramentas de cálculo, as pessoas usavam o método de projeção para ampliar a amostra em um plano com uma proporção de 1:1 e medir o comprimento real da linha de plano necessária.
No entanto, esse método é complicado e ineficiente, e não consegue atender às demandas atuais de produção.
Com os avanços nas ferramentas de cálculo, como as calculadoras eletrônicas e o uso generalizado de computadores, chapa metálica agora pode ser realizado usando métodos de cálculo.
Para padronizar o método de cálculo do coeficiente de desdobramento de chapas metálicas pelos técnicos, minimizar os desvios dimensionais dos produtos após a dobra e facilitar a autoinspeção pelo pessoal da oficina e a reinspeção pelos inspetores de qualidade, há um padrão e uma base unificados para o coeficiente de desdobramento.
Como resultado, o padrão de cálculo para o coeficiente de desdobramento de chapas metálicas tem se tornado cada vez mais padronizado.
Método de desdobramento de camada neutra
No processo de flexão, a camada externa sofre tensão de tração, enquanto a camada interna sofre tensão de compressão. A camada de transição entre a tensão de tração e a compressão é chamada de camada neutra. O comprimento da camada neutra durante a flexão permanece o mesmo que antes da flexão, o que a torna a referência para determinar o comprimento desdobrado da peça flexionada.
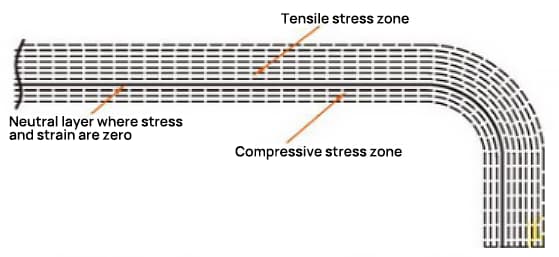
A localização da camada neutra depende do grau de deformação.
A posição da camada neutra não está relacionada apenas ao raio de curvatura, à espessura da chapa, ao coeficiente de deslocamento interno etc., mas também a fatores como o método de processamento, o formato e o tamanho da chapa metálica.
Portanto, a posição da camada neutra só pode ser determinada de forma aproximada e, em aplicações práticas, geralmente são usados valores aproximados para o cálculo.
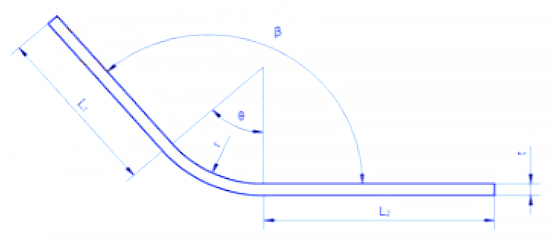
A fórmula de cálculo para a dimensão do comprimento L da camada neutra é:
Entre eles,
Usando software 3D para realizar simulações e cálculos de várias espessuras, ângulos e raios, juntamente com práticas de fabricação no local, compilamos um conjunto de valores de fator K. Consulte a Tabela 1 para obter os valores específicos.
Tabela 1: Valores K do coeficiente da camada neutra
| r/t | ≤05 | 0.6 | 0.8 | 1 | 1.2 | 1.3 | 1.5 | 2 | 2.5 | 3.0 | 4.0 | 5.0 | 6.0 | ≥8 |
| k | 026 | 0.28 | 0.30 | 0.32 | 0.33 | 0.34 | 0.36 | 0.38 | 0.39 | 0.4 | 0.42 | 0.44 | 0.46 | 0.5 |
Cálculo de desdobramento rápido para curvas de 90°
O diagrama de desdobramento para uma curva de 90° é mostrado na Figura 9. Nos últimos anos, usamos softwares 3D como CATIA e SOLIDWORKS para modelagem de chapas metálicas para calcular as dimensões de desdobramento.
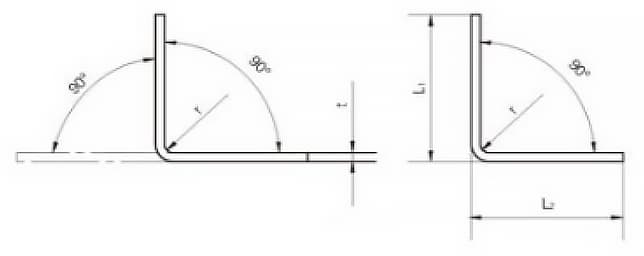
Por meio de verificações repetidas, observou-se que, quando o ângulo de flexão a frio de produtos de aço planos é de 90°, a fórmula para calcular o comprimento desdobrado L é:
L = L1 + L2 - A
Onde,
Tabela 2 Tabela de parâmetros de flexão de 90
| Espessura t/mm | Raio de assentamento r/mm | |||||||||||
| 1 | 1.2 | 16 | 2 | 25 | 3 | 4 | 5 | 6 | 8 | 10 | 12 | |
| Valor de compensação A mm | ||||||||||||
| 1 | -1.92 | -1.97 | -2.10 | -2.23 | -2.41 | -2.59 | -2.97 | -3.36 | -3.79 | -4.65 | -5.51 | -6.37 |
| 1.5 | -2.90 | -3.02 | -3.18 | -3.34 | -3.70 | -4.07 | -4.45 | -5.26 | -6.11 | -6.97 | ||
| 2 | -3.84 | -3.98 | -4.13 | -4.46 | -4.81 | -5.18 | -5.94 | -6.72 | -7.58 | |||
| 2.5 | -4.80 | -4.93 | -5.24 | -5.57 | -5.93 | -6.66 | -7.42 | -8.21 | ||||
| 3 | -5.76 | 6.04 | -6.35 | -6.69 | -7.40 | -8.14 | -8.91 | |||||
| 4 | -7.7 | -7.95 | -8.26 | -8.92 | -9.62 | -10.36 | ||||||
| 5 | -9.6 | -9.87 | -10.48 | -11.15 | -11.85 | |||||||
| 6 | -11.5 | -12.08 | -12.71 | -13.38 | ||||||||
| 8 | -15.4 | -15.9 | -16.51 | |||||||||
| 10 | -19.2 | -19.73 | ||||||||||
| 12 | 23.01 | |||||||||||
Quando o raio de curvatura é grande e o ângulo de flexão é pequeno, o grau de deformação é baixo e a camada neutra fica próxima ao centro da espessura da chapa.
No entanto, quando o raio de curvatura (R) se torna menor e o ângulo de flexão (θ) aumenta, o grau de deformação também aumenta e a camada neutra se move em direção ao lado interno do centro de flexão. A distância da camada neutra até o lado interno da folha é indicada por λ, e a espessura do material é indicada por T.
A fórmula básica para calcular o comprimento de desdobramento:
Comprimento de desdobramento = tamanho interno do material + tamanho interno do material + quantidade de compensação.
Você também pode usar a calculadora a seguir para calcular o comprimento de desdobramento da chapa metálica:

A seguir, descrevemos os algoritmos de desdobramento de vários recursos de dobra, um por um.
R = 0 mm, θ = 90° (Observação: quando R ≤ 1,0 mm, é tratado como R = 0 mm).
L = A + B + K
Na produção real, a matriz superior de dobra pode usar um ângulo R, ou pode haver um ângulo R menor do que 1 mm, ou a escolha do matriz inferiorpode ser grande, entre outros motivos, resultando em um coeficiente de flexão pequeno. Como resultado, o coeficiente de flexão de cada espessura de placa de material é apresentado na Tabela 1 com base em valores empíricos reais.
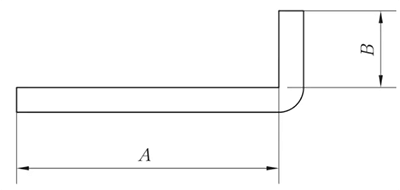
Fig. 1 Diagrama esquemático da flexão geral I
R ≠ 0mm e θ = 90°
L = A + B + K (K é o comprimento do arco da camada neutra)
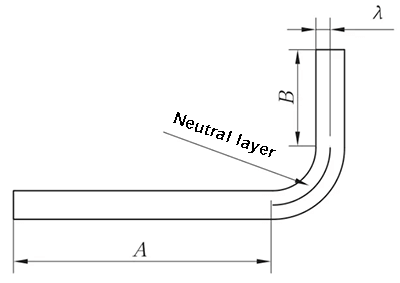
Fig. 2 Diagrama esquemático da flexão geral II
R = 0 mm, θ ≠ 90°
L = A + B + K'
Observação: K é o valor de compensação a 90°.
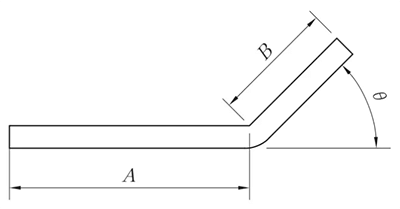
R ≠ 0mm, θ ≠ 90°
L = A + B + K
(K é o comprimento do arco da camada neutra)
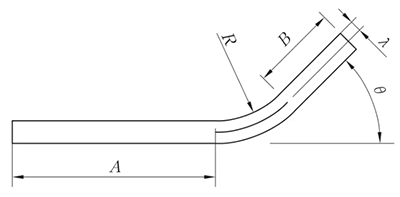
Fig. 4 Flexão geral IV diagrama de flexão
O método Unfolding é equivalente ao método Parallel Straight-Edge Z-Fold, e a medição da altura é demonstrada na Figura 6.
O ângulo θ é considerado um desdobramento de 90°.
Para 0 < T ≤ 1,6 mm, λ é igual a 0,5 T.
Quando T é maior que 1,6 mm, λ é igual a 0,4T.
Z-Fold, também conhecido como Dobra por deslocamentoA curvatura por deslocamento de borda reta e a curvatura por deslocamento de borda chanfrada são diferenciadas com base no ângulo de formação, e o método de processamento é determinado pela altura do deslocamento.
Quando a altura de deslocamento, h, é menor que 3,5 vezes a espessura do material, matrizes offset ou matrizes intercambiáveis são usadas para a formação.
Se a altura do deslocamento exceder 3,5 vezes a espessura do material, será empregada a formação positiva e negativa normal.
Quando o comprimento da borda chanfrada é inferior a 3,5 vezes a espessura do material, são usadas matrizes de deslocamento ou matrizes intercambiáveis para a formação.
Se o comprimento da borda chanfrada exceder 3,5 vezes a espessura do material, será aplicada a dobragem normal de um positivo e um negativo.
(1) Quando H < 3,5T, somente então pode ser processado por dobra de deslocamento.
L = A + B + H
(se H ≤ T, então compense 0,2 mm)
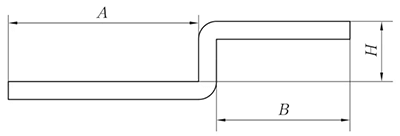
Fig. 5 Diagrama esquemático do deslocamento da borda reta
(2) Deslocamento de borda reta não paralela
O método de expansão é o mesmo que o método de dobra em Z com borda reta paralela, e o valor da altura é mostrado na Figura 6.
O ângulo θ pode ser considerado como um desdobramento de 90°.
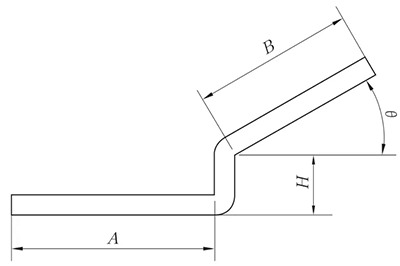
Fig. 6 Diagrama esquemático do deslocamento da borda reta não paralela
(3) Deslocamento da borda reta - o segmento de transição é tangente a dois arcos
Quando o Straight-Edge Offset é desdobrado no ponto tangente de dois arcos circulares, uma linha vertical é criada no ponto tangente dos dois arcos circulares na superfície externa do substrato. O material é então deslocado em uma espessura de material para dentro, conforme mostrado na Figura 7, para processamento e desdobramento usando o método Z-Fold 1 (Straight-Edge Offset).
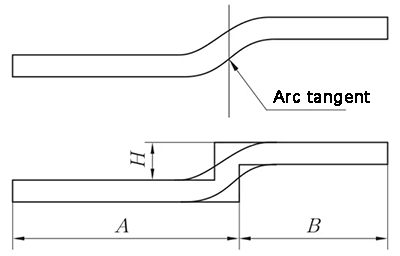
Fig. 7 Diagrama de deslocamento de borda reta - o segmento de transição é tangente a dois arcos circulares
Quando H < 2T, o algoritmo de desdobramento é o seguinte, de acordo com o processamento de deslocamento.
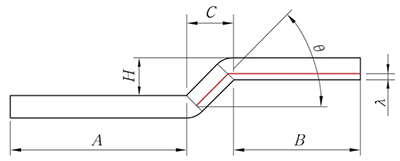
Fig. 8 Diagrama do deslocamento da borda chanfrada
L = A + B - K
(1) Ao achatar, considere pressionar a linha antes de dobrar com base nas condições reais.
O local de prensagem da linha está no centro da área de deformação por flexão.
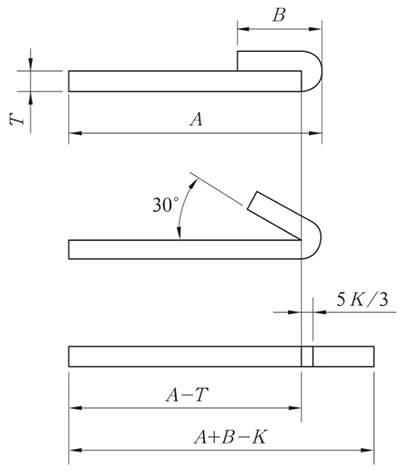
Fig. 9 Diagrama esquemático de dobragem reversa e achatamento
Os processos de dobragem reversa e achatamento geralmente são realizados em duas etapas: primeiro, o material é dobrado a 30° usando a matriz de inserção, seguido pelo achatamento.
Portanto, ao criar o linha de dobra No desenho ampliado, é essencial ilustrar a linha de dobra com base na dobra de 150°, conforme demonstrado na Figura 9.
Tabela 1: Coeficiente de flexão de placas com diferentes espessuras sob diferentes ângulos de flexão
| Ângulo | Espessura/mm | ||||
|---|---|---|---|---|---|
| 1 | 1.2 | 1.5 | 1.8 | 2.5 | |
| 45° | 5.3 | 6.3 | 7.8 | 9.5 | 13 |
| 50° | 4.5 | 5.4 | 6.8 | 8.1 | 11.25 |
| 55° | 4 | 4.7 | 5.8 | 7.05 | 9.75 |
| 60° | 3.4 | 4.1 | 5.1 | 6.15 | 8.5 |
| 65° | 3 | 3.6 | 4.5 | 5.4 | 7.5 |
| 70° | 2.65 | 3.2 | 4 | 4.75 | 6.6 |
| 75° | 2.35 | 2.8 | 3.5 | 4.25 | 5.9 |
| 80° | 2.1 | 2.5 | 3.1 | 3.75 | 5.25 |
| 85° | 1.9 | 2.25 | 2.8 | 3.35 | 4.65 |
| 90° | 1.7 | 2 | 2.5 | 3 | 4.15 |
| 95° | 1.5 | 1.8 | 2.2 | 2.7 | 3.75 |
| 100° | 1.35 | 1.6 | 2 | 2.4 | 3.35 |
| 105° | 1.2 | 1.4 | 1.75 | 2.15 | 3 |
| 110° | 1.1 | 1.3 | 1.6 | 2 | 2.65 |
| 115° | 1 | 1.25 | 1.4 | 1.7 | 2.35 |
| 120° | 0.85 | 1 | 1.25 | 1.5 | 2.1 |
| 125° | 0.75 | 0.9 | 1.1 | 1.35 | 1.85 |
| 130° | 0.65 | 0.8 | 1 | 1.18 | 1.65 |
| 135° | 0.55 | 0.7 | 0.85 | 1.05 | 1.45 |
| 140° | 0.5 | 0.6 | 0.75 | 0.9 | 1.25 |
| 145° | 0.43 | 0.5 | 0.65 | 0.77 | 1.05 |
| 150° | 0.35 | 0.43 | 0.55 | 0.65 | 0.9 |
| 155° | 0.3 | 0.35 | 0.45 | 0.53 | 0.75 |
| 160° | 0.23 | 0.27 | 0.35 | 0.4 | 0.6 |
| 165° | 0.17 | 0.2 | 0.25 | 0.3 | 0.45 |
O método de processamento N-fold envolve tanto a remodelagem quanto o achatamento, e o algoritmo para desdobramento é:
L = A + B + K
(K é o comprimento do arco da camada neutra).
λ = 0,5T
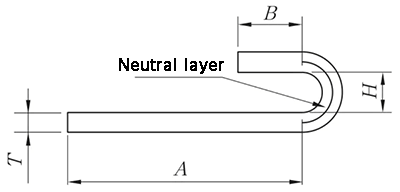
Fig.10 Diagrama N-fold
(1) A expansão do arco é diretamente K, e o comprimento do arco da camada neutra é considerado. λ= 0,5T
(2) Expansão com a borda reta em um lado.
L = A + K
(k é o comprimento do arco da camada neutra)
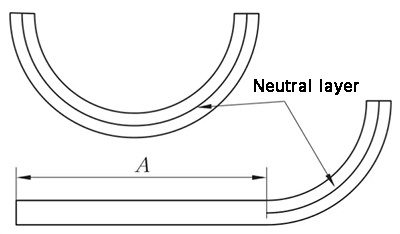
Fig. 11 Diagrama esquemático da flexão em arco
Na produção real, o controle preciso do comprimento desdobrado da chapa metálica por meio do software 3D pode ser obtido principalmente por meio das seguintes etapas e métodos:
Escolha o software de design 3D correto: Primeiro, você precisa escolher um software CAD 3D adequado para o projeto de chapas metálicas. SolidEdge, Creo, FreeCAD, UG, etc. são softwares que podem ser usados para projetos de chapas metálicas. Esses softwares oferecem módulos de chapa metálica ou funções relacionadas que podem ajudar os projetistas com o projeto e os cálculos de desdobramento de peças de chapa metálica.
Use o módulo de chapa metálica ou as ferramentas do software: A maioria dos softwares de CAD 3D oferece ferramentas e funções relacionadas ao projeto de chapas metálicas. Por exemplo, o Creo oferece uma variedade de métodos para controlar as dimensões desdobradas da chapa metálica, incluindo os métodos de modelagem e desdobramento de peças de chapa metálica de arco grande, método de dedução de dobra, etc. O FreeCAD, como um software de modelagem 3D de código aberto, também oferece um módulo de chapa metálica.
Aplicativométodos de cálculo de desdobramento de letras: Para garantir a precisão do comprimento depois que a chapa metálica é desdobrada, podem ser usados diferentes métodos de cálculo de desdobramento. Os métodos comuns incluem o método de compensação de dobras, o método de dedução de dobras e o método de cálculo do fator K. Esses métodos podem ajudar os projetistas a calcular o comprimento real do material no estado desdobrado, garantindo assim o tamanho esperado das peças após a dobra e a conformação finais.
Preste atenção ao manuseio de bordas e cantos e ao ajuste de detalhes: No processo de design de chapas metálicas, os detalhes do manuseio de bordas e cantos são muito importantes. Alguns softwares, como o SW, oferecem uma variedade de soluções de manuseio de bordas e cantos e métodos de dobra, o que ajuda a melhorar a precisão do desdobramento.
Para curvas que não sejam de 90 graus, os ângulos de curvatura comuns incluem, mas não se limitam a 45 graus e 135 graus. O método de cálculo do fator K baseia-se na relação entre a espessura do material e o raio da curva.
Especificamente, o fator K = δ / T, em que δ representa a espessura do material e T representa o raio de curvatura. Esse método é aplicável para calcular o coeficiente de curvatura de qualquer ângulo que não seja de 90 graus.
Em aplicações práticas, devido às possíveis diferenças e aos grandes erros nos valores de dedução de curvas em diferentes ângulos, o fator K é geralmente usado como coeficiente de curvatura.
Além disso, para orientar com precisão o valor do fator K de diferentes espessuras de chapa, são necessários ajustes. Algumas referências sugerem que o valor do fator K para qualquer raio de curvatura pode ser calculado por meio de técnicas específicas de interpolação, que se mostraram eficazes para aplicações industriais de chapas metálicas.
A fórmula de cálculo para o comprimento expandido da chapa metálica chanfrada do freio de prensa é: [L = A + B + C + 0,2], em que (A), (B) e (C) representam as dimensões internas e 0,2 serve como valor de compensação.
Com base nos princípios e práticas gerais dos cálculos de expansão de chapas metálicas, esse valor de compensação leva em conta as discrepâncias entre os comprimentos reais e os calculados teoricamente devido a fatores como flexão do material e erros de precisão do molde durante operações reais.
No processamento de chapas metálicas, esse valor de compensação ajuda a garantir a precisão dimensional e a qualidade do produto final.
As peças de chapa metálica são amplamente utilizadas nos setores eletromecânico, de indústria leve e automotivo.
A forma desdobrada das peças de chapa metálica é o principal fator determinante do tamanho do blank, que, por sua vez, afeta o tamanho e a forma do blank.
No entanto, os métodos tradicionais de desdobramento de peças de chapa metálica têm se tornado cada vez mais inadequados para atender às necessidades dos projetos modernos devido a seus longos ciclos, baixa eficiência e baixa qualidade.
Para resolver essas deficiências, o uso de sistemas CAD avançados tem se tornado cada vez mais predominante nos últimos anos.
Esses sistemas especializados de projeto de peças de chapa metálica apresentam funcionalidade robusta e podem reduzir bastante o tempo e o esforço necessários para o projeto preliminar e a implementação de peças de chapa metálica.