Como você mede a retidão de um trilho-guia para garantir operações precisas da máquina? Este artigo explora dois métodos comuns: o método de conexão de ponto de duas extremidades e o método de condição mínima. Ao comparar essas técnicas, você aprenderá como cada uma delas avalia os erros de retilinidade e por que a escolha do método correto é crucial para medições precisas. Mergulhe de cabeça para entender os prós e os contras de cada abordagem e descubra qual método atende melhor às suas necessidades para obter a retidão ideal em seus projetos de engenharia.
Na prática de engenharia, há dois métodos comumente usados para avaliar o erro de retidão dos trilhos de guia: o método de conexão de ponto de duas extremidades e o método de condição mínima.
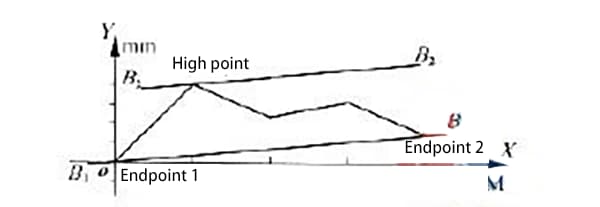
O método de conexão de ponto de duas extremidades conecta a curva de erro de ponta a ponta e, em seguida, desenha duas linhas paralelas à linha de ponta a ponta nos pontos mais altos e mais baixos da curva e mede os valores ao longo do eixo vertical entre as duas linhas paralelas.
Após o processamento dos dados, o valor é o erro de retidão do trilho-guia.
O método de condição mínima conecta os pontos "alto, alto" (ou "baixo, baixo") da curva de erro e desenha uma linha paralela a ela através do ponto baixo (alto).
O valor medido entre as duas linhas paralelas ao longo do eixo vertical é o erro de retidão do trilho-guia após o processamento dos dados.
O método de condição mínima é uma avaliação de arbitragem.
O método de conexão de dois pontos finais não é uma avaliação de arbitragem, mas é comumente usado na produção devido à sua simplicidade e conveniência na avaliação, embora às vezes possa produzir grandes erros.
Este artigo discute o valor limite do erro gerado entre esses dois métodos de avaliação.
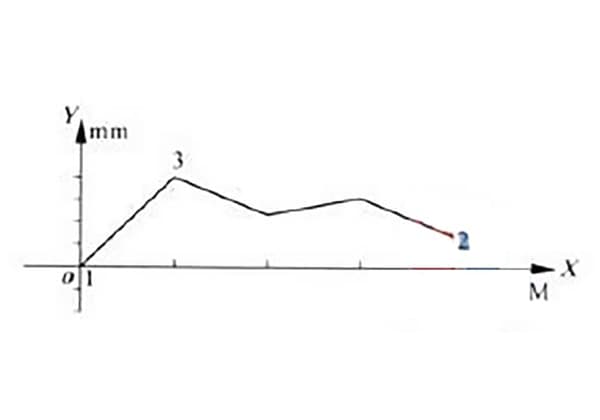
Medindo o erro de retidão de um determinado modelo de guia de trilho deslizante hidráulico, a curva de erro de retidão foi obtida conforme mostrado na Figura 1.
Como pode ser visto na figura, a curva de erro está no mesmo lado das duas extremidades da linha.
A seguir, o valor do erro de retidão do trilho-guia será avaliado usando o método de condição mínima e o método de conexão de duas extremidades.
(1) Avaliação do erro de linearidade usando o método de condição mínima
De acordo com o método da condição mínima, os pontos mais baixos 1 e 2 da curva da Figura 1 (com o ponto baixo 1 coincidindo com a origem) são conectados pela linha a1a1, conforme mostrado na Figura 2.
A reta paralela a2a2 é traçada através do ponto mais alto 3 em relação à reta a1a1.
O valor medido ao longo do eixo y na região delimitada pelas duas linhas paralelas a1a1 e a2a2, após o processamento dos dados, representa o erro de retilinearidade do trilho-guia δ obtido pelo método da condição mínima.
(2) Avaliação do erro de retidão usando o método de conexão de duas extremidades
De acordo com o método de conexão de duas extremidades, as extremidades da curva na Figura 1 também são os pontos finais 1 e 2 da curva, conforme mostrado na Figura 3.
Os pontos finais 1 e 2 são conectados pela linha b1b1 e, em seguida, uma linha paralela b2b2 é traçada através do ponto mais alto.
O valor medido ao longo do eixo y na região delimitada pelas duas linhas paralelas b1b1 e b2b2, após o processamento dos dados, representa o erro de retidão do trilho-guia δ obtido pelo método de conexão de duas extremidades.
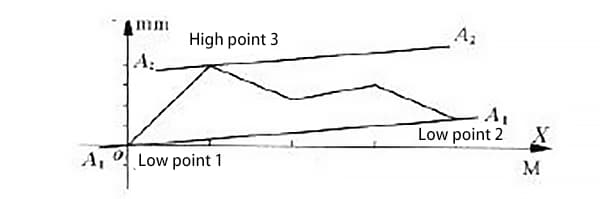
(3) Determinação do limite de erro gerado pelos dois métodos de avaliação
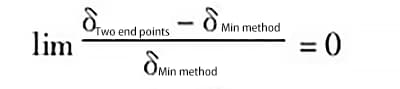
Como os dois métodos de avaliação são usados para determinar o erro de retidão do mesmo trilho-guia, o "ponto baixo 1", o "ponto baixo 2" e o "ponto alto 3" na Figura 2 correspondem, respectivamente, ao "ponto final 1", ao "ponto final 2" e ao "ponto alto 3" na Figura 3. Isso faz com que a linha a1a1 coincida com a linha b1b1 e a linha a2a2 coincida com a linha b2b2.
Portanto, o valor do erro gerado pelos dois métodos de avaliação é zero.
Com base na análise acima, quando a curva de erro está no mesmo lado de ambas as extremidades da linha, o limite de erro gerado pelos dois métodos de avaliação é zero, o que significa que os resultados de avaliação obtidos pelos dois métodos são os mesmos.
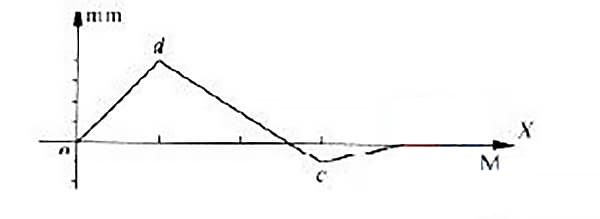
Na curva de erro de retidão medida de um trilho-guia, algumas curvas de erro estão em ambos os lados da linha que conecta as extremidades, conforme mostrado na Figura 4.
A curva de erro desse trilho-guia tem uma linha que liga suas extremidades e coincide com o eixo x. O erro de retidão do trilho-guia será avaliado usando o método de condição mínima e o método de conexão de duas extremidades.
Como pode ser visto na Figura 4, os pontos o e c são os dois pontos baixos e os dois pontos finais da curva, enquanto o ponto d é o ponto mais alto.
De acordo com o método da condição mínima, os pontos o e c são conectados pela linha a1a1, conforme mostrado na Figura 5. A linha a2a2 é traçada paralelamente à linha a1a1 passando pelo ponto mais alto d.
O valor medido ao longo do eixo y na região delimitada pelas duas linhas paralelas a1a1 e a2a2, após o processamento dos dados, representa o erro de retilinearidade do trilho-guia δ obtido pelo método da condição mínima.
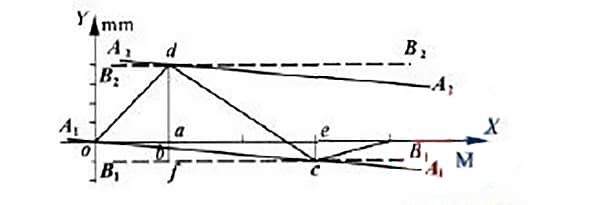
De acordo com o método de conexão de dois pontos, desenhe duas linhas paralelas ao eixo x passando pelos pontos C e D, respectivamente.
Essas linhas são representadas pelas linhas pontilhadas b1b1 e b2b2 na Figura 5. Na região delimitada por essas duas linhas paralelas, o valor medido ao longo do eixo y, após o processamento dos dados, representa o valor do erro de retilinearidade do trilho-guia entre os dois pontos finais.
Para determinar o método de desvio mínimo e o valor do desvio nos dois pontos finais, desenhe uma linha paralela ao eixo y passando pelo ponto D, cruzando o eixo no ponto A, cruzando a linha a1a1 no ponto H e cruzando a linha b1b1 no ponto F.
Da mesma forma, trace uma linha paralela ao eixo y que passe pelo ponto C e cruze o eixo no ponto E.
(1) Determinação do erro de retidão usando o método de condição mínima
De acordo com o método de condição mínima, o valor do erro de retidão δ do trilho-guia é derivado do valor medido ao longo do eixo y após o processamento de dados, o que representa o método de desvio mínimo.
Conforme mostrado na Figura 5:
E como BD = BA + AD,
Portanto, ∆OAB e ∆OEC são dois triângulos semelhantes,
Rearranjando a equação (3), obtemos:
Substituindo a equação (4) na equação (2) e reordenando, obtemos:
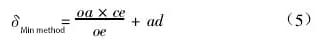
(2) Determinação do erro de retidão usando o método de conexão de dois pontos
De acordo com o método de conexão de dois pontos, o valor medido ao longo do eixo y após o processamento de dados representa o valor do erro de retidão δ do trilho-guia entre os dois pontos finais.
Conforme mostrado na Figura 5:
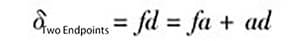
E como fa = ce,
(3) Cálculo dos valores de erro gerados por dois métodos de avaliação
Equação (6) menos a equação (5), ou seja
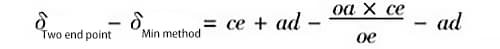
Rearranjando, obtemos:
(4) Cálculo do erro máximo gerado por dois métodos de avaliação
Na Figura 5, deixe ad = δ1, ce = δ2, oa = p; deixe o comprimento do trilho-guia que está sendo medido ser l, então oe = l - p e:
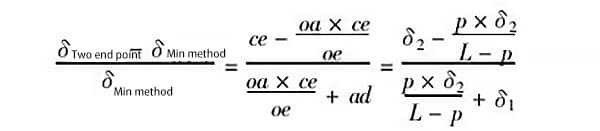
Por exemplo, quando p = 0,5 m (ou seja, o passo é de 0,5 m), δ1 = 1,0δ, δ2 = 0,25δ e o comprimento do trilho-guia medido é l - 2 m, então a proporção de erro gerada pelos dois métodos de avaliação é:
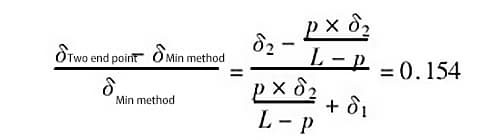
A proporção de erro gerada pelos dois métodos de avaliação é de 0,154, o que significa que o erro gerado pelo método de conexão de dois pontos é 15,4% maior do que o gerado pelo método de condição mínima.
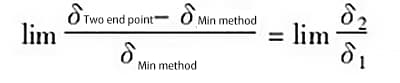
Na equação acima, quando 
ou seja, os pontos mais alto e mais baixo da curva de erro estão infinitamente distantes, então
, de modo que obtemos:
Por exemplo, quando δ1 = 1,0δ e δ2 = 0,25δ e a distância entre os pontos mais alto e mais baixo da curva de erro é infinitamente distante (ou seja, L=0,25), então a proporção de erro gerada pelos dois métodos de avaliação é 
o que significa que o erro gerado pelo método de conexão de dois pontos é 25% maior do que o erro gerado pelo método de condição mínima.
Quando δ1 = δ2, ou seja, a distância entre os pontos mais alto e mais baixo da curva de erro é igual, conforme mostrado na Figura 6, os valores máximos de erro gerados pelos dois métodos de avaliação são:
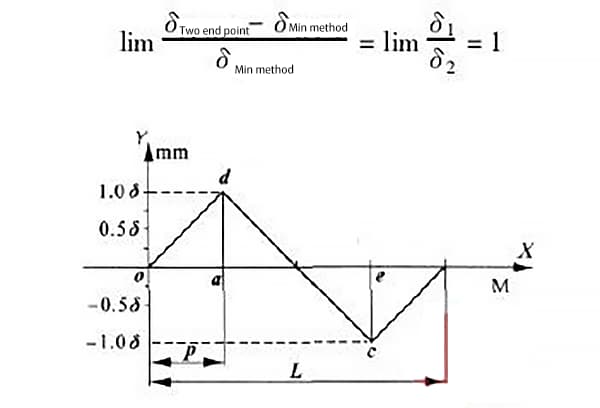
A partir disso, pode-se observar que, quando os pontos mais alto e mais baixo do trilho-guia são iguais e infinitamente distantes, o erro máximo gerado pelos dois métodos de avaliação é o maior e pode chegar a 100%.
A Tabela 1 lista a proporção de erros gerados pelos dois métodos de avaliação para diferentes comprimentos do trilho-guia medido, quando os pontos da curva de erro são distribuídos em ambos os lados da linha de conexão de dois pontos.
A distância entre os pontos mais alto e mais baixo da curva de erro é igual quando o passo de medição p = 0,5.
Tabela 1 Taxa de erro de dois métodos de avaliação
| Taxa de erro | Distância L (M) entre os pontos mais alto e mais baixo do trilho-guia | ||||||
| 1 | 10 | 15 | 20 | 25 | 30 | 40 | ∞ |
 | 33.30% | 90% | 93.30% | 95% | 96% | 96.70% | 97.50% |
Se os pontos da curva de erro de retidão estiverem no mesmo lado da linha de conexão de dois pontos, os erros gerados pelos dois métodos de avaliação serão zero, ou seja, os resultados obtidos pelos dois métodos de avaliação serão os mesmos.
Se os pontos da curva de erro de retidão estiverem em ambos os lados da linha de conexão de dois pontos, e os pontos mais altos e mais baixos da curva de erro forem iguais e infinitamente distantes, o erro máximo gerado pelos dois métodos de avaliação será o maior, e o erro gerado pelo método de conexão de dois pontos poderá ser 100% maior do que o gerado pelo método de condição mínima.
Portanto, ao avaliar o erro de retidão de trilhos-guia de máquinas-ferramenta grandes na produção prática, é muito importante escolher o método de avaliação adequado. Quando os pontos da curva de erro estão em ambos os lados da linha de conexão de dois pontos, o método de condição mínima deve ser usado como a primeira opção de avaliação.
Como fundador do MachineMFG, dediquei mais de uma década de minha carreira ao setor de metalurgia. Minha vasta experiência permitiu que eu me tornasse um especialista nas áreas de fabricação de chapas metálicas, usinagem, engenharia mecânica e máquinas-ferramentas para metais. Estou sempre pensando, lendo e escrevendo sobre esses assuntos, esforçando-me constantemente para permanecer na vanguarda do meu campo. Permita que meu conhecimento e experiência sejam um trunfo para sua empresa.
PT_BR 
EN 
AR 
DE 
ES 
FR 
IT 
JA 
NL 
PT 
RU 
KO