Imagine estar em uma ponte e ver um caminhão pesado passar. Já se perguntou por que a ponte não desmorona sob o peso? Este artigo se aprofunda nos conceitos de deformação e estresse, explicando como os materiais se deformam sob força e como os engenheiros calculam essas deformações para garantir a segurança. Você aprenderá as relações fundamentais entre essas forças, como elas são medidas e suas implicações práticas nas estruturas cotidianas. Seja você um engenheiro iniciante ou apenas um curioso, este guia lançará luz sobre as forças invisíveis que mantêm nosso mundo intacto.

Em primeiro lugar, a maior parte do setor de monitoramento de segurança consiste em medir a deformação da estrutura que está sendo testada. Uma deformação excessiva pode causar acidentes.
Por exemplo, rachaduras em estruturas, afundamento e deslocamento entre a estrutura e uma referência fixa são deformações grandes que podem ser vistas a olho nu e podem ser medidas em milímetros usando medidores como medidores de rachaduras, níveis estáticos e medidores de deslocamento.
Mas como pode ser representada a pequena deformação causada pela compressão dentro da estrutura que está sendo testada ou pela flexão fora do objeto em forma de viga?
A resposta é a tensão.

Suponha que o comprimento de uma estrutura com comprimento L sofra deformação sob tensão e seu comprimento mude para L', então sua mudança no comprimento ΔL = L' - L, e a deformação ε é a proporção da mudança no comprimento ΔL em relação ao comprimento original L, a fórmula é a seguinte:

Então, qual é a unidade de tensão?
Como pode ser visto na fórmula, a deformação é uma proporção e não tem dimensão, ou seja, não tem unidade.
Então, o que é microstrain?
Como ΔL é muito pequeno, geralmente na faixa de mícrons, o valor da deformação calculada é muito pequeno, com muitas casas decimais, o que torna inconveniente a exibição e a visualização, de modo que foi introduzida a notação científica 10-6, chamada de microstrain με, que pode ser entendida como a unidade de microstrain é 10-6, e nossa faixa de medição de strain gauge é de ±1500 microstrains, sendo que o positivo indica alongamento e o negativo indica compressão.
A deformação é uma pequena deformação dentro da estrutura que está sendo testada, então por que ela se deforma? Porque ela é submetida a uma força externa.
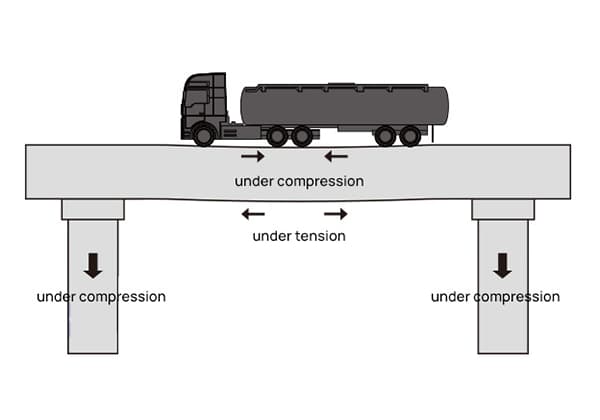
Tomando um píer de ponte como exemplo, se um caminhão totalmente carregado passar sobre a ponte, o píer sofrerá pressão adicional e produzirá compressão e deformação por compressão, enquanto o píer produzirá uma força interna para neutralizar a força externa e superar a deformação.
Essa força interna é o estresse. O estresse é definido como a força por unidade de área, que na verdade é a pressão, com unidades de MPa.
Então, qual é a relação entre a variável de deformação e a mudança na tensão que é suportada? Veja a fórmula de cálculo:

Na fórmula, σ representa a tensão, E é o módulo de elasticidade do material que está sendo testado, também conhecido como módulo de Young, que é uma quantidade física que descreve a elasticidade do material.
Ela pode ser vista como a capacidade do material de resistir à deformação (rigidez) e, de uma perspectiva micro, é a força de ligação entre átomos e moléculas.
Dois materiais com a mesma deformação (o mesmo valor de deformação), o material com maior resistência à deformação (um módulo de elasticidade maior) suportará uma tensão maior.
Por exemplo, o tofu e o bloco de ferro do mesmo tamanho, se sua altura for comprimida em 1 mm, o primeiro só precisa ser pressionado suavemente com a mão, enquanto o segundo deve ser auxiliado por uma ferramenta.
O módulo de elasticidade dos materiais de engenharia comuns pode ser encontrado em tabelas, como, por exemplo, o módulo de elasticidade do concreto C30 é 30000MPa (1N/mm2 = 1MPa), e o módulo de elasticidade do aço carbono é de 206GPa.
O módulo de elasticidade Ec do concreto sob compressão e tensão deve ser adotado de acordo com a Tabela 4.1.5.
O módulo de deformação de cisalhamento Gc do concreto pode ser adotado como 40% do valor do módulo de elasticidade correspondente.
O coeficiente de Poisson Vc do concreto pode ser adotado como 0,2.
Tabela4.15 Módulo de elasticidade do concreto (×104N/mm2).
| Grau de resistência do concreto | C15 | C20 | C25 | C30 | C35 | C40 | C45 | C50 | C55 | C60 | C65 | C70 | C75 | C80 |
| Ec | 2.20 | 2.55 | 2.80 | 3.00 | 3.15 | 3.25 | 3.35 | 3.45 | 3.55 | 3.60 | 3.65 | 3.70 | 3.75 | 3.80 |
Observação:
1. Quando há dados de teste confiáveis disponíveis, o módulo de elasticidade pode ser determinado com base nos dados reais medidos;
2. Quando uma grande quantidade de aditivos minerais é adicionada ao concreto, o módulo de elasticidade pode ser determinado com base em dados reais medidos de acordo com a idade especificada.
Tabela 1.1-13 Módulo elástico e coeficiente de Poisson de materiais comumente usados
| Item | Módulo elástico E/GPa | Módulo de cisalhamento G/GPa | Índice de Poisson μ | Item | Módulo elástico E/GPa | Módulo de cisalhamento G/GPa | Teflon |
| Ferro fundido cinza | 118~126 | 44.3 | 0.3 | Zinco laminado | 82 | 31.4 | 0.27 |
| Ferro fundido nodular | 173 | 0.3 | Liderança | 16 | 6.8 | 0.42 | |
| Aço carbono, aço níquel-cromo | 206 | 79.4 | 0.3 | Vidro | 55 | 1.96 | 0.25 |
| Liga de aço | Vidro orgânico | 2.35-29.42 | |||||
| Aço fundido | 202 | 0.3 | Borracha | 0.0078 | 0.47 | ||
| Cobre puro laminado | 108 | 39.2 | 0.31-0.34 | Baquelite | 1.96-2.94 | 0.69-2.06 | 0.35-0.38 |
| Cobre puro estirado a frio | 127 | 48.0 | Plástico fenólico sanduíche | 3.92-8.83 | |||
| Bronze de fósforo e estanho laminado | 113 | 41.2 | 0.32-0.35 | Celuloide | 1.71-1.89 | 0.69-0.98 | 0.4 |
| Latão trefilado a frio | 89-97 | 34.3-36.3 | 0.32-0.42 | Nylon 1010 | 1.07 | ||
| Bronze manganês laminado | 108 | 39.2 | 0.35 | Cloreto de polivinila não plastificado | 3.14-3.92 | 0.35-0.38 | |
| Alumínio laminado | 68 | 25.5-26.5 | 0.32-0.36 | Teflon | 1.14-1.42 | ||
| Fio de alumínio trefilado | 69 | Polietileno de baixa pressão | 0.54-0.75 | ||||
| Alumínio fundido bronze | 103 | 41.1 | 0.3 | Polietileno de alta pressão | 0.147-0.245 | ||
| Bronze de estanho fundido | 103 | 0.3 | concreto | 13.73~39.2 | |||
| Liga de duralumínio | 70 | 26.5 | 0.3 | 4.9-15.69 | 0.1-0.18 |
Afinal, quando as tensões internas não podem ser medidas diretamente, a tensão pode ser calculada medindo-se a deformação e, em seguida, multiplicando-a pelo módulo de elasticidade do material