Neste artigo, exploramos os fascinantes conceitos de resistência e rigidez na engenharia. Você aprenderá como esses princípios garantem a segurança e a durabilidade de objetos do cotidiano, de pontes a telas de smartphones. Junte-se a nós para descobrir os segredos por trás das maravilhas da engenharia!
Para garantir o desempenho e a confiabilidade ideais de um sistema ou estrutura mecânica, cada componente deve cumprir a função pretendida de forma eficaz e eficiente. O principal objetivo do projeto de segurança de componentes de engenharia é garantir que todos os elementos tenham resistência, rigidez e estabilidade adequadas, assegurando assim a integridade geral e a longevidade do sistema.
A estabilidade é um conceito fundamental na engenharia, referindo-se à capacidade de um componente de manter ou recuperar seu estado de equilíbrio original quando submetido a forças externas. Esse princípio é fundamental em vários cenários, como, por exemplo:
Esses exemplos ilustram a importância da estabilidade para evitar falhas catastróficas e garantir a operação segura de sistemas e estruturas mecânicas.
Nesta discussão, vou me concentrar em elucidar minha compreensão abrangente de dois princípios de engenharia igualmente cruciais: rigidez e resistência. Esses conceitos, juntamente com a estabilidade, formam a tríade de considerações fundamentais no projeto de segurança de componentes, cada um desempenhando um papel vital na determinação do desempenho geral, da durabilidade e da segurança dos sistemas projetados.
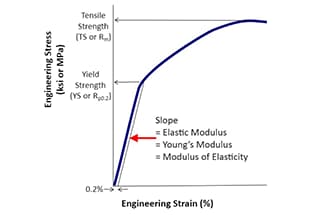
Definição: Resistência é a capacidade de materiais, componentes ou estruturas de suportar cargas ou forças aplicadas sem falhas, deformações excessivas ou danos. É uma propriedade fundamental na ciência e engenharia de materiais que determina a capacidade de um material de resistir ao estresse mecânico.
A força abrange vários aspectos, inclusive:
Por exemplo, na fabricação de metais, compreender a resistência dos materiais é fundamental para projetar componentes que possam suportar cargas operacionais. Uma viga de aço em um edifício deve ter resistência suficiente para suportar o peso da estrutura e cargas adicionais sem dobrar ou quebrar.
A força é influenciada por vários fatores, inclusive:
A unidade de medida de resistência é normalmente expressa em megapascal (MPa) ou libras por polegada quadrada (psi) em unidades imperiais. Por exemplo, o aço doce tem uma resistência à tração de aproximadamente 400-550 MPa, enquanto os aços de liga de alta resistência podem exceder 1000 MPa.
Na fabricação e na engenharia, os cálculos e testes de resistência são essenciais para:
Técnicas avançadas, como a análise de elementos finitos (FEA) e testes destrutivos, são frequentemente empregadas para avaliar e validar a resistência de materiais e componentes em aplicações complexas de engenharia.
Fratura frágil: Um modo de falha repentino e catastrófico caracterizado pela rápida propagação de rachaduras com deformação plástica mínima. Esse tipo de falha ocorre sem aviso e normalmente resulta em uma superfície de fratura limpa e plana.
Por exemplo:
Rendimento do plástico: Um modo de falha em que o material sofre deformação plástica significativa, resultando em mudança permanente de forma e perda de integridade estrutural. Esse tipo de falha geralmente é mais gradual e observável em comparação com a fratura frágil.
Por exemplo:
É importante observar que o modo de falha de um material depende de vários fatores, incluindo propriedades do material, condições de carga, temperatura e fatores ambientais. Alguns materiais podem apresentar uma transição de comportamento dúctil para frágil sob determinadas condições, como baixas temperaturas ou altas taxas de deformação.
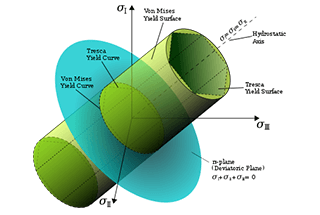
1. Teoria da tensão máxima de tração:
Quando a tensão máxima de tração σ1 em um ponto do membro atingir a tensão máxima σb sob condições de tensão unidirecional, o material sofrerá fratura frágil. Assim, os critérios para a falha de fratura frágil de componentes com pontos críticos sob condições de tensão complexas são: σ1 = σb.
Consequentemente, as condições de resistência estabelecidas pelo primeiro teoria da força são: σ1 ≤ σb.
2. Teoria da tensão máxima de tração:
Quando a deformação máxima de tração ε1 atingir o valor limite εu sob condições de tensão unidirecional, o material falhará devido à fratura frágil. Isso pode ser expresso como ε1 = εu.
A partir da Lei de Hooke generalizada, podemos calcular ε1 como: ε1 = [σ1 - u(σ2 + σ3)] / E, de modo que σ1 - u(σ2 + σ3) = σb.
As condições de resistência estabelecidas pela segunda teoria de resistência são: σ1 - u(σ2 + σ3) ≤ σb.
3. Teoria da tensão de cisalhamento máxima:
Quando a tensão de cisalhamento máxima τMax atingir a tensão de cisalhamento máxima τ0 sob condições de tensão unidirecional, o material falhará devido ao escoamento. Isso pode ser expresso como τMax = τ0.
A fórmula para a tensão de cisalhamento em uma seção inclinada durante a tensão axial é τ0 = σs/2 (σs é a tensão normal na seção transversal). A fórmula para τMax é (σ1 - σ3)/2. Assim, a condição de dano pode ser reescrita como σ1 - σ3 = σs.
A condição de resistência estabelecida pela terceira teoria de resistência é: σ1 - σ3 ≤ σs.
4. Teoria da energia específica de mudança de forma:
Quando a taxa de mudança de forma em um ponto do membro atingir o valor limite sob condições de tensão unidirecional, o material falhará devido à deformação.
A condição de resistência estabelecida pela quarta teoria de resistência é:
√(σ1^2 + σ2^2 + σ3^2 - σ1σ2 - σ2σ3 - σ3σ1) < σs.
Definição: A rigidez refere-se à capacidade de um material, componente ou estrutura de resistir à deformação elástica ou ao deslocamento quando submetido a uma força externa. Ela quantifica a extensão em que um sistema pode manter sua forma e dimensões dentro dos limites permitidos sob cargas aplicadas.
A rigidez é um parâmetro fundamental na engenharia que caracteriza a relação entre força e deformação em um material ou estrutura. Ela é definida como a relação entre a força aplicada e o deslocamento resultante, indicando a quantidade de força necessária para produzir uma unidade de deformação. Em termos matemáticos, a rigidez (k) é expressa como:
k = F / δ
Onde:
A unidade de rigidez é normalmente a força por unidade de comprimento, como N/m (Newtons por metro) no sistema SI ou lbf/in (libras-força por polegada) no sistema imperial.
Em termos práticos, a rigidez pode ser conceituada usando a analogia de uma mola. A constante da mola, que representa a rigidez de uma mola, é definida como a razão entre a força de tração ou compressão aplicada e o alongamento ou a compressão resultante. Essa relação é descrita pela Lei de Hooke para sistemas elásticos lineares.
Compreender e controlar a rigidez é fundamental em várias aplicações de engenharia, inclusive:
Os engenheiros precisam equilibrar os requisitos de rigidez com outras considerações de projeto, como resistência, peso, custo e capacidade de fabricação, para criar soluções ideais para aplicações específicas.
Quando a carga aplicada é constante, ela é chamada de rigidez estática.
Quando a carga se alterna, isso é chamado de rigidez dinâmica.
A rigidez estática engloba a rigidez estrutural e a rigidez de contato.
A rigidez estrutural refere-se à rigidez do próprio membro e inclui a rigidez de flexão e a rigidez de torção.
1. Rigidez à flexão: calculada de acordo com a seguinte fórmula:
K=P/δ
Onde
2. A rigidez de torção é calculada de acordo com a seguinte fórmula:
Km=ML/θ
Onde M - torque aplicado (n - m);
L - distância da posição de ação do torque até a extremidade fixa (m);
θ-- Ângulo de torção (°)
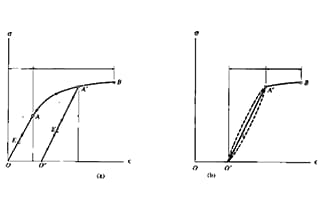
A partir da explicação acima sobre resistência e rigidez, pode-se observar que a resistência se concentra na falha sob força externa e é classificada em falha de rendimento plástico e fratura frágil, que está relacionada à curva de tensão-deformação durante o teste de tração. Em comparação, a rigidez diz respeito à relação entre deformação e força.
Conforme mostrado na fig.
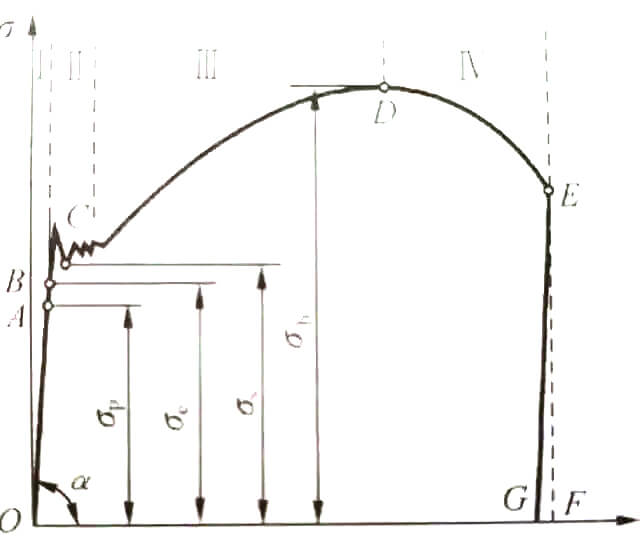
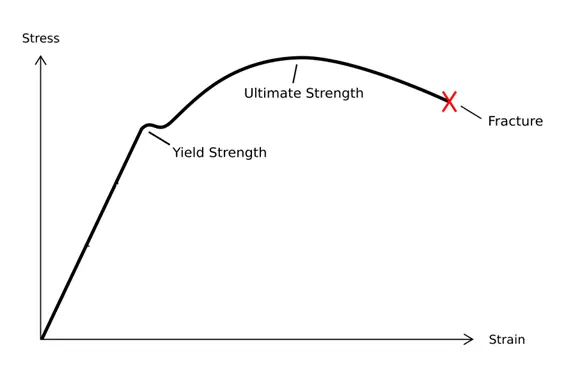
A curva da figura pode ser dividida em quatro estágios:
1. Estágio de deformação elástica;
2. Estágio de rendimento;
3. Estágio de fortalecimento;
4. Estágio de necking local.
A rigidez é definida como a resistência à deformação elástica, que ocorre no estágio inicial e é regida pela lei de Hooke sob condições elásticas.
Cálculo da rigidez de flexão e da rigidez de torção sob cargas estáticas é semelhante à lei de Hooke, sugerindo que a rigidez só é medida durante o estágio de deformação elástica.
No estágio seguinte, quando ocorre a deformação plástica durante o teste de tração, a deformação residual não desaparece. Na curva de tensão-deformação, embora a tensão permaneça quase inalterada, a deformação aumenta significativamente. Nesse ponto, a tensão atinge o limite de rendimento e o material entra no estágio de falha de rendimento plástico. À medida que a tensão continua a aumentar, a deformação também aumenta até atingir o limite de resistência.
Portanto, a medição da resistência ocorre depois que o material sofre deformação elástica e antes de atingir o limite de resistência.
Concluindo, a rigidez e a resistência são avaliadas durante o estágio de falha das peças, com a rigidez sendo medida pela tensão e a resistência sendo medida pela deformação.
Em termos de sua ordem no processo de deformação, a rigidez ocorre no estágio inicial, enquanto a resistência ocorre no estágio posterior.
Portanto, ao avaliar as condições de falha das peças, desde que os requisitos de rigidez sejam atendidos, a peça deve ser capaz de suportar tensão suficiente durante o estágio de deformação elástica, o que, por sua vez, deve atender aos requisitos de resistência.
Essa relação se reflete em vários projetos, como o eixo de equipamentos mecânicos. Normalmente, o tamanho do eixo é determinado com base nas condições de resistência e, em seguida, sua rigidez é verificada com base nas condições de rigidez.
Portanto, os requisitos de rigidez para eixos de máquinas de precisão são muito altos, e o projeto de seu tamanho de seção transversal é frequentemente controlado pelas condições de rigidez.
Como fundador do MachineMFG, dediquei mais de uma década de minha carreira ao setor de metalurgia. Minha vasta experiência permitiu que eu me tornasse um especialista nas áreas de fabricação de chapas metálicas, usinagem, engenharia mecânica e máquinas-ferramentas para metais. Estou sempre pensando, lendo e escrevendo sobre esses assuntos, esforçando-me constantemente para permanecer na vanguarda do meu campo. Permita que meu conhecimento e experiência sejam um trunfo para sua empresa.
PT_BR 
EN 
AR 
DE 
ES 
FR 
IT 
JA 
NL 
PT 
RU 
KO