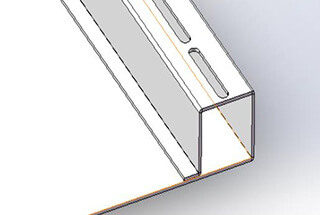
Вы когда-нибудь задумывались, почему ваши проекты из листового металла не всегда идеально подходят друг к другу? Ключ к разгадке кроется в понимании припусков на изгиб. Эта концепция обеспечивает точную гибку и сокращает отходы материала. В этой статье вы узнаете, как освоить припуск на изгиб в SOLIDWORKS, чтобы сделать ваши проекты точными и эффективными. Приготовьтесь изменить свой процесс изготовления листового металла!
Понятие о припуске на изгиб
Припуск на изгиб - важнейший параметр при изготовлении листового металла, определяющий точную плоскую длину материала, необходимую для получения требуемых размеров после гибки. Он представляет собой длину дуги изгиба, измеренную вдоль нейтральной оси материала - воображаемой линии в области изгиба, где материал не растягивается и не сжимается в процессе гибки.
На расчет припуска на изгиб влияет множество факторов, включая толщину листового металла, радиус изгиба, свойства материала и угол изгиба. В SOLIDWORKS пользователи могут определять значения припусков на изгиб и манипулировать ими, чтобы осуществлять точный контроль над разработкой деталей из листового металла, обеспечивая точность как на этапе проектирования, так и на этапе производства.
Значение припуска на изгиб
Точный расчет и применение припусков на изгиб необходимы для производства точно согнутых деталей из листового металла. Это обеспечивает соответствие разработанного (плоского) размера детали проектному замыслу и гарантирует, что изгибы будут выполнены под правильными углами и в правильном положении. Такая точность значительно снижает количество ошибок, отходов материала и переделок в процессе изготовления, что в конечном итоге повышает эффективность производства и рентабельность.
Понимание и применение соответствующих значений припусков на изгиб позволяет проектировщикам и изготовителям:
В SOLIDWORKS правильное использование припусков на изгиб способствует более точному моделированию, упрощает переход от проектирования к производству и позволяет создавать более сложные и точные детали из листового металла. Это также позволяет улучшить интеграцию с гибочными станками с ЧПУ и другими автоматизированными производственными процессами, что еще больше повышает производственные возможности и согласованность.
Свойства материала
Свойства материалов существенно влияют на расчеты припусков на изгиб в SolidWorks. Каждый металл обладает уникальными характеристиками упругой и пластической деформации, что напрямую влияет на его поведение при изгибе. Например, алюминиевые сплавы обычно имеют более низкий предел текучести и более высокую упругость по сравнению со сталью, что приводит к различным эффектам пружинения и значениям припусков на изгиб. Марки нержавеющей стали, известные своими упрочняющими свойствами, требуют тщательного рассмотрения для предотвращения чрезмерного или недостаточного изгиба. Модуль Юнга, предел текучести и коэффициент деформационного упрочнения материала - важнейшие параметры, которые используются в SolidWorks для точного определения припусков на изгиб.
Угол изгиба
Угол изгиба является критическим фактором при расчете припусков на изгиб. С увеличением угла припуск на изгиб обычно увеличивается нелинейно из-за сложного соотношения напряжений и деформаций в материале. Например, 90-градусный изгиб обычно требует большего припуска, чем 45-градусный, но не в два раза больше. В SolidWorks используются усовершенствованные алгоритмы, которые учитывают эту нелинейную зависимость, принимая во внимание такие факторы, как смещение нейтральной оси и утончение материала на изгибе. Программное обеспечение позволяет конструкторам точно настраивать углы изгиба и автоматически пересчитывать припуски, обеспечивая точность сложных узлов из листового металла.
Толщина материала
Толщина материала играет ключевую роль при определении припусков на изгиб. Более толстые материалы не только требуют больших припусков на изгиб, но и демонстрируют более сложное поведение при изгибе. С увеличением толщины смещается положение нейтральной оси, что влияет на общую геометрию изгиба. SolidWorks включает в себя сложные модели, которые учитывают это смещение, обеспечивая точные расчеты припусков в широком диапазоне толщин. Кроме того, программное обеспечение учитывает коэффициент k (коэффициент, отражающий расположение нейтральной оси), который зависит от толщины материала и метода изгиба. Это позволяет точно моделировать тонкие материалы, используемые в корпусах электроники, а также толстые листы, применяемые в компонентах тяжелого оборудования.
Bend Deduction, или BD, - это терминология, используемая в производство листового металла. Она представляет собой разницу между припуском на изгиб и удвоенным внешним отступом в материале. Эта величина является ключевым фактором при определении общей плоской длины деталей из листового металла в процессе гибки. Она помогает изготовителям создавать точные детали из листового металла, которые соответствуют требуемым размерам.
При работе в SOLIDWORKS конструкторы могут выбирать между значениями припусков на изгиб и вычетов на изгиб в своих конструкциях из листового металла. Оба варианта полезны для определения окончательной плоской формы детали из листового металла и необходимы для точного изготовления.
Припуск на изгиб это длина дуги изгиба, измеренная вдоль нейтральной оси материала. Она представляет собой длину металлического листа, растягиваемого или сжимаемого в процессе гибки. Нейтральная ось относится к области в материале, где нет напряжения или деформации.
| Параметр | Описание |
|---|---|
| Допуск на изгиб | Длина дуги изгиба вдоль нейтральной оси материала |
| Вычет за изгиб | Разница между припуском на изгиб и удвоенным внешним отступом |
| BD | Аббревиатура вычета за изгиб |
При использовании SOLIDWORKS важно ввести правильное значение припуска на изгиб или вычета на изгиб, в зависимости от выбранного метода. Это гарантирует, что конечная деталь из листового металла будет иметь нужные размеры и правильно вписываться в сборки.
Оба метода имеют свои преимущества и особенности. Расчеты припусков на изгиб дают более точное представление о процессе гибки и учитывают поведение материала при изгибе. Вычет на изгиб упрощает процесс расчета и более понятен для новичков. конструкция из листового металла.
В заключение следует отметить, что понимание различий между припусками на изгиб и вычетами на изгиб имеет решающее значение для точного проектирования листового металла в SOLIDWORKS. Точный ввод этих значений гарантирует, что конечный компонент из листового металла будет соответствовать проектным спецификациям и органично впишется в требуемую сборку.
Вы можете напрямую использовать наш Калькулятор припусков на изгиб для расчета припуска на изгиб. Кроме того, калькулятор изготовления также поможет вам рассчитать коэффициент K, коэффициент Y, припуск на изгиб, вычет за изгиб, и т.д.
Вам может быть интересно, что такое припуск на изгиб, если вы никогда не работали с листовой металл до.
Когда лист сгибается в листогибочный прессПри этом часть листа, находящаяся рядом с пуансоном и соприкасающаяся с ним, удлиняется, компенсируя данный изгиб.
Если вы сравните длину этой части до и после сгибания, то увидите, что они разные.
Как инженер, если вы не компенсируете это отклонение, конечный продукт не будет иметь точных размеров.
Это особенно важно для деталей, где требуется соблюсти более жесткий припуск или точность.
В этой статье я расскажу о некоторых основных проблемах и принципах, с которыми вам придется регулярно сталкиваться при работе с листовым металлом.
Прежде чем мы начнем, я хочу кое-что прокомментировать: на самом деле не существует научного метода или формулы для определения точного расчета припуска на изгиб, потому что в процессе производства детали из листового металла действует множество факторов.
Например, фактическая толщина материала, бесконечное множество условий работы инструмента, методы формованияи так далее.
Здесь много переменных, и в реальности для расчета припуска на изгиб используется множество методов.
Метод проб и ошибок является, пожалуй, самым популярным, в то время как таблицы изгибов - еще одна часто используемая техника.
Таблицы изгибов обычно можно найти у поставщиков металла, производителей и в учебниках по машиностроению. Некоторые компании разрабатывают собственные таблицы изгибов на основе своих стандартных формул.
Теперь вернемся к Solidworks. Как именно Solidworks рассчитывает припуск на изгиб? Solidworks использует два метода: припуск на изгиб и вычет на изгиб.
Я расскажу, что это за методы, и покажу, как они используются в Solidworks.
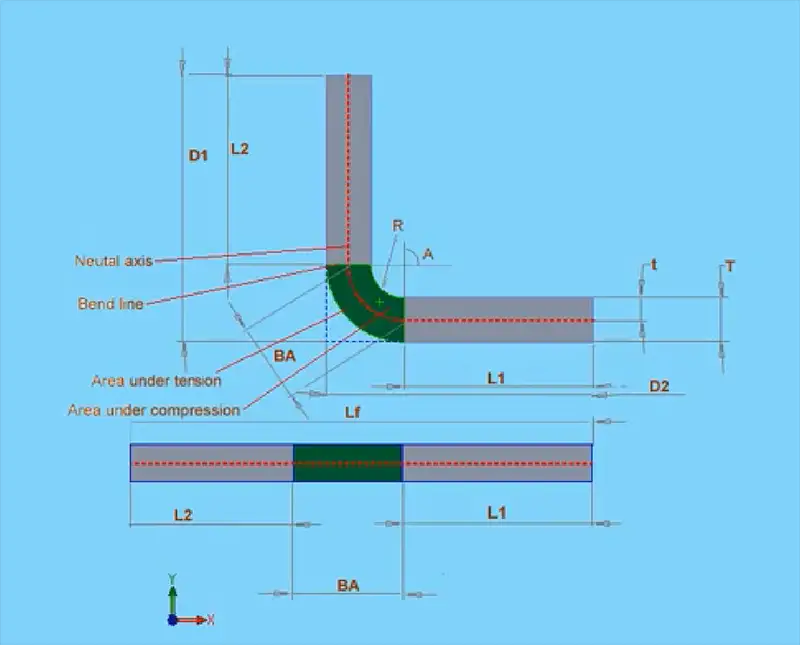
Метод припуска на изгиб основан на формуле, которая показана на моей диаграмме.
Общая длина сплющенного листа равна сумме L1 (первая длина), L2 и припуска на изгиб.
Область припуска на изгиб показана на моей диаграмме зеленым цветом. Именно в этой области происходит вся деформация в процессе изгиба.
Как правило, припуск на изгиб будет различным для каждого сочетания типа материала, толщины материала, радиус изгибаугол изгиба, а также различные процессы обработки, типы, скорости и т.д. Список возможных переменных обширен.
Значения припусков на изгиб, которые дают поставщики листового металла, производители и учебники по машиностроению, представлены в таблицах изгибов. Таблица изгибов выглядит как следующая электронная таблица Excel.
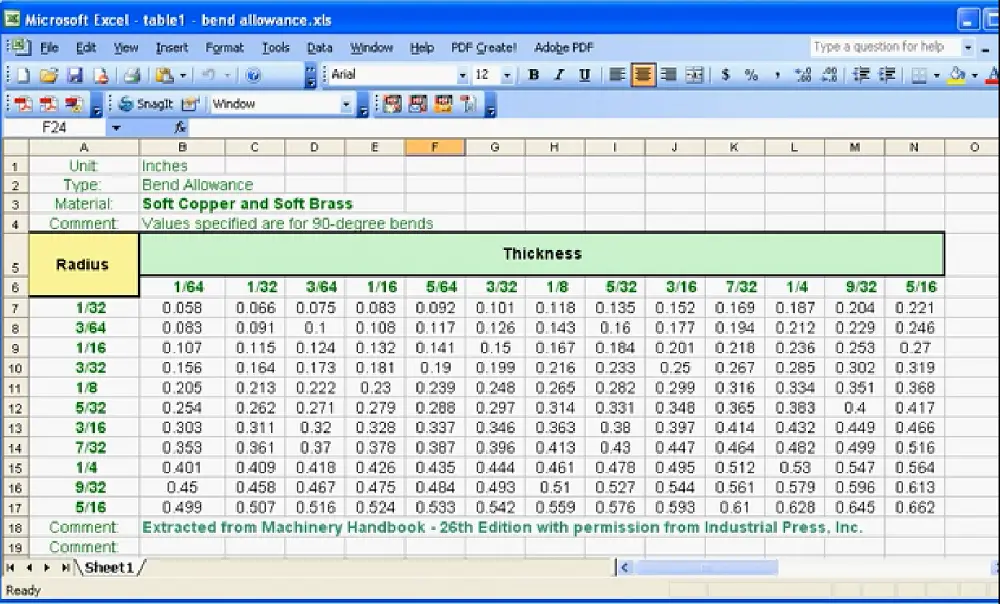
Метод таблицы изгибов, вероятно, является наиболее точным методом расчета припусков на изгиб.
Вы можете вручную ввести данные в матрицу угла изгиба и радиус изгиба. Если вы не уверены в величине припуска на изгиб, можно провести несколько тестов.
Вам понадобится кусок точно такого же листового металла, который вы будете использовать для изготовления детали, а затем вы согнете его с помощью тех же процессов, которые вы будете использовать во время обработки. Просто сделайте несколько измерений до и после гибки, и на основе этой информации вы сможете отрегулировать необходимый припуск на изгиб.
Еще один метод, который использует Solidworks, - это метод вычитания изгиба.
Формула выглядит следующим образом:
Длина деталей в расправленном виде, Lf, равна D1 плюс D2 минус вычет на изгиб.
Как и припуски на изгиб, вычеты на изгиб берутся из тех же источников: таблиц и ручного тестирования.
Как видите, легко понять, как эти величины связаны друг с другом, основываясь на информации, представленной в этих формулах.
Другой метод расчета припусков на изгиб использует коэффициент K.
K представляет собой смещение нейтральной оси.
Общий принцип этой формулы таков: нейтральная ось (показана красным на моей диаграмме) не меняется в течение процесс гибки. В процессе гибки материал внутри нейтральной оси будет сжиматься, а материал вне нейтральной оси - растягиваться. Нейтральная ось будет находиться ближе к внутреннему изгибу (обозначен синим цветом на диаграмме). Чем сильнее изгибается деталь, тем ближе нейтральная ось будет находиться к внутренней части детали.
Формула расчета припуска на изгиб с учетом коэффициента K приведена ниже:
BA = 2πA(R+KT)/360
Коэффициент K равен t - расстоянию смещения до нейтральной оси, деленному на большую T - толщину материала.
В этой формуле припуск на изгиб равен 2 умножить на пи, умножить на A (угол), умножить на сумму R (радиус изгиба) и коэффициента K, умножить на T (толщину материала). Затем разделите все это на 360.
Теоретически коэффициент K может быть в любом диапазоне от 0 до 1, но для практических целей он обычно составляет от 0,25 до 0,5.
Например, твердые материалы, такие как сталь, имеют более высокий коэффициент K, например 0,5, в то время как мягкие материалы, такие как медь или латунь, имеют более низкий коэффициент K, близкий к 0.
И не волнуйтесь, это последняя формула, которую мы рассмотрим в этом уроке. Сейчас она может показаться немного запутанной, но с некоторой практикой она станет второй натурой.
И последнее: давайте посмотрим на пример. На этой части есть подол, который имеет коэффициент K около 0,3. С другой стороны, мягкий изгиб, такой как постепенный изгиб на другой стороне этой детали, имеет более высокий коэффициент K - около 0,5. На этом мы завершаем наш урок по припускам на изгиб.
Дальнейшее чтение:
Как основатель MachineMFG, я посвятил более десяти лет своей карьеры металлообрабатывающей промышленности. Мой обширный опыт позволил мне стать экспертом в области производства листового металла, механической обработки, машиностроения и станков для обработки металлов. Я постоянно думаю, читаю и пишу об этих предметах, постоянно стремясь оставаться на переднем крае своей области. Позвольте моим знаниям и опыту стать преимуществом для вашего бизнеса.
RU 
EN 
AR 
DE 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
KO