Калькулятор пособия на изгиб (онлайн и бесплатно)

Понимание пособия на изгиб

Припуск на изгиб - это фундаментальное понятие в производстве листового металла, необходимое для достижения точных размеров гнутых металлических деталей. Он учитывает удлинение материала, происходящее в процессе гибки, обеспечивая соответствие конечных размеров детали проектным спецификациям.

Определение пособия на изгиб

Припуск на изгиб - это длина нейтральной оси от начала до конца изгиба. Нейтральная ось - это воображаемая линия в материале, которая не подвергается сжатию или растяжению при изгибе. Этот расчет очень важен для определения схемы плоской детали из листового металла, так как он учитывает деформацию материала при изгибе.

Значение в проектировании листового металла

Точный расчет припусков на изгиб крайне важен по нескольким причинам. Во-первых, он гарантирует, что конечные размеры гнутой детали будут соответствовать проектным спецификациям. Кроме того, он помогает минимизировать отходы материала, точно предсказывая необходимое количество материала. Сокращение отходов приводит к экономии средств в процессе производства за счет снижения риска ошибок и переделок.

Факторы, влияющие на величину допуска на изгиб

На припуск на изгиб влияют несколько факторов. Толщина материала (T) играет важную роль, так как более толстые материалы имеют другие характеристики изгиба по сравнению с более тонкими. Угол изгиба (θ), обычно измеряемый как дополнительный угол, влияет на то, насколько сильно будет растягиваться материал. Внутренний радиус (r) изгиба на внутренней стороне материала также влияет на расчет. Наконец, решающее значение имеет коэффициент K (K) - константа, зависящая от конкретного материала и представляющая собой соотношение между толщиной материала и нейтральной осью.

Формула пособия на изгиб

Припуск на изгиб можно рассчитать по следующей формуле:

Где:

• ( BA ) - это припуск на изгиб.
• ( θ ) - угол изгиба в градусах.
• ( π/180 ) - коэффициент преобразования для перевода градусов в радианы.
• ( r ) - внутренний радиус.
• ( K ) - это коэффициент K.
• ( T ) - толщина материала.

Практический пример

Рассмотрим деталь из листового металла со следующими свойствами:

• Угол изгиба (( θ )) = 90°
• Внутренний радиус (( r )) = 5 мм
• Толщина материала (( T )) = 2 мм
• Коэффициент K (( K )) = 0,33

Используйте формулу припуска на изгиб:

Этот расчет обеспечивает припуск на изгиб, необходимый для точной разработки плоской детали из листового металла.

I. Калькулятор припусков на изгиб

Для новых листогибочный пресс Операторам, которые не знакомы с тонкостями расчета припусков на изгиб, калькулятор припусков на изгиб может стать неоценимым помощником. Этот калькулятор упрощает процесс, обеспечивая точные результаты и делая ежедневную работу более эффективной.

Онлайн-калькуляторы припусков на изгиб упрощают этот процесс, позволяя пользователям вводить такие параметры, как толщина материала, угол изгиба, внутренний радиус и коэффициент K. Затем эти калькуляторы рассчитывают припуск на изгиб, а иногда и вычет на изгиб, обеспечивая точность изготовления листового металла. Используя эти инструменты, производители могут сэкономить время и снизить риск ошибок в расчетах.

Параметры, необходимые для расчета

Чтобы эффективно использовать калькулятор припусков на изгиб, операторам необходимо ввести следующие параметры:

1. Толщина материала: Толщина материала влияет на радиус изгиба и общий припуск на изгиб.
2. Внутренний радиус: Радиус изгиба на внутренней поверхности материала.
3. К-фактор: Коэффициент, который помогает определить положение нейтральной оси при изгибе.
4. Угол изгиба: Угол, под которым сгибается материал.

Сопутствующий калькулятор:

• Калькулятор коэффициента K
• Калькулятор коэффициента Y
• Калькулятор вычетов на изгиб

Дальнейшее чтение:

• Как рассчитать припуск на изгиб, вычет на изгиб и K-фактор?

II. Что такое Допуск на изгиб?

Припуск на изгиб - это дополнительная длина материала, необходимая при гибке листового металла для достижения требуемых конечных размеров после формовки. Он компенсирует растяжение и сжатие материала в процессе гибки. Припуск на изгиб зависит от нескольких факторов:

1. Свойства материала: Различные материалы обладают различной упругостью и пластичностью, которые влияют на то, насколько сильно материал растягивается или сжимается при изгибе.
2. Толщина листа: Более толстые листы обычно требуют большего припуска на изгиб по сравнению с более тонкими листами из того же материала.
3. Метод гибки и оснастка: Тип процесса гибки (например, воздушная гибка, доводка, чеканка) и конструкция гибочного штампа могут влиять на припуск на изгиб.
4. Радиус внутреннего изгиба: Для более узкого внутреннего радиуса изгиба обычно требуется меньший припуск на изгиб, чем для большего радиуса.

Значения припусков на изгиб обычно определяются путем сочетания эмпирических данных, математических расчетов и практического опыта. Опытные конструкторы и инженеры по листовому металлу разработали таблицы и формулы припусков на изгиб за годы многократных испытаний и проверок.

Используя соответствующую формулу припуска на изгиб или обращаясь к надежным таблицам припусков на изгиб, конструкторы могут точно рассчитать размеры плоской детали из листового металла, которые позволят получить желаемые конечные размеры изгиба. Это очень важно для создания точных плоских деталей и обеспечения того, что согнутая деталь будет соответствовать и функционировать так, как задумано.

III. Формула надбавки за изгиб

Расчеты припусков на изгиб и вычетов на изгиб - важные методы, используемые для определения длины листового металла в плоском виде, обеспечивающие достижение желаемого размера гнутой детали. Понимание этих расчетов имеет решающее значение для точности изготовления листового металла.

Метод расчета припусков на изгиб:

Припуск на изгиб (BA) - это количество материала, которое добавляется к общей длине плоского листа, чтобы учесть материал, который будет использоваться при изгибе. 

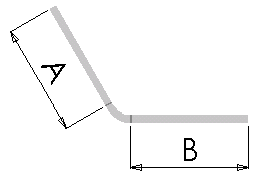
Для определения общей длины сплющивания при использовании величины припуска на изгиб используется следующее уравнение:

L_t = A + B + BA

Где:

• 𝐿_𝑡 общая длина плоскости.
• 𝐴 и 𝐵 - длины двух прямых участков металлического листа до изгиба (как показано на рисунке).
• 𝐵𝐴 - величина припуска на изгиб.

Метод расчета вычета за изгиб:

Вычет на изгиб (BD) - это количество материала, которое вычитается из общей длины плоского листа, чтобы учесть материал, который будет использоваться при изгибе. 

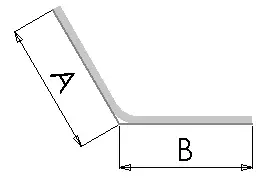
Следующее уравнение используется для определения общей длины сплющивания при использовании значения вычитания изгиба:

L_t = A + B - BD

Где:

• 𝐿_𝑡 общая длина плоскости.
• 𝐴 и 𝐵 - длины двух прямых участков металлического листа до изгиба (как показано на рисунке).
• 𝐵𝐷 - величина вычета на изгиб.

Другие методы расчета

Помимо методов припуска на изгиб и вычитания изгиба, для определения плоской длины листового металла можно использовать и другие методы. К ним относятся:

• Диаграмма допусков на изгиб: Предварительно рассчитанная диаграмма, которая содержит значения припусков на изгиб для различных материалов и углов изгиба.
• K-Factor: Коэффициент, отражающий расположение нейтральной оси относительно толщины материала. Используется для более точных расчетов на изгиб.
• Расчеты изгибов: Для получения точных результатов необходимо использовать более сложные формулы и учитывать такие параметры, как свойства материала, радиус изгиба и толщину.

IV. Диаграмма допустимых изгибов

1. Диаграмма припусков на изгиб для SPCC (низкоуглеродистая сталь)

2. Таблица припусков на изгиб для SUS (нержавеющая сталь)

3. Таблица припусков на изгиб для SPHC (нержавеющая сталь)

4. Таблица припусков на изгиб для SECC (оцинкованный стальной лист)

5. Таблица припусков на изгиб для алюминиевой пластины

V. Важность коэффициента K

Определение и роль К-фактора

Коэффициент K - это важнейший коэффициент при изготовлении листового металла, отражающий относительное положение нейтральной оси в толще материала. Нейтральная ось - это воображаемая плоскость в материале, где в процессе изгиба не происходит сжатия или растяжения. Коэффициент K рассчитывается как отношение расстояния от внутренней поверхности до нейтральной оси к общей толщине материала. Понимание коэффициента K необходимо для точных расчетов припусков на изгиб, обеспечивающих точность конечных размеров гнутых деталей.

Влияние на допуски на изгиб

Коэффициент K напрямую влияет на припуск на изгиб, который представляет собой дополнительную длину материала, необходимую для обеспечения изгиба. Формула припуска на изгиб, которая обычно включает угол изгиба, внутренний радиус, толщину материала и коэффициент K, имеет вид:

где ( BA ) - припуск на изгиб, ( θ ) - угол изгиба в радианах, ( r ) - внутренний радиус, ( K ) - коэффициент K, а ( T ) - толщина материала. Эта формула подчеркивает важность коэффициента K для обеспечения точного расчета припуска на изгиб, что очень важно для достижения точных размеров детали и сокращения отходов материала.

Зависимость от материалов и процессов

Коэффициент K не является постоянной величиной и зависит от нескольких факторов, включая свойства материала, метод изгиба, радиус изгиба и угол изгиба. Различные материалы и условия изгиба приводят к различным значениям коэффициента K, обычно в диапазоне от 0,3 до 0,5. Например, материал с высокой пластичностью может иметь другой коэффициент K по сравнению с более хрупким материалом, что влияет на припуск на изгиб и, следовательно, на конечные размеры детали.

VI. Практическое применение: Пошаговое руководство

Шаг 1: Сбор необходимых параметров

Чтобы точно рассчитать припуск на изгиб и вычет на изгиб, начните со сбора следующих параметров:

• Толщина материала (T): Измерьте толщину металлического листа, обычно в миллиметрах (мм) или дюймах (дюйм).
• Угол изгиба (θ): Определите угол, под которым будет согнут металлический лист. Обычно используются углы 90°, 120° и т. д.
• Внутренний радиус (IR): Измерьте радиус изгиба на внутренней стороне материала.
• К-фактор (К): Коэффициент K представляет собой отношение нейтральной оси материала к его толщине и необходим для определения количества материала, требуемого для изгиба. Обычно он составляет от 0,3 до 0,5, в зависимости от свойств и толщины материала.

Шаг 2: Рассчитайте допустимый изгиб (BA)

Припуск на изгиб учитывает дополнительную длину материала, необходимую для размещения изгиба. Для определения этого значения используйте формулу припуска на изгиб:

Пример расчета:

• Материал: Мягкая сталь
• Толщина (T): 0,125 дюйма
• Внутренний радиус (IR): 0,250 дюйма
• Угол изгиба (θ): 90 градусов
• К-фактор (К): 0.42

1. Переведите угол изгиба в радианы:

2. Примените формулу допуска на изгиб:

Шаг 3: Рассчитайте внешний отступ (OSSB)

Затем определите внешний отступ, который важен для расчета вычета на изгиб. Формула для OSSB выглядит следующим образом:

Пример расчета:

• Угол изгиба (θ): 90 градусов
• Толщина материала (T): 0,125 дюйма
• Внутренний радиус (IR): 0,250 дюйма

Преобразование угла изгиба в радианы:

Примените формулу внешнего отступа:

Шаг 4: Рассчитайте вычет на изгиб (BD)

Наконец, используйте внешнее отступление и припуск на изгиб, чтобы определить вычет на изгиб, который имеет решающее значение для достижения точных размеров при изготовлении листового металла:

Пример расчета:

• Внешний зазор (OSSB): 0,375 дюйма
• Припуск на изгиб (BA): 0,475 дюйма

Примените формулу вычитания изгиба:

Практические соображения

Понимание значения каждого параметра жизненно важно для успешного выполнения гибочных операций. Например, коэффициент K влияет на то, сколько материала необходимо для изгиба, а припуск на изгиб обеспечивает правильную посадку материала после гибки. Кроме того, необходимо учитывать обратную пружину - явление, при котором металл после гибки немного возвращается к своей первоначальной форме, что может привести к необходимости перегибать материал.

Выполнив эти действия и тщательно продумав каждый параметр, вы сможете точно рассчитать припуски на изгиб и вычеты на изгиб, необходимые для точного изготовления листового металла.